fbd54c7a75ad3389921cf0248c2658b2.ppt
- Количество слайдов: 32
 Chapter 14: Fluid Mechanics
Chapter 14: Fluid Mechanics
 COURSE THEME: NEWTON’S LAWS OF MOTION! • Chs. 5 - 13: Methods to analyze dynamics of objects in Translational & Rotational Motion using Newton’s Laws! Chs. 5 & 6: Newton’s Laws using Forces (translational motion) Chs. 7 & 8: Newton’s Laws using Energy & Work (translational motion) Ch. 9: Newton’s Laws using Momentum (translational motion) Chs. 10 & 11: Newton’s Laws (rotational language; rotating objects). NOW • Ch. 14: Methods to analyze the dynamics of fluids in motion. First, we need to discuss FLUID LANGUAGE. Then, Newton’s Laws in Fluid Language!
COURSE THEME: NEWTON’S LAWS OF MOTION! • Chs. 5 - 13: Methods to analyze dynamics of objects in Translational & Rotational Motion using Newton’s Laws! Chs. 5 & 6: Newton’s Laws using Forces (translational motion) Chs. 7 & 8: Newton’s Laws using Energy & Work (translational motion) Ch. 9: Newton’s Laws using Momentum (translational motion) Chs. 10 & 11: Newton’s Laws (rotational language; rotating objects). NOW • Ch. 14: Methods to analyze the dynamics of fluids in motion. First, we need to discuss FLUID LANGUAGE. Then, Newton’s Laws in Fluid Language!
 Fluid Mechanics • The three (common) states or phases of matter are: 1. Solid: Has a definite volume & shape. Maintains it’s shape & size (approximately), even under large forces. 2. Liquid: Has a definite volume, but not a definite shape. It takes the shape of it’s container. 3. Gas: Has neither a definite volume nor a definite shape. It expands to fill it’s container. NOTE! These definitions are somewhat artificial – The time it takes a substance to change its shape in response to an external force determines whether the substance is a solid, liquid or gas Chapter 14 lumps 2. & 3. into the category of FLUIDS
Fluid Mechanics • The three (common) states or phases of matter are: 1. Solid: Has a definite volume & shape. Maintains it’s shape & size (approximately), even under large forces. 2. Liquid: Has a definite volume, but not a definite shape. It takes the shape of it’s container. 3. Gas: Has neither a definite volume nor a definite shape. It expands to fill it’s container. NOTE! These definitions are somewhat artificial – The time it takes a substance to change its shape in response to an external force determines whether the substance is a solid, liquid or gas Chapter 14 lumps 2. & 3. into the category of FLUIDS
 Fluids • Fluids: Have the ability to flow. • A fluid is a collection of molecules that are randomly arranged & held together by weak cohesive forces & by forces exerted by the walls of a container. Both liquids & gases are fluids
Fluids • Fluids: Have the ability to flow. • A fluid is a collection of molecules that are randomly arranged & held together by weak cohesive forces & by forces exerted by the walls of a container. Both liquids & gases are fluids
 Fluid Mechanics • Two basic categories of fluid mechanics: • Fluid Statics – Obviously, describes fluids at rest • Fluid Dynamics – Obviously, describes fluids in motion • The same physical principles (Newton’s Laws) that have applied in our studies up to now will also apply to fluids. But, first, we need to introduce Fluid Language.
Fluid Mechanics • Two basic categories of fluid mechanics: • Fluid Statics – Obviously, describes fluids at rest • Fluid Dynamics – Obviously, describes fluids in motion • The same physical principles (Newton’s Laws) that have applied in our studies up to now will also apply to fluids. But, first, we need to introduce Fluid Language.
 Density & Specific Gravity Not discussed much in your text! Plays the role for fluids that mass plays for solid objects • Density, ρ (lower case Greek rho, NOT p!) of object, mass M & volume V: ρ (M/V) (kg/m 3 = 10 -3 g/cm 3) • Specific Gravity (SG): Ratio of density of a substance to density of water. ρwater = 1 g/cm 3 = 1000 kg/m 3 See table!!
Density & Specific Gravity Not discussed much in your text! Plays the role for fluids that mass plays for solid objects • Density, ρ (lower case Greek rho, NOT p!) of object, mass M & volume V: ρ (M/V) (kg/m 3 = 10 -3 g/cm 3) • Specific Gravity (SG): Ratio of density of a substance to density of water. ρwater = 1 g/cm 3 = 1000 kg/m 3 See table!!
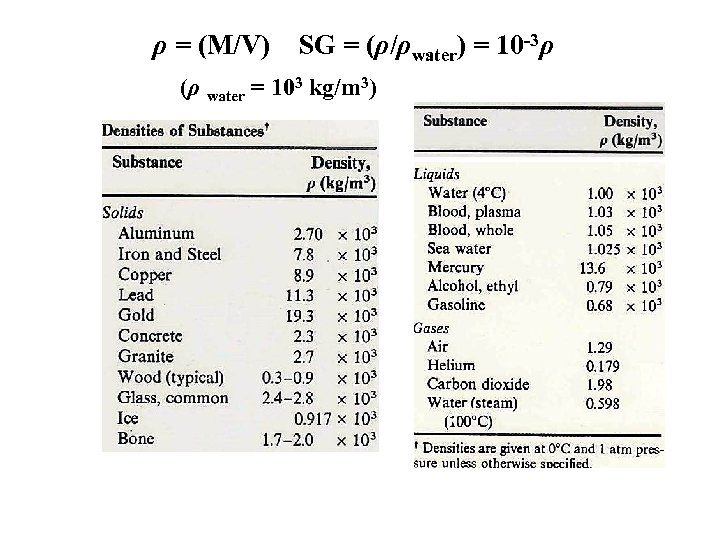 ρ = (M/V) SG = (ρ/ρwater) = 10 -3ρ (ρ water = 103 kg/m 3)
ρ = (M/V) SG = (ρ/ρwater) = 10 -3ρ (ρ water = 103 kg/m 3)
 NOTE: 1. The density for a substance varies slightly with temperature, since volume is temperature dependent 2. The values of densities for various substances are an indication of the average molecular spacing in the substance. They show that this spacing is much greater than it is in a solid or liquid
NOTE: 1. The density for a substance varies slightly with temperature, since volume is temperature dependent 2. The values of densities for various substances are an indication of the average molecular spacing in the substance. They show that this spacing is much greater than it is in a solid or liquid
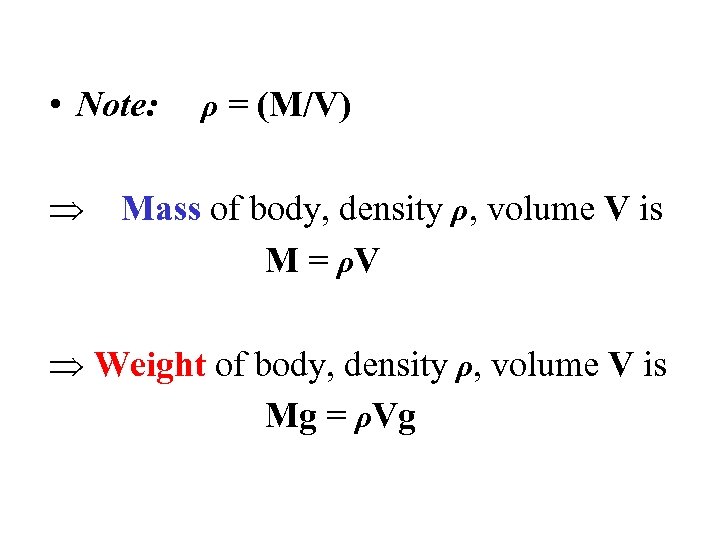 • Note: ρ = (M/V) Mass of body, density ρ, volume V is M = ρV Weight of body, density ρ, volume V is Mg = ρVg
• Note: ρ = (M/V) Mass of body, density ρ, volume V is M = ρV Weight of body, density ρ, volume V is Mg = ρVg
 Forces in Fluids • To do fluid dynamics using Newton’s Laws, we obviously need to talk about forces in fluids. • Unlike solids: – Static Fluids do not sustain shearing forces (stresses). Shearing forces are exerted parallel to fluid surfaces. – Static Fluids do not sustain tensile forces (stresses). Tensile forces are exerted perpendicular to the fluid surface. • The only force that can be exerted on an object submerged in a Static Fluid is one that tends to compress the object from all sides • The force exerted by a Static Fluid on an object is always perpendicular to the surfaces of the object
Forces in Fluids • To do fluid dynamics using Newton’s Laws, we obviously need to talk about forces in fluids. • Unlike solids: – Static Fluids do not sustain shearing forces (stresses). Shearing forces are exerted parallel to fluid surfaces. – Static Fluids do not sustain tensile forces (stresses). Tensile forces are exerted perpendicular to the fluid surface. • The only force that can be exerted on an object submerged in a Static Fluid is one that tends to compress the object from all sides • The force exerted by a Static Fluid on an object is always perpendicular to the surfaces of the object
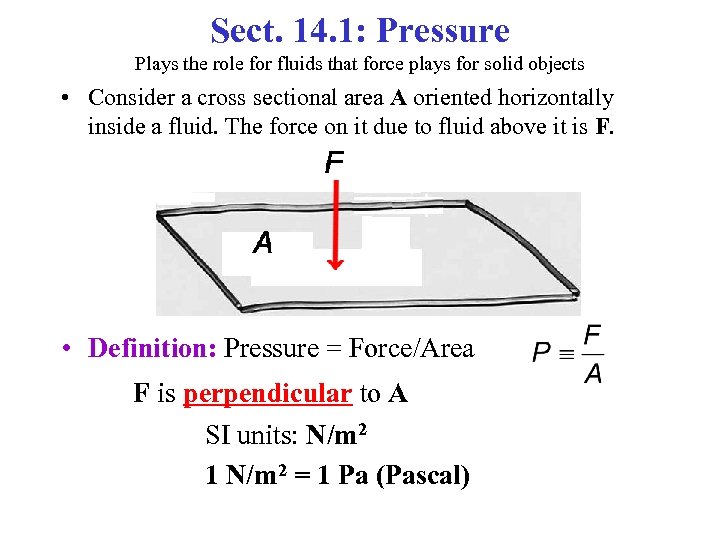 Sect. 14. 1: Pressure Plays the role for fluids that force plays for solid objects • Consider a cross sectional area A oriented horizontally inside a fluid. The force on it due to fluid above it is F. • Definition: Pressure = Force/Area F is perpendicular to A SI units: N/m 2 1 N/m 2 = 1 Pa (Pascal)
Sect. 14. 1: Pressure Plays the role for fluids that force plays for solid objects • Consider a cross sectional area A oriented horizontally inside a fluid. The force on it due to fluid above it is F. • Definition: Pressure = Force/Area F is perpendicular to A SI units: N/m 2 1 N/m 2 = 1 Pa (Pascal)
 • Consider a solid object submerged in a STATIC fluid as in the figure. • The pressure P of the fluid at the level to which the object has been submerged is the ratio of the force (due to the fluid surrounding it in all directions) to the area • At a particular point, P has the following properties: 1. It is same in all directions. 2. It is to any surface of the object. If 1. & 2. weren’t true, the fluid would be in motion, violating the statement that it is static!
• Consider a solid object submerged in a STATIC fluid as in the figure. • The pressure P of the fluid at the level to which the object has been submerged is the ratio of the force (due to the fluid surrounding it in all directions) to the area • At a particular point, P has the following properties: 1. It is same in all directions. 2. It is to any surface of the object. If 1. & 2. weren’t true, the fluid would be in motion, violating the statement that it is static!
 • P is any fluid solid surface: P = (F /A)
• P is any fluid solid surface: P = (F /A)
 • Note that pressure is a scalar, in contrast with force, which is a vector. It is proportional to the magnitude of the force • Suppose the pressure varies over an area. Consider a differential area d. A. That area has a force d. F on it and d. F = P d. A • The direction of the force producing a pressure is perpendicular to the area of interest.
• Note that pressure is a scalar, in contrast with force, which is a vector. It is proportional to the magnitude of the force • Suppose the pressure varies over an area. Consider a differential area d. A. That area has a force d. F on it and d. F = P d. A • The direction of the force producing a pressure is perpendicular to the area of interest.
 Pressure Measurements • A possible means of measuring the pressure in a fluid is to submerge a measuring device in the fluid. • A common device is shown in the lower figure. It is an evacuated cylinder with a piston connected to an ideal spring. It is first calibrated with a known force. • After it is submerged, the force due to the fluid presses on the top of the piston & compresses the spring. • The force the fluid exerts on the piston is then measured. Knowing the area A, the pressure can then be found.
Pressure Measurements • A possible means of measuring the pressure in a fluid is to submerge a measuring device in the fluid. • A common device is shown in the lower figure. It is an evacuated cylinder with a piston connected to an ideal spring. It is first calibrated with a known force. • After it is submerged, the force due to the fluid presses on the top of the piston & compresses the spring. • The force the fluid exerts on the piston is then measured. Knowing the area A, the pressure can then be found.
 Sect. 14. 2: Variation of Pressure with Depth • Experimental Fact: Pressure depends on depth. • See figure. If a static fluid is in a container, all portions of the fluid must be in static equilibrium. • All points at the same depth must be at the same pressure – Otherwise, the fluid would not be static. • Consider the darker region, which is a sample of liquid with a cylindrical shape – It has a cross-sectional area A – Extends from depth d to d + h below the surface • The liquid has a density r – Assume the density is the same throughout the fluid – This means it is an incompressible liquid
Sect. 14. 2: Variation of Pressure with Depth • Experimental Fact: Pressure depends on depth. • See figure. If a static fluid is in a container, all portions of the fluid must be in static equilibrium. • All points at the same depth must be at the same pressure – Otherwise, the fluid would not be static. • Consider the darker region, which is a sample of liquid with a cylindrical shape – It has a cross-sectional area A – Extends from depth d to d + h below the surface • The liquid has a density r – Assume the density is the same throughout the fluid – This means it is an incompressible liquid
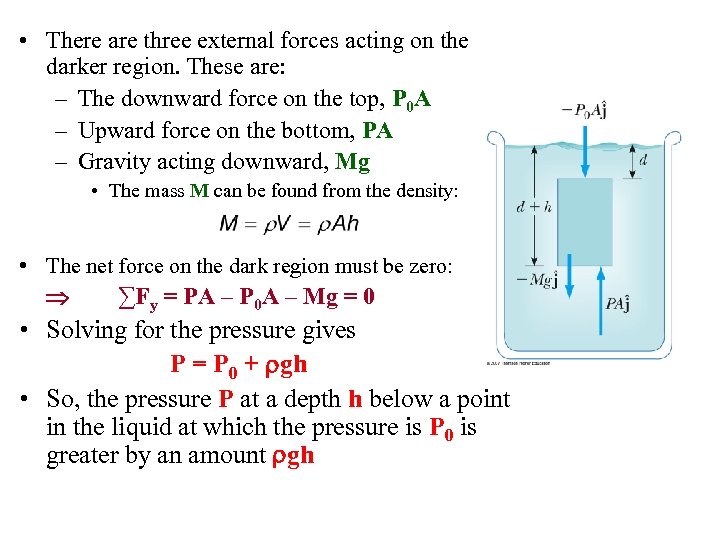 • There are three external forces acting on the darker region. These are: – The downward force on the top, P 0 A – Upward force on the bottom, PA – Gravity acting downward, Mg • The mass M can be found from the density: • The net force on the dark region must be zero: ∑Fy = PA – P 0 A – Mg = 0 • Solving for the pressure gives P = P 0 + rgh • So, the pressure P at a depth h below a point in the liquid at which the pressure is P 0 is greater by an amount rgh
• There are three external forces acting on the darker region. These are: – The downward force on the top, P 0 A – Upward force on the bottom, PA – Gravity acting downward, Mg • The mass M can be found from the density: • The net force on the dark region must be zero: ∑Fy = PA – P 0 A – Mg = 0 • Solving for the pressure gives P = P 0 + rgh • So, the pressure P at a depth h below a point in the liquid at which the pressure is P 0 is greater by an amount rgh
 • At depth h below surface of liquid: Change in pressure with change in depth: P = ρg h (for a fluid at rest only!) P = P 2 -P 1 = ρg(h 2 -h 1) ρg h
• At depth h below surface of liquid: Change in pressure with change in depth: P = ρg h (for a fluid at rest only!) P = P 2 -P 1 = ρg(h 2 -h 1) ρg h
 Example
Example
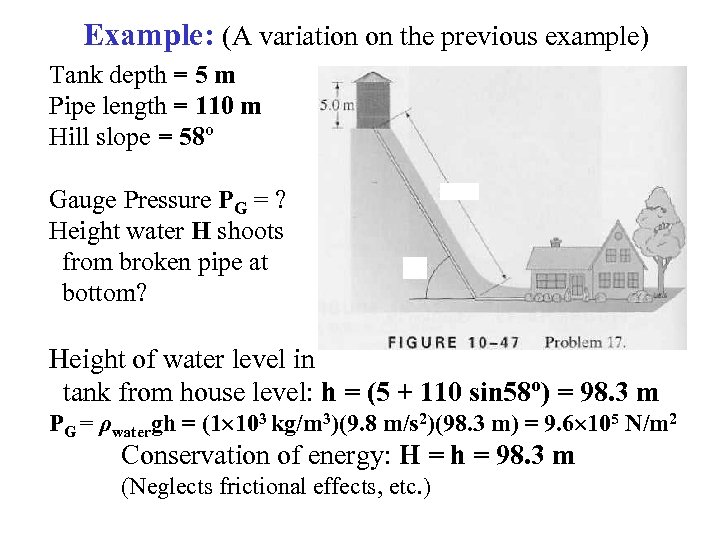 Example: (A variation on the previous example) Tank depth = 5 m Pipe length = 110 m Hill slope = 58º Gauge Pressure PG = ? Height water H shoots from broken pipe at bottom? Height of water level in tank from house level: h = (5 + 110 sin 58º) = 98. 3 m PG = ρwatergh = (1 103 kg/m 3)(9. 8 m/s 2)(98. 3 m) = 9. 6 105 N/m 2 Conservation of energy: H = h = 98. 3 m (Neglects frictional effects, etc. )
Example: (A variation on the previous example) Tank depth = 5 m Pipe length = 110 m Hill slope = 58º Gauge Pressure PG = ? Height water H shoots from broken pipe at bottom? Height of water level in tank from house level: h = (5 + 110 sin 58º) = 98. 3 m PG = ρwatergh = (1 103 kg/m 3)(9. 8 m/s 2)(98. 3 m) = 9. 6 105 N/m 2 Conservation of energy: H = h = 98. 3 m (Neglects frictional effects, etc. )
 Atmospheric Pressure • Earth’s atmosphere: A fluid. – But doesn’t have a fixed top “surface”! • Change in height h above Earth’s surface: Change in pressure: P = ρg h • Sea level: P 0 1. 013 105 N/m 2 = 101. 3 k. Pa 1 atm – Old units: 1 bar = 1. 00 105 N/m 2 • Physics: Cause of pressure at any height: Weight of air above that height!
Atmospheric Pressure • Earth’s atmosphere: A fluid. – But doesn’t have a fixed top “surface”! • Change in height h above Earth’s surface: Change in pressure: P = ρg h • Sea level: P 0 1. 013 105 N/m 2 = 101. 3 k. Pa 1 atm – Old units: 1 bar = 1. 00 105 N/m 2 • Physics: Cause of pressure at any height: Weight of air above that height!
 Gauge Pressure • Pressure gauges (like tire gauges, etc. ) measure difference between atmospheric pressure P 0 & internal pressure (of tire, for example). • Gauge pressure: PG = P – P 0
Gauge Pressure • Pressure gauges (like tire gauges, etc. ) measure difference between atmospheric pressure P 0 & internal pressure (of tire, for example). • Gauge pressure: PG = P – P 0
 Conceptual Example P=? Pressure on A: Pdown = P + Pmg Pup = PA At rest ∑Fy = 0 Pup = Pdown or PA = P + Pmg P = PA - Pmg < PA So, air pressure holds fluid in straw!
Conceptual Example P=? Pressure on A: Pdown = P + Pmg Pup = PA At rest ∑Fy = 0 Pup = Pdown or PA = P + Pmg P = PA - Pmg < PA So, air pressure holds fluid in straw!
 Pascal’s Law • Experimental fact: An external pressure P applied to confined fluid increases the pressure throughout a fluid by P Pascal’s Principle • Simple example: Water in a lake (at rest). At depth h below surface, pressure is P = P 0 + ρgh (P 0 = atmospheric pressure)
Pascal’s Law • Experimental fact: An external pressure P applied to confined fluid increases the pressure throughout a fluid by P Pascal’s Principle • Simple example: Water in a lake (at rest). At depth h below surface, pressure is P = P 0 + ρgh (P 0 = atmospheric pressure)
 Pascal’s Law • Named for French scientist Blaise Pascal • A change in the pressure applied to a fluid is transmitted undiminished to every point of the fluid and to the walls of the container
Pascal’s Law • Named for French scientist Blaise Pascal • A change in the pressure applied to a fluid is transmitted undiminished to every point of the fluid and to the walls of the container
 Pascal’s Law, Example 14. 2 • Car lift in a service station. See figure. A large output force can be applied by means of a small input force. Volume of liquid pushed down on left must equal volume pushed up on right. • Circular cross section system. On left r 1 = 5 cm = 0. 05 m. On right r 2 = 15 cm = 0. 15 m. Car’s weight mg = 13, 300 N. N’s 2 nd Law on right: ∑Fy = 0 = F 2 – mg. Or F 2 = 13, 300 N Calculate minimum F 1 to lift the car & pressure P in the system. Gives Pascal’s Law F 1 = (A 1/A 2)F 2 = 14, 800 N P = (F 1/A 1) = 1. 88 105 Pa
Pascal’s Law, Example 14. 2 • Car lift in a service station. See figure. A large output force can be applied by means of a small input force. Volume of liquid pushed down on left must equal volume pushed up on right. • Circular cross section system. On left r 1 = 5 cm = 0. 05 m. On right r 2 = 15 cm = 0. 15 m. Car’s weight mg = 13, 300 N. N’s 2 nd Law on right: ∑Fy = 0 = F 2 – mg. Or F 2 = 13, 300 N Calculate minimum F 1 to lift the car & pressure P in the system. Gives Pascal’s Law F 1 = (A 1/A 2)F 2 = 14, 800 N P = (F 1/A 1) = 1. 88 105 Pa
 Example 14. 2, more analysis • The volume of liquid pushed down on left must equal volume pushed up on right. So, • Combining this with • Gives This means that Work 1 = Work 2 So, Pascal’s Law is consequence of Conservation of Mechanical Energy
Example 14. 2, more analysis • The volume of liquid pushed down on left must equal volume pushed up on right. So, • Combining this with • Gives This means that Work 1 = Work 2 So, Pascal’s Law is consequence of Conservation of Mechanical Energy
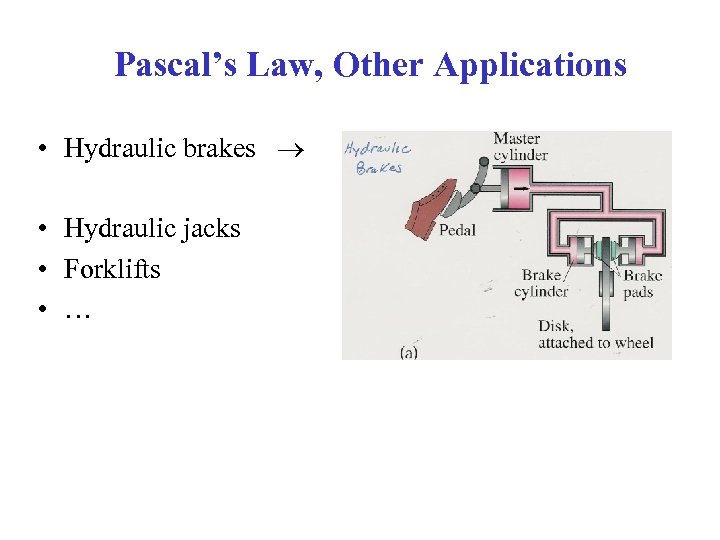 Pascal’s Law, Other Applications • Hydraulic brakes • Hydraulic jacks • Forklifts • …
Pascal’s Law, Other Applications • Hydraulic brakes • Hydraulic jacks • Forklifts • …
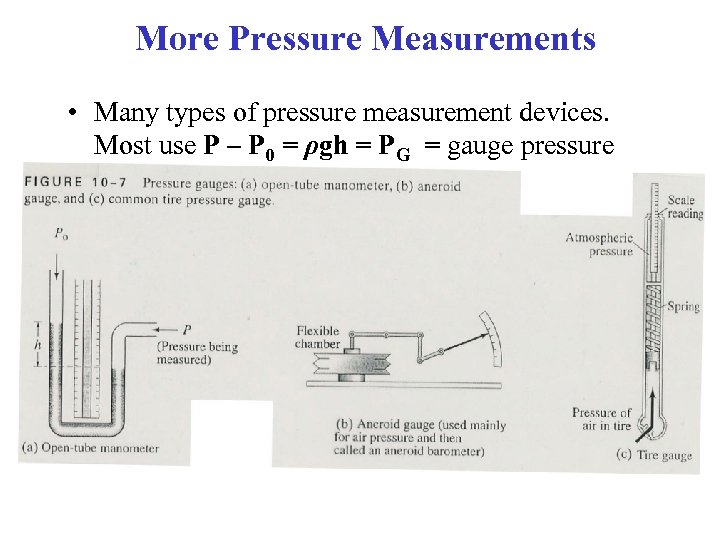 More Pressure Measurements • Many types of pressure measurement devices. Most use P – P 0 = ρgh = PG = gauge pressure
More Pressure Measurements • Many types of pressure measurement devices. Most use P – P 0 = ρgh = PG = gauge pressure
 Various Pressure Units • Gauge Pressure: P 0 = ρgh Alternate unit of pressure: Instead of calculating ρgh, common to use standard liquid (mercury, Hg or alcohol, where ρ is standard) & measure h Quote pressure in length units! For example: “millimeters of mercury” mm Hg For h = 1 mm Hg = 10 -3 m Hg ρmercury gh = (1. 36 104 kg/m 3) (9. 8 m/s 2)(10 -3 m) = 133 N/m 2 = 133 Pa 1 Torr (another pressure unit!) mm Hg & Torr are not proper SI pressure units!
Various Pressure Units • Gauge Pressure: P 0 = ρgh Alternate unit of pressure: Instead of calculating ρgh, common to use standard liquid (mercury, Hg or alcohol, where ρ is standard) & measure h Quote pressure in length units! For example: “millimeters of mercury” mm Hg For h = 1 mm Hg = 10 -3 m Hg ρmercury gh = (1. 36 104 kg/m 3) (9. 8 m/s 2)(10 -3 m) = 133 N/m 2 = 133 Pa 1 Torr (another pressure unit!) mm Hg & Torr are not proper SI pressure units!
 • About as many pressure units as there are measurement devices!! • Preferred (SI) unit: 1 Pa (Pascal) = 1 N/m 2
• About as many pressure units as there are measurement devices!! • Preferred (SI) unit: 1 Pa (Pascal) = 1 N/m 2
 Mercury Barometer • Weather reports: Barometric pressure (atmospheric pressure): 28 -32 inches Hg 76 cm = 760 mm = 29. 29 inches When h = 760 mm, P = ρmercury gh = 1. 013 105 N/m 2 = 1 atm • If use water P = 1 atm = ρwater gh h 10 m 30 feet!
Mercury Barometer • Weather reports: Barometric pressure (atmospheric pressure): 28 -32 inches Hg 76 cm = 760 mm = 29. 29 inches When h = 760 mm, P = ρmercury gh = 1. 013 105 N/m 2 = 1 atm • If use water P = 1 atm = ρwater gh h 10 m 30 feet!


