Chapter 14 A construction superintendent explained to his

Chapter 14 A construction superintendent explained to his client the massive cost overruns. He told of concrete trucks arriving too soon and having to dump their loads; of having to re-pour the foundation because the gravel underlay had not been set; of having to cut many holes through the concrete floor pad because the pipes had been covered before being inspected. Everything happened as scheduled, the poor man lamented. “You should have used PERT, ” the client admonished. 1 Project Planning with PERT and CPM

The Importance of Time in Planning § Projects may have uncertainty. § Projects may take a long time. § Activities must be scheduled. 2

Basic Concepts of PERT § PERT has an activity orientation. An activity is an effort that consumes time and resources. § The central focus of all analysis and procedures is the PERT Network. § PERT ties together all project activities as predecessors and successors. § Events are project milestones and serve as the logical glue (network nodes) for connecting activities (network arcs). 3

Project Activities in Constructing a House 4

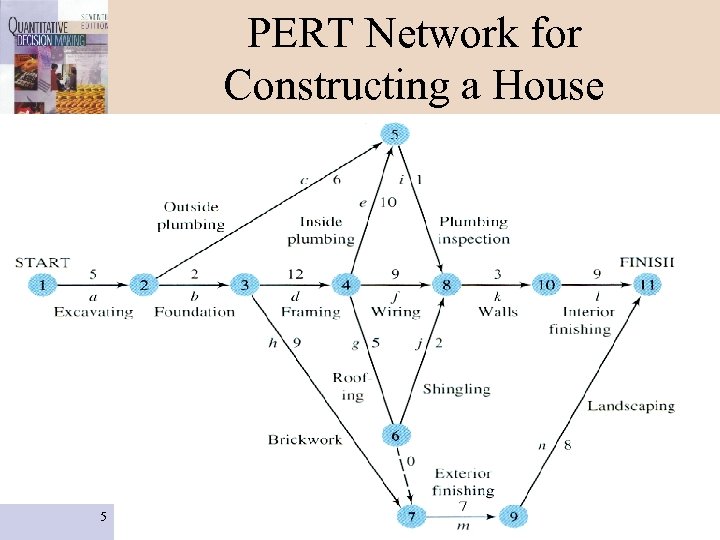PERT Network for Constructing a House 5

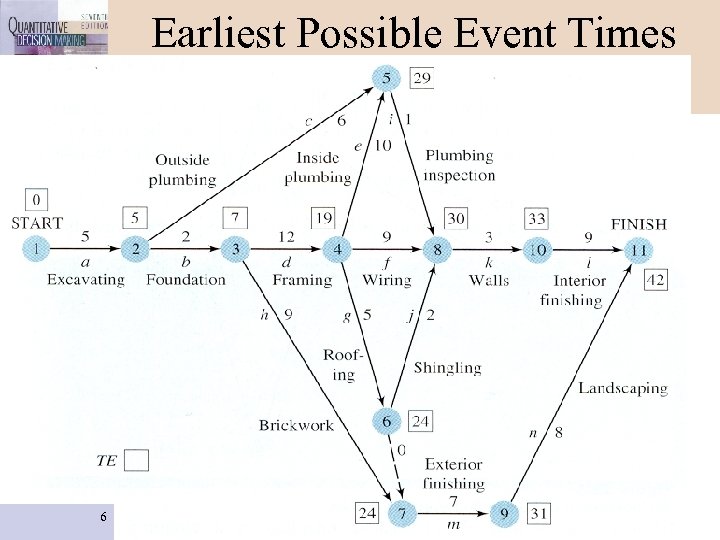Earliest Possible Event Times (TE) 6

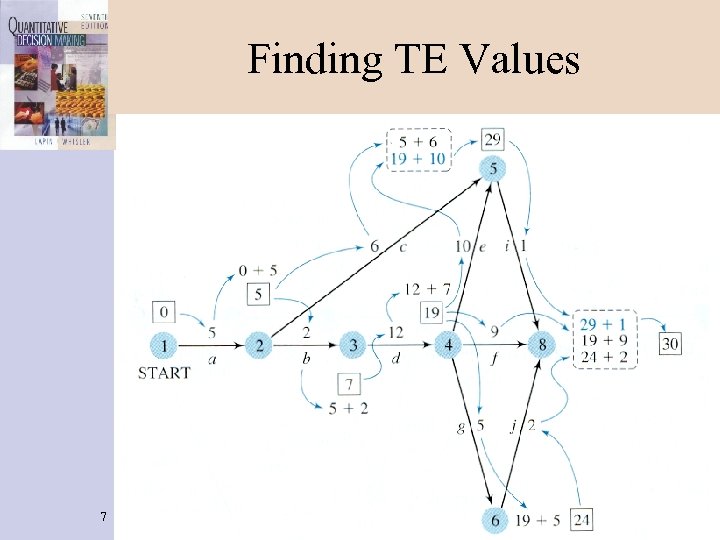Finding TE Values 7

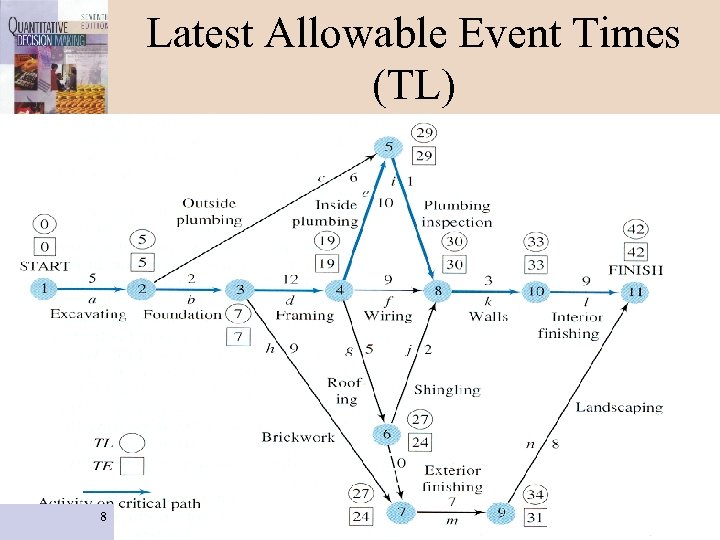Latest Allowable Event Times (TL) 8

9

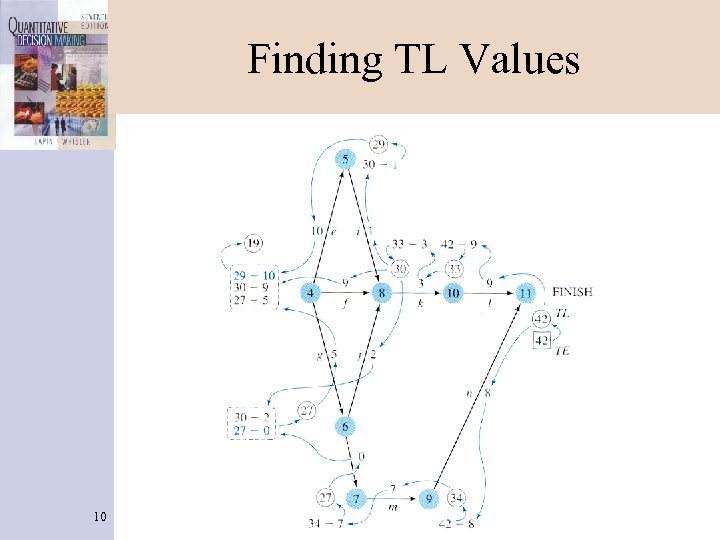Finding TL Values 10

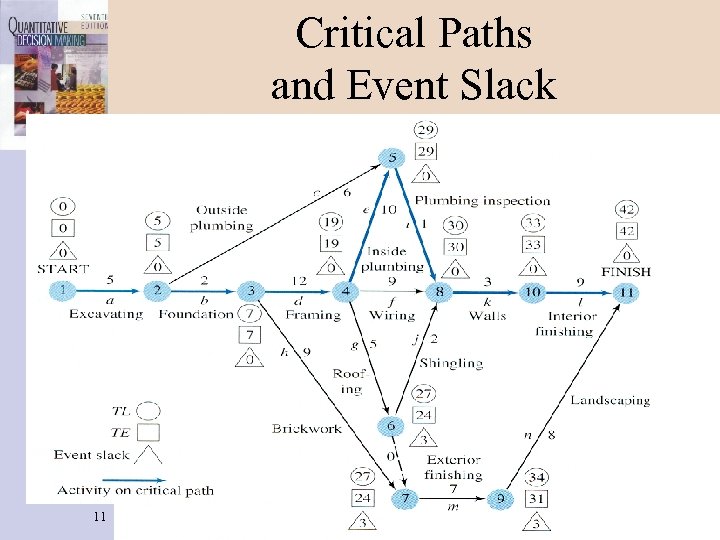Critical Paths and Event Slack 11

Activity Scheduling § Project activities need two scheduled times: the starting time and the finishing time. § PERT finds early and late values for each. § All are relative to time 0 for the project start. § An activity’s early starting time equals the TE of its beginning event: ES = TE. § An activity’s late finishing time equals the TL for its ending event: LF = TL. § From those, 2 times are computed using the expected activity completion time t: Early finishing time: EF = ES + t. 12 Late starting time: LS = LF - t.

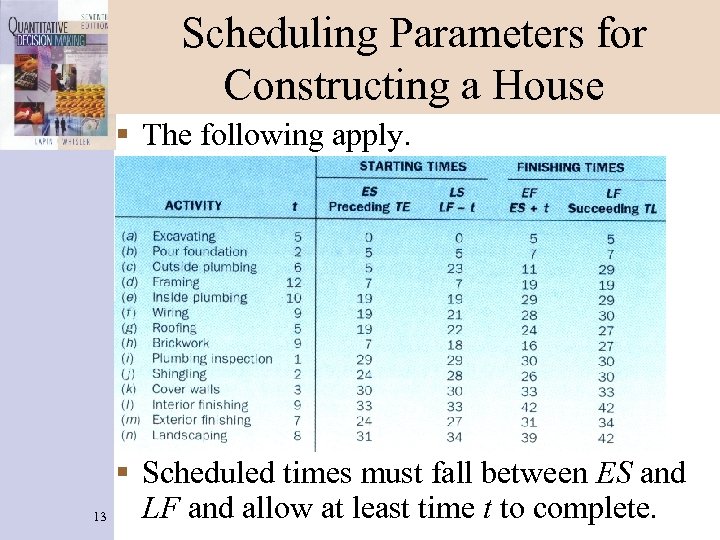Scheduling Parameters for Constructing a House § The following apply. § Scheduled times must fall between ES and LF and allow at least time t to complete. 13

Activity Slack § The activity slack expresses the scheduling leeway for the activity. It is computed by: activity slack = LS - ES = LF - EF § Critical activities have zero slack. These lie on a critical path. § Event slack and activity slack measure different things and are only loosely related. 14

Using Quick. Quant with PERT § Quick. Quant will construct a PERT network and evaluate it using only tabular data input. 15

Time Cost Tradeoffs § It is possible to speed up a project by crashing some activities at extra cost. The following data apply. 16 § To reduce project time, speed up one or more activities on the critical path.

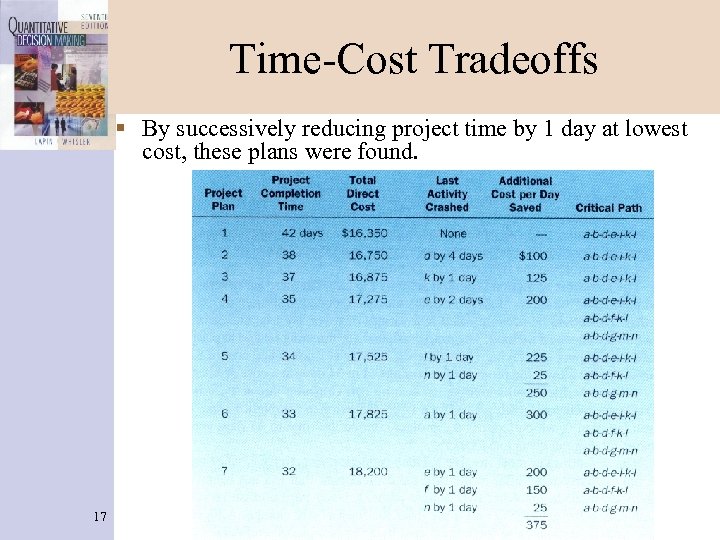Time-Cost Tradeoffs § By successively reducing project time by 1 day at lowest cost, these plans were found. 17

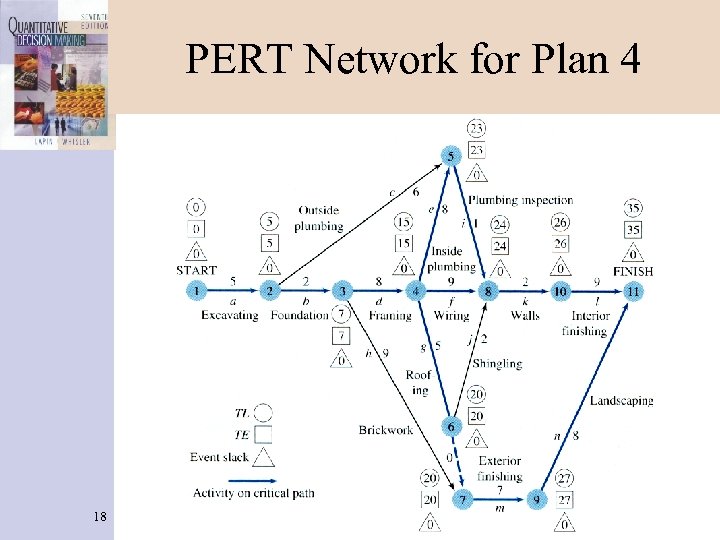PERT Network for Plan 4 18

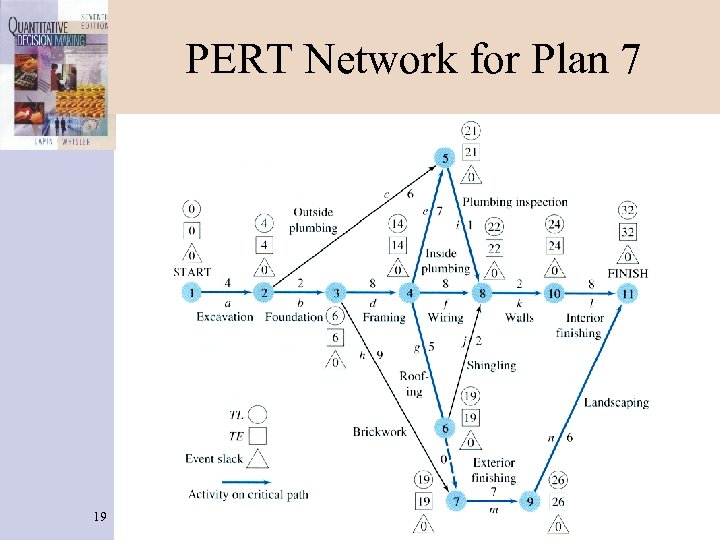PERT Network for Plan 7 19

Probabilistic Analysis § The activity completion times are really random variables and probabilities apply. § They are well represented by the modified beta distribution. § There are three time parameters: most likely m optimistic a pessimistic b § The expected value or mean and variance are computed from: a + 4 m + b t = 6 20 s 2 (b - a)2 = 62

Single Path Probabilities § The normal distribution represents probabilities for the duration T of a single path. § Using the above, the mean and variance are computed. From them, probabilities may be found that T lies in any specified interval. § Probabilities for the duration of the a priori critical path can be computed. § WARNING: That will not represent the duration of the project itself. The m computed above understates expected project duration. 21

Probabilities for Time to Construct a House § The following data apply. 22

Probabilities for Time to Construct a House § The expected duration of the critical path a-b-d-e-i-k-l is: m = 5 + 2 + 10 + 1 + 3 + 9 = 42 days § The variance for duration of that path is s 2 =. 444+7. 111+1. 000+0+. 250+. 444 = 9. 693 and the standard deviation is the square root of the above s = 3. 11 days § Using 40 days, z = (40 – 42)/3. 11 = -. 64 and Pr[T > 40] =. 5 +. 2389 =. 7389 This applies to the critical path, not to the 23 project itself.

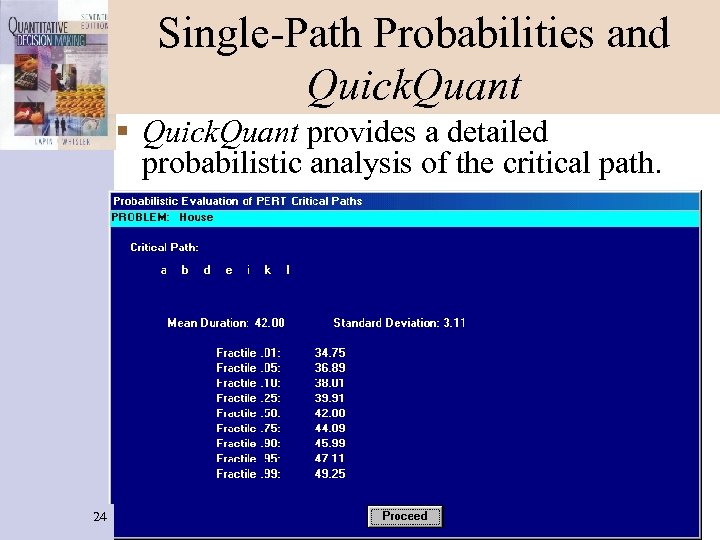Single-Path Probabilities and Quick. Quant § Quick. Quant provides a detailed probabilistic analysis of the critical path. 24

What’s Wrong with Single-Path Probabilities? § Single path probabilities do not properly apply to the project itself because many paths might end up to be the longest. § The critical path is one of many possibilities. § Durations of all these paths are not independent random variables. § To properly assess likelihoods for project duration, build the house (on paper) many times and see what happens. § Quick. Quant will do that. The procedure is called Monte Carlo simulation. 25

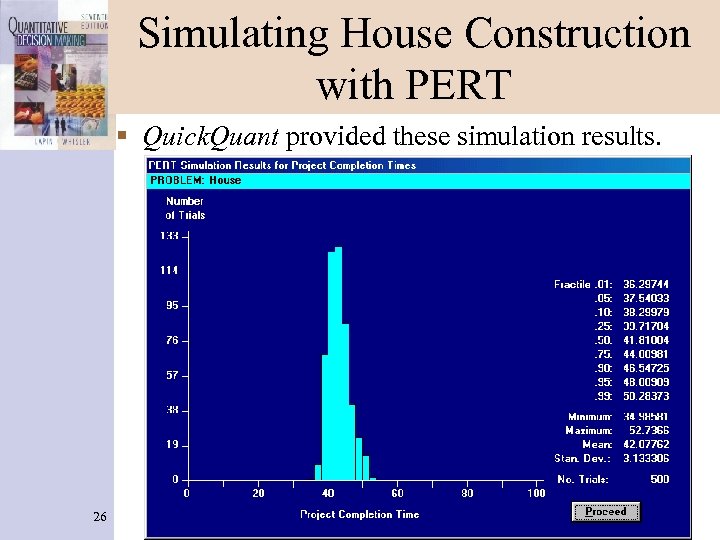Simulating House Construction with PERT § Quick. Quant provided these simulation results. 26

Simulating House Construction with PERT § The second Quick. Quant screen tells us about unexpected longest paths. § The a priori critical path was of longest duration only 437 times out of 500. In some projects, it 27 may be longest as little as 1% of the time, or less.

PERT/CPM Evaluation for Home Construction Example (Figure 14 -26) The activities on the critical path are given in column R (indicated by the word Yes). In this case they are a, b, d, e, I, k, and l. The length of the critical path is in cell N 26. It is 42 in this example. The earliest event times are given in cells C 25: M 26 28

1. Enter the problem name in cell B 3. PERT/CPM Evaluation for Home Construction Example (Figure 14 -26) 3. Enter data in the activity-event table. Put a -1 in the column where the activity starts and a +1 where the activity ends. All other entries in the row are blank. For example, cell C 8 has a -1 because activity A starts with event 1 and cell D 8 has a +1 because activity A ends with event 2. Expand the table to accommodate the proper number of activities and events by inserting or deleting rows and columns. If rows are inserted, make 29 sure to copy the formulas in columns O, P, Q, and R into these new rows.

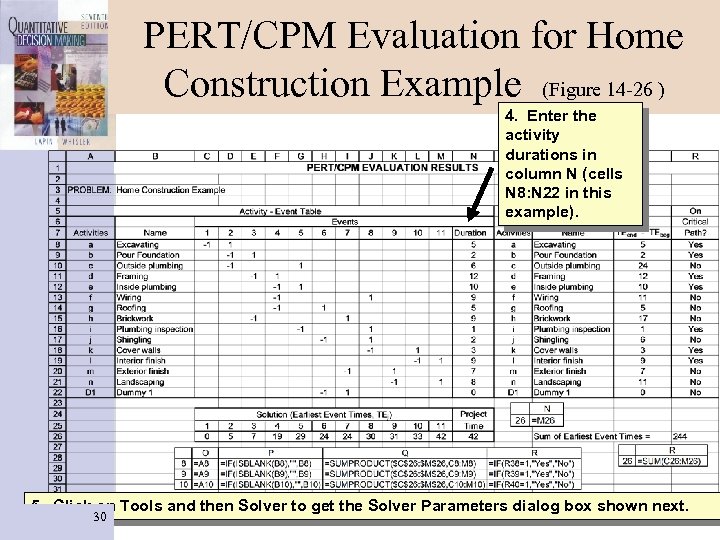PERT/CPM Evaluation for Home Construction Example (Figure 14 -26 ) 4. Enter the activity durations in column N (cells N 8: N 22 in this example). 5. Click on Tools and then Solver to get the Solver Parameters dialog box shown next. 30

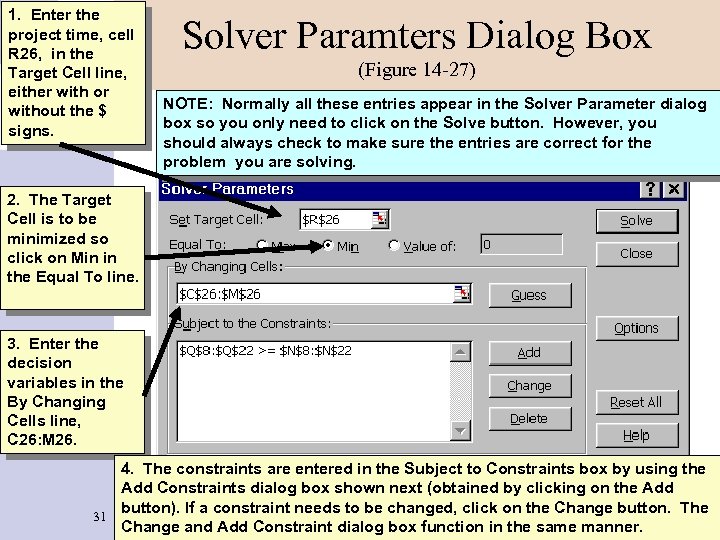1. Enter the project time, cell R 26, in the Target Cell line, either with or without the $ signs. Solver Paramters Dialog Box (Figure 14 -27) NOTE: Normally all these entries appear in the Solver Parameter dialog box so you only need to click on the Solve button. However, you should always check to make sure the entries are correct for the problem you are solving. 2. The Target Cell is to be minimized so click on Min in the Equal To line. 3. Enter the decision variables in the By Changing Cells line, C 26: M 26. 4. The constraints are entered in the Subject to Constraints box by using the Add Constraints dialog box shown next (obtained by clicking on the Add button). If a constraint needs to be changed, click on the Change button. The 31 Change and Add Constraint dialog box function in the same manner.

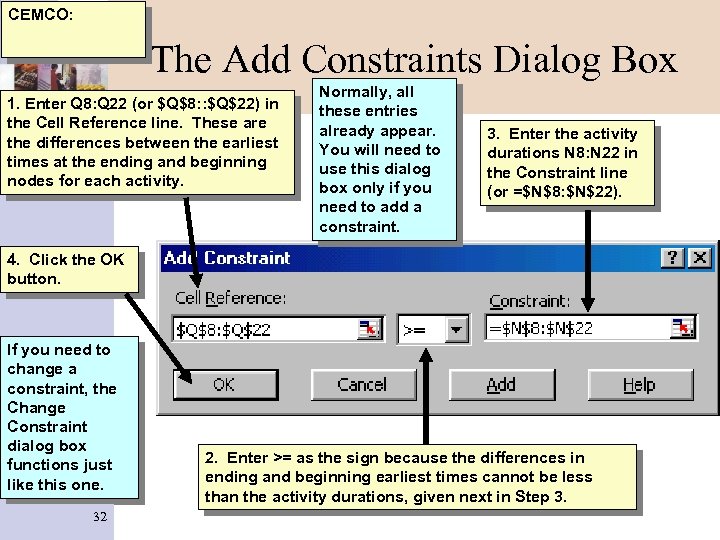CEMCO: The Add Constraints Dialog Box 1. Enter Q 8: Q 22 (or $Q$8: : $Q$22) in the Cell Reference line. These are the differences between the earliest times at the ending and beginning nodes for each activity. Normally, all these entries already appear. You will need to use this dialog box only if you need to add a constraint. 3. Enter the activity durations N 8: N 22 in the Constraint line (or =$N$8: $N$22). 4. Click the OK button. If you need to change a constraint, the Change Constraint dialog box functions just like this one. 32 2. Enter >= as the sign because the differences in ending and beginning earliest times cannot be less than the activity durations, given next in Step 3.

PERT/CPM Evaluation for Home Construction Example (Figure 14 -26) 6. To find which activities are on the critical path (in column R) copy the portion of the Sensitivity Report titled "Constraints" and paste it into this spreadsheet so that the word Constraints is in cell N 35 (for this example), as shown next. 7. If all the earliest event times are desired, run Solver once more using the sum of the 33 earliest event times (cell R 26) as the target cell.

Solver’s Sensitivity Report To get Solver’s Sensitivity Report, highlight Sensitivity Report in the Report box of the Solver Results dialog box before clicking the OK button. 34

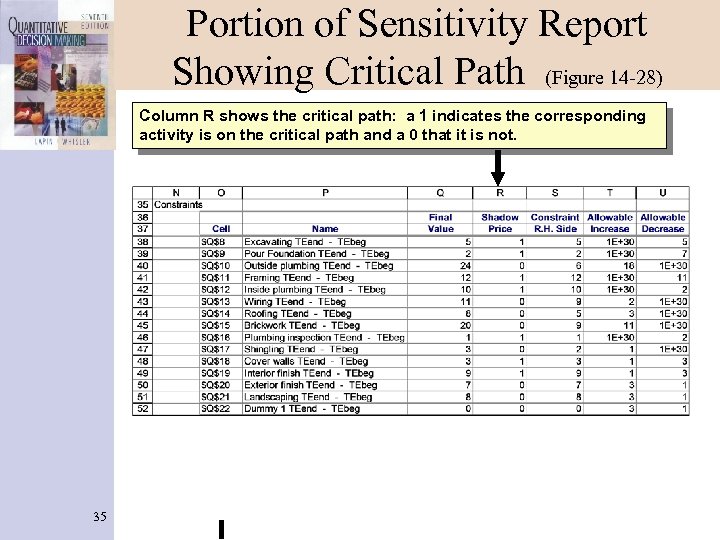Portion of Sensitivity Report Showing Critical Path (Figure 14 -28) Column R shows the critical path: a 1 indicates the corresponding activity is on the critical path and a 0 that it is not. 35