Chapter 13 Work and Energy Work Power

Chapter 13 Work and Energy

Work, Power, and Machines • Work: – Is done only when force is applied to an object and the object moves in the same direction as the applied force – Is calculated by multiplying the force by the distance over which the force is applied – Work = force x distance – W = F x d – Work is 0 when an object is not moving

Work, Power, and Machines • Work is measured in Joules – Because work is calculated as force times distance, it is expressed in newtons times meters (N x m) • 1 Nm = 1 J = 1 Kg x m 2/s 2 • Because all of these units are equivalent, when solving a particular problem, you can choose which unit to use – Substituting equivalent units will often help you cancel out other units in a problem

Work, Power, and Machines • In order to lift the barbell above his head the weight lifter need to apply a force which opposes the downward acting force of gravity on the mass of the barbell. The distance from the floor to above the lifters head is 2 meters.

Work, Power, and Machines • Mass of barbell = 25 + 25 = 50 kg Weight of barbell = mass x acceleration due to gravity F=mxg F = 50 Kg x 9. 8 m/s 2 = 490 Newtons Work done = force x distance Work done = 490 Kgm/s 2 x 2 m = 980 Kgm 2/s 2 = 980 Joules

Work, Power, and Machines • In the example above the work done by the weight lifter in lifting the weights was 980 joules. In order to do this work energy had to be transferred. 980 joules of chemical energy from food eaten by the weight lifter was transferred to 980 joules of gravitational potential energy to the barbell. Thus the amount of work done is equal to the energy transferred from one form to another.

Work, Power, and Machines • Is any work being done?

Work, Power, and Machines

Work, Power, and Machines • Power: is the rate at which work is done, or how much work is done in a given amount of time • Power = work / time • P = W / t • Power is measured in watts – One watt is the amount of power needed to do 1 joule of work in 1 second – Do not confuse the symbol for work (W) which is italic, with the symbol for watt, W

Work, Power, and Machines

Work, Power, and Machines • When doing a chin-up, a physics student lifts her 42. 0 -kg body a distance of 0. 25 meters in 2 seconds. What is the power delivered by the student's biceps?

Work, Power, and Machines • To raise her body upward at a constant speed, the student must apply a force which is equal to her weight (m • g). The work done to lift her body is • W = F * d = (411. 6 N) * (0. 250 m) W = 102. 9 J • The power is the work/time ratio which is (102. 9 J) / (2 seconds) = 51. 5 Watts (rounded)

Work, Power, and Machines • Your household's monthly electric bill is often expressed in kilowatt-hours. One kilowatt-hour is the amount of energy delivered by the flow of l kilowatt of electricity for one hour. Use conversion factors to show many joules of energy you get when you buy 1 kilowatt-hour of electricity.

Work, Power, and Machines • Using conversion factors, it can be shown that 1 kilo-watt*hour is equivalent to 3. 6 x 106 Joules. First, convert 1 k. W-hr to 1000 Watt-hours. Then convert 1000 Watt-hours to 3. 6 x 106 Watt-seconds. Since a Wattsecond is equivalent to a Joule, you have found your answer.

Work, Power, and Machines • Machines help do work by changing the size of an input force, the direction of the force, or both

Work, Power, and Machines • Mechanical advantage: – Is the ratio between the output force and the input force – Also, it is equal to the ratio between the input distance and the output distance – If friction is ignored

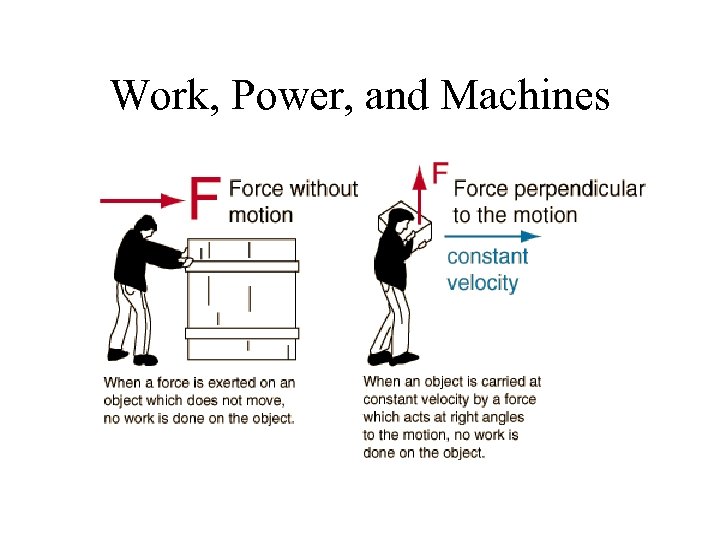
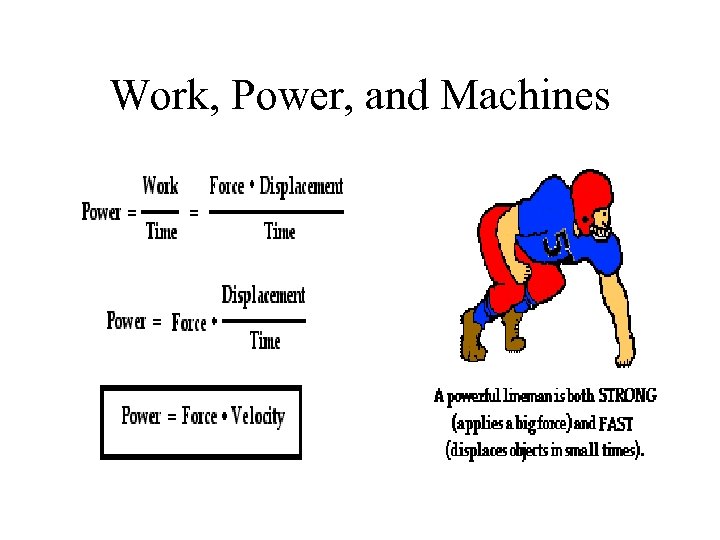
Work, Power, and Machines • Mechanical advantage = – Output force / input force = input distance / output distance • Machine with a mechanical advantage greater than 1 – Multiplies the input force – Helps you move or lift a heavy object • Machine with a mechanical advantage less than 1 does not multiply force but increases distance and speed

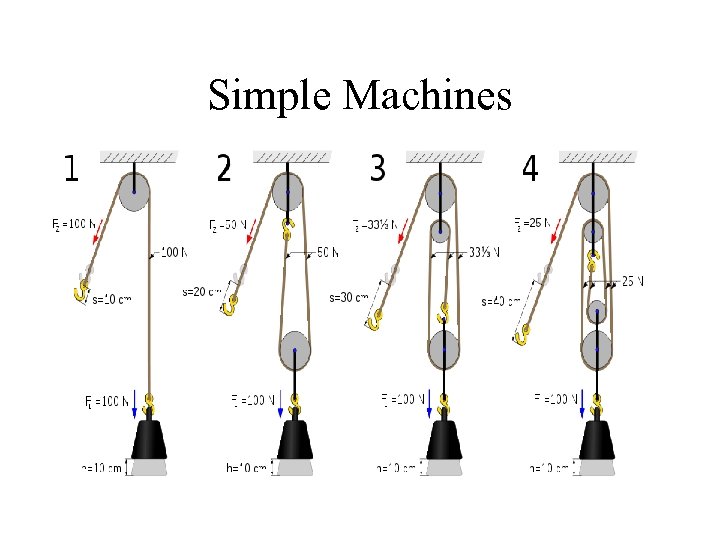
Simple Machines • Machines are either modifications of simple machines or combinations of several simple machines • Six types of simple machines: – – – Simple lever Pulley Wheel and axle Simple inclined plane Wedge Screw

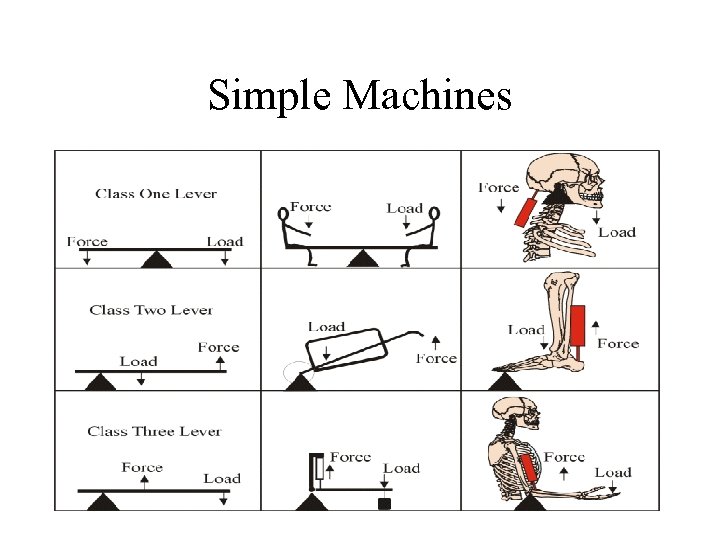
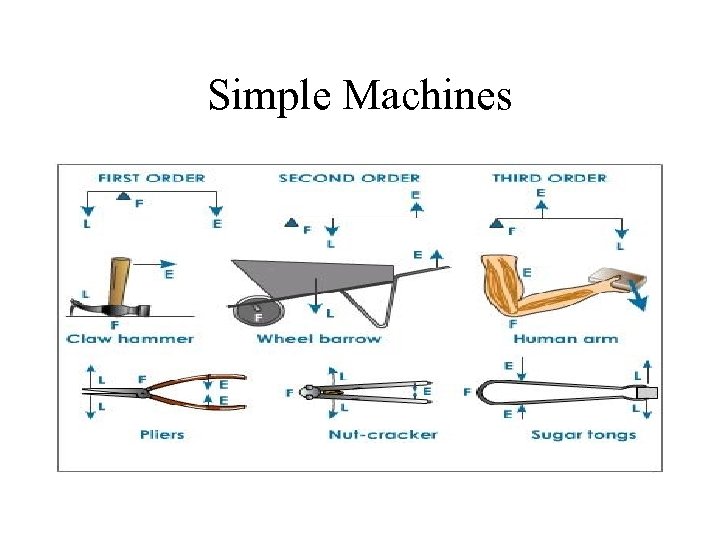
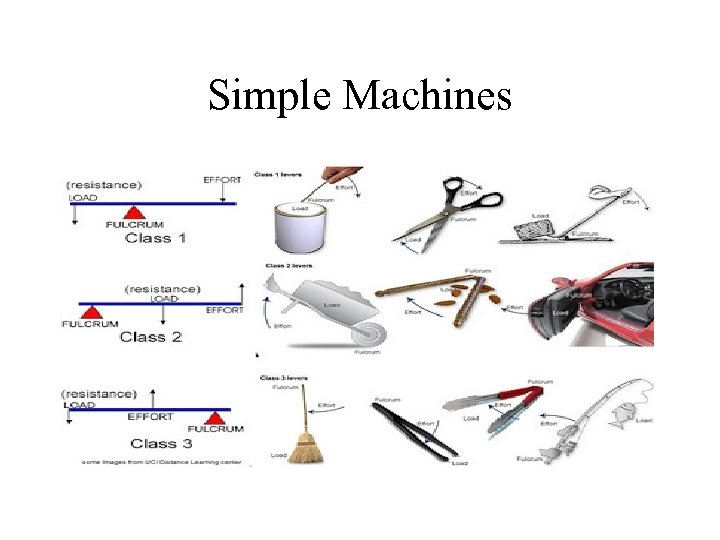
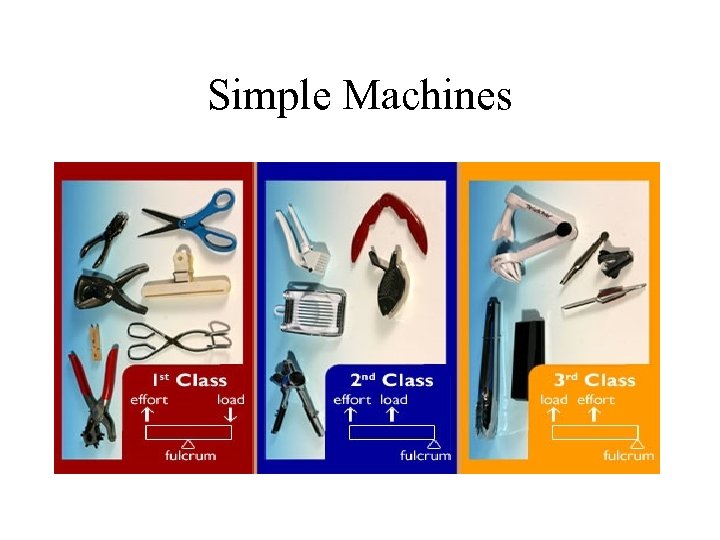
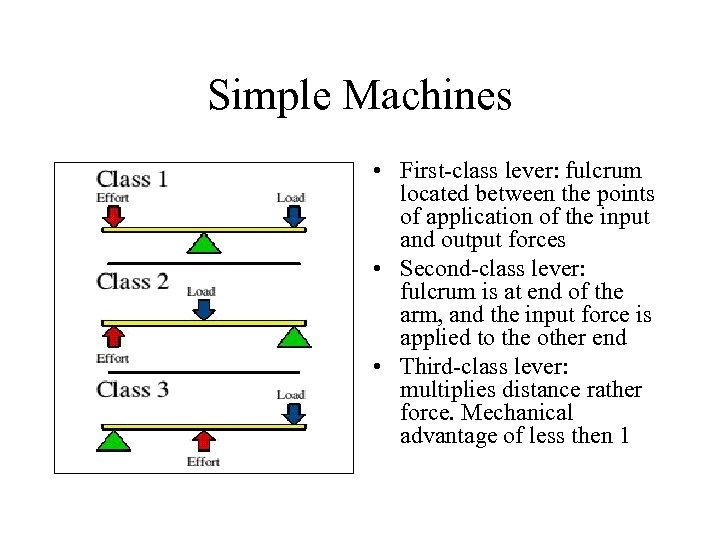Simple Machines • First-class lever: fulcrum located between the points of application of the input and output forces • Second-class lever: fulcrum is at end of the arm, and the input force is applied to the other end • Third-class lever: multiplies distance rather force. Mechanical advantage of less then 1

Simple Machines

Simple Machines

Simple Machines

Simple Machines

Simple Machines

Simple Machines

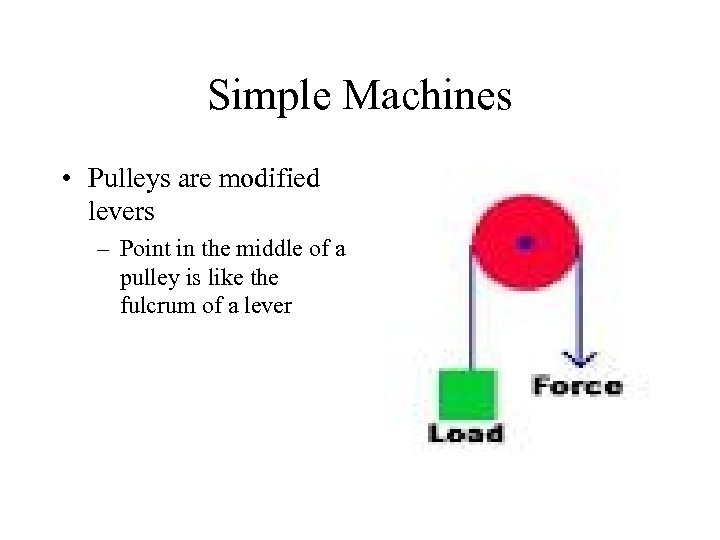Simple Machines • Pulleys are modified levers – Point in the middle of a pulley is like the fulcrum of a lever

Simple Machines

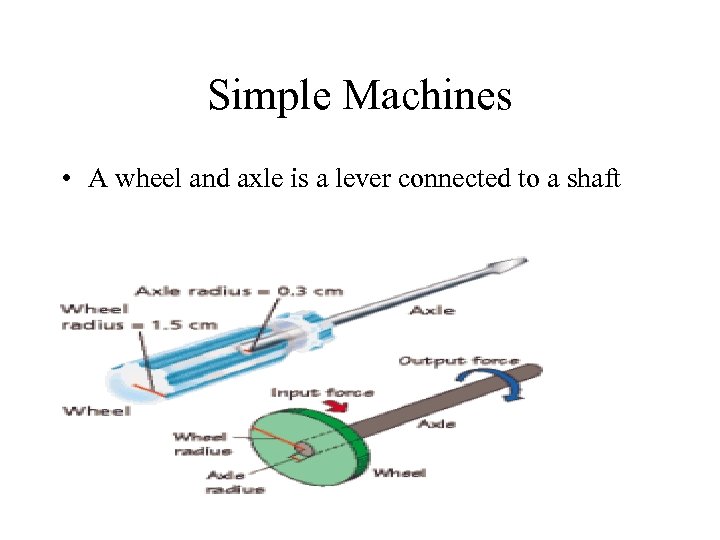Simple Machines • A wheel and axle is a lever connected to a shaft

Simple Machines

Simple Machines • Inclined plane: pushing an object up an inclined plane requires less input force than lifting the same object does.

Simple Machines

Simple Machines

Simple Machines • Wedge: formed when two inclined planes are placed back to back – Like pushing a ramp instead of pushing something up a ramp – Turns a single downward force into two forces directed out to the sides

Simple Machines

Simple Machines • Screw is an inclined plane wrapped around a cylinder – The threads on a screw are inclined planes • Gentle sloping threads requires a small force to act over a long distance • Steeper slopes requires more force over less distance – Drill bits – Jar lids

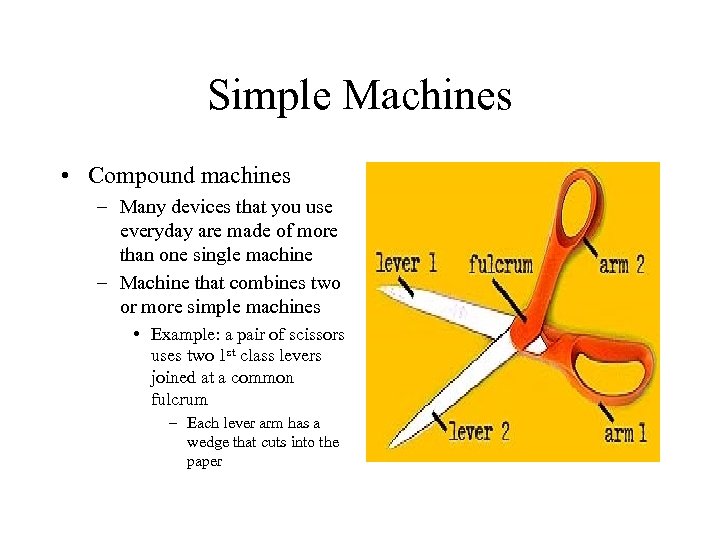Simple Machines • Compound machines – Many devices that you use everyday are made of more than one single machine – Machine that combines two or more simple machines • Example: a pair of scissors uses two 1 st class levers joined at a common fulcrum – Each lever arm has a wedge that cuts into the paper

What is Energy? • Energy: – Ability to do work – Whenever work is done, energy is transformed or is transferred from one system to another system – Measured in Joules (same as in Work)

What is Energy? • Potential Energy (PE): – Energy of position because it results from the relative positions of objects in a system

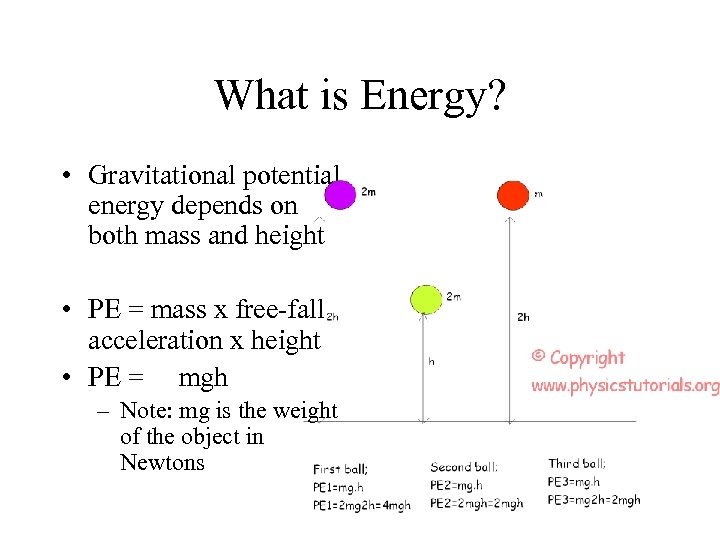What is Energy? • Gravitational potential energy depends on both mass and height • PE = mass x free-fall acceleration x height • PE = mgh – Note: mg is the weight of the object in Newtons

What is Energy?

What is Energy?

What is Energy?

What is Energy? • Kinetic Energy: energy of motion – – Depends on both the mass and speed of an object KE = ½ x mass x speed squared KE = ½mv 2 = ½ kg x m 2/s 2 Why are car crashes more dangerous at high speeds? • Depends on speed more than it depends on mass • Speed is squared, so a small change in speed causes a large change in KE

What is Energy?

What is Energy? • Mechanical energy: sum of the kinetic energy and potential energy in a system – Mechanical engineering • Design machines • Chemistry: chemical potential energy • Photosynthesis: energy from the sun

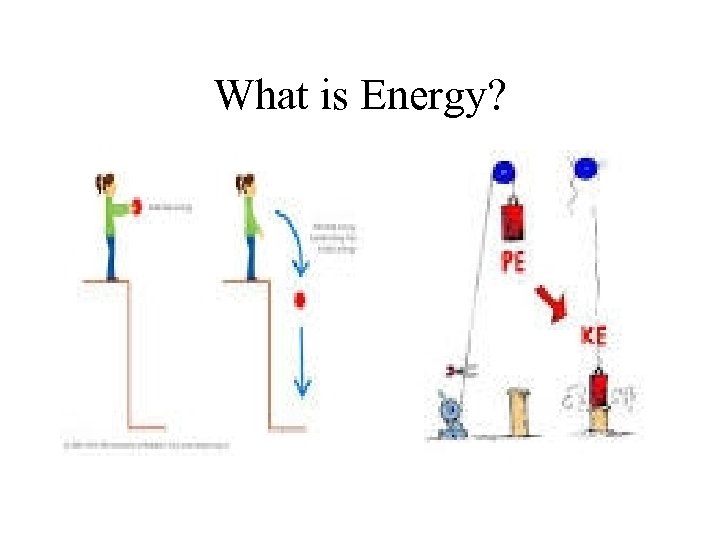
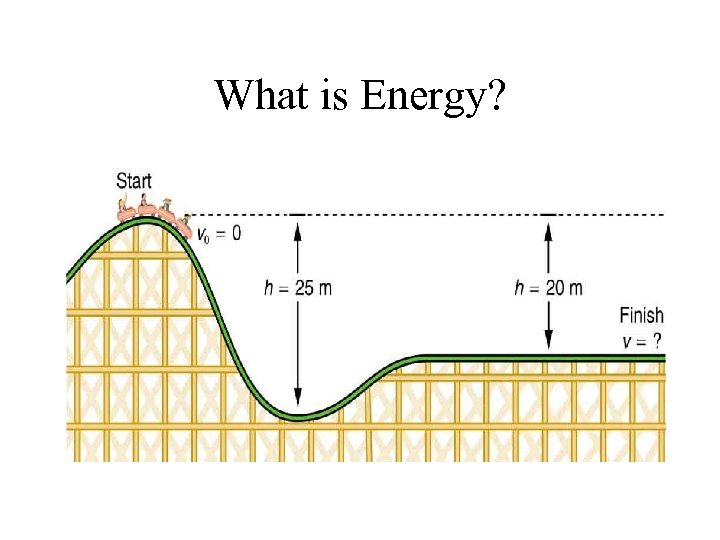
Conservation of Energy • The total amount of energy in the universe never changes, although energy may change from one form to another • Energy cannot be created or destroyed – Potential becomes kinetic – Kinetic becomes potential

Conservation of Energy • Efficiency of machines: – Not all work done by a machine is useful work • Friction generates heat – Measured as a percentage: ratio of useful work output to work input – Efficiency = useful work output/work input

Conservation of Energy • A diesel engine with an efficiency of 0. 39 requires 750 J of work to be done on its pistons. • How much useful work is done by the diesel engine? • 1. List the given and unknown values. • Given: efficiency = 0. 39 • work done on the machine (input) = 750 J • Unknown: useful work done by the machine (output) = ? J

Conservation of Energy • 2. Use the efficiency equation, and rearrange it to solve for useful work done by the • machine (output). • Efficiency = useful work done by the machine output / work done on the machine input • efficiency × work done by the machine (input)= × useful work done by the machine output/work done on the machine input x work done on the machine input • = useful work done by the machine (output)

Conservation of Energy • 3. Substitute the values for the work done on the machine and the efficiency into the • equation, and solve. • useful work done by the machine (output) = (0. 39) × (750 J) • useful work done by the machine (output) = 290 J

Conservation of Energy