CHAPTER 13 Options on Futures In this chapter

CHAPTER 13 Options on Futures In this chapter, we discuss option on futures contracts. This chapter is organized into: 1. Characteristics of Options on Physicals and Options on Futures. 2. The Market for Options on Futures 3. Pricing of Options on Futures 4. Price Relationship Between Options on Physicals and Options on Futures 5. Put-Call Parity for Options on Futures 6. Options on Futures and Synthetic Futures 7. Risk Management with Options on Futures Chapter 13 1

Characteristics of Options on Physicals and Options Futures Recall from Chapter 12 that options are written for a prespecified amount of a pre-specified asset at a pre-specified price that can be bought or sold at a pre-specified time period. Call Options The buyer of a call option has the right but not the obligation to purchase. The seller of a call option has the obligation to sell. Put Options. The buyer of a put option has the right but not the obligation to sell. The seller of a put option has the obligation to purchase. Chapter 13 2

Characteristics of Options on Physicals and Options Futures Prices of options on futures are closely related to prices of options on the underlying good. Call Option on Futures Upon exercising a option on futures, the call owner: – Receives a long position in the underlying futures at the settlement price prevailing at the time of exercise. – Receives a payment that equals the settlement price minus the exercise price of the option on futures. The call owner would not exercise if the futures settlement price did not exceed the exercise price. Upon exercise, the call seller: – Receives a short position in the underlying futures at the settlement price prevailing at the time of exercise. – Pays the long trader the futures settlement price minus the exercise price. Chapter 13 3

Characteristics of Options on Physicals and Options Futures On February 1, a trader buys a call option on a MAR euro futures contract with an exercise price of $0. 44 per euro. On February 15, the call owner decides to exercise the call option. The futures settlement price is $. 48. After gathering all the information, the owner has: Future settlement price The exercise price The euro futures maturing Euro contract amount = $. 48 = $. 44/euro = March = 125, 000 euros Upon exercise, the call owner: – Receives a long position in the MAR euro futures contract. – Receives a payment = F 0 – E $. 48 -. 44 (125, 000) = $5000 Upon exercise, the call seller: – Receives a short position in the euro futures. – Pay $5, 000. The traders can offset or hold their futures positions. Chapter 13 4

Characteristics of Options on Physicals and Options Futures Put Option on Futures Upon exercising a option on futures, the put owner: – Receives a short position in the underlying futures contract at the settlement price prevailing at the time of exercise. – Receives a payment that equals the exercise price minus the futures settlement price. The put owner would not exercise unless the exercise price exceeded the futures settlement price. Upon exercise, the put seller: – Receives a long position in the underlying futures contract. – Pays the exercise price minus the settlement price. Chapter 13 5

Characteristics of Options on Physicals and Options Futures On April 1, a trader buys a put option on a MAY wheat futures contract. The exercise price is $2. 40/bushel and wheat contract is for 5, 000 bushels. On April 4, the owner of the call option decides to exercise. The futures settlement price is $2. 32/bushel. Exercise price Wheat contract Futures settlement price The wheat futures matures = $2. 40/bushel = 5, 000 bushels = $2. 32/bushel. = May Upon exercise, the put owner: – Receives a short position MAY Wheat futures contract. – Receives a payment = F 0 – E $2. 40 -$2. 32 (5, 000) = $400 Upon exercise, the put seller: – Receives a long position MAY Wheat futures contract. – Pays $400. The traders can offset or hold their futures positions. Chapter 13 6

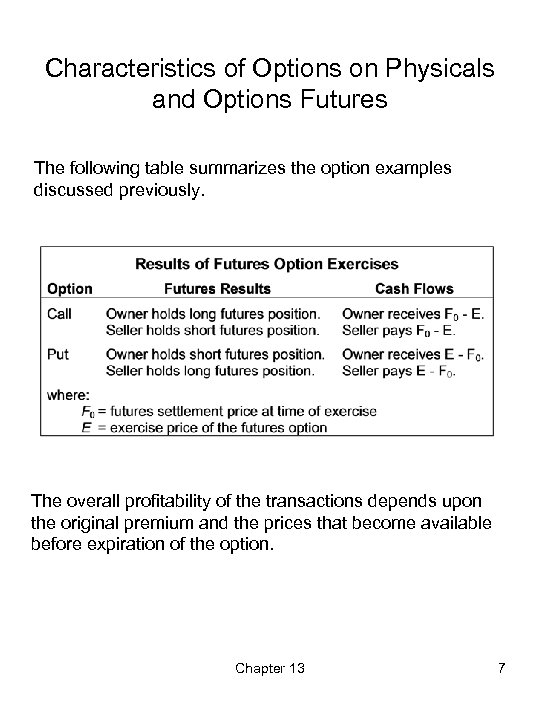Characteristics of Options on Physicals and Options Futures The following table summarizes the option examples discussed previously. The overall profitability of the transactions depends upon the original premium and the prices that become available before expiration of the option. Chapter 13 7

The Market of Options on Futures Figure 13. 1 presents some illustrative quotations for options on futures. Insert figure 13. 1 here Chapter 13 8

The Market of Options on Futures Table 13. 1 shows the trading volume for options on futures by type of commodity in the fiscal year ending September 30, 1995. Chapter 13 9

The Market of Options on Futures Chapter 13 10

The Market of Options on Futures Chapter 13 11

The Market of Options on Futures Chapter 13 12

Pricing Options on Futures Recall from Chapter 12: European Options European options can be exercised only on the maturity date. American Options American options can be exercised any time prior to maturity. The Black-Scholes model focus best on European options which avoids problems with early exercise and dividends. When there is a dividend and the dividend rate varies, the Black-Scholes model is not suitable for valuing options on futures. The Black-Scholes model can be modified forward option pricing. Chapter 13 13

Graphical Approach to American Options on Futures Figure 13. 2 illustrates how European options prices are good approximations for American futures option prices Insert figure 13. 2 here Chapter 13 14

Black-Scholes Model for Options on Forward Contracts The Black-Scholes equation for option on forward contracts is: Where r = risk-free rate of interest t = time until expiration for the forward and the option F 0, t = forward price for a contract expiring at time t α = standard deviation of the forward contract’s price If there were no uncertainty, N(d 1*) and N(d 2*) will equal 1 and the equation would simplify to: Cf = e-rt[F 0, t - E] Chapter 13 15

European Versus American Option on Futures European Options Early exercise of an option on a non-dividend paying stock is not recommended: – Recall that upon exercising, the call owner receives the intrinsic value (S – E). – Exercising a call discards the excess value of the option over and above S – E. American Options Early exercise of a dividend paying futures option has benefits and costs – Benefit: exercise provides an immediate payment of F – E which can earn interest until expiration ert [F - E]. – Cost: sacrifice of option value over and above intrinsic value F – E. Chapter 13 16

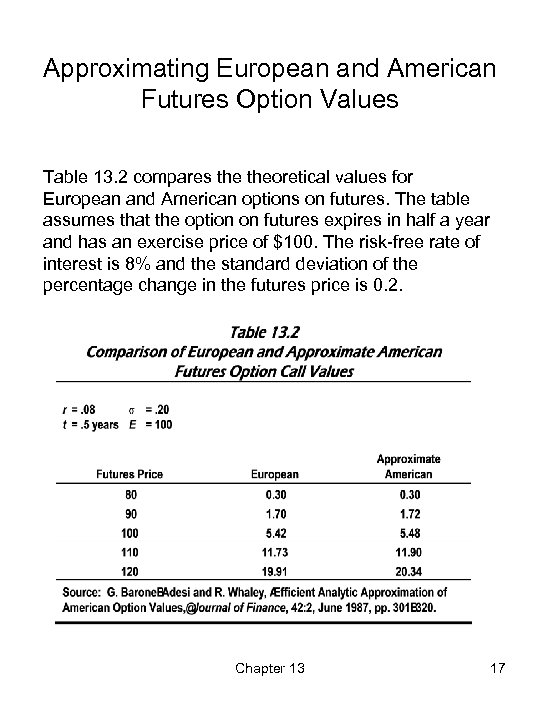Approximating European and American Futures Option Values Table 13. 2 compares theoretical values for European and American options on futures. The table assumes that the option on futures expires in half a year and has an exercise price of $100. The risk-free rate of interest is 8% and the standard deviation of the percentage change in the futures price is 0. 2. Chapter 13 17

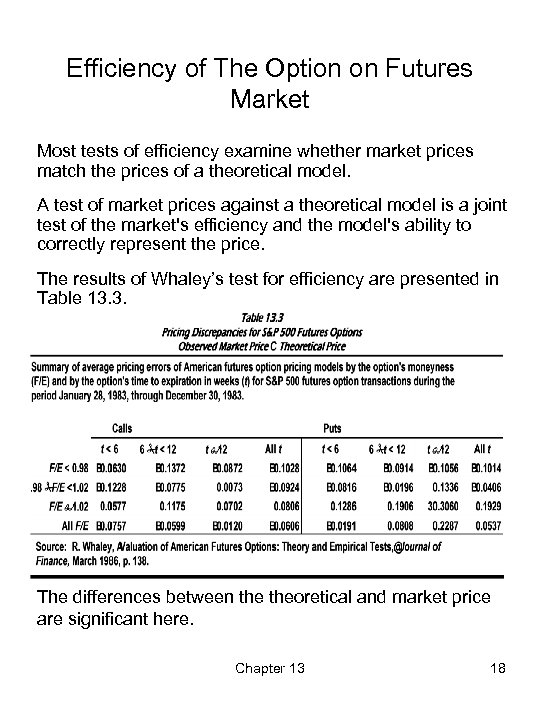Efficiency of The Option on Futures Market Most tests of efficiency examine whether market prices match the prices of a theoretical model. A test of market prices against a theoretical model is a joint test of the market's efficiency and the model's ability to correctly represent the price. The results of Whaley’s test for efficiency are presented in Table 13. 3. The differences between theoretical and market price are significant here. Chapter 13 18

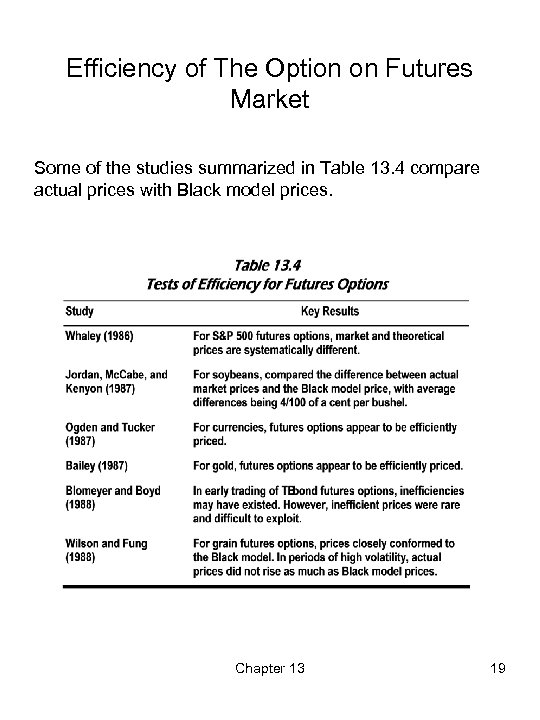Efficiency of The Option on Futures Market Some of the studies summarized in Table 13. 4 compare actual prices with Black model prices. Chapter 13 19

Price Relationship Between Options on Physicals and Options on Futures In this section, the pricing relationship between options on physicals and options on futures is considered, specifically for call options. The analysis is organized as follows: 1. European options 2. American options on underlying assets with no cash flow 3. American options on underlying assets with cash flow Chapter 13 20

Price Relationship Between Options on Physicals and Options on Futures The following assumption will be held for this analysis: 1. The options have the same expiration and exercise price. 2. The options are on the same underlying commodity. – One option is on the commodity itself. – One option is on the futures on the commodity. Chapter 13 21

European Options on Physicals and Futures Recall from Chapter 12 that at expiration a call option on the physical will be worth: S-E For European options on futures, exercise can occur only at expiration, so it must be that: Ft, t - E = St - E For European options the exercise value for options on physicals and options on futures is the same. Chapter 13 22

American Options on Physicals and Futures with No Underlying Cash Flows For American options, any difference in value between options on physicals and options on futures results from the early exercise privilege. Table 13. 5 shows the exercise values that the option on the futures can have given the option on physicals in percentage terms. The risk-free rate is assumed to be 15% and the percentage change in the underlying assets is. 25. Chapter 13 23

American Options on Physicals and Futures with Underlying Cash Flows This analysis is particularly relevant to options on stock indexes and options on stock index futures. Cash flows from the underlying good reduce its value. – When stock pays a dividend, the stock price drops by approximately the amount of the dividend. These cash flows affect both the option on the physical and the option on the futures. The analysis focuses on underlying physical asset paying a continuous dividend (cash flow) equal to the risk-free rate of interest. Under conditions of certainty, a futures call option is worth the present value of: F 0, t – E, t = 0 Based on the perfect markets Cost-of-Carry Model the futures price will be: F 0, t = S 0(1 + C) Chapter 13 24

American Options on Physicals and Futures with Underlying Cash Flows For financial futures, the cost of carry is the risk-free interest rate. Assume a continuous dividend equal to the risk-free rate of interest. In this case, the cost of carry is zero, so the futures call option price equals: F 0, t = S 0 erte-rt = S 0 Substituting the value of F 0, t into the Black-Scholes OPM gives an adjusted Black-Scholes OPM of: where: Cf = the price of a call option on the futures After adjusting the Black-Scholes model for continuous paying dividend: The values for the call option on the futures and physical are the same. That is, d 1* = d 1, and d 2* = d 2. Chapter 13 25

Relative Prices of Options on Physicals and Futures The implications of this analysis for various dividend rates are: Chapter 13 26

Put-Call Parity for Options on Futures Recall that Put-Call Parity specifies a relationship between the price of call and put options. For non-dividend paying assets put-call parity equals: C - P = S 0 - Ee-rt where: C P E S 0 r t = = = value of a call with exercise price E value of a put with exercise price E exercise price of both the call and put stock price risk-free rate of interest time until the options expire Chapter 13 27

Put-Call Parity for Options on Futures Before expiration, for options on futures, the relationship can be expressed as: Cf - Pf = (F 0, t - E)e-rt where: Cf = futures call option with exercise price E Pf = futures put option with exercise price E F 0, t = current futures price E = common exercise price for Cf and Pf r = risk-free rate t = time until expiration for the futures and options Comparing both equations shows the similar structure of put-call parity for options on physicals and on futures. Chapter 13 28

Put-Call Parity for Options on Futures Using continuous compounding, the Cost-of-Carry Model for a perfect market is: F 0, t = S 0 ert Substituting this expression for the futures price into the above equation gives: Cf - Pf = (S 0 ert - E)e-rt = S 0 - Ee-rt Chapter 13 29

Options on Futures and Synthetic Futures A position that duplicates the profits and losses from a futures, but consists of positions in other instruments. Creating synthetic futures equals: Futures Call - Futures Put = Synthetic Futures Table 13. 6 summarizes the rules for constructing synthetic positions. Chapter 13 30

Risk Management with Options on Futures This section explores examples related to risk management including: – Portfolio Insurance – Synthetic Portfolio Insurance and Put-Call Parity – Risk and Return in Insured Portfolios Chapter 13 31

Risk Management with Options on Futures Example Assume: a stock index is currently at $100. Stocks in the index pay no dividends, and the expected return on the index is 10% with a standard deviation of 20%. A put option on the index with an exercise price of $100 is available and costs $4. Consider three investment strategies: Portfolio A : (uninsured) Buy the index; total investment $100. Portfolio B: (half insured) Buy the index and one-half of a put; total investment $102. Portfolio C: (fully insured) Buy the index and one put; total investment $104. At expiration, the three portfolios will have profits and losses computed using the following equations: Portfolio A: Index Value - $100 Portfolio B: Index Value +. 5 MAX{0, Index Value – $100} - $102 Portfolio C: Index Value + MAX{0, Index Value – $100} - $104 Chapter 13 32

Risk Management with Options on Futures Figure 13. 4 graphs the profits and losses of these 3 portfolios. Insert Figure 13. 4 here Chapter 13 33

Portfolio Insurance Recall that in portfolio insurance, a trader transacts to insure that the value of a portfolio does not fall below a given amount. Based on figure 13. 4, portfolio C is an insured portfolio: The value of portfolio C cannot fall below $100. To create portfolio C, a trader bought the index at $100 and bought an index put with an exercise price of $100. The worst possible loss on portfolio C is $4. Portfolio C must always be worth at least $100 because the value can not fall below $100, so it an insured portfolio. Chapter 13 34

Synthetic Portfolio Insurance and Put. Call Parity Recall that a synthetic call could be created from a long position in the underlying good plus a long put. Thus a synthetic call is: Synthetic Call = Put + Index From Figure 13. 4, the Put + Index portfolio has the same profits and losses as a call option with an exercise price of $100. Applying the put-call parity equation to the index example: Call = Put + Index - Ee-rt where: E = exercise price on the index option An instrument with the same value and profits and losses as a call can be created by holding a long put, long index, and borrowing the present value of the exercise price. Chapter 13 35

Synthetic Portfolio Insurance and Put. Call Parity From the put-call parity, there is another way to create a portfolio that exactly mimics the insured portfolio’s value at expiration. Call + E-rt = Put + Index We can hold a long call plus investing the present value of the exercise price in the risk-free asset. Chapter 13 36

Risk’s Return on Insured Portfolios Each of the portfolios A-C has different risk characteristics. To explore the risk properties of the portfolios assume that the return on the index follows a normal distribution with a mean of 10% and a standard deviation of 20%. Terminal Values for Portfolios A-C. The portfolio values at expiration depend on the price of the index at expiration. For each, the terminal value is: Portfolio A = Index Portfolio B = Index + MAX{0, . 5(100. 00 - Index)} Portfolio C = Index + MAX{0, 100. 00 - Index} What is the probability that each of the portfolios will have a terminal value equal to or less than $100? Chapter 13 37

Risk Return in Insured Portfolios Table 13. 7 shows some portfolio values and the probabilities that each portfolio will be equal to or less than the given terminal value at the expiration date. Chapter 13 38

Risk Return in Insured Portfolios Figure 13. 5 graphs the terminal portfolio values from $50 to $170 and shows the probability for each portfolio that the terminal portfolio value will be below or equal to the given amount. Insert Figure 13. 5 here Chapter 13 39

Risk Return in Insured Portfolios Returns on Portfolios A-C Table 13. 8 shows the probability that each portfolio will achieve a return greater than a specified return. This is a tradeoff between return and risk on the portfolios. The portfolios having a higher return also have a higher risk. Chapter 13 40

Risk Return in Insured Portfolios Figure 13. 6 graphs the probabilities for each portfolio for a range of returns from -50% to 50%. Insert Figure 13. 6 here Chapter 13 41

Why Options on Futures Some reasons for the popularity of options on futures are: 1. A futures position exposes a trader to a theoretically unlimited risk of gain or loss, but this is not true for the buyer of a futures option. 2. Options on futures dominate options on physicals in some markets because the futures market for some goods is much more liquid than the market for the physical good itself. 3. Options on futures generally require less investment than options on the physical good itself. Chapter 13 42