Chapter 13 NP-Completeness x 1 x 2 12

Chapter 13 NP-Completeness x 1 x 2 12 11 NP-Completeness x 3 22 13 21 x 4 32 23 31 33 1

Dealing with Hard Problems • What to do when we find a problem that looks hard… I couldn’t find a polynomial-time algorithm; I guess I’m too dumb. NP-Completeness 2

Dealing with Hard Problems • Sometimes we can prove a strong lower bound… (but not usually) I couldn’t find a polynomial-time algorithm, because no such algorithm exists! NP-Completeness 3

Dealing with Hard Problems • NP-completeness let’s us show collectively that a problem is hard. I couldn’t find a polynomial-time algorithm, but neither could all these other smart people. NP-Completeness 4

Polynomial-Time Decision Problems • To simplify the notion of “hardness, ” we will focus on the following: – Polynomial-time as the cut-off for efficiency so O(n 10) and 107 n are efficient? (Not practically speaking, but don’t occur in practice much. ) – Decision problems: output is 1 or 0 (“yes” or “no”) Note we change form of problem to make verifying it easier – Want a yes/no answer. Examples: • Does a given graph G have an Euler tour? • Does a text T contain a pattern P? • Does an instance of 0/1 Knapsack have solution of benefit K? • Does a graph G have an MST with weight at most K? NP-Completeness 5

The Complexity Class P • Use term “language” to mean problem. Use term “accepted” to mean “determine if we can answer yes to the problem”. • A complexity class is a collection of languages (representing problems) • P is the complexity class consisting of all languages that are accepted by polynomial-time algorithms. In other words, I can determine membership in the language in polynomial-time. NP-Completeness 6

The term non-determinism • NP is the complexity class consisting of all languages accepted by polynomial-time nondeterministic algorithms. • non-determinism does not mean that the results are different each time. • non-determinism does mean that you aren’t specifying how the choices are made. • Example: Someone asks you to verify that you can fill the knapsack with items of value K or more. You construct a set of items that has that property. The part that could be nondeterministic is how you select the items. NP-Completeness 7

Other ways of thinking of NP • An NP problem is one in which the answer can be checked in polynomial time. In other words, if someone tells you what choice to make whenever you aren’t sure, can you verify their suggestions in polynomial time? • Think about having a “fat” machine. Anytime you don’t know which choice to make, try all choices simultaneously. You are allowed to “clone” your resources without penalty. NP-Completeness 8

Can you think of an example that can’t even be checked in Polynomial time? Example: This number is prime. n=1 (a single number) Example: This TSP (travelling salesperson problem) solution is optimal – Note the problem has not been simplified. If we said, this graph has a TSP <100, we would be fine. Example: Generate all permutations. We say this problem is “poorly formed” as the output itself is exponential. NP-Completeness 9

The Complexity Class NP • We know: P is a subset of NP, but is it a proper subset? Major open question: P=NP? • Most researchers believe that P and NP are different. NP-Completeness 10

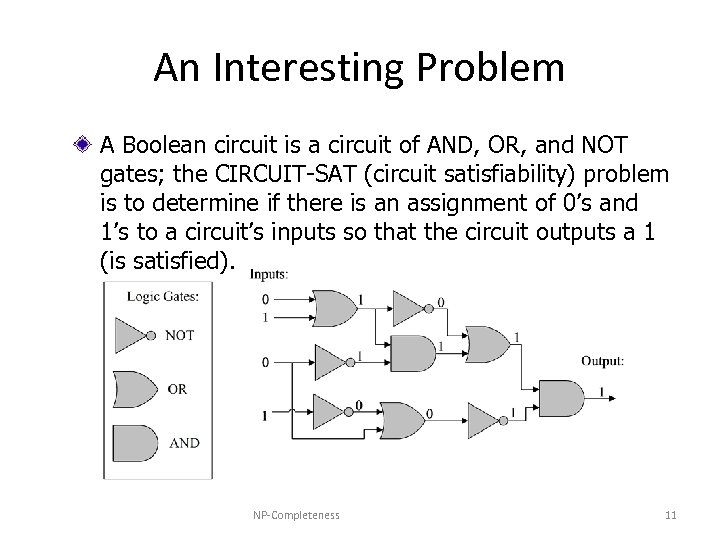An Interesting Problem A Boolean circuit is a circuit of AND, OR, and NOT gates; the CIRCUIT-SAT (circuit satisfiability) problem is to determine if there is an assignment of 0’s and 1’s to a circuit’s inputs so that the circuit outputs a 1 (is satisfied). NP-Completeness 11

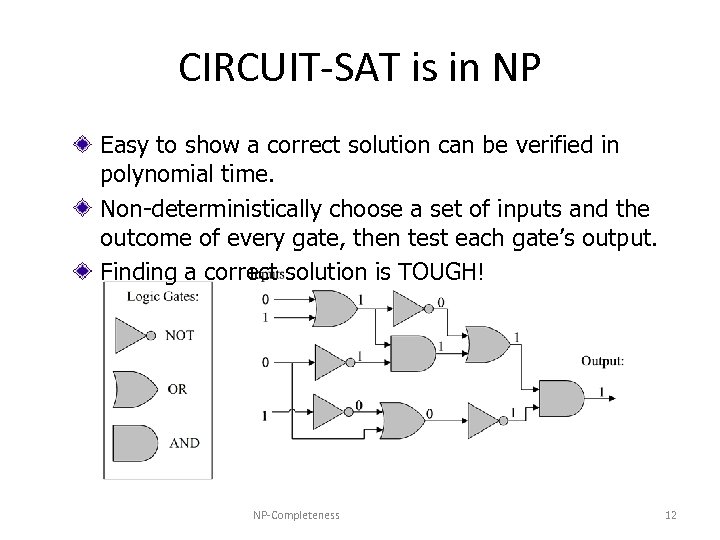CIRCUIT-SAT is in NP Easy to show a correct solution can be verified in polynomial time. Non-deterministically choose a set of inputs and the outcome of every gate, then test each gate’s output. Finding a correct solution is TOUGH! NP-Completeness 12

NP-hard • A problem L is NP-hard (is the hardest problem in the set NP) if every problem (“the complete set”) in NP can be reduced to L in polynomial time. • That is, for each language M in NP, we can take an input x for M, transform it in polynomial time to an input x’ for L such that x is in M if and only if x’ is in L. • An NP-hard problem that is also in NP (can be verified in polynomial time) is termed NP-complete • This transformation time is important- as otherwise the transformation could be doing all the work. NP-Completeness 13

NP-hard • This transformation time is important- as otherwise the transformation could be doing all the work. Example: The hitting set problem is an NP-complete problem in set theory. For a given list of sets, a hitting set is a set of elements so that each set in the given list is 'touched' by the hitting set. In the hitting set problem, the task is to find a small hitting set. Map finding a hitting set into min(a, b). Map as follows. Let a be the size of the smallest hitting set that includes X. Let b be the size of the smallest hitting set that does not include X. Now the “mapped to” problem, just has to compare two things. Almost all the work happened in the transformation. So we learn nothing about the difficulty of min by this transformation. NP-Completeness 14

NP-Completeness • We demonstrate NP-hard by mapping known problems to problems of unknown difficulty. NP poly-time NP-Completeness L 15

Mapping • Often students get confused which way to map problems. • I have two problems H (hard), and U(unknown), which way do I map the problem to learn something? H U or U H? • H U, as when we solve U, we also solve H, making a solution to U at least as hard as H. • If you map it the other way, the hard problem could be doing MUCH MORE than the easy problem. The easy problem could be solved as a side effect. NP-Completeness 16

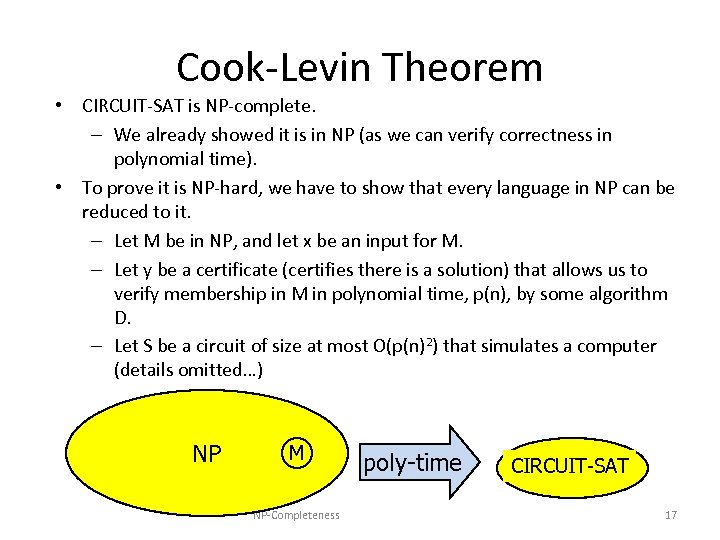Cook-Levin Theorem • CIRCUIT-SAT is NP-complete. – We already showed it is in NP (as we can verify correctness in polynomial time). • To prove it is NP-hard, we have to show that every language in NP can be reduced to it. – Let M be in NP, and let x be an input for M. – Let y be a certificate (certifies there is a solution) that allows us to verify membership in M in polynomial time, p(n), by some algorithm D. – Let S be a circuit of size at most O(p(n)2) that simulates a computer (details omitted…) NP M NP-Completeness poly-time CIRCUIT-SAT 17

Some Thoughts about P and NP • Belief: P is a proper subset of NP. • Implication: the NP-complete problems are the hardest in NP. • Why: Because if we could solve an NP-complete problem in polynomial time, we could solve every problem in NP in polynomial time. • That is, if any NP-complete problem is solvable in polynomial time, then P=NP. • Since so many people have attempted without success to find polynomial -time solutions to NP-complete problems, showing your problem is NPcomplete is equivalent to showing that a lot of smart people have worked on your problem and found no polynomial-time algorithm. NP-Completeness 18

NP Complete. How do we use it? Problem Reduction • A language M is polynomial-time reducible to a language L if every instance x for M can be transformed in polynomial time to an instance x’ for L such that x is in M if and only if x’ Inputs: in L. is – Denote this by M L. • CIRCUIT-SAT is NP-complete: 0 1 – CIRCUIT-SAT is in NP – For every M in NP, M CIRCUIT-SAT. NP-Completeness 1 0 1 Output: 1 0 1 19

Transitivity of Reducibility • If A B and B C, then A C. – A C, since polynomials are closed under composition. NP-Completeness 20

SAT • A Boolean formula is a formula where the variables and operations are Boolean (0/1): – (a+b+¬d+e)(¬a+¬c)(¬b+c+d+e)(a+¬c+¬e) – OR: +, AND: (times), NOT: ¬ – termed CNF: conjunctive normal form: series of subexpressions connected with and, each part of subexpression connected with or. Called “normal” as every boolean formula can be put in this form. Joined – similarly DNF: disjunctive normal form is the or of ands. De. Morgan’s law is helpful in switching forms. Two or more alternate forms NP-Completeness 21

CNF-SAT: Given a Boolean formula S, is S satisfiable, that is, can we assign 0’s and 1’s to the variables so that S is 1 (“true”)? – Easy to see that CNF-SAT is in NP: • Non-deterministically choose an assignment of 0’s and 1’s to the variables and then evaluate each clause. If they are all 1 (“true”), then the formula is satisfiable. NP-Completeness 22

SAT is NP-complete • Reduce CIRCUIT-SAT to SAT. – Given a Boolean circuit, make a variable for every input and gate. – We might be tempted just to create the formula by nesting the gate formulas, but the nesting could be pretty bad. – Instead, create a sub-formula for each gate, characterizing its effect. Form the formula as the output variable AND-ed with all these sub-formulas: • Example: m((a+b)↔e)(c↔¬f)(d↔¬g)(e↔¬h)(ef↔i)… Inputs: a b c d e h i f g j k n NP-Completeness The formula is satisfiable if and only if the Output: Boolean circuit m is satisfiable. 23

But not yet in CNF m((a+b)↔e)(c↔¬f)(d↔¬g) (e↔¬h)(ef↔i)… • • We have the and of clauses. We change each clause to CNF : – Build a truth table for the clause e ab NP-Completeness a 1 1 0 0 b 0 0 1 1 0 0 e 0 1 1 0 e ab 1 0 0 1 0 1 24

• Could express e ab either postively or negatively. • Positively: (abe+a¬b¬e + ¬a ¬b¬e) • Negatively: ¬(ab¬e +a¬be+ ¬a¬be) • Since we want CNF, the opposite of the negatively stated answer is most helpful NP-Completeness 25

Converting to CNF continued • Need to worry about form. Worry about Not. • for each 0 in result, show the values (in DNF) • then ¬B is the “or” of all the 0 generating choices • You can get B by De. Morgan’s law • Example c ab • ¬B = ab¬c + a¬bc + ¬a¬bc • B = (¬a+¬b+c)(¬a+b+¬c)(a+¬b+¬c)(a+b+¬c) • Repeat for all clauses and “and” together NP-Completeness 26

3 SAT The SAT problem is still NP-complete even if it is in CNF and every clause has just 3 literals (a variable or its negation): – (a+b+¬d)(¬a+¬c+e)(¬b+d+e)(a+¬c+¬e) • Reduction from SAT (See § 13. 3. 1). NP-Completeness 27

Map CNF-SAT to 3 SAT The SAT problem is still NP-complete even if it is in CNF and every clause has just 3 literals (a variable or its negation). 3 CNF-SAT • • • Must show we can map general form to restricted form. Map one clause at a time. If clause has a single variable a, map as (a+a+a) If clause has two terms (a+b) we map as (a+b+b) If the clause has three terms, we directly map If the clause has k terms we introduce additional variables which we’ll label as b 1…bk-3. (a 1+a 2+a 3+. . . +ak) = (a 1+a 2+b 1)(¬b 1+a 3+b 2)(¬b 2+a 4+b 3). . (¬bk-3+ak-1+ak) So – we have proven that 3 SAT is as difficult as CNF-SAT as we can solve any CNF-SAT problem by converting it to a 3 SAT problem NP-Completeness 28

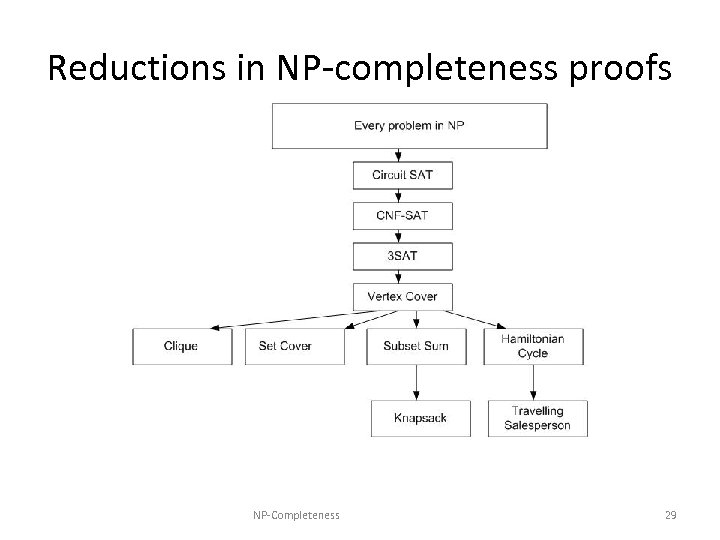Reductions in NP-completeness proofs NP-Completeness 29

Vertex Cover: subset of vertices which touch every edge • A vertex cover of graph G=(V, E) is a subset W of V, such that, for every edge (a, b) in E, a is in W or b is in W. • VERTEX-COVER: Given an graph G and an integer K, is does G have a vertex cover of size at most K? VERTEX-COVER is in NP: Non-deterministically choose a subset W of size K and check that every edge is covered by W. Notice how 3 SAT makes mapping easier as few cases! NP-Completeness 30

Vertex-Cover is NP-complete A vertex cover of graph G=(V, E) is a subset W of V, such that, for every edge (a, b) in E, a is in W or b is in W. We say every edge is “covered” by the set. Reduce 3 SAT to VERTEX-COVER – DISSIMILAR PROBLEMS? Pretty complicated mapping. Let S be a Boolean formula in CNF with each clause having 3 literals. For each variable x, create nodes for x and ¬x, and connect these two. x ¬x For each clause (x+ ¬ y+z), create a triangle with a node representing each term of the clause and connect these three nodes. The fact that they t 1 are connected indicated they are from the same clause. t 2 t 3 NP-Completeness 31

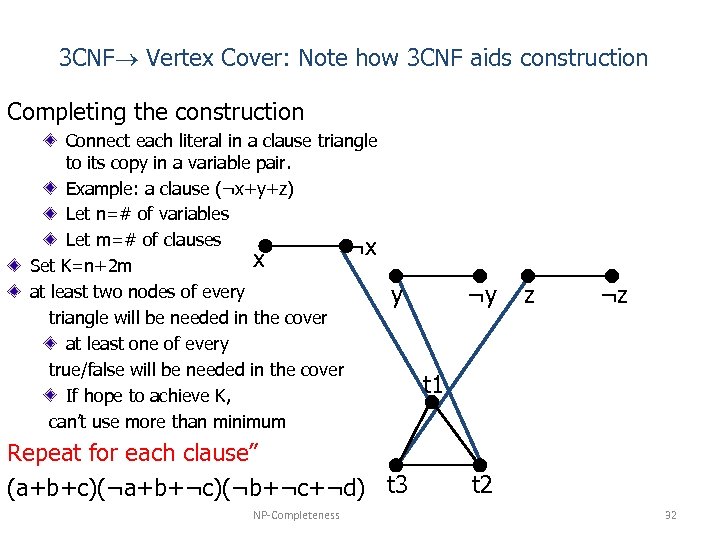3 CNF Vertex Cover: Note how 3 CNF aids construction Completing the construction Connect each literal in a clause triangle to its copy in a variable pair. Example: a clause (¬x+y+z) Let n=# of variables Let m=# of clauses ¬x x Set K=n+2 m at least two nodes of every triangle will be needed in the cover at least one of every true/false will be needed in the cover If hope to achieve K, can’t use more than minimum y Repeat for each clause” (a+b+c)(¬a+b+¬c)(¬b+¬c+¬d) t 3 NP-Completeness ¬y z ¬z t 1 t 2 32

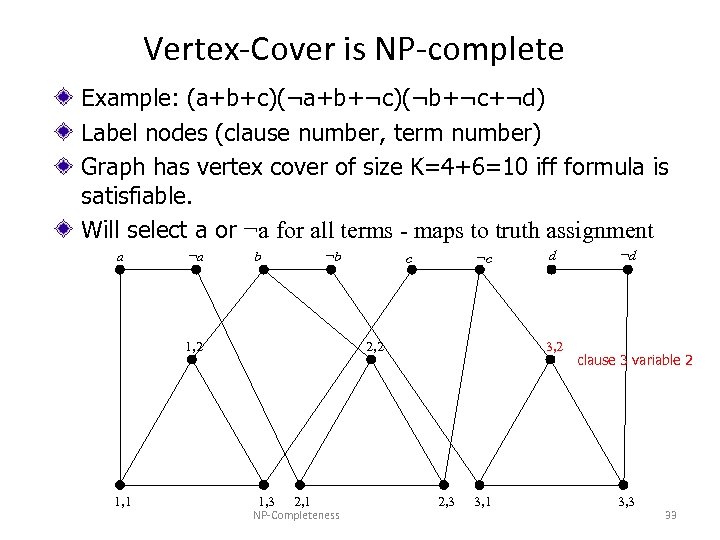Vertex-Cover is NP-complete Example: (a+b+c)(¬a+b+¬c)(¬b+¬c+¬d) Label nodes (clause number, term number) Graph has vertex cover of size K=4+6=10 iff formula is satisfiable. Will select a or ¬a for all terms - maps to truth assignment a ¬a b ¬b 1, 2 1, 1 c ¬c 2, 2 1, 3 2, 1 NP-Completeness d 3, 2 2, 3 3, 1 ¬d clause 3 variable 2 3, 3 33

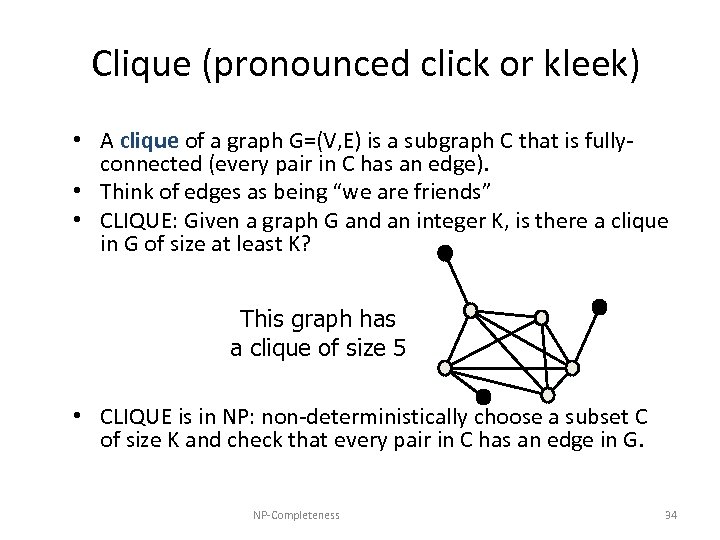Clique (pronounced click or kleek) • A clique of a graph G=(V, E) is a subgraph C that is fullyconnected (every pair in C has an edge). • Think of edges as being “we are friends” • CLIQUE: Given a graph G and an integer K, is there a clique in G of size at least K? This graph has a clique of size 5 • CLIQUE is in NP: non-deterministically choose a subset C of size K and check that every pair in C has an edge in G. NP-Completeness 34

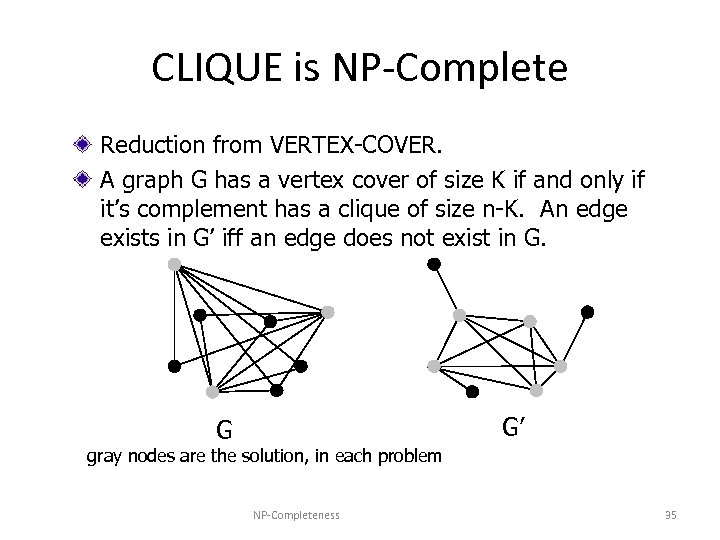CLIQUE is NP-Complete Reduction from VERTEX-COVER. A graph G has a vertex cover of size K if and only if it’s complement has a clique of size n-K. An edge exists in G’ iff an edge does not exist in G. G’ G gray nodes are the solution, in each problem NP-Completeness 35

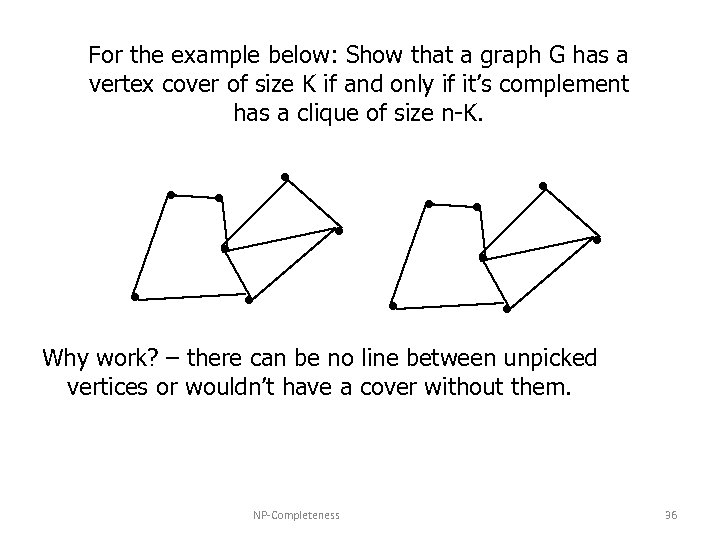For the example below: Show that a graph G has a vertex cover of size K if and only if it’s complement has a clique of size n-K. Why work? – there can be no line between unpicked vertices or wouldn’t have a cover without them. NP-Completeness 36

Some Other NPComplete Problems • SET-COVER: Given a collection of m sets, are there K of these sets whose union is the same as the whole collection of m sets? – NP-complete by reduction from VERTEX-COVER • SUBSET-SUM: Given a set of integers and a distinguished integer K, is there a subset of the integers that sums to K? – NP-complete by reduction from VERTEX-COVER NP-Completeness 37

Some Other NPComplete Problems • 0/1 Knapsack: Given a collection of items with weights and benefits, is there a subset of weight at most W and benefit at least K? (Recall we could do in pseudopolynomial time with dynamic programming) – NP-complete by reduction from SUBSET-SUM • Hamiltonian-Cycle: Given an graph G, is there a cycle in G that visits each vertex exactly once? – NP-complete by reduction from VERTEX-COVER • Traveling Salesperson Tour: Given a complete weighted graph G, is there a cycle that visits each vertex and has total cost at most K? – NP-complete by reduction from Hamiltonian-Cycle. NP-Completeness 38

Approximation Algorithms • While the complexity of finding exact solutions of all NPcomplete problems is the same up to polynomial factors, this elegant unified picture disappears rather dramatically when one considers approximate solutions. • Ex: while vertex cover and independent set are both the same problems for exact solutions, vertex cover has a simple factor 2 approximation (no worse that twice the best time) algorithm but independent set has been shown to be hard to approximate within any reasonable factor. • The lack of a unified picture makes the pursuit of understanding and classifying problems based on their approximability an intriguing one with diverse techniques used for studying different problems NP-Completeness 39

Backtracking and Branch and Bound (BAB) • Backtracking: consider all possibilities in logical order. Backtrack when illegal. • Example Knapsack: each item; take it or leave it. When backpack gets too full (no legal next choice), backtrack to earlier decision point. • In text, choice is made of most promising alternative, but all are tried eventually. • Consider list of alternatives: if recursion/stack, get depth first. If queue, get breadth first. NP-Completeness 40

BAB Don’t stop when one solution is found. Promising, but not guaranteed to be best. Keep going until best. Sometimes known as best-first strategy Keep a “best so far” solution Bound: If the “lower bound” on cost of a current solution is worse that the “best so far”, discard. • Lower bound MUST be less than or equal to the cost of a derived solution. If it is too high, you would throw out good choices. • • • NP-Completeness 41

Example: Pick a career with good $, little stress, little time. • Need to have a way of ordering so can try “best first”. Maybe try cheapest tuition first. Maybe know college generally produces better income. • Need to have a way of evaluating so can prune the search – as no potential for getting above best so far. Maybe know that taking over the family business would take 12 years but make $100 K, so opt not to work at Mc. Donalds as takes a long time. • Instead of depth first, or breadth first, gives best first. NP-Completeness 42

Branch and Bound(problem instance x) {F={(x, Ø)} //frontier set of subproblems b = (+ , Ø) // cost, config of best while (F Ø) { select from F the most promising (x, y) // y is certificate expand (x, y) yielding configs (xi, yi) for each new config (xi, yi) if solution found for (xi, yi) if cost, c, of solution < b then b = (c, (xi, yi)) else discard (xi, yi) if deadend or lb((xi, yi)) > b discard (xi, yi) else F = F {(xi, yi)} } return b } NP-Completeness 43

Concerns • space is an issue if all possible intermediate states are stored. • Iterative deepening – cost is only height of tree, not breadth! NP-Completeness 44

Approximation Ratios • Optimization Problems – We have some problem instance x that has many feasible “solutions”. – We are trying to minimize (or maximize) some cost function c(S) for a “solution” S to x. For example, • Finding a minimum spanning tree of a graph • Finding a smallest vertex cover of a graph • Finding a smallest traveling salesperson tour in a graph • An approximation produces a solution T – T is a k-approximation to the optimal solution OPT if c(T)/c(OPT) < k (assuming a min. prob. ; a maximization approximation would be the reverse) NP-Completeness 45

Polynomial-Time Approximation Schemes • problem has polynomial-time approximation scheme (PTAS) if it has a polynomial-time (1+ )-approximation algorithm, for any fixed >0 ( can appear in the running time). You control how far from optimal you are. • Needs to be rescalable: you have an equivalent problem by scaling the cost function. • 0/1 Knapsack has a PTAS, as we can just adjust the cost function (recall our dynamic programming problem was polynomial in total cost). Why can’t you scale the cost way down? What happens? (must be integer, so lose accuracy) • Has a running time that is O(n 3/ ). Please see § 13. 4. 1 in Goodrich-Tamassia for details. NP-Completeness 46

Vertex Cover • A vertex cover of graph G=(V, E) is a subset W of V, such that, for every (a, b) in E, a is in W or b is in W. • OPT-VERTEX-COVER: Given an graph G, find a vertex cover of G with smallest size. • Even given the size, it is tough! • OPT-VERTEX-COVER is NP-hard. NP-Completeness 47

A 2 -Approximation for Vertex Cover • Every chosen edge e has both ends in C • But e must be covered by an optimal cover; hence, one end of e must be in OPT • Thus, there is at most twice as many vertices in C as in OPT. • That is, C is a 2 -approx. of OPT • Running time: O(m) NP-Completeness Algorithm Vertex. Cover. Approx(G) Input graph G Output a vertex cover C for G C empty set H G while H has edges e H. remove. Edge(H. an. Edge()) v H. origin(e) w H. destination(e) C. add(v) C. add(w) for each f incident to v or w H. remove. Edge(f) return C 48

Simple solution • It is simple, but not stupid. Many seemingly smarter heuristics can give a far worse performance, in the worst case. • It is easy to complicate heuristics by adding more special cases or details. For example, if you just picked the edge whose endpoints had highest degree, it doesn’t improve the worst case. It just makes it harder to analyze. NP-Completeness 49

This seems like overkill, but • Why not just select one of the endpoints? Can get bad results (not abide by bound). Note what would happen if you picked the outside point for each edge. You would be far greater than a two approximation NP-Completeness 50

What if you picked the vertex with greatest degree? • Doesn’t always work either. In the case of ties (or near ties), you can get an approximation which is O(log n) times optimal (which isn’t a constant) NP-Completeness 51

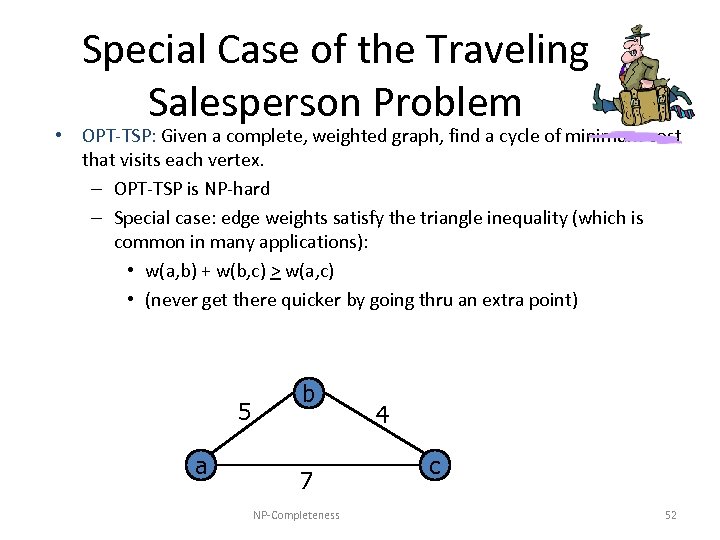Special Case of the Traveling Salesperson Problem • OPT-TSP: Given a complete, weighted graph, find a cycle of minimum cost that visits each vertex. – OPT-TSP is NP-hard – Special case: edge weights satisfy the triangle inequality (which is common in many applications): • w(a, b) + w(b, c) > w(a, c) • (never get there quicker by going thru an extra point) 5 a b 7 NP-Completeness 4 c 52

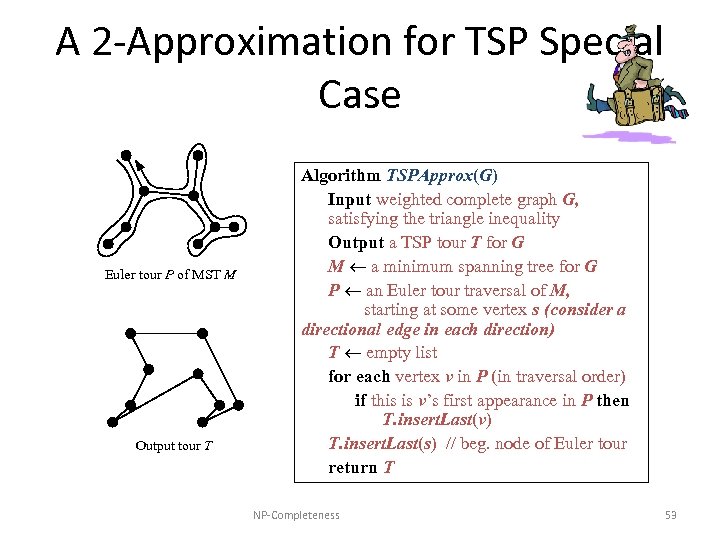A 2 -Approximation for TSP Special Case Euler tour P of MST M Output tour T Algorithm TSPApprox(G) Input weighted complete graph G, satisfying the triangle inequality Output a TSP tour T for G M a minimum spanning tree for G P an Euler tour traversal of M, starting at some vertex s (consider a directional edge in each direction) T empty list for each vertex v in P (in traversal order) if this is v’s first appearance in P then T. insert. Last(v) T. insert. Last(s) // beg. node of Euler tour return T NP-Completeness 53

Note This may produce a solution which crosses itself Try it with these points: NP-Completeness 54

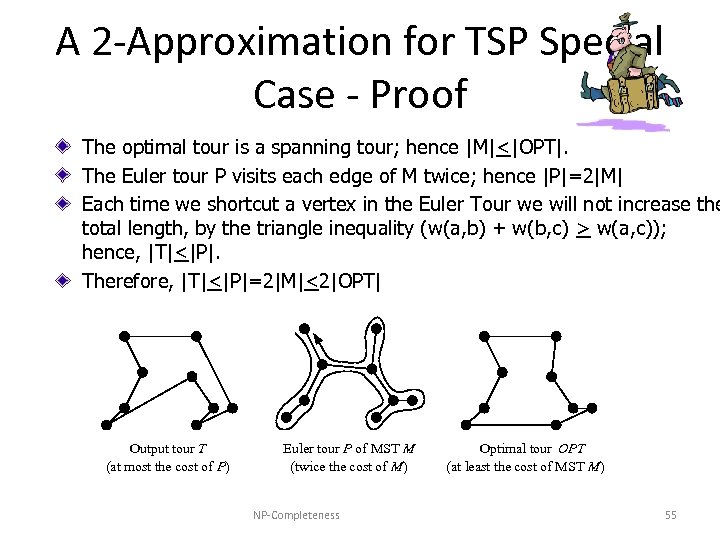A 2 -Approximation for TSP Special Case - Proof The optimal tour is a spanning tour; hence |M|<|OPT|. The Euler tour P visits each edge of M twice; hence |P|=2|M| Each time we shortcut a vertex in the Euler Tour we will not increase the total length, by the triangle inequality (w(a, b) + w(b, c) > w(a, c)); hence, |T|<|P|. Therefore, |T|<|P|=2|M|<2|OPT| Output tour T (at most the cost of P) Euler tour P of MST M (twice the cost of M) NP-Completeness Optimal tour OPT (at least the cost of MST M) 55

TSP Approximation • Is there any way to do a Monte Carlo approach? • Lots of work. Could use a least squares estimate. NP-Completeness 56

Set Cover • Example: need set of skills to solve a problem and want to hire fewest people. • OPT-SET-COVER: Given a collection, F, of m sets, find the smallest number of them whose union is the same as the whole collection of m sets? – OPT-SET-COVER is NP-hard • Greedy approach produces an O(log n)-approximation algorithm. See § 13. 4. 4 for details. NP-Completeness Algorithm Set. Cover. Approx(G) Input a collection of sets F={S 1…Sm} Output a subcollection C with same union F {S 1, S 2, …, Sm} C empty set U union of S 1…Sm while U is not empty Si set in F with most elements in U F. remove(Si) C. add(Si) Remove all elements in Si from U return C 57

Show Greedy Set Cover is a polynomial time p(n) approximation, where p(n) = H(max|S|) What is an hamonic number and how is it approviated? Euler proved: H(d) = (i=1. . d) 1/i = ln(d) = O(log d) NP-Completeness 58

Amortized Methods Helps us not to be misled by some cases being really bad • We assign 1 to each set selected by our approximation algorithm. • We distribute this cost over elements selected for the first time – and then use these costs to derive the relationship between the size of our cover C and the optimal over C*. • Fiddle with numbers to try to get a comparison between C and C*. • We pay 1 for each set chosen, so each of the k uncovered elements is charged 1/k. • Let Si denote the ith subset selected. • Given this assignment – consider the sum of all values in a set (not just new ones). What is bound? NP-Completeness 59

If x is covered for the first time by Si, then cx = 1/|(Si – (S 1 + S 2 +. . . Si-1))| Since each element of C is cost 1 |C| = cx Now, if we were willing to pay for every element each time it occurred in a set of the optimal cover, the cost assigned to the optimal cover C* (S in C*) (x in S) cx Since each x is in one C* (and some occur in several), But we don’t know anything about their repetition, so we just count them all (S in C*) (x in S) cx (each x) cx = |C| (as you might be counting some more than once) NP-Completeness 60

• Assume (for a minute) (x in S) cx H(|S|) = O(log |S|) (Where (H(|S|) is the harmonic number) Then |C| (S in C*) (x in S) cx = (S in C*) H(|S|) C* H(max |Si|) = C*log|S| (so our bound isn’t more than a factor of log |S| too much) NP-Completeness 61

Show (x in S) cx H(|S|) (if we added up all the elements in S, not just the ones we are covering now) • Order elements of S by order it is added to C. • The best thing that can happen is that all the elements in S are covered at once, so the total is 1. The worst thing that can happen is that each is uncovered by a different set. • If |S| = q, then the first thing added (because of another Si) must have no more cost that 1/q as otherwise S would have been selected not Si. • Similarly the next x added must have no more cost than 1/(q-1) • You add these all up and you get H(|S|) NP-Completeness 62

Show (x in S) cx H(|S|) (Formally) • Consider each Si in the order it is added to C. • Let ui = number of elements needing to be covered after Si has been selected • ui =|(S – (S 1 + S 2 +. . . Si))| • Thus ui-1 –ui elements are covered for the first time by Si. NP-Completeness 63

(x in S) cx = (ui-1 –ui) 1/|(Si – (S 1 + S 2 +. . . Si-1))| but |(Si – (S 1 + S 2 +. . . Si-1))| |(S – (S 1 + S 2 +. . . Si-1))| = ui-1 (x in S) cx (i=1. . k) (ui-1 –ui) 1/ui-1 but we can rewrite a product as a sum for example 4 z = (i=1. . 4) z (z is constant with respect to i) Thus (ui-1 –ui) 1/ui-1 = (j=ui+1, ui-1) 1/ui-1 (remember ui < ui-1) so (i=1. . k) (ui-1 –ui) 1/ui-1 = (i=1. . k) (j=ui+1, ui-1) 1/ui-1 (i=1. . k) (j=ui+1, ui-1)1/j as j ui-1 NP-Completeness 64

(i=1. . k) (j=ui+1, ui-1)1/j = (i=1. . k) ( (j=1, ui-1)1/j - (j=1, ui))1/j) = (i=1. . k) H(ui-1 ) – H(ui) = H(u 0) – H(uk) (because sum telescopes) but u 0 = |S| and uk =0 = H(|S|) (which is what we wanted to prove) NP-Completeness 65