Chapter 13 Investor Behavior and Capital Market Efficiency

13. 1 Competition and Capital Markets (cont'd) • Profiting from Non-Zero Alpha Stocks § Investors can improve the performance of their portfolios by buying stocks with positive alphas and by selling stocks with negative alphas. 10 -2

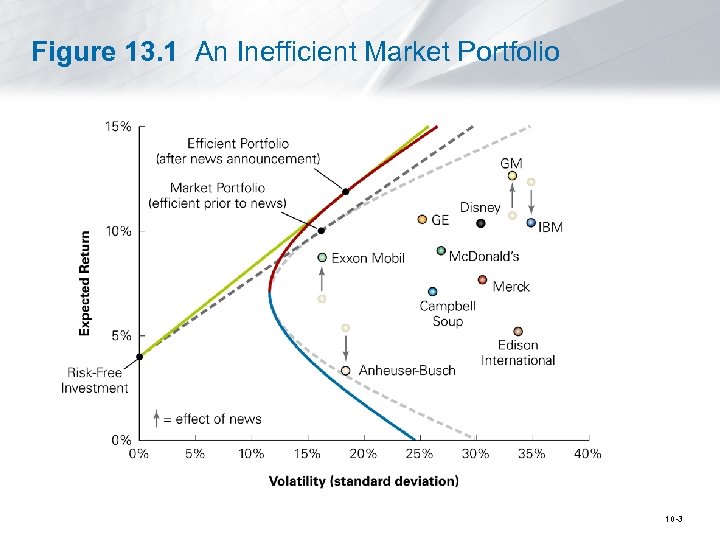
Figure 13. 1 An Inefficient Market Portfolio 10 -3

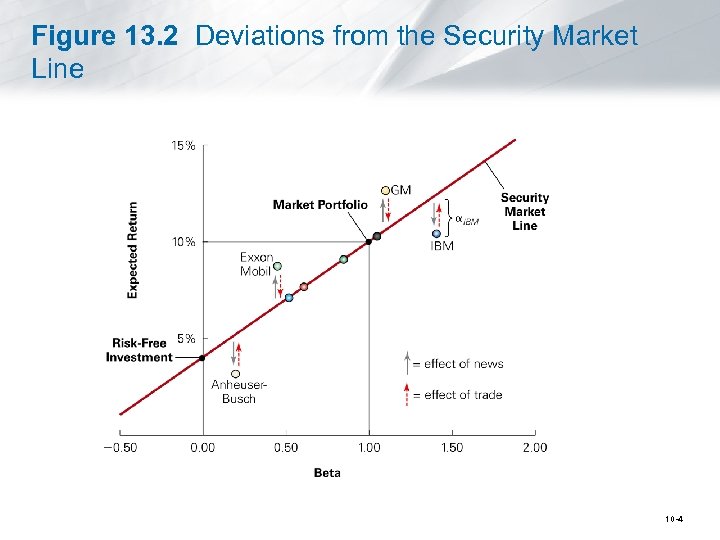
Figure 13. 2 Deviations from the Security Market Line 10 -4

13. 1 Competition and Capital Markets • Identifying a Stock’s Alpha § To improve the performance of their portfolios, investors will compare the expected return of a security with its required return from the security market line. 10 -5

Alpha The difference between a stock’s expected (or actual) return and its actual required return according to the security market line (the CAPM model) is called the stock’s alpha. § When the market portfolio is efficient, all stocks are on the security market line and have an alpha of zero. 10 -6

Textbook Example 13. 1 10 -7

13. 2 Information and Rational Expectations (cont’d) • Rational Expectations § All investors correctly interpret and use their own information, as well as information that can be inferred from market prices or the trades of others. § Regardless of how much information an investor has access to, he can guarantee himself an alpha of zero by holding the market portfolio. 10 -8

13. 2 Information and Rational Expectations (cont’d) • Because the average portfolio of all investors is the market portfolio, the average alpha of all investors is zero. • If no investor earns a negative alpha, then no investor can earn a positive alpha, and the market portfolio must be efficient. 10 -9

13. 2 Information and Rational Expectations (cont’d) • The market portfolio can be inefficient only if a significant number of investors either: § Misinterpret information and believe they are earning a positive alpha when they are actually earning a negative alpha, or § Care about aspects of their portfolios other than expected return and volatility, and so are willing to hold inefficient portfolios of securities. 10 -10

13. 3 The Behavior of Individual Investors Behavioral explanations for why investors do not invest in the market portfolio • Underdiversification and Portfolio Biases § There is much evidence that individual investors fail to diversify their portfolios adequately. § Familiarity Bias • Investors favor investments in companies they are familiar with § Relative Wealth Concerns • Investors care more about the performance of their portfolios relative to their peers. 10 -11

13. 3 The Behavior of Individual Investors (cont’d) • Excessive Trading and Overconfidence § According to the CAPM, investors should hold risk-free assets in combination with the market portfolio of all risky securities. § In reality, a tremendous amount of trading occurs each day. 10 -12

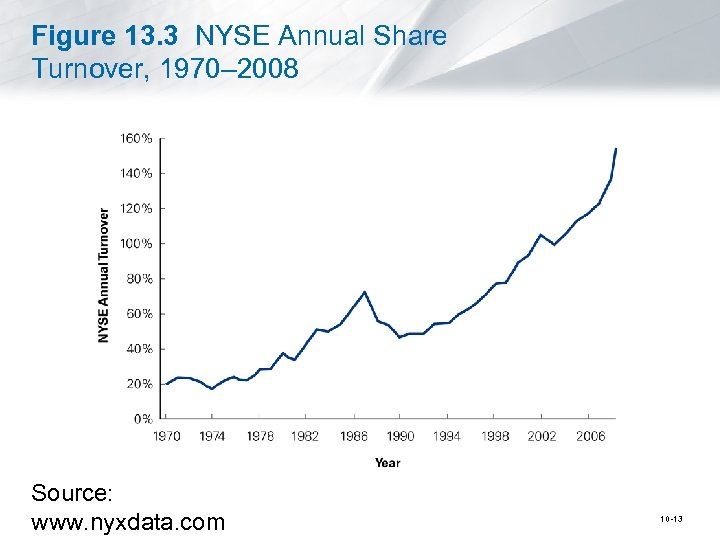
Figure 13. 3 NYSE Annual Share Turnover, 1970– 2008 Source: www. nyxdata. com 10 -13

13. 3 The Behavior of Individual Investors (cont’d) • Excessive Trading and Overconfidence § Overconfidence Bias • Investors believe they can pick winners and losers when, in fact, they cannot; this leads them to trade too much. § Sensation Seeking • An individual’s desire for novel and intense risk-taking experiences. 10 -14

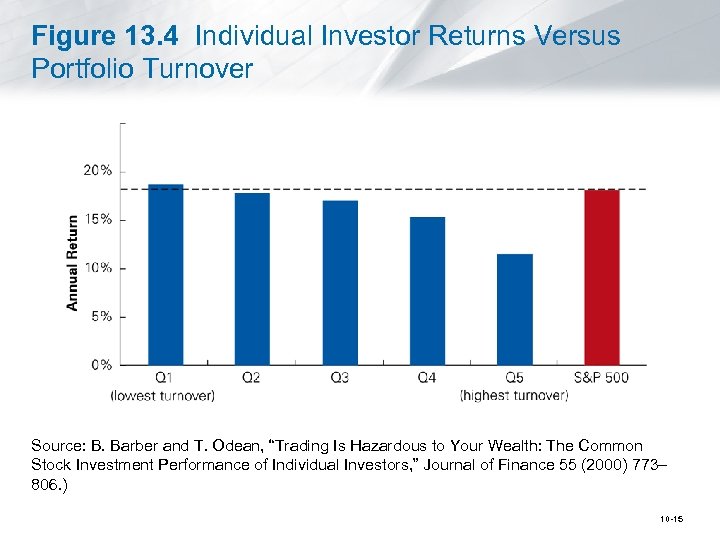
Figure 13. 4 Individual Investor Returns Versus Portfolio Turnover Source: B. Barber and T. Odean, “Trading Is Hazardous to Your Wealth: The Common Stock Investment Performance of Individual Investors, ” Journal of Finance 55 (2000) 773– 806. ) 10 -15

13. 3 The Behavior of Individual Investors (cont’d) • Individual Behavior and Market Prices § If individuals depart from the CAPM in random ways, then these departures will tend to cancel out. § Individuals will hold the market portfolio in aggregate, and there will be no effect on market prices or returns. 10 -16

13. 4 Systematic Trading Biases • Hanging on to Losers and the Disposition Effect § Disposition Effect • When an investor holds on to stocks that have lost their value and sell stocks that have risen in value since the time of purchase. • Investor Attention, Mood, and Experience § Studies show that individuals are more likely to buy stocks that have recently been in the news, engaged in advertising, experienced exceptionally high trading volume, or have had extreme returns. § Sunshine generally has a positive effect on mood, and studies have found that stock returns tend to be higher when it is a sunny day at the location of the stock exchange. 10 -17

13. 4 Systematic Trading Biases (cont’d) • Investor Attention, Mood, and Experience § Investors appear to put too much weight on their own experience rather than considering all the historical evidence. § As a result, people who grew up and lived during a time of high stock returns are more likely to invest in stocks than people who experienced times when stocks performed poorly. 10 -18

13. 5 The Efficiency of the Market Portfolio • If the market portfolio is efficient, securities should not have alphas that are significantly different from zero. § For most stocks the standard errors of the alpha estimates are large, so it is impossible to conclude that the alphas are statistically different from zero. § However, it is not difficult to find individual stocks that, in the past, have not plotted on the SML. 10 -19

13. 4 Systematic Trading Biases (cont’d) • Herd Behavior § When investors make similar trading errors because they are actively trying to follow each other’s behavior • Informational Cascade Effects § Where traders ignore their own information hoping to profit from the information of others 10 -20

13. 4 Systematic Trading Biases (cont’d) • Implications of Behavioral Biases § If individual investors are engaging in strategies that earn negative alphas, it may be possible for more sophisticated investors to take advantage of this behavior and earn positive alphas 10 -21

13. 5 The Efficiency of the Market Portfolio • Trading on News or Recommendations § Takeover Offers • If you could predict whether the firm would ultimately be acquired or not, you could earn profits trading on that information 10 -22

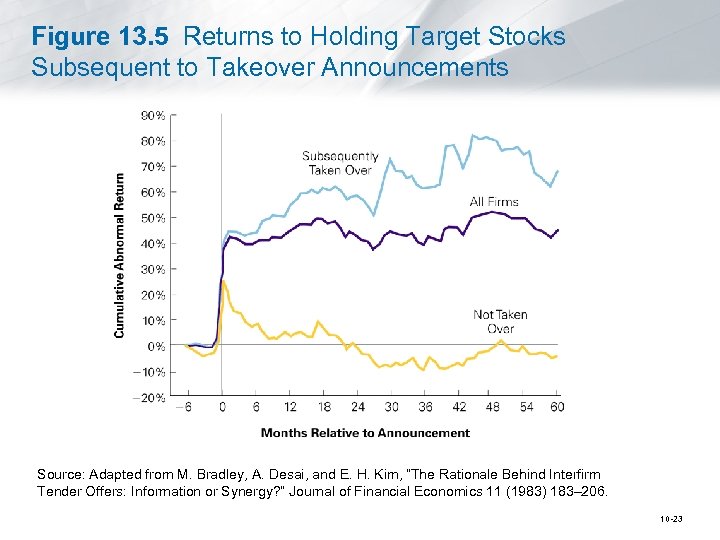
Figure 13. 5 Returns to Holding Target Stocks Subsequent to Takeover Announcements Source: Adapted from M. Bradley, A. Desai, and E. H. Kim, “The Rationale Behind Interfirm Tender Offers: Information or Synergy? ” Journal of Financial Economics 11 (1983) 183– 206. 10 -23

13. 5 The Efficiency of the Market Portfolio (cont’d) • Trading on News or Recommendations § Stock Recommendations • Jim Cramer makes numerous stock recommendations on his television show, Mad Money Ø Ø For stocks with news, it appears that the stock price correctly reflects this information the next day, and stays flat (relative to the market) subsequently On the other hand, for the stocks without news, there appears to be a significant jump in the stock price the next day, but the stock price then tends to fall relative to the market, generating a negative alpha, over the next several weeks 10 -24

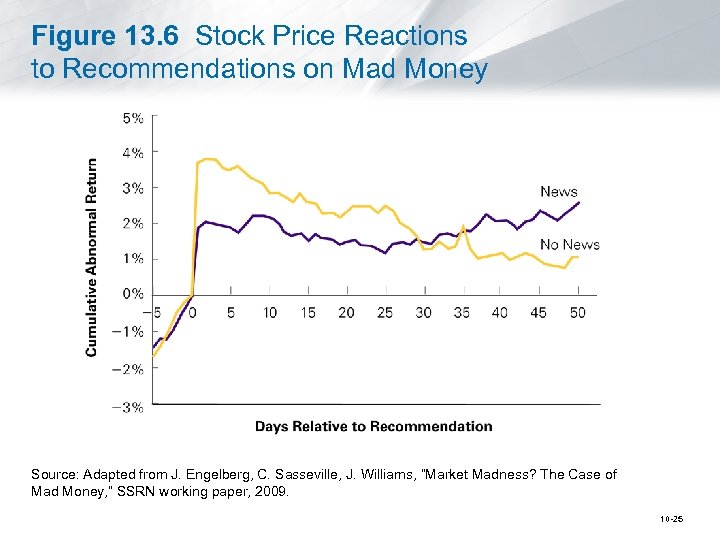
Figure 13. 6 Stock Price Reactions to Recommendations on Mad Money Source: Adapted from J. Engelberg, C. Sasseville, J. Williams, “Market Madness? The Case of Mad Money, ” SSRN working paper, 2009. 10 -25

13. 5 The Efficiency of the Market Portfolio (cont’d) • The Performance of Fund Managers § Numerous studies report that the actual returns to investors of the average mutual fund have a negative alpha § Superior past performance is not a good predictor of a fund’s future ability to outperform the market 10 -26

13. 6 Style-Based Anomalies and the Market Efficiency Debate • Researchers have studied whether portfolios of stocks plot on this line and have searched for portfolios that would be most likely to have nonzero alphas. § Researchers have identified a number of characteristics that can be used to pick portfolios that produce high average returns. 10 -27

The Size Effect • Size Effect § Stocks with lower market capitalizations have been found to have higher average returns. • Portfolios based on size were formed. • Portfolios consisting of small stocks had higher average excess returns than those consisting of large stocks. 10 -28

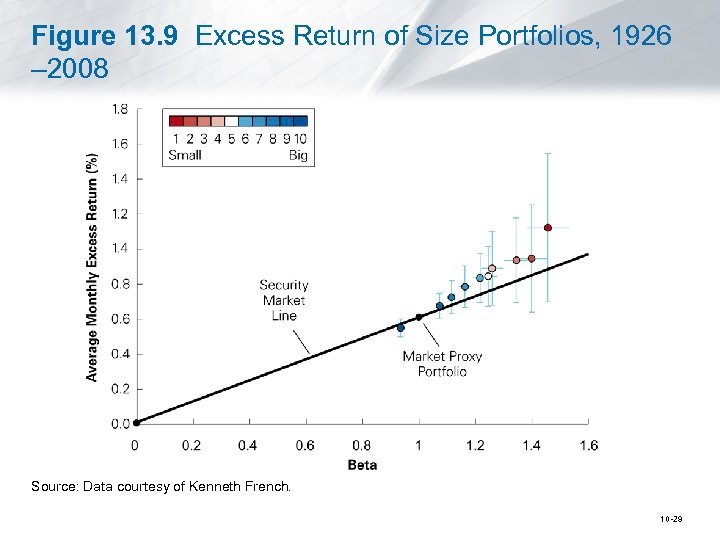
Figure 13. 9 Excess Return of Size Portfolios, 1926 – 2008 Source: Data courtesy of Kenneth French. 10 -29

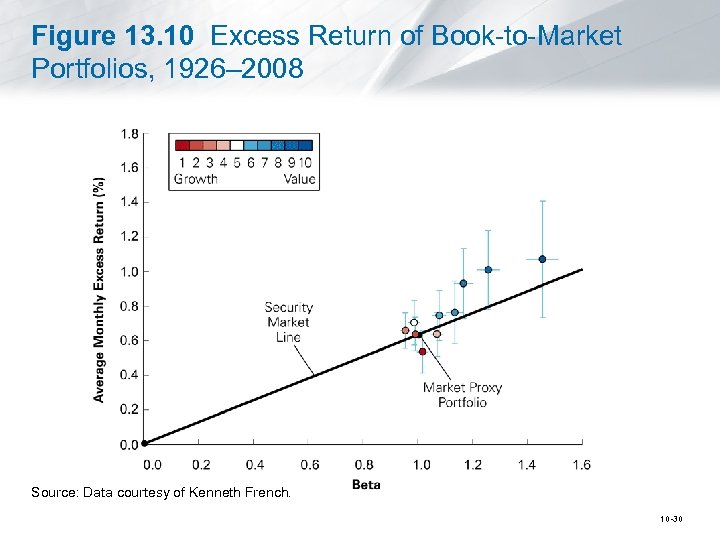
Figure 13. 10 Excess Return of Book-to-Market Portfolios, 1926– 2008 Source: Data courtesy of Kenneth French. 10 -30

The Size Effect (cont'd) • Data Snooping Bias § The idea that given enough characteristics, it will always be possible to find some characteristic that by pure chance happens to be correlated with the estimation error of a regression 10 -31

The Size Effect (cont'd) However, 1. The size effect did not seem to disappear 2. This is evidence against the efficiency of the market portfolio (Berk, 1995) 10 -32

Example • Problem § Suppose two firms, ABC and XYZ, are both expected to pay a dividend stream $2. 2 million per year in perpetuity. § ABC’s cost of capital is 12% per year and XYZ’s cost of capital is 16%. § Which firm has the higher market value? § Which firm has the higher expected return? 10 -33

Example • Problem § Now assume both stocks have the same estimated beta, either because of estimation error or because the market portfolio is not efficient. § Based on this beta, the CAPM would assign an expected return of 15% to both stocks. § Which firm has the higher alpha? § How do the market values of the firms relate to their alphas? 10 -34

Past Returns • Momentum Strategy § Buying stocks that have had past high returns (and shorting stocks that have had past low returns) • When the market portfolio is efficient, past returns should not predict alphas. • However, researchers found that the best performing stocks had positive alphas over the next six months. Ø This is evidence against the efficiency of the market portfolio. 10 -35

Implications of Positive Alphas • If the CAPM correctly computes the risk premium, an investment opportunity with a positive alpha is a positive-NPV investment opportunity, and investors should flock to invest in such strategies. 10 -36

Implications of Positive Alphas If the CAPM correctly computes risk premiums, but investors are ignoring opportunities to earn extra returns without bearing any extra risk, it is because 1. Investors are systematically ignoring positive-NPV investment opportunities. 2. The positive-alpha trading strategies contain risk that investors are unwilling to bear but the CAPM does not capture. This would suggest that the market portfolio is not efficient. 10 -37

Three main reasons why the CAPM fails • Proxy Error • Investors do not care about mean-variance • Non-tradeable Wealth 10 -38

13. 7 Multifactor Models of Risk • The expected return of any marketable security is: § When the market portfolio is not efficient, we have to find a method to identify an efficient portfolio before we can use the above equation. However, it is not actually necessary to identify the efficient portfolio itself. § All that is required is to identify a collection of portfolios from which the efficient portfolio can be constructed. 10 -39

Factor Portfolios • Assume that there are two portfolios that can be combined to form an efficient portfolio. 1. RF 1 and RF 2 are factor portfolios. The efficient portfolio consists of some (unknown) combination of these two factor portfolios, represented by portfolio weights x 1 and x 2: 2. To find βs of stock s, use multiple regression: If this two factors indeed capture all systematic risk that αs should equal zero. This means that if we form a portfolio where we buy stock s, short each of the factor portfolio according to its respective β, and invest in the risk free asset. We will a return which equals the risk free rate. 10 -40

Factor Portfolios § The result is the following two-factor model of expected returns: • Factor Beta § The sensitivity of the stock’s excess returns to the excess return of a factor portfolio. 10 -41

Using Factor Portfolios (cont'd) • Single-Factor versus Multi-Factor Model § A singe-factor model uses one portfolio while a multifactor model uses more than one portfolio in the model. § The CAPM is an example of a single-factor model while the Arbitrage Pricing Theory (APT) is an example of a multifactor model. 10 -42

Building a Multifactor Model • Given N factor portfolios with returns RF 1, . . . , RFN, the expected return of asset s is defined as: § β 1…. βN are the factor betas. 10 -43

Building a Multifactor Model (cont'd) • If all factor portfolios are self-financing then: 10 -44

Selecting the Portfolios • A trading strategy that each year buys a portfolio of small stocks and finances this position by short selling a portfolio of big stocks has historically produced positive risk-adjusted returns. § This self-financing portfolio is widely known as the small-minus-big (SMB) portfolio. 10 -45

Selecting the Portfolios (cont'd) • A trading strategy that each year buys an equallyweighted portfolio of stocks with a book-to-market ratio less than the 30 th percentile of NYSE firms and finances this position by short selling an equally-weighted portfolio of stocks with a book-to -market ratio greater than the 70 th percentile of NYSE stocks has historically produced positive risk-adjusted returns. § This self-financing portfolio is widely known as the high -minus-low (HML) portfolio. 10 -46

Selecting the Portfolios (cont'd) • Each year, after ranking stocks by their return over the last one year, a trading strategy that buys the top 30% of stocks and finances this position by short selling bottom 30% of stocks has historically produced positive riskadjusted returns. § This self-financing portfolio is widely known as the prior one-year momentum (PR 1 YR) portfolio. • This trading strategy requires holding the portfolio for a year and the process is repeated annually. 10 -47

Selecting the Portfolios (cont'd) • Currently the most popular choice for the multifactor model uses the excess return of the market, SMB, HML, and PR 1 YR portfolios. § Fama-French-Carhart (FFC) Factor Specifications 10 -48

Back to the basic Why is the inefficiency of the CAPM important? 1. For someone who wants to construct a portfolio 2. For a corporate manager trying to assess the NPV of a project. 10 -49

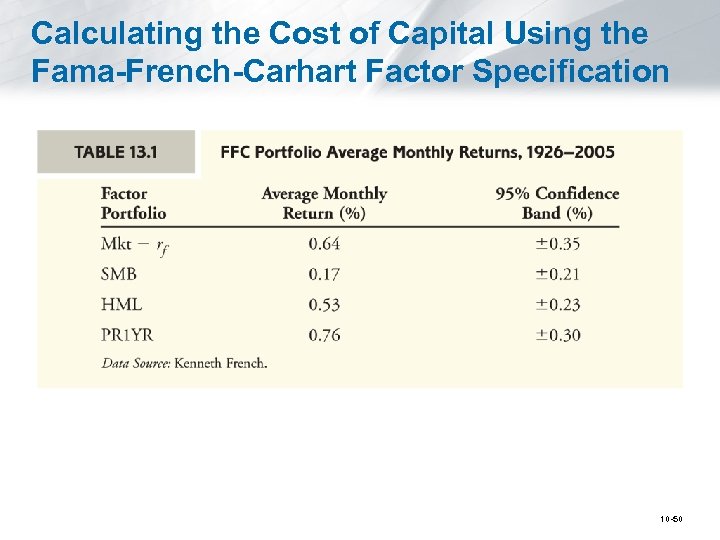
Calculating the Cost of Capital Using the Fama-French-Carhart Factor Specification 10 -50

Problem You are considering making an investment in a project in the semiconductor industry. § The project has the same level of non-diversifiable risk as investing in Intel stock. § Assume you have calculated the following factor betas for Intel stock: § Determine the cost of capital by using the FFC factor specification if the monthly risk-free rate is 0. 5%. 4 -factors. xls 10 -51

Calculating the Cost of Capital Using the Fama. French-Carhart Factor Specification (cont'd) • Although it is widely used in research to measure risk, there is much debate about whether the FFC factor specification is really a significant improvement over the CAPM. § One area where researchers have found that the FFC factor specification does appear to do better than the CAPM is measuring the risk of actively managed mutual funds. • Researchers have found that funds with high returns in the past have positive alphas under the CAPM. When the same tests were repeated using the FFC factor specification to compute alphas, no evidence was found that mutual funds with high past returns had future positive alphas. 10 -52

So, why is it hard to calculate cost of capital based on multi-factor models? • Calculating the cost of capital using the multifactor model relies on accurate estimates of risk premiums and betas. § Accurately estimating these quantities is difficult. Both risk premiums and betas may not remain stable over time because. . 1. Statistical errors – especially in multifactor models. 2. Economic reason – firms change over time 10 -53

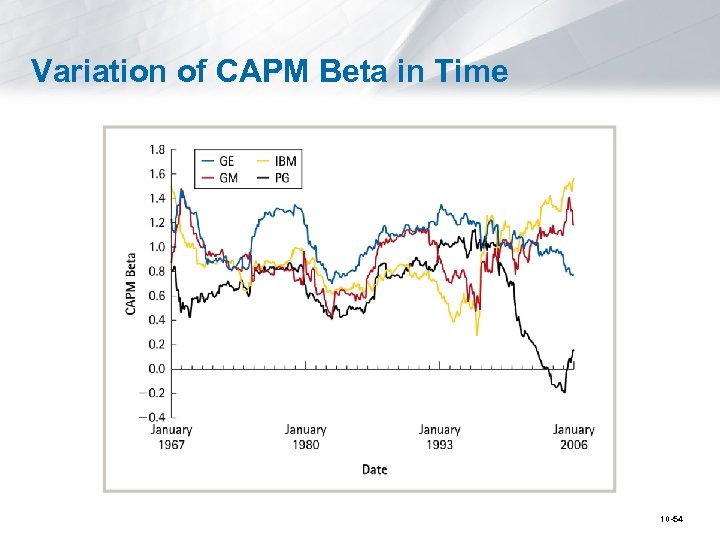
Variation of CAPM Beta in Time 10 -54