Chapter 12 Swaps I once had to explain

Chapter 12: Swaps I once had to explain to my father that the bank didn’t really make its money taking deposits and lending out money to poor folk so they could buy houses. I explained that the bank actually traded for a living. Stan Jonas Derivatives Strategy, April, 1998, p. 19 D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. Ch. 12: 1

Important Concepts in Chapter 12 n n The concept of a swap Different types of swaps, based on underlying currency, interest rate, or equity Pricing and valuation of swaps Strategies using swaps D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 2

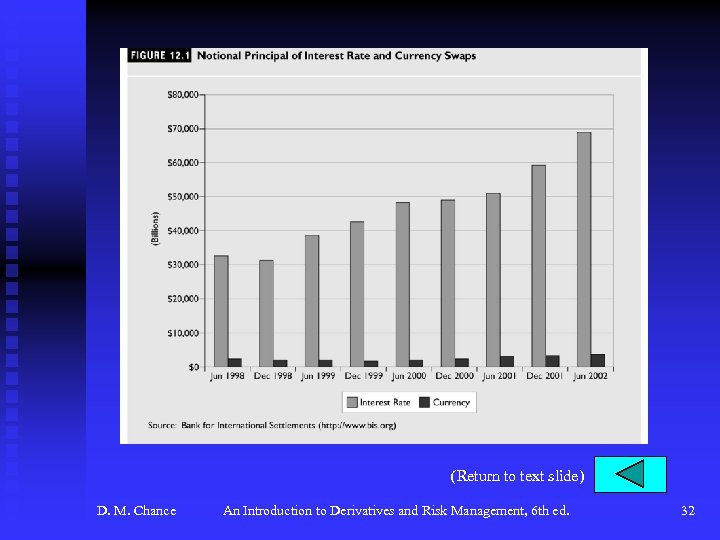
n n Definition of a swap Four types of swaps u Currency u Interest rate u Equity u Commodity (not covered in this book) Characteristics of swaps u No cash up front u Notional principal u Settlement date, settlement period u Credit risk u Dealer market See Figure 12. 1, p. 426 for growth in world-wide notional principal D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 3

Interest Rate Swaps u The Structure of a Typical Interest Rate Swap F Example: On December 15 XYZ enters into $50 million NP swap with ABSwaps. Payments will be on 15 th of March, June, September, December for one year, based on LIBOR. XYZ will pay 7. 5% fixed and ABSwaps will pay LIBOR. Interest based on exact day count and 360 days (30 per month). In general the cash flow to the fixed payer will be D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 4

Interest Rate Swaps (continued) u The Structure of a Typical Interest Rate Swap (continued) F The payments in this swap are F Payments are netted. F See Figure 12. 2, p. 428 for payment pattern F See Table 12. 1, p. 429 for sample of payments afterthe-fact. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 5

Interest Rate Swaps (continued) u The Pricing and Valuation of Interest Rate Swaps F How is the fixed rate determined? F A digression on floating-rate securities. The price of a LIBOR zero coupon bond for maturity of ti days is • Starting at the maturity date and working back, we see that the price is par on each coupon date. See Figure 12. 3, p. 430. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 6

Interest Rate Swaps (continued) u The Pricing and Valuation of Interest Rate Swaps (continued) F By adding the notional principals at the end, we can separate the cash flow streams of an interest rate swap into those of a fixed-rate bond a floatingrate bond. F See Figure 12. 4, p. 431. F The value of a fixed-rate bond (q = days/360): D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 7

Interest Rate Swaps (continued) u The Pricing and Valuation of Interest Rate Swaps (continued) F The value of a floating-rate bond F At time t, between 0 and 1, F The value of the swap (pay fixed, receive floating) is, therefore, D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 8

Interest Rate Swaps (continued) u The Pricing and Valuation of Interest Rate Swaps (continued) F To price the swap at the start, set this value to zero and solve for R See Table 12. 2, p. 433 for an example. F Note how dealers quote as a spread over Treasury rate. F To value a swap during its life, simply find the difference between the present values of the two streams of payments. See Table 12. 3, p. 434. Market value reflects the economic value, is necessary for accounting, and gives an indication of the credit risk. F D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 9

Interest Rate Swaps (continued) u The Pricing and Valuation of Interest Rate Swaps (continued) F A basis swap is equivalent to the difference between two plain vanilla swaps based on different rates: • A swap to pay T-bill, receive fixed, plus • A swap to pay fixed, receive LIBOR, equals • A swap to pay T-bill, receive LIBOR, plus pay the difference between the LIBOR and T-bill fixed rates • See Tables 12. 4 and 12. 5, p. 436 for examples of pricing and valuation of a basis swap. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 10

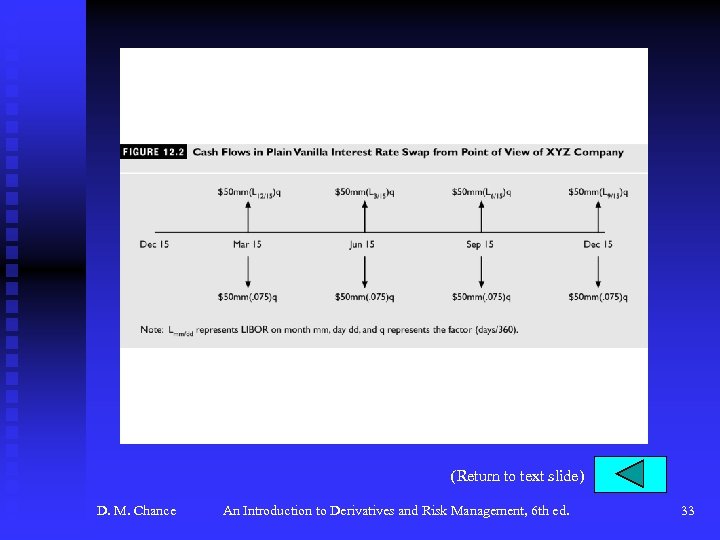
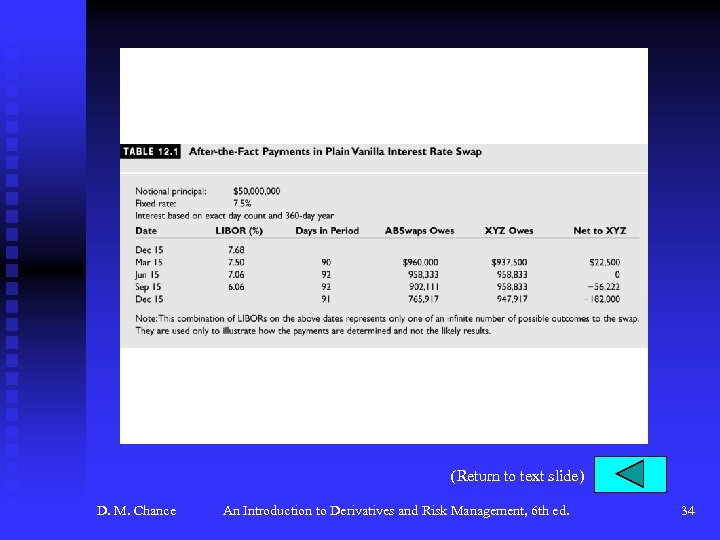
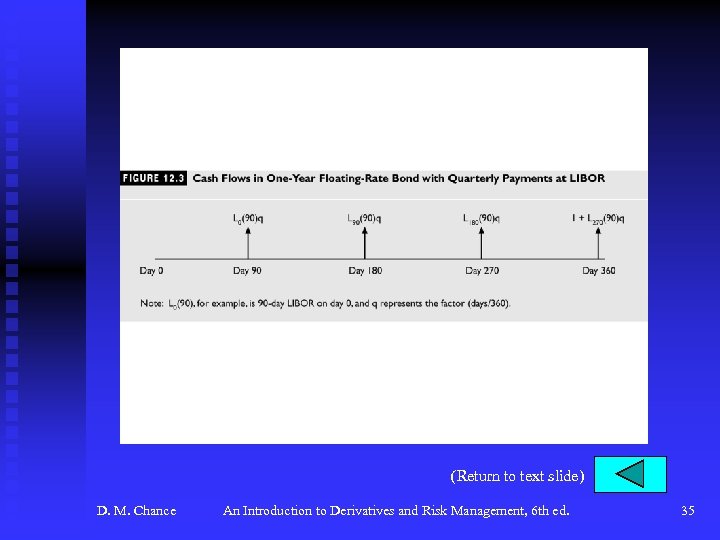
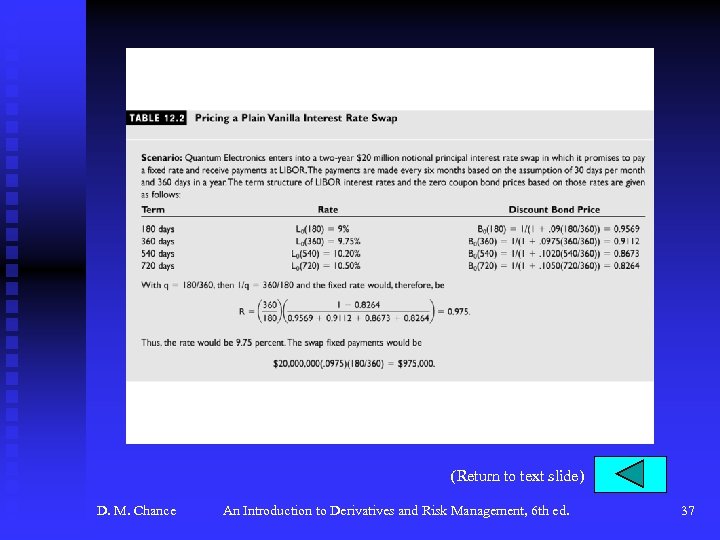
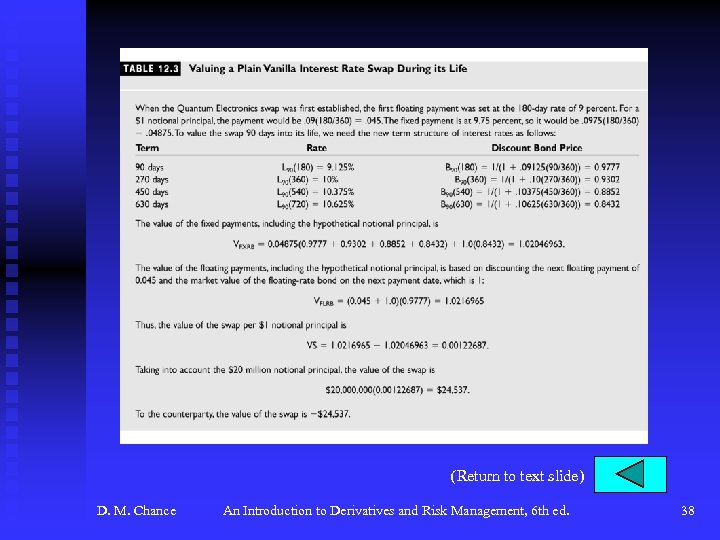
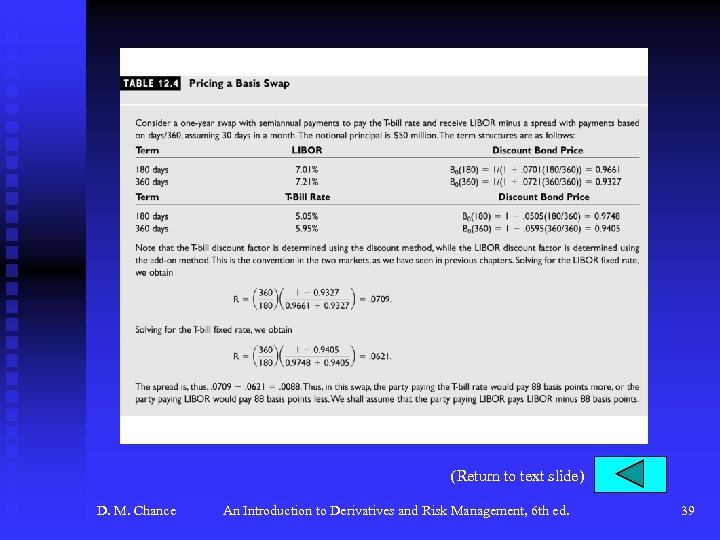
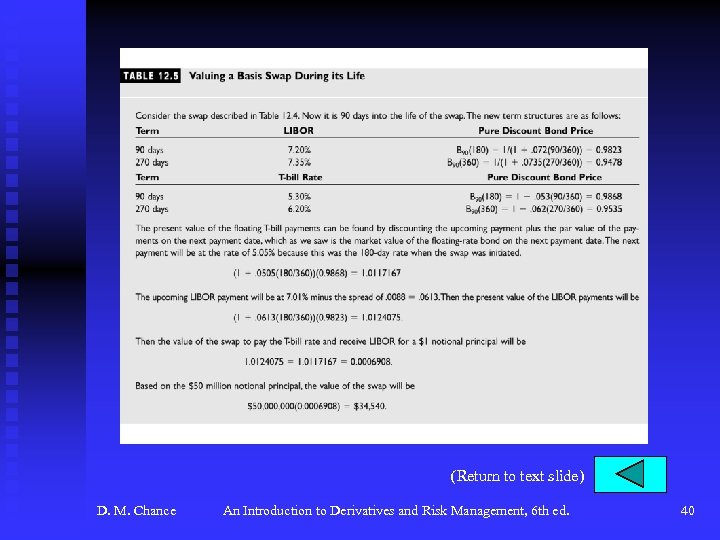
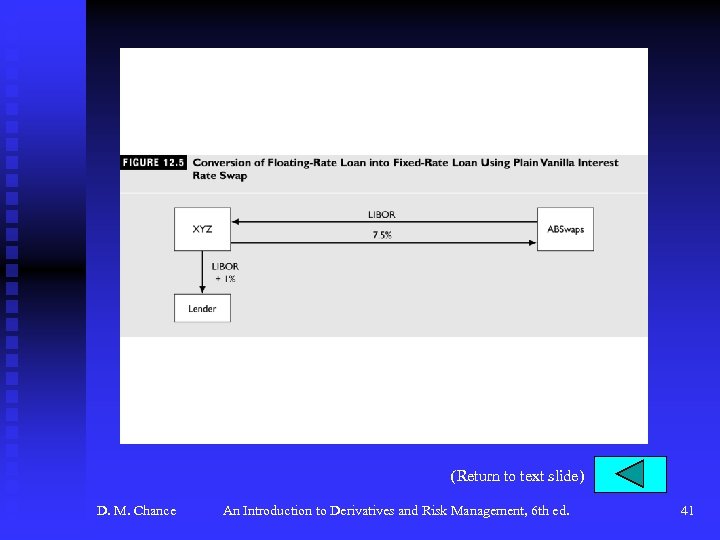
Interest Rate Swaps (continued) u Interest Rate Swap Strategies F See Figure 12. 5, p. 437 for example of converting floating-rate loan into fixed-rate loan F Other types of swaps • Index amortizing swaps • Diff swaps • Constant maturity swaps D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 11

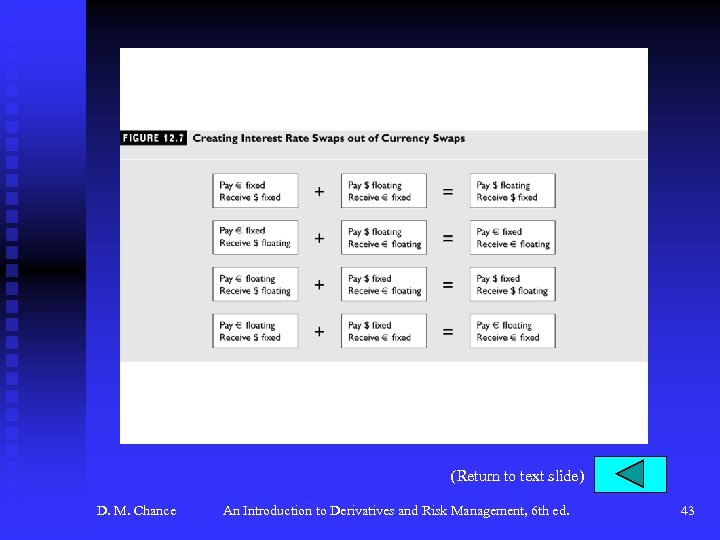
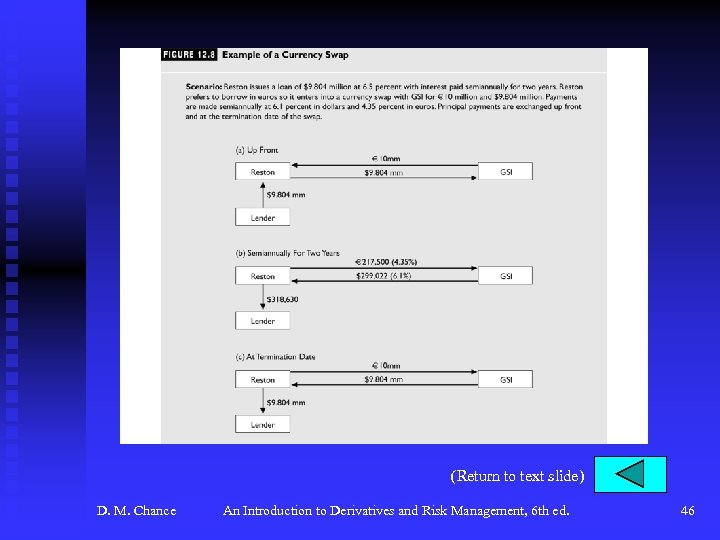
Currency Swaps u Example: Reston Technology enters into currency swap with GSI. Reston will pay euros at 4. 35% based on NP of € 10 million semiannually for two years. GSI will pay dollars at 6. 1% based on NP of $9. 804 million semiannually for two years. Notional principals will be exchanged. F See Figure 12. 6, p. 440. u Note the relationship between interest rate and currency swaps in Figure 12. 7, p. 441. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 12

Currency Swaps (continued) u Pricing and Valuation of Currency Swaps F Let dollar notional principal be NP$. Then euro notional principal is NP€ = 1/S 0 for every dollar notional principal. Here euro notional principal will be € 10 million. With S 0 = $0. 9804, NP$ = $9, 804, 000. F For fixed payments, we use the fixed rate on plain vanilla swaps in that currency, R$ or R€. F No pricing is required for the floating side of a currency swap. F See Table 12. 6, p. 443. F During the life of the swap, we value it by finding the difference in the present values of the two streams of payments, adjusting for the notional principals, and converting to a common currency. Assume new exchange rate is $0. 9790 three months later. F See Table 12. 7, p. 444 for calculations of values of streams of payments per unit notional principal. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 13

Currency Swaps (continued) u Pricing and Valuation of Currency Swaps (continued) F Dollars fixed for NP of $9. 804 million = $9, 804, 000(1. 01132335) = $9, 915, 014 F Dollars floating for NP of $9. 804 million = $9, 804, 000(1. 013115) = $9, 932, 579 F Euros fixed for NP of € 10 million = € 10, 000(1. 00883078) = € 10, 088, 308 F Euros floating for NP of € 10 million = € 10, 000(1. 0091157) = € 10, 091, 157 D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 14

Currency Swaps (continued) u Pricing and Valuation of Currency Swaps (continued) F Value of swap to pay € fixed, receive $ fixed • $9, 915, 014 - € 10, 088, 308($0. 9790/€) = $38, 560 F Value of swap to pay € fixed, receive $ floating • $9, 932, 579 - € 10, 088, 308($0. 9790/€) = $56, 125 F Value of swap to pay € floating, receive $ fixed • $9, 915, 014 - € 10, 091, 157($0. 9790/€) = $35, 771 F Value of swap to pay € floating, receive $ floating • $9, 932, 579 - € 10, 091, 157($0. 9790/€) = $53, 336 D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 15

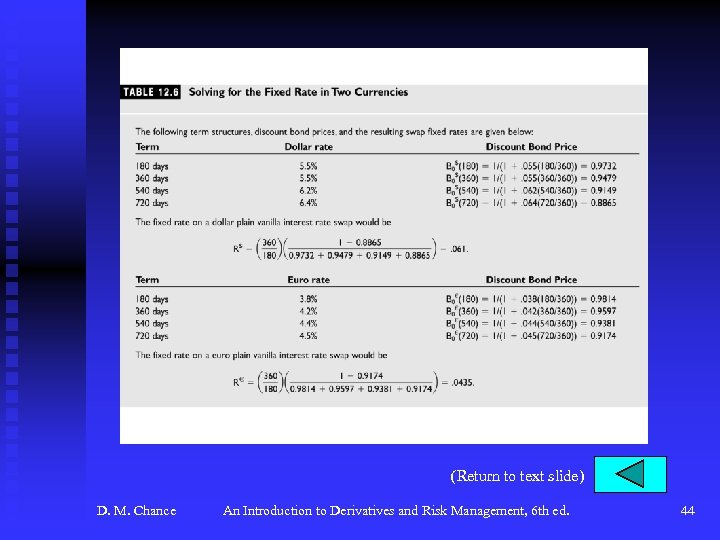
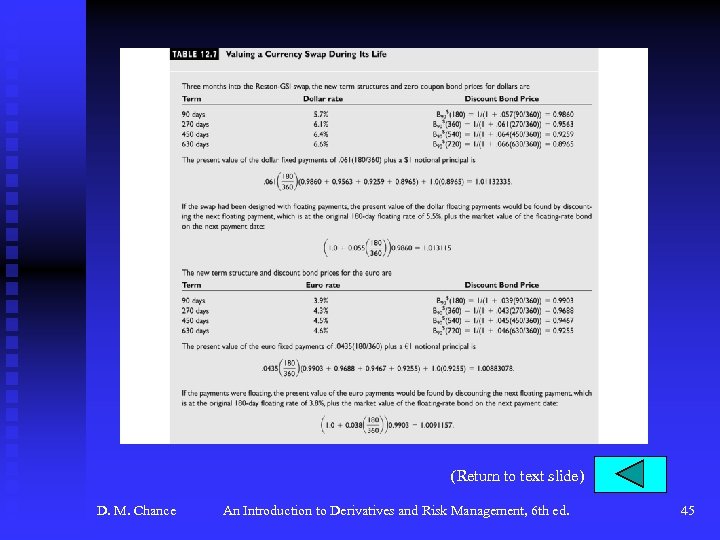
Currency Swaps (continued) u Currency Swap Strategies FA typical case is a firm borrowing in one currency and wanting to borrow in another. See Figure 12. 8, p. 448 for Reston-GSI example. Reston could get a better rate due to its familiarity to GSI and also due to credit risk. F Also a currency swap be used to convert a stream of foreign cash flows. This type of swap would probably have no exchange of notional principals. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 16

Equity Swaps u Characteristics F One party pays the return on an equity, the other pays fixed, floating, or the return on another equity F Rate of return is paid, so payment can be negative F Payment is not determined until end of period D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 17

Equity Swaps (continued) u The Structure of a Typical Equity Swap F Cash flow to party paying stock and receiving fixed F Example: IVM enters into a swap with FNS to pay S&P 500 Total Return and receive a fixed rate of 3. 45%. The index starts at 2710. 55. Payments every 90 days for one year. Net payment will be D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 18

Equity Swaps (continued) u The Structure of a Typical Equity Swap (continued) F The fixed payment will be • $25, 000(. 0345)(90/360) = $215, 625 F See Table 12. 8, p. 451 for example of payments. The first equity payment is F So D. M. Chance the first net payment is IVM pays $285, 657. An Introduction to Derivatives and Risk Management, 6 th ed. 19

Equity Swaps (continued) u The Structure of a Typical Equity Swap (continued) F If IVM had received floating, the payoff formula would be F If the swap were structured so that IVM pays the return on one stock index and receives the return on another, the payoff formula would be D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 20

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps F For a swap to pay fixed and receive equity, we replicate as follows: • Invest $1 in stock • Issue $1 face value loan with interest at rate R. Pay interest on each swap settlement date and repay principal at swap termination date. Interest based on q = days/360. • Example: Assume payments on days 180 and 360. – On day 180, stock worth S 180/S 0. Sell stock and withdraw S 180/S 0 - 1 – Owe interest of Rq – Overall cash flow is S 180/S 0 – 1 – Rq, which is equivalent to the first swap payment. $1 is left over. Reinvest in the stock. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 21

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F On day 360, stock is worth S 360/S 180. F Liquidate stock. Pay back loan of $1 and interest of Rq. F Overall cash flow is S 360/S 180 – 1 – Rq, which is equivalent to the second swap payment. F The value of the position is the value of the swap. In general for n payments, the value at the start is D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 22

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F Setting the value to zero and solving for R gives F which is the same as the fixed rate on an interest rate swap. See Table 12. 9, p. 453 for pricing the IVM swap. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 23

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F To value the swap at time t during its life, consider the party paying fixed and receiving equity. F To replicate the first payment, at time t • Purchase 1/S 0 shares at a cost of (1/S 0)St. Borrow $1 at rate R maturing at next payment date. • At the next payment date (assume day 90), shares are worth (1/S 0)S 90. Sell the stock, generating (1/S 0)S 90 – 1 (equivalent to the equity payment on the swap), plus $1 left over, which is reinvested in the stock. Pay the loan interest, Rq (which is equivalent to the fixed payment on the swap). • Do this for each payment on the swap. D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 24

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F The cost to do this strategy at time t is This is the value of the swap. See Table 12. 10, p. 454 for an example of the IVM swap. F To value the equity swap receiving floating and paying equity, note the equivalence to • A swap to pay equity and receive fixed, plus • A swap to pay fixed and receive floating. F So we can use what we already know. F D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 25

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F Using the new discount factors, the value of the fixed payments (plus hypothetical notional principal) is • . 0345(90/360)(0. 9971 + 0. 9877 + 0. 9778 + 0. 9677) + 1(0. 9677) = 1. 00159884 F The value of the floating payments (plus hypothetical notional principal) is • (1 +. 03(90/360))(0. 9971) = 1. 00457825 F The plain vanilla swap value is, thus, • 1. 00457825 – 1. 00159884 = -0. 00297941 F For a $25 million notional principal, • $25, 000(-0. 00297941) = -$74, 485 F So the value of the equity swap is (using -$227, 964, the value of the equity swap to pay fixed) • -$227, 964 - $74, 485 = -$302, 449 D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 26

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F For swaps to pay one equity and receive another, replicate by selling short one stock and buy the other. Each period withdraw the cash return, reinvesting $1. Cover short position by buying it back, and then sell short $1. So each period start with $1 long one stock and $1 short the other. F For the IVM swap, suppose we pay the S&P and receive NASDAQ, which starts at 2710. 55 and goes to 2739. 60. The value of the swap is D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 27

Equity Swaps (continued) u Pricing and Valuation of Equity Swaps (continued) F For $25 million notional principal, the value is • $25, 000(0. 03312974) = $828, 244 D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 28

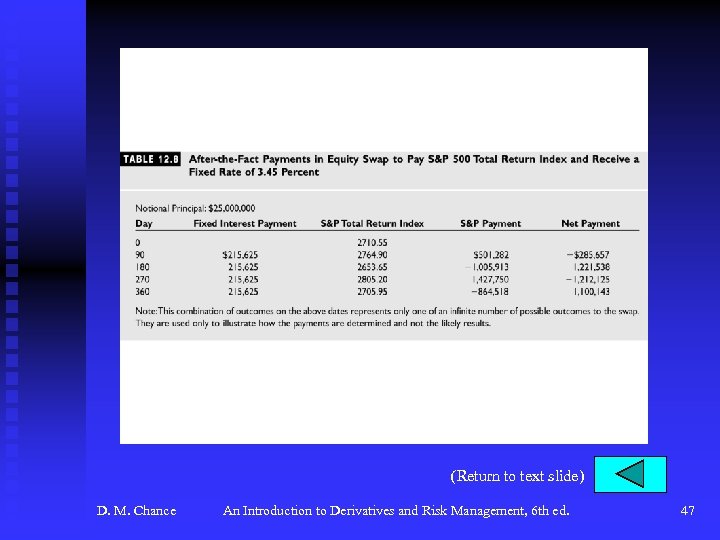
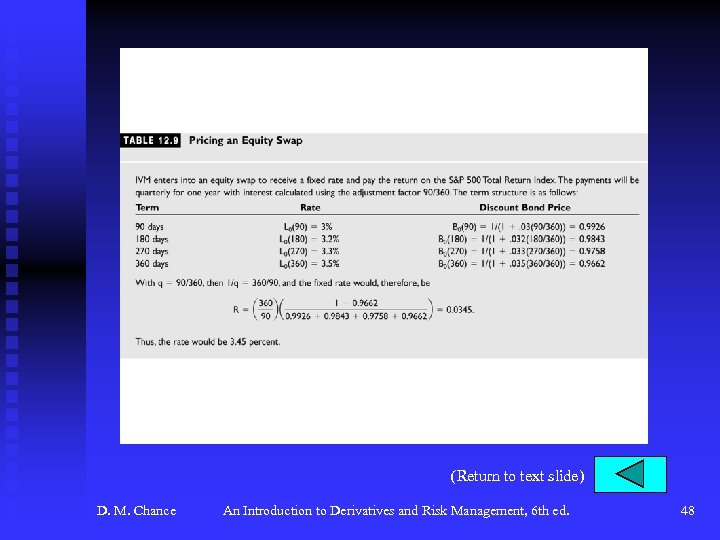
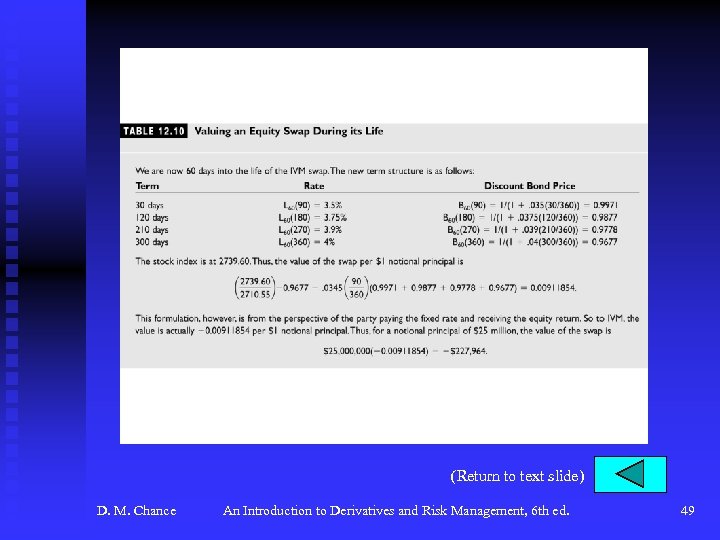
Equity Swaps (continued) u Equity Swap Strategies F Used to synthetically buy or sell stock F See Figure 12. 9, p. 456 for example. F Some risks • default • tracking error • cash flow shortages D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 29

Some Final Words About Swaps u Similarities to forwards and futures u Offsetting swaps F Go back to dealer F Offset with another counterparty F Forward contract or option on the swap D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 30

Summary D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 31

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 32

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 33

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 34

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 35

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 36

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 37

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 38

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 39

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 40

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 41

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 42

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 43

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 44

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 45

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 46

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 47

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 48

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 49

(Return to text slide) D. M. Chance An Introduction to Derivatives and Risk Management, 6 th ed. 50