Chapter 12 Risk and Refinements in Capital Budgeting

Learning Goals LG 1 Understand the importance of recognizing risk in the analysis of capital budgeting projects. LG 2 Discuss risk and cash inflows, scenario analysis, and simulation as behavioral approaches for dealing with risk. LG 3 Review the unique risks that multinational companies face. © 2012 Pearson Prentice Hall. All rights reserved. 2

Learning Goals (cont. ) LG 4 Describe the determination and use of risk-adjusted discount rates (RADRs), portfolio effects, and the practical aspects of RADRs. LG 5 Select the best of a group of unequal-lived, mutually exclusive projects using annualized net present values (ANPVs). LG 6 Explain the role of real options and the objective and procedures for selecting projects under capital rationing. © 2012 Pearson Prentice Hall. All rights reserved. 3

Introduction to Risk in Capital Budgeting • Thus far, we have assumed that all investment projects have the same level of risk as the firm. • In other words, we assumed that all projects are equally risky, and the acceptance of any project would not change the firm’s overall risk. • In actuality, these situations are rare—projects are not equally risky, and the acceptance of a project can affect the firm’s overall risk. © 2012 Pearson Prentice Hall. All rights reserved. 4

Table 12. 1 Cash Flows and NPVs for Bennett Company’s Projects © 2012 Pearson

Behavioral Approaches for Dealing with Risk: Risk and Cash Inflows • Behavioral approaches can be used to get a “feel” for the level of project risk, whereas other approaches try to quantify and measure project risk. • Risk (in capital budgeting) refers to the uncertainty surrounding the cash flows that a project will generate or, more formally, the degree of variability of cash flows. • In many projects, risk stems almost entirely from the cash flows that a project will generate several years in the future, because the initial investment is generally known with relative certainty. © 2012 Pearson Prentice Hall. All rights reserved. 6

Behavioral Approaches for Dealing with Risk: Risk and Cash Inflows (cont. ) Treadwell Tire Company, a tire retailer with a 10% cost of capital, is considering investing in either of two mutually exclusive projects, A and B. Each requires a $10, 000 initial investment, and both are expected to provide constant annual cash inflows over their 15 -year lives. For either project to be acceptable its NPV must be greater than zero. © 2012 Pearson Prentice Hall. All rights reserved. 7

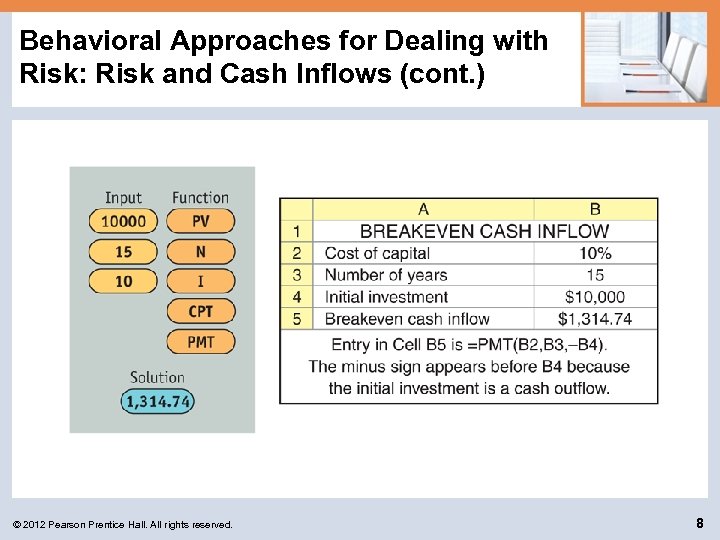
Behavioral Approaches for Dealing with Risk: Risk and Cash Inflows (cont. ) © 2012

Behavioral Approaches for Dealing with Risk: Scenario Analysis • Scenario analysis is a behavioral approach that uses several possible alternative outcomes (scenarios), to obtain a sense of the variability of returns, measured here by NPV. • In capital budgeting, one of the most common scenario approaches is to estimate the NPVs associated with pessimistic (worst), most likely (expected), and optimistic (best) estimates of cash inflow. • The range can be determined by subtracting the pessimistic-outcome NPV from the optimistic-outcome NPV. © 2012 Pearson Prentice Hall. All rights reserved. 9

Table 12. 2 Scenario Analysis of Treadwell’s Projects A and B © 2012 Pearson

Behavioral Approaches for Dealing with Risk: Simulation is a statistics-based behavioral approach that applies predetermined probability distributions and random numbers to estimate risky outcomes. © 2012 Pearson Prentice Hall. All rights reserved. 11

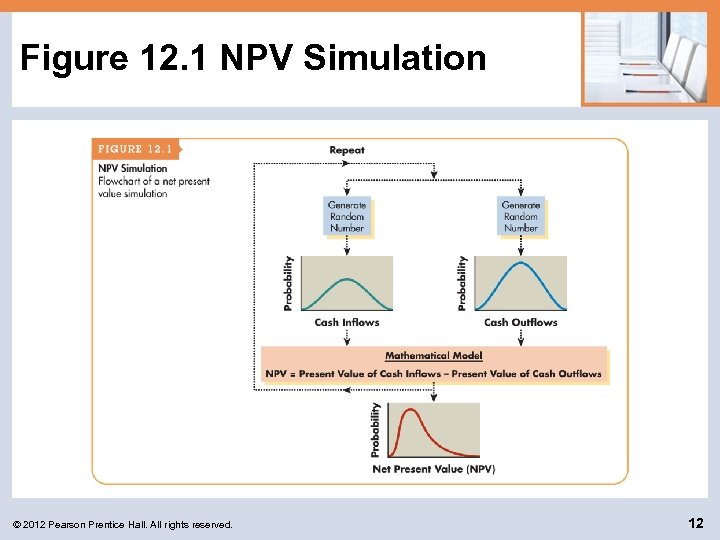
Figure 12. 1 NPV Simulation © 2012 Pearson Prentice Hall. All rights reserved. 12

Focus on Practice The Monte Carlo Method: The Forecast Is for Less Uncertainty – To combat uncertainty in the decision-making process, some companies use a Monte Carlo simulation program to model possible outcomes. – A Monte Carlo simulation program randomly generates values for uncertain variables over and over to simulate a model. – The simulation then requires project practitioners to develop low, high, and most likely cost estimates along with correlation coefficients. – One of the problems with using a Monte Carlo program is the difficulty of establishing the correct input ranges for the variables and determining the correlation coefficients for those variables. – A Monte Carlo simulation program requires the user to first build an Excel spreadsheet model that captures the input variables for the proposed project. What issues and what benefits can the user derive from this process? © 2012 Pearson Prentice Hall. All rights reserved. 13

International Risk Considerations • Exchange rate risk is the danger that an unexpected change in the exchange rate between the dollar and the currency in which a project’s cash flows are denominated will reduce the market value of that project’s cash flow. • In the short term, much of this risk can be hedged by using financial instruments such as foreign currency futures and options. • Long-term exchange rate risk can best be minimized by financing the project in whole or in part in the local currency. © 2012 Pearson Prentice Hall. All rights reserved. 14

Matter of Fact A 2001 survey of Chief Financial Officers (CFOs) found that more than 40% of the CFOs felt that it was important to adjust an investment project’s cash flows or discount rates to account foreign exchange risk. © 2012 Pearson Prentice Hall. All rights reserved. 15

International Risk Considerations (cont. ) • Political risk is much harder to protect against. Firms that make investments abroad may find that the host-country government can limit the firm’s ability to return profits back home. Governments can seize the firm’s assets, or otherwise interfere with a project’s operation. • The difficulties of managing political risk after the fact make it even more important that managers account for political risks before making an investment. • They can do so either by adjusting a project’s expected cash inflows to account for the probability of political interference or by using risk-adjusted discount rates in capital budgeting formulas. © 2012 Pearson Prentice Hall. All rights reserved. 16

International Risk Considerations (cont. ) Other special issues relevant for international capital budgeting include: – Taxes – Transfer pricing – Strategic, rather than financial, considerations © 2012 Pearson Prentice Hall. All rights reserved. 17

Risk-Adjusted Discount Rates Risk-adjusted discount rates (RADR) are rates of return that must be earned on a given project to compensate the firm’s owners adequately—that is, to maintain or improve the firm’s share price. © 2012 Pearson Prentice Hall. All rights reserved. 18

Personal Finance Example Talor Namtig is considering investing $1, 000 in either of two stocks—A or B. She plans to hold the stock for exactly 5 years and expects both stocks to pay $80 in annual end-ofyear cash dividends. At the end of the year 5 she estimates that stock A can be sold to net $1, 200 and stock B can be sold to net $1, 500. Her research indicates that she should earn an annual return on an average risk stock of 11%. Because stock B is considerably riskier, she will require a 14% return from it. Talor makes the following calculations to find the risk-adjusted net present values (NPVs) for the two stocks: © 2012 Pearson Prentice Hall. All rights reserved. 19

Personal Finance Example (cont. ) Although Talor’s calculations indicate that both stock investments are acceptable (NPVs > $0), on a risk-adjusted basis, she should invest in Stock B because it has a higher NPV. © 2012 Pearson Prentice Hall. All rights reserved. 20

Risk-Adjusted Discount Rates: Review of CAPM Using beta, bj, to measure the relevant risk of any asset j, the CAPM is rj = RF + [bj (rm – RF)] where rj RF bj rm = = required return on asset j risk-free rate of return beta coefficient for asset j return on the market portfolio of assets © 2012 Pearson Prentice Hall. All rights reserved. 21

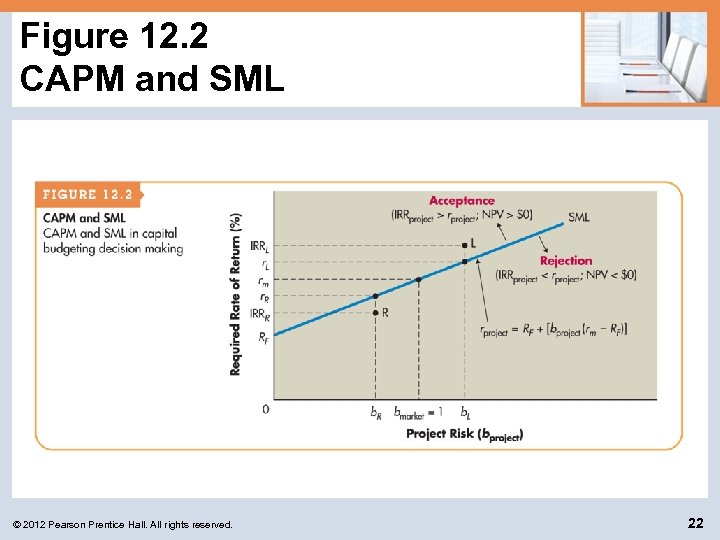
Figure 12. 2 CAPM and SML © 2012 Pearson Prentice Hall. All rights reserved.

Risk-Adjusted Discount Rates: Using CAPM to Find RADRs (cont. ) Figure 12. 2 shows two projects, L and R. • Project L has a beta, b. L, and generates an internal rate of return, IRRL. The required return for a project with risk b. L is r. L. – Because project L generates a return greater than that required (IRRL > r. L), project L is acceptable. – Project L will have a positive NPV when its cash inflows are discounted at its required return, r. L. • Project R, on the other hand, generates an IRR below that required for its risk, b. R (IRRR < r. R). – This project will have a negative NPV when its cash inflows are discounted at its required return, r. R. – Project R should be rejected. © 2012 Pearson Prentice Hall. All rights reserved. 23

Focus on Ethics and the Cost of Capital – On April 20, 2010 the Deepwater Horizon, an offshore drilling rig operated by Transocean Ltd. on behalf of BP, exploded and eventually sank in the Gulf of Mexico, killing 11 people. – To make matters worse, oil began spewing into the Gulf. – By June 2010, BP’s stock price was 50% below pre-crisis levels and the company’s bonds traded at levels comparable to junk rated companies. – Is the ultimate goal of the firm, to maximize the wealth of the owners for whom the firm is being operated, ethical? – Why might ethical companies benefit from a lower cost of capital than less ethical companies? © 2012 Pearson Prentice Hall. All rights reserved. 24

Risk-Adjusted Discount Rates: Applying RADRs Bennett Company wishes to apply the Risk-Adjusted Discount Rate (RADR) approach to determine whether to implement Project A or B. In addition to the data presented earlier, Bennett’s management assigned a “risk index” of 1. 6 to project A and 1. 0 to project B as indicated in the following table. The required rates of return associated with these indexes are then applied as the discount rates to the two projects to determine NPV. © 2012 Pearson Prentice Hall. All rights reserved. 25

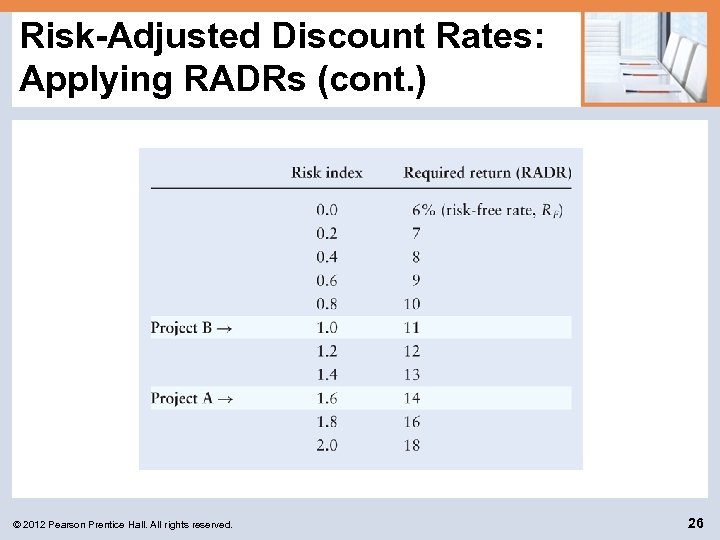
Risk-Adjusted Discount Rates: Applying RADRs (cont. ) © 2012 Pearson Prentice Hall. All rights

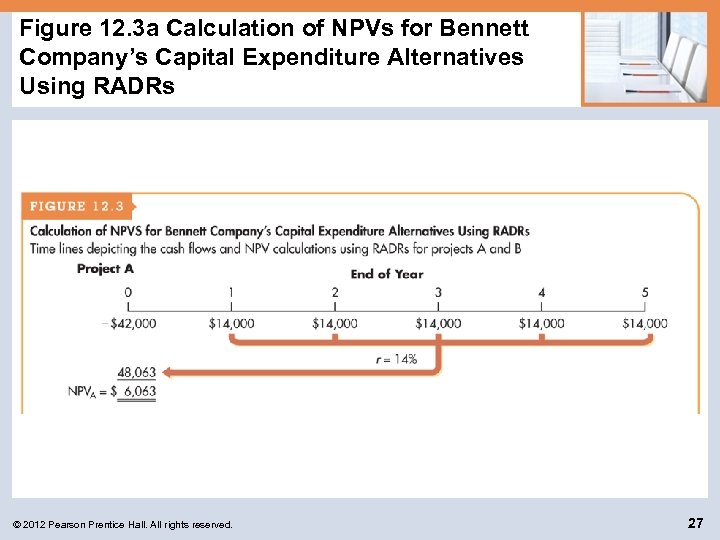
Figure 12. 3 a Calculation of NPVs for Bennett Company’s Capital Expenditure Alternatives Using

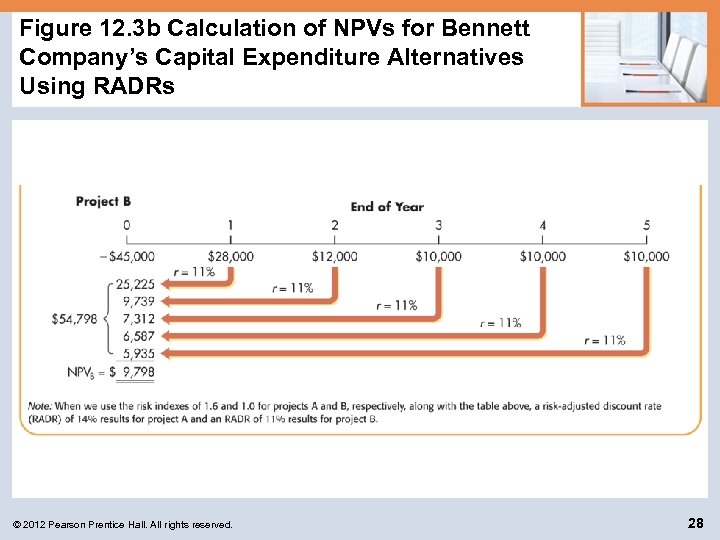
Figure 12. 3 b Calculation of NPVs for Bennett Company’s Capital Expenditure Alternatives Using

Risk-Adjusted Discount Rates: Applying RADRs (cont. ) Project A Project B © 2012 Pearson

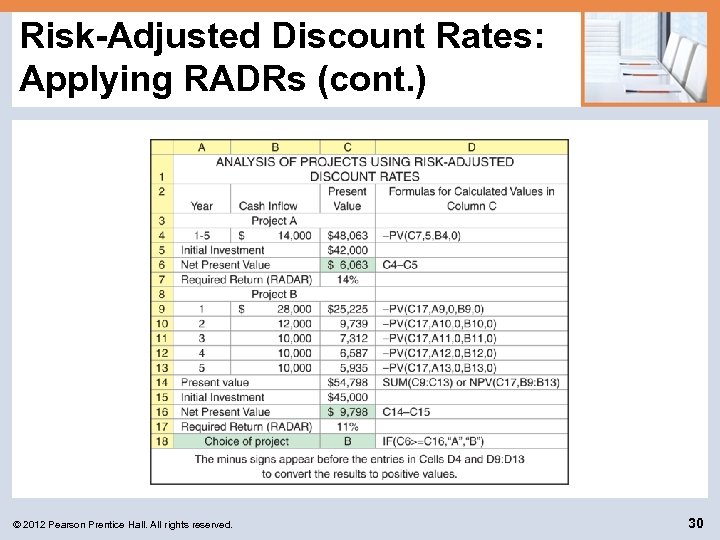
Risk-Adjusted Discount Rates: Portfolio Effects • As noted earlier, individual investors must hold diversified portfolios because they are not rewarded for assuming diversifiable risk. • Because business firms can be viewed as portfolios of assets, it would seem that it is also important that they too hold diversified portfolios. • Surprisingly, however, empirical evidence suggests that firm value is not affected by diversification. • In other words, diversification is not normally rewarded and therefore is generally not necessary. © 2012 Pearson Prentice Hall. All rights reserved. 31

Risk-Adjusted Discount Rates: Portfolio Effects (cont. ) • It turns out that firms are not rewarded for diversification because investors can do so themselves. • An investor can diversify more readily, easily, and costlessly simply by holding portfolios of stocks. © 2012 Pearson Prentice Hall. All rights reserved. 32

Table 12. 3 Bennett Company’s Risk Classes and RADRs © 2012 Pearson Prentice Hall.

Risk-Adjusted Discount Rates: RADRs in Practice (cont. ) Assume that the management of Bennett Company decided to use risk classes to analyze projects and so placed each project in one of four risk classes according to its perceived risk. The classes ranged from I for the lowest-risk projects to IV for the highest-risk projects. The financial manager of Bennett has assigned project A to class III and project B to class II. The cash flows for project A would be evaluated using a 14% RADR, and project B’s would be evaluated using a 10% RADR. The NPV of project A at 14% was calculated in Figure 12. 3 to be $6, 063, and the NPV for project B at a 10% RADR was shown in Table 12. 1 to be $10, 924. © 2012 Pearson Prentice Hall. All rights reserved. 34

Capital Budgeting Refinements: Comparing Projects With Unequal Lives • The financial manager must often select the best of a group of unequal-lived projects. • If the projects are independent, the length of the project lives is not critical. • But when unequal-lived projects are mutually exclusive, the impact of differing lives must be considered because the projects do not provide service over comparable time periods. © 2012 Pearson Prentice Hall. All rights reserved. 35

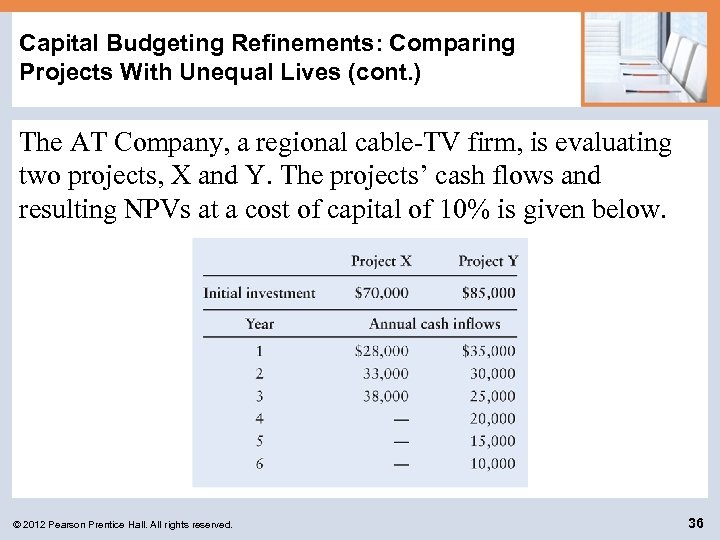
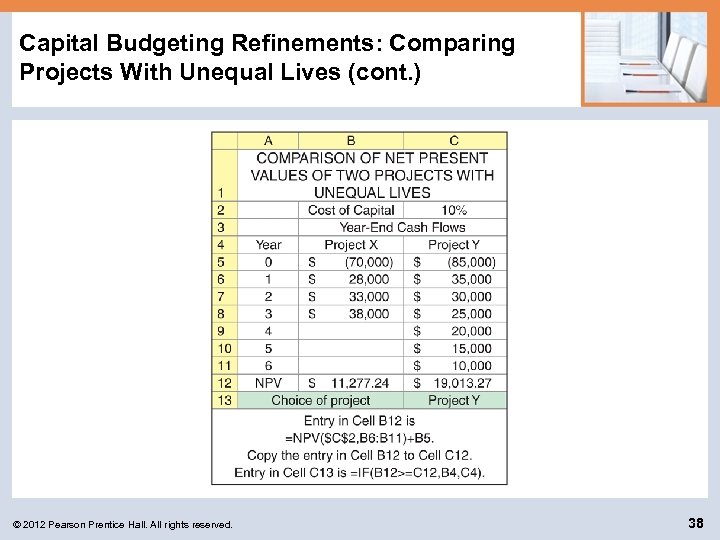
Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) The AT Company, a regional cable-TV firm, is evaluating two projects, X and Y. The projects’ cash flows and resulting NPVs at a cost of capital of 10% is given below. © 2012 Pearson Prentice Hall. All rights reserved. 36

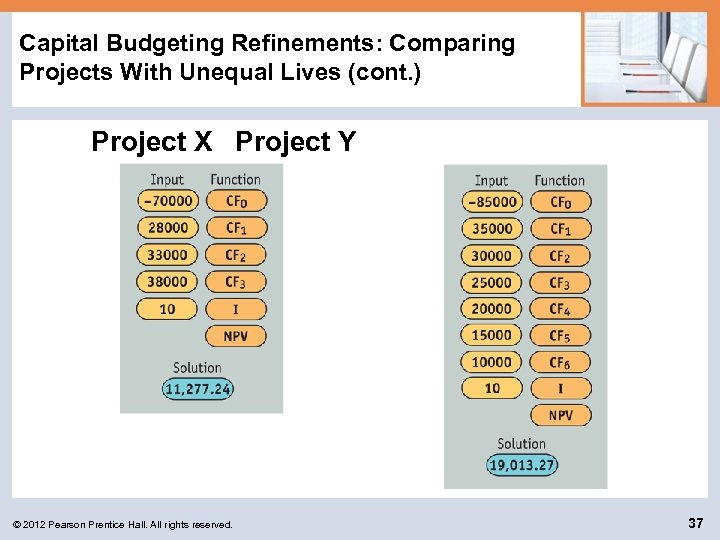
Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) Project X Project Y

Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) © 2012 Pearson Prentice

Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) Ignoring the difference in their useful lives, both projects are acceptable (have positive NPVs). Furthermore, if the projects were mutually exclusive, project Y would be preferred over project X. However, it is important to recognize that at the end of its 3 year life, project Y must be replaced, or renewed. © 2012 Pearson Prentice Hall. All rights reserved. 39

Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) The annualized net present value (ANPV) approach is an approach to evaluating unequal-lived projects that converts the net present value of unequal-lived, mutually exclusive projects into an equivalent annual amount (in NPV terms). Step 1 Calculate the net present value of each project j, NPVj, over its life, nj, using the appropriate cost of capital, r. Step 2 Convert the NPVj into an annuity having life nj. That is, find an annuity that has the same life and the same NPV as the project. Step 3 Select the project that has the highest ANPV. © 2012 Pearson Prentice Hall. All rights reserved. 40

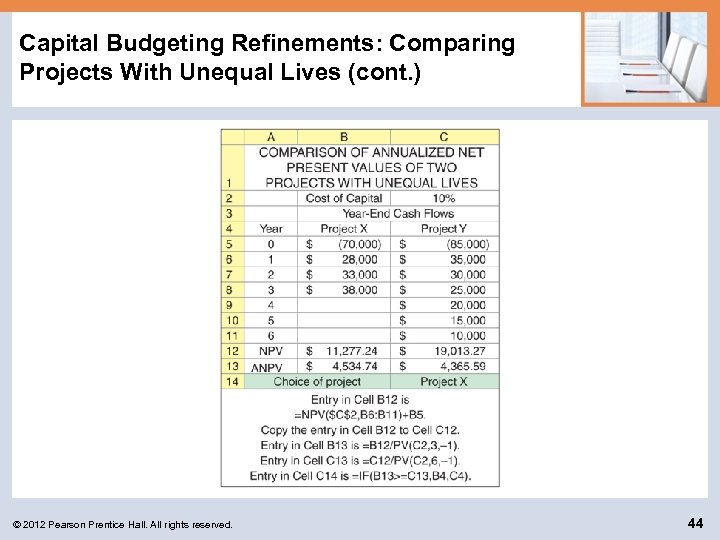
Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) By using the AT Company data presented earlier for projects X and Y, we can apply the three-step ANPV approach as follows: Step 1 The net present values of projects X and Y discounted at 10%—as calculated in the preceding example for a single purchase of each asset—are NPVX = $11, 277. 24 (table value = $11, 248) NPVY = $19, 013. 27 (table value = $18, 985) © 2012 Pearson Prentice Hall. All rights reserved. 41

Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) Step 2 In this step, we want to convert the NPVs from Step 1 into annuities. For project X, we are trying to find the answer to the question, what 3 year annuity (equal to the life of project X) has a present value of $11, 248 (the NPV of project X)? Likewise, for project Y we want to know what 6 -year annuity has a present value of $18, 985. Once we have these values, we can determine which project, X or Y, delivers a higher annual cash flow on a present value basis. © 2012 Pearson Prentice Hall. All rights reserved. 42

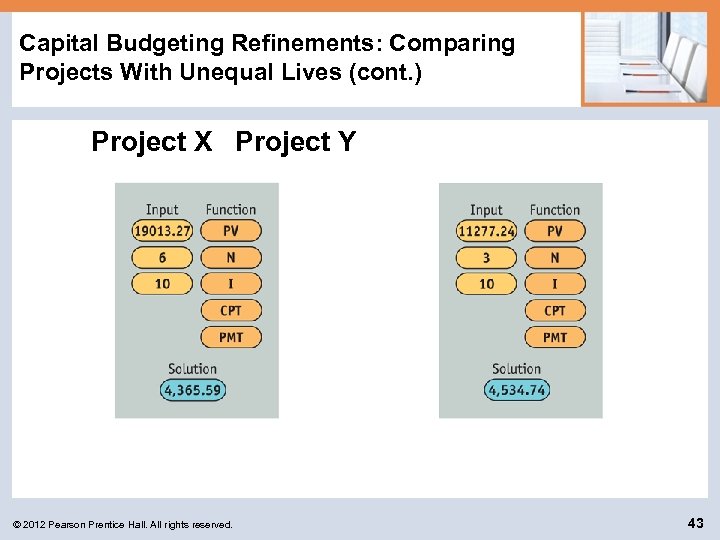
Capital Budgeting Refinements: Comparing Projects With Unequal Lives (cont. ) Step 3 Reviewing the ANPVs calculated in Step 2, we can see that project X would be preferred over project Y. Given that projects X and Y are mutually exclusive, project X would be the recommended project because it provides the higher annualized net present value. © 2012 Pearson Prentice Hall. All rights reserved. 45

Recognizing Real Options Real options are opportunities that are embedded in capital projects that enable managers to alter their cash flows and risk in a way that affects project acceptability (NPV). – Also called strategic options. By explicitly recognizing these options when making capital budgeting decisions, managers can make improved, more strategic decisions that consider in advance the economic impact of certain contingent actions on project cash flow and risk. NPVstrategic = NPVtraditional + Value of real options © 2012 Pearson Prentice Hall. All rights reserved. 46

Table 12. 4 Major Types of Real Options © 2012 Pearson Prentice Hall. All

Recognizing Real Options (cont. ) Assume that a strategic analysis of Bennett Company’s projects A and B finds no real options embedded in Project A but two real options embedded in B: 1. During it’s first two years, B would have downtime that results in unused production capacity that could be used to perform contract manufacturing; 2. Project B’s computerized control system could control two other machines, thereby reducing labor costs. © 2012 Pearson Prentice Hall. All rights reserved. 48

Recognizing Real Options (cont. ) Bennett’s management estimated the NPV of the contract manufacturing over the two years following implementation of project B to be $1, 500 and the NPV of the computer control sharing to be $2, 000. Management felt there was a 60% chance that the contract manufacturing option would be exercised and only a 30% chance that the computer control sharing option would be exercised. The combined value of these two real options would be the sum of their expected values. Value of real options for project B = (0. 60 $1, 500) + (0. 30 $2, 000) = $900 + $600 = $1, 500 © 2012 Pearson Prentice Hall. All rights reserved. 49

Recognizing Real Options (cont. ) Adding the $1, 500 real options value to the traditional NPV of $10, 924 for project B, we get the strategic NPV for project B. NPVstrategic = $10, 924 + $1, 500 = $12, 424 Bennett Company’s project B therefore has a strategic NPV of $12, 424, which is above its traditional NPV and now exceeds project A’s NPV of $11, 071. Clearly, recognition of project B’s real options improved its NPV (from $10, 924 to $12, 424) and causes it to be preferred over project A (NPV of $12, 424 for B > NPV of $11, 071 for A), which has no real options embedded in it. © 2012 Pearson Prentice Hall. All rights reserved. 50

Capital Rationing • Firm’s often operate under conditions of capital rationing —they have more acceptable independent projects than they can fund. • In theory, capital rationing should not exist—firms should accept all projects that have positive NPVs. • However, in practice, most firms operate under capital rationing. • Generally, firms attempt to isolate and select the best acceptable projects subject to a capital expenditure budget set by management. © 2012 Pearson Prentice Hall. All rights reserved. 51

Capital Rationing (cont. ) • The internal rate of return approach is an approach to capital rationing that involves graphing project IRRs in descending order against the total dollar investment to determine the group of acceptable projects. • The graph that plots project IRRs in descending order against the total dollar investment is called the investment opportunities schedule (IOS). • The problem with this technique is that it does not guarantee the maximum dollar return to the firm. © 2012 Pearson Prentice Hall. All rights reserved. 52

Capital Rationing (cont. ) Tate Company, a fast growing plastics company with a cost of capital of 10%, is confronted with six projects competing for its fixed budget of $250, 000. © 2012 Pearson Prentice Hall. All rights reserved. 53

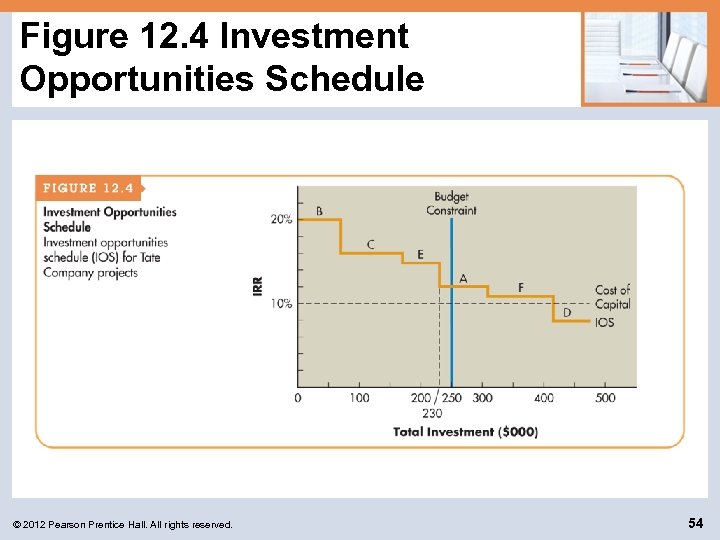
Figure 12. 4 Investment Opportunities Schedule © 2012 Pearson Prentice Hall. All rights reserved.

Capital Rationing (cont. ) • The net present value approach is an approach to capital rationing that is based on the use of present values to determine the group of projects that will maximize owners’ wealth. • It is implemented by ranking projects on the basis of IRRs and then evaluating the present value of the benefits from each potential project to determine the combination of projects with the highest overall present value. © 2012 Pearson Prentice Hall. All rights reserved. 55

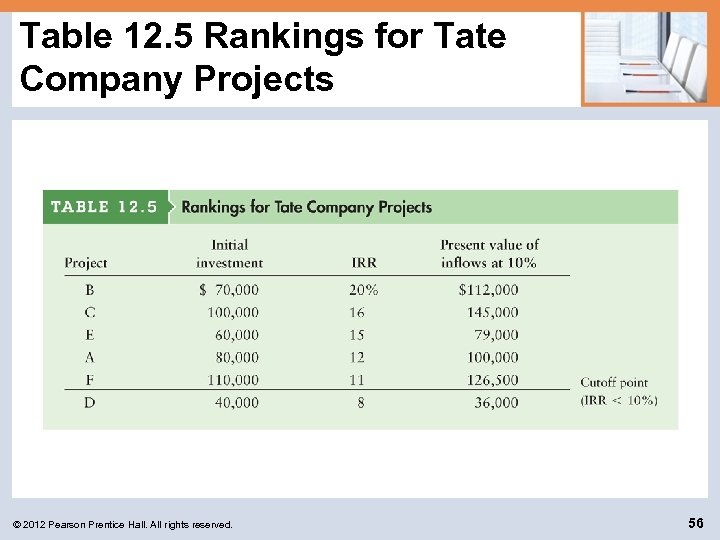
Table 12. 5 Rankings for Tate Company Projects © 2012 Pearson Prentice Hall. All

Review of Learning Goals LG 1 Understand the importance of recognizing risk in the analysis of capital budgeting projects. – The cash flows associated with capital budgeting projects typically have different levels of risk, and the acceptance of a project generally affects the firm’s overall risk. Thus it is important to incorporate risk considerations in capital budgeting. © 2012 Pearson Prentice Hall. All rights reserved. 57

Review of Learning Goals (cont. ) LG 2 Discuss risk and cash inflows, scenario analysis, and simulation as behavioral approaches for dealing with risk. – Risk in capital budgeting is the degree of variability of cash flows, which for conventional capital budgeting projects stems almost entirely from net cash flows. Finding the breakeven cash inflow and estimating the probability that it will be realized make up one behavioral approach for assessing capital budgeting risk. Scenario analysis is another behavioral approach for capturing the variability of cash inflows and NPVs. Simulation is a statistically based approach that results in a probability distribution of project returns. © 2012 Pearson Prentice Hall. All rights reserved. 58

Review of Learning Goals (cont. ) LG 3 Review the unique risks that multinational companies face. – Although the basic capital budgeting techniques are the same for multinational and purely domestic companies, firms that operate in several countries must also deal with exchange rate and political risks, tax law differences, transfer pricing, and strategic issues. © 2012 Pearson Prentice Hall. All rights reserved. 59

Review of Learning Goals (cont. ) LG 4 Describe the determination and use of risk-adjusted discount rates (RADRs), portfolio effects, and the practical aspects of RADRs. – The risk of a project whose initial investment is known with certainty is embodied in the present value of its cash inflows, using NPV. Two opportunities to adjust the present value of cash inflows for risk exist—adjust the cash inflows or adjust the discount rate. Because adjusting the cash inflows is highly subjective, adjusting discount rates is more popular. RADRs use a market-based adjustment of the discount rate to calculate NPV. © 2012 Pearson Prentice Hall. All rights reserved. 60

Review of Learning Goals (cont. ) LG 5 Select the best of a group of unequal-lived, mutually exclusive projects using annualized net present values (ANPVs). – The ANPV approach is the most efficient method of comparing ongoing, mutually exclusive projects that have unequal usable lives. It converts the NPV of each unequallived project into an equivalent annual amount—its ANPV. © 2012 Pearson Prentice Hall. All rights reserved. 61

Review of Learning Goals (cont. ) LG 6 Explain the role of real options and the objective and procedures for selecting projects under capital rationing. – Real options are opportunities that are embedded in capital projects and that allow managers to alter their cash flow and risk in a way that affects project acceptability (NPV). By explicitly recognizing real options, the financial manager can find a project’s strategic NPV. – Capital rationing exists when firms have more acceptable independent projects than they can fund. The two basic approaches for choosing projects under capital rationing are the internal rate of return approach and the net present value approach. The NPV approach better achieves the objective of using the budget to generate the highest present value of inflows. © 2012 Pearson Prentice Hall. All rights reserved. 62

Chapter Resources on My. Finance. Lab • Chapter Cases • Group Exercises • Critical

Integrative Case: Lasting Impressions Company Lasting Impressions (LI) Company’s general manager has proposed the purchase of one of two large, six-color presses designed for long, high-quality runs. The purchase of a new press would enable LI to reduce its cost of labor and therefore the price to the client, putting the firm in a more competitive position. The key financial characteristics of the old press and of the two proposed presses are summarized in what follows. © 2012 Pearson Prentice Hall. All rights reserved. 64

Integrative Case: Lasting Impressions Company (cont. ) Press A This highly automated press can be purchased for $830, 000 and will require $40, 000 in installation costs. It will be depreciated under MACRS using a 5 -year recovery period. At the end of the 5 years, the machine could be sold to net $400, 000 before taxes. If this machine is acquired, it is anticipated that the following current account changes would result: – Cash: +$25, 400 – Accounts receivable: +$120, 000 – Inventories: – $20, 000 – Accounts payable: +$35, 000 © 2012 Pearson Prentice Hall. All rights reserved. 65

Integrative Case: Lasting Impressions Company (cont. ) Press B This press is not as sophisticated as press A. It costs $640, 000 and requires $20, 000 in installation costs. It will be depreciated under MACRS using a 5 -year recovery period. At the end of 5 years, it can be sold to net $330, 000 before taxes. Acquisition of this press will have no effect on the firm’s net working capital investment. © 2012 Pearson Prentice Hall. All rights reserved. 66

Integrative Case: Lasting Impressions Company (cont. ) The firm estimates that its earnings before depreciation, interest, and taxes with the old press and with press A or press B for each of the 5 years would be as shown in Table 1. The firm is subject to a 40% tax rate. The firm’s cost of capital, r, applicable to the proposed replacement is 14%. © 2012 Pearson Prentice Hall. All rights reserved. 67

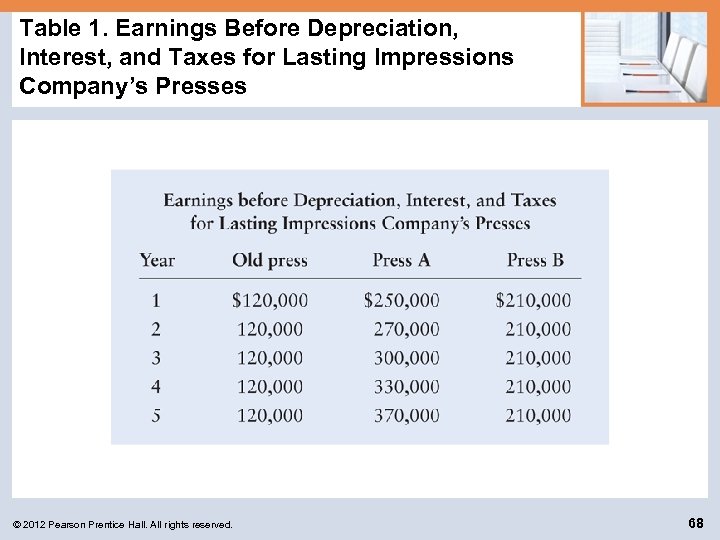
Table 1. Earnings Before Depreciation, Interest, and Taxes for Lasting Impressions Company’s Presses ©

Integrative Case: Lasting Impressions Company (cont. ) a. For each of the two proposed replacement presses, determine: 1. Initial investment. 2. Operating cash inflows. (Note: Be sure to consider the depreciation in year 6. ) 3. Terminal cash flow. (Note: This is at the end of year 5. ) b. Using the data developed in part a, find and depict on a time line the relevant cash flow stream associated with each of the two proposed replacement presses, assuming that each is terminated at the end of 5 years. © 2012 Pearson Prentice Hall. All rights reserved. 69

Integrative Case: Lasting Impressions Company (cont. ) c. Using the data developed in part b, apply each of the following decision techniques: 1. Payback period. (Note: For year 5, use only the operating cash inflows—that is, exclude terminal cash flow—when making this calculation. ) 2. Net present value (NPV). 3. Internal rate of return (IRR). d. Draw net present value profiles for the two replacement presses on the same set of axes, and discuss conflicting rankings of the two presses, if any, resulting from use of NPV and IRR decision techniques. © 2012 Pearson Prentice Hall. All rights reserved. 70

Integrative Case: Lasting Impressions Company (cont. ) e. Recommend which, if either, of the presses the firm should acquire if the firm has (1) unlimited funds or (2) capital rationing. f. What is the impact on your recommendation of the fact that the operating cash inflows associated with press A are characterized as very risky in contrast to the low-risk operating cash inflows of press B? © 2012 Pearson Prentice Hall. All rights reserved. 71