CHAPTER 12 Inventory Management 1 Agenda Inventory

CHAPTER 12 Inventory Management 1

Agenda Inventory Management? Inventory Reasons for holding/avoiding inventory Objective of inventory management Continuous (perpetual) inventory counting system Constant demand lead time : EOQ Model Uncertain demand constant lead time Economic Production Model (EPQ) Single-Period Model (newsboy Problem) 2

What is Inventory Management? 3

Inventory: A stock or store of goods. Inventory is created when receiving rate exceeds usage rate incoming raw material exceeds production consumption production exceeds demand Inventory can be measured in physical units money 4

Inventory Examples Manufacturing firms carry supplies of raw materials, purchased parts, finished items, spare parts, tools, . . Department stores carry clothing, furniture, stationery, appliances, . . . Hospitals stock drugs, surgical supplies, life-monitoring equipment, sheets, pillow cases, . . . Supermarkets stock fresh and canned foods, packaged and frozen foods, household supplies, . . . 5

Why might we want to build inventories? a. Customer service: For customers that have immediate or seasonal demands, finished goods inventory can speed up delivery and reduce stockouts and backorders. b. Ordering costs: Costs associated with purchasing, follow-up, receiving, and paperwork are incurred each time an order is placed. By ordering in larger quantities, the resulting inventory provides a means of obtaining and handling materials in economic lot sizes. c. Setup costs: Production orders have similar costs associated with each setup, and machines may be unproductive for several hours each time the product is switched. > Labor and time to make changeover > May include scrap and rework 6

Why might we want to build inventories? (cont’d) c. Stabilizing output rates: Inventories can be used to cover peaks in demand, level production activities, stabilize employment, and improve labor relations. d. Transportation costs: Transportation costs can be reduced by building inventories and shipping full truckloads. e. Quantity discounts. Ordering large quantities can provide a hedge against future price increases and provide a means to obtain quantity discounts. 7

Why might we want to avoid inventories? a. Collectively called “inventory holding cost. ” The cost to keep an item on hand for a year typically ranges from 25 percent to 40 percent of the item’s value. b. Cost components • Interest or opportunity cost of capital — time value of money • Storage and handling—warehouse facilities and labor • Taxes and insurance—usually proportional to inventory value • Shrinkage - Pilferage - Obsolescence - Deterioration 8

Objective of Inventory Management To achieve satisfactory levels of customer service while keeping inventory costs within reasonable bounds Right goods, right place, right time, right quantity Goal: matching supply with demand! 9

Basic Inventory Management Questions How much to order When to order? Purchase Order Description Qty. Microwave 1000 10

Effective Inventory Systems? 11

Effective Inventory Management 1. A reliable forecast of demand 2. Knowledge of lead times and lead time variability 3. Reasonable estimates of • Holding costs • Ordering costs • Shortage costs 4. A classification system 5. An inventory Counting system • Types 12

1. Demand Forecast & 2. Lead Time Need reliable estimates of the amount and timing of demand Lead Time: Time interval between placing and receiving the order - Lead time variability: the greater the potential variability, the greater the need for additional stock to reduce the risk of a shortage between deliveries 13

3. Inventory Costs cont. b. Holding (carrying) cost: Physically holding item in storage. - Holding costs are stated in either way: a percentage of unit price 2. a dollar amount per unit 1. c. Shortage costs: Costs resulting when demand exceeds supply. - It is often difficult to quantify shortage costs. One objective of Inventory Control is to minimize the sum of these costs by balancing them. 14

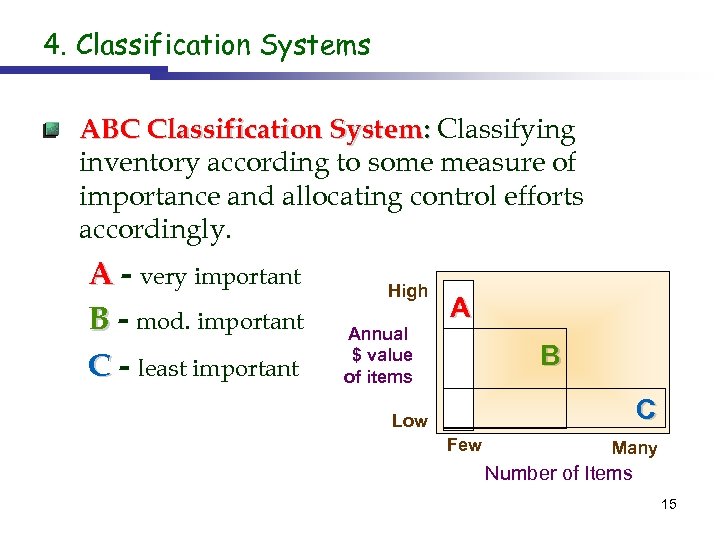4. Classification Systems ABC Classification System: Classifying inventory according to some measure of importance and allocating control efforts accordingly. A - very important B - mod. important C - least important High Annual $ value of items A B C Low Few Many Number of Items 15

Uses of ABC Approach Class A typically contains about 10 -20% of the items and 60 -70% of the annual dollar value Receive close attention: frequent reviews make sure customer service levels Class C contains about 50 -60% of the items, but only 10 -15% of the dollar value Receive only loose control, usually order in large quantities Class B is between the two extremes 16

5. Inventory Counting Systems - Types Periodic system: Physical count of items made at periodic intervals (weekly, monthly) - Good: Economics of scale - Bad: Lack of control between reviews, carry extra stock to protect against shortages between reviews Continuous (perpetual) system: System that keeps track of removals from inventory continuously, thus monitoring current levels of each item. Fixed quantity is ordered when a certain level is reached - Good: keep constant count of inventory, fixed order quantity - Bad: higher record keeping cost, periodic inventory counting is still required Two-bin system: Two containers of inventory; reorder when the first is empty - Good: simple, cheap, need not record each withdrawal - Bad: reorder card may not be turned in for some reasons 17

Self Test 1. The objective of inventory management is to minimize the cost of holding inventory. F 2. The overall objective of inventory management is to achieve satisfactory levels of customer service while keeping inventory costs reasonable. T 3. In the A-B-C approach, C items typically represent about 15 percent of the number of items, but 60 percent of the dollar usage. F 4. The two basic issues in inventory are how much to order and when to order. T 18

Continuous (perpetual) System with Constant Demand Lead Time – EOQ (basic) 19

Basic Economic Order Quantity Model (EOQ) Assumptions: 1. Ordering in batch from supplier. 2. Only one product is involved. 3. Constant demand rate. Demand is spread evenly throughout the year. 4. Constant lead time. Lead time does not vary much for a long enough time. 5. Single delivery for each order. 6. A single flat unit price from the supplier. Standard goods 20

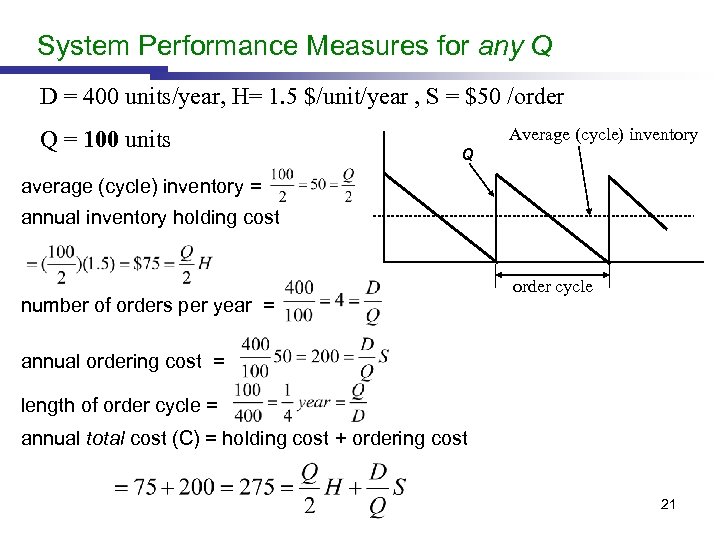System Performance Measures for any Q D = 400 units/year, H= 1. 5 $/unit/year , S = $50 /order Q = 100 units Average (cycle) inventory Q average (cycle) inventory = annual inventory holding cost number of orders per year = order cycle annual ordering cost = length of order cycle = annual total cost (C) = holding cost + ordering cost 21

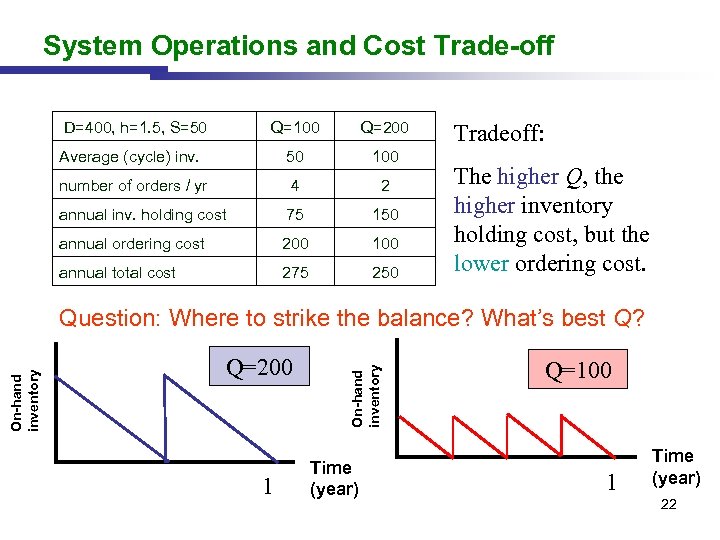System Operations and Cost Trade-off D=400, h=1. 5, S=50 Q=100 Q=200 Average (cycle) inv. 50 100 number of orders / yr 4 2 annual inv. holding cost 75 150 annual ordering cost 200 100 annual total cost 275 250 Tradeoff: The higher Q, the higher inventory holding cost, but the lower ordering cost. Q=200 1 On-hand inventory Question: Where to strike the balance? What’s best Q? Time (year) Q=100 1 Time (year) 22

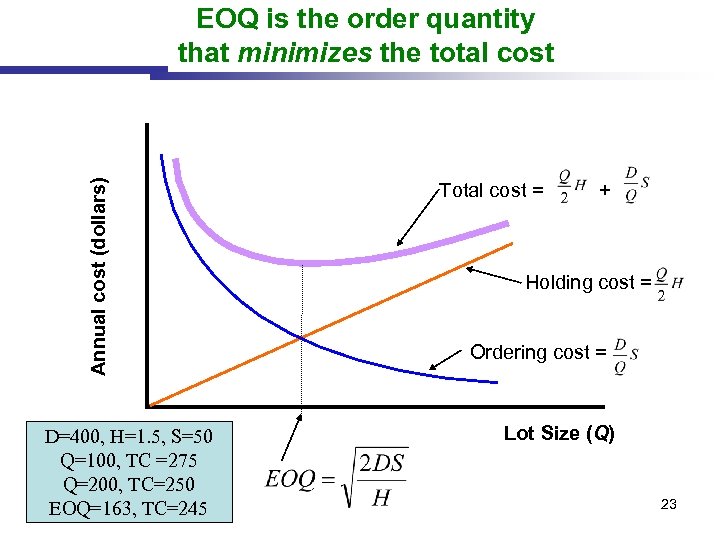Annual cost (dollars) EOQ is the order quantity that minimizes the total cost D=400, H=1. 5, S=50 Q=100, TC =275 Q=200, TC=250 EOQ=163, TC=245 Total cost = + Holding cost = Ordering cost = Lot Size (Q) 23

EOQ Model How much to order? Answer: EOQ = where D = annual demand, H = annual unit holding cost When to order? Instantaneous replenishment, i. e. lead time =0 Answer: when the inventory = 0 Constant replenishment lead time = L Answer ? 24

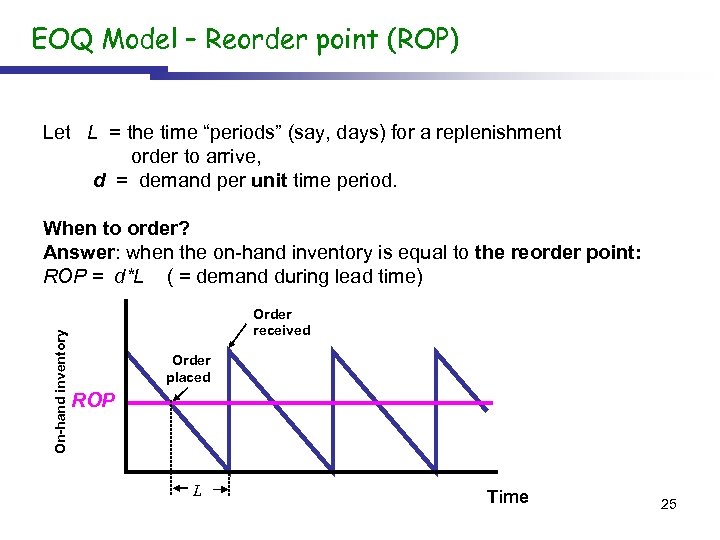EOQ Model – Reorder point (ROP) Let L = the time “periods” (say, days) for a replenishment order to arrive, d = demand per unit time period. On-hand inventory When to order? Answer: when the on-hand inventory is equal to the reorder point: ROP = d*L ( = demand during lead time) Order received Order placed ROP L Time 25

Example 1 Demand for a certain radial tires at a tire company is 800 units per month. Each tire costs the company $80. Ordering costs are $75, and the annual carrying costs are 20 percent of the purchase price. Lead time is 5 days and assume the company operates 288 days a year. D = 800 * 12 = 9600 /yr Match! S = $75 /order P = $80, r = 0. 20 H = r. P = $80 * 0. 2 = $16 /unit · yr 26

Solution to Example 1 1. How many tires should the manager order in each lot? 2. What is the company's average inventory of this tire? 3. How often will an order be placed (length of order cycle)? 27

Solution to Example 1 (Cont. ) 4. How many times per year will an order be placed? 5. How much does the company spend annually on ordering costs? 6. How much does the company spend annually on holding (carrying) costs? 28

Solution to Example 1 (Cont. ) 7. What is the total annual cost if the EOQ quantity is ordered? OR The ordering and carrying costs are equal at the EOQ 29

Solution to Example 1 (Cont. ) 8. What is the reorder point (ROP)? 30

Continuous (perpetual) System with Uncertain Demand Constant Lead Time 31

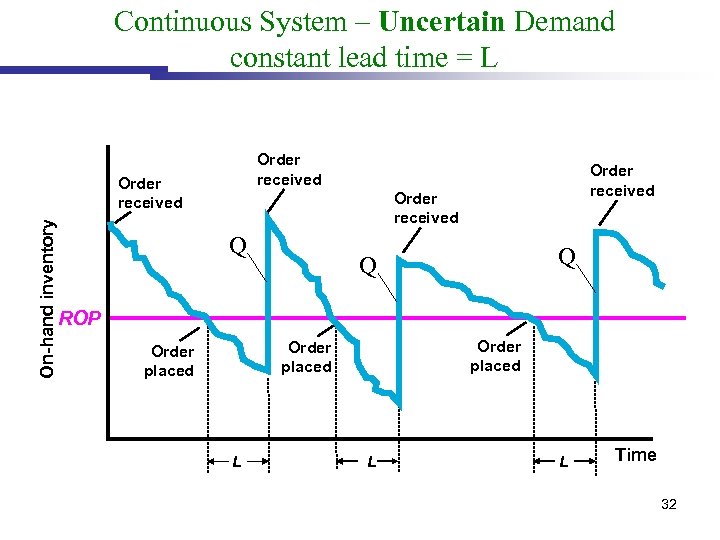Continuous System – Uncertain Demand constant lead time = L Order received On-hand inventory Order received Q Q Q ROP Order placed L L L Time 32

Continuous System – Uncertain Demand constant lead time = L How much to order? Answer: EOQ = where E[D] = average (expected) annual demand, H = annual unit holding cost When to order? Reorder Point (ROP)? 33

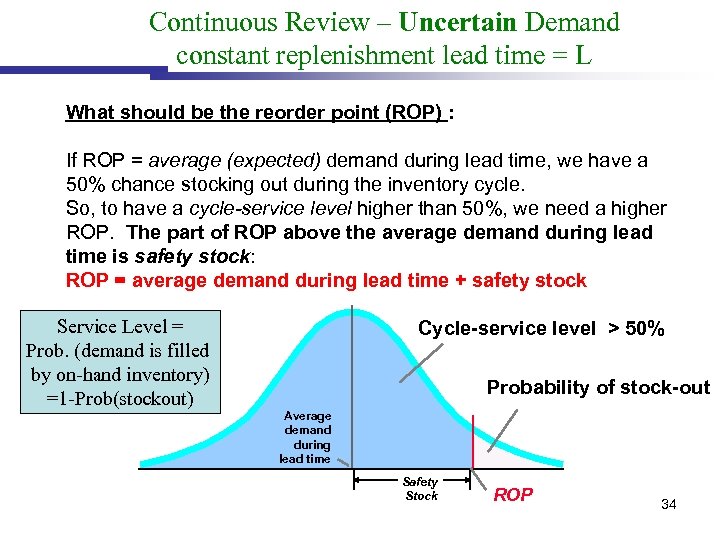Continuous Review – Uncertain Demand constant replenishment lead time = L What should be the reorder point (ROP) : If ROP = average (expected) demand during lead time, we have a 50% chance stocking out during the inventory cycle. So, to have a cycle-service level higher than 50%, we need a higher ROP. The part of ROP above the average demand during lead time is safety stock: ROP = average demand during lead time + safety stock Service Level = Prob. (demand is filled by on-hand inventory) =1 -Prob(stockout) Cycle-service level > 50% Probability of stock-out Average demand during lead time Safety Stock ROP 34

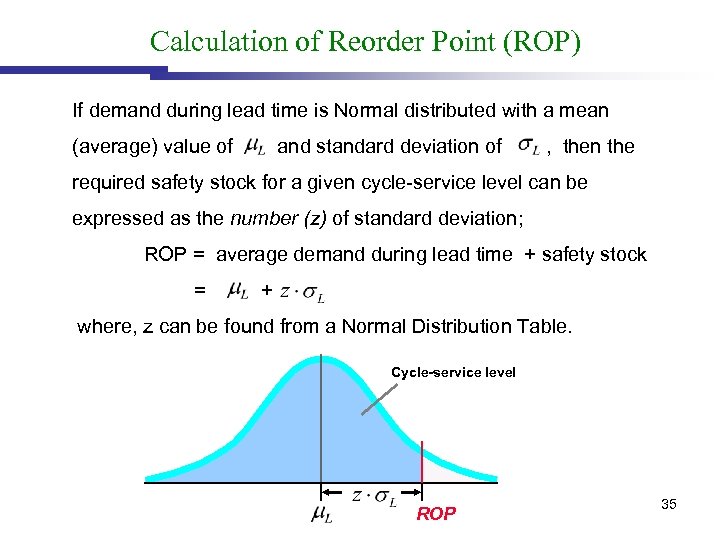Calculation of Reorder Point (ROP) If demand during lead time is Normal distributed with a mean (average) value of and standard deviation of , then the required safety stock for a given cycle-service level can be expressed as the number (z) of standard deviation; ROP = average demand during lead time + safety stock = + where, z can be found from a Normal Distribution Table. Cycle-service level ROP 35

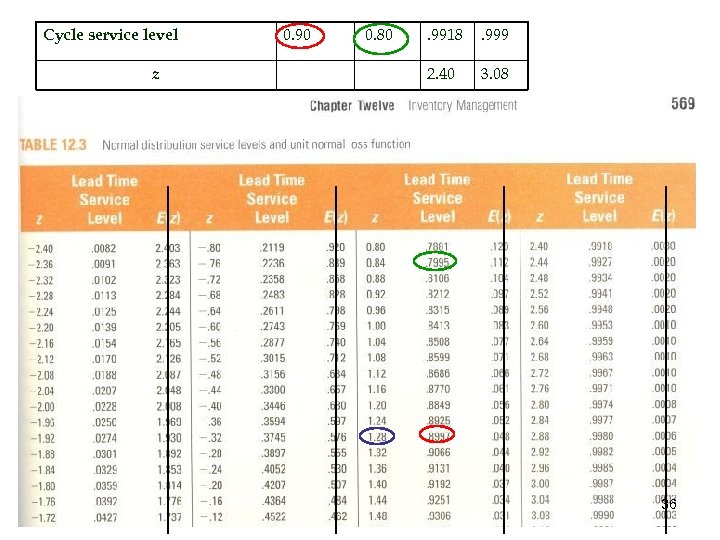Cycle service level z 0. 90 0. 80 . 9918 . 999 1. 28 0. 84 2. 40 3. 08 36

Calculation of Often demand distribution data is not expressed in terms of replenishment lead time. Suppose we know that the demand per “time period” (say, week) is Normal distributed with a mean value of and a standard deviations of. The inventory replenishment lead time is L time periods. Then, the demand during lead time will be Normal distributed with a mean value of and standard deviation of 37

Example 2 The Discount Appliance Store uses a continuous review system. One of the company’s items has the following characteristics: Demand = 10 units/wk (assume 52 weeks per year) Ordering/setup cost (S) = $45/order Holding cost (H) = $12/unit/year Lead time (L) = 3 weeks Standard deviation in weekly demand = 8 units Cycle-service level = 70% a. What is the optimal order quantity for this item? b. What is the desired safety stock? c. What is the desired reorder point R? 38

Example 2 (solution) a. The optimal order quantity is the EOQ: D = (10/wk)*(52 wk/yr) = 520 /yr; b. Safety stock: For a cycle-service level of 70%, z = 0. 52 (from Normal Table) safety stock (ss) = c. Reorder point (R): average demand during lead time: R = average demand during lead time + safety stock = + z = 30 + 7 = 37 39

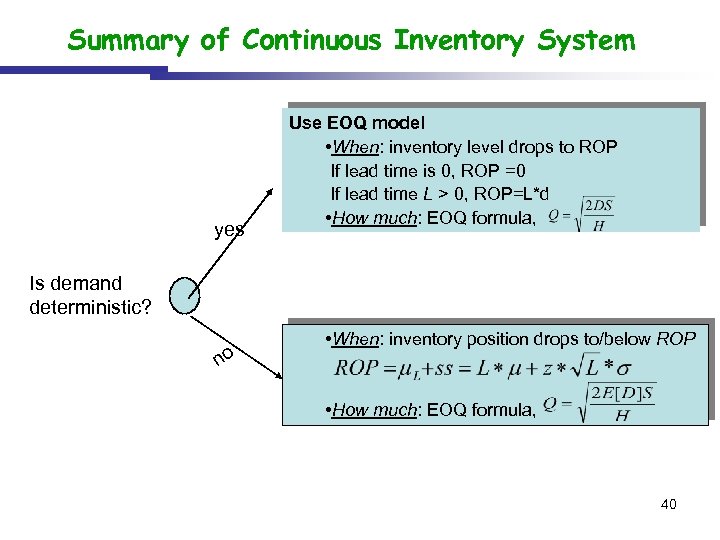Summary of Continuous Inventory System yes Use EOQ model • When: inventory level drops to ROP If lead time is 0, ROP =0 If lead time L > 0, ROP=L*d • How much: EOQ formula, Is demand deterministic? no • When: inventory position drops to/below ROP • How much: EOQ formula, 40

Economic Production Quantity (EPQ) 41

Basic Economic Production Quantity Model (EPQ) Assumptions: 1. Produces in batch and production rate is constant. 2. Only one product is involved. 3. Constant demand rate. Demand is spread evenly throughout the year. 4. Constant lead time. Lead time does not vary much for a long enough time. 5. Usage occurs continually, but production occurs periodically. 6. Capacity to produce a part exceeds the part's usage rate. Standard goods 42

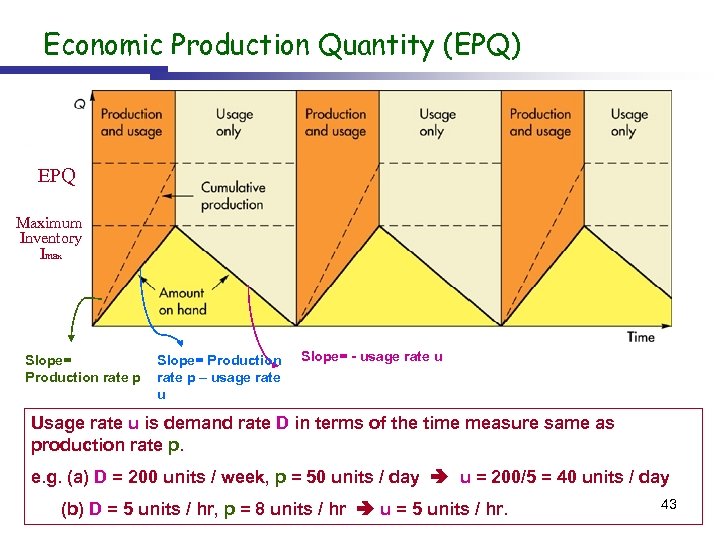Economic Production Quantity (EPQ) EPQ Maximum Inventory Imax Slope= Production rate p – usage rate u Slope= - usage rate u Usage rate u is demand rate D in terms of the time measure same as production rate p. e. g. (a) D = 200 units / week, p = 50 units / day u = 200/5 = 40 units / day (b) D = 5 units / hr, p = 8 units / hr u = 5 units / hr. 43

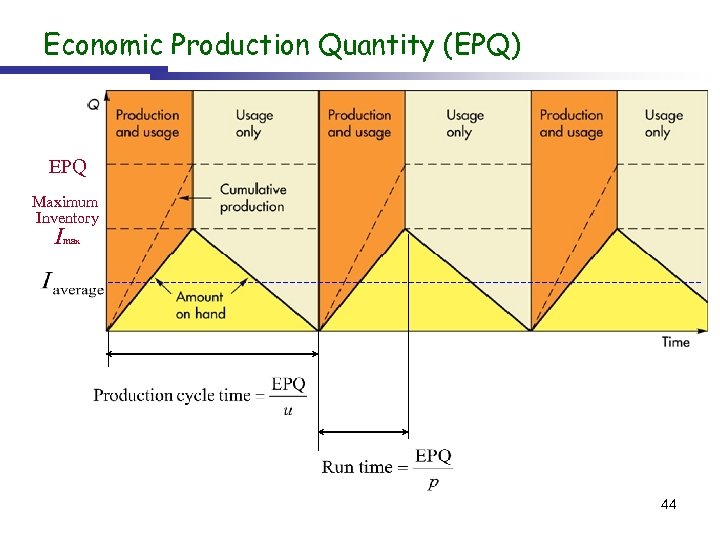Economic Production Quantity (EPQ) EPQ Maximum Inventory Imax 44

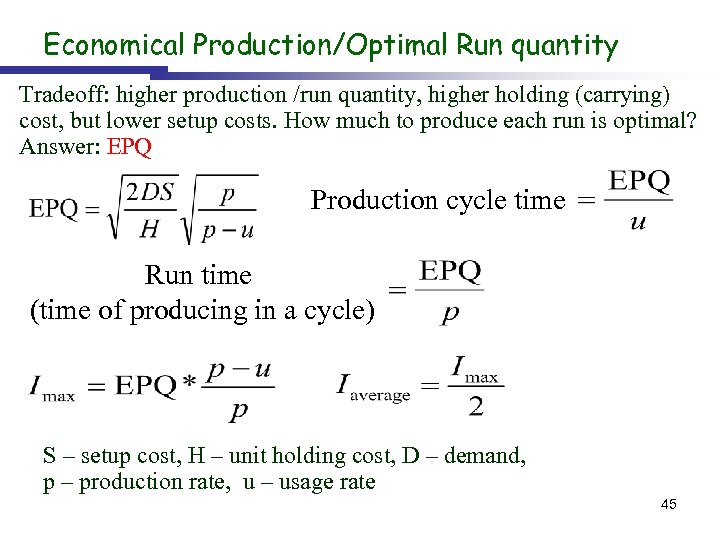Economical Production/Optimal Run quantity Tradeoff: higher production /run quantity, higher holding (carrying) cost, but lower setup costs. How much to produce each run is optimal? Answer: EPQ Production cycle time Run time (time of producing in a cycle) S – setup cost, H – unit holding cost, D – demand, p – production rate, u – usage rate 45

Example 3 A toy manufacturer uses 48, 000 rubber wheels per year for its popular dump truck series. The firm makes its own wheels, which it can produce at a rate 800 per day. The toy trucks are assembled uniformly over entire year. Carrying cost is $1 per wheel a year. Setup costs for a production run of wheels is $45. The firm operates 240 days per year. 46

Solution to Example 3 1. What is the optimal size of a production run? 2. What is the length of each production run? 3. What is cycle time for the optimal run size? 47

Solution to Example 3 (Cont. ) 4. What is the maximum inventory level? the average inventory level? 5. What is the average annual cost for holding inventory? for setting up production? TC = $1800 48

Single-Period Model -- Newsboy Problem 49

Single-Period Model Assumptions: 1. Only one product is involved. 2. Uncertain bulk demand realizes in a selling season. We have a demand distribution estimated from past pattern and belief of future trend. 3. A single order arrives before selling season. 4. Excess inventory is salvaged after selling season. Fashion goods 50

Newsboy Problem – An Example: A newsboy can buy copies of a newspaper for 25 cents early in the morning each day and sell them for 85 cents during the day. He is paid 5 cents for unsold copies. Underage cost (shortage cost): the marginal cost of under-stocking one unit. Cunderage = 0. 85 -0. 25 = $0. 60 per copy Overage cost (excess cost): the marginal cost of over-stocking one unit. Coverage = 0. 25 -0. 05 = $0. 20 per copy 51

Newsboy Solution The goal: Identify the order quantity that minimizes the sum of underage and overage costs Newsboy solution – optimal stocking quantity Te cost minimum order quantity guarantees a service level (percentage of chance that demand is satisfied) This percentage is called “Newsboy critical fractile” 52

Newsboy Problem – An Example: The newsboy has an underage cost of $ 0. 60/unit, and an overage cost of $0. 20/unit. The demand is approximately normal with a mean of 1000 copies per day (µ=1000) and standard deviation of 10 copies per day (σ=10). Service Level = Prob. (demand is filled by on-hand inventory) =1 -Prob(stockout) 53