e61118f79a705065851c44f8a565bb15.ppt
- Количество слайдов: 51

Chapter 12: Differential Games, Distributed System, and Impulse Control More than one decision maker, each having separate objective functions which each is trying to maximize, subject to a set of differential equations. The theory of differential games, Distributed parameter systems, Impulse control, Allow to make discrete changes in the state variables at selected instants of time in an optimal fashion.

12. 1 Differential Games Different types of solutions such as minimax, Nash, Pareto-optimal, along with possibilities of cooperation and bargaining. 12. 1. 1 Two Person Zero-Sum Differential Games which player 1 wants to maximize and player 2 wants to minimize.

is the minimax solution. The necessary conditions for u* and v* , is a saddle point of the Hamiltonian function H. when U=V=E 1,

12. 1. 2 Nonzero-Sum Differential Games N players, represent the control variable for the ith player, denote the objective function which the ith player wants to maximize. A Nash solution:

Open-Loop Nash Solution for all Closed-Loop Nash Solution we must recognize the dependence of the other player’s actions on the state variable x. Therefore,

Interpretation to the adjoint variable i. Any perturbation x in the state vector causes them to revise their controls by the amount 12. 1. 3 An Application to the Common-Property Fishery Resource Let denote the turnpike (or optimal biomass) level given by (10. 12).

As shown in Exercise 10. 2, We also assume that which means that producer 1 is more efficient than producer 2, i. e. , producer 1 can make a positive profit at any level in the interval , while producer 2 loses money in the same interval, except at where he breaks even. For both producers make positive profits.

As far as producer 1 is concerned, he wants to attain his turnpike level , if If and if then from (12. 26) producer 2 will fish at his maximum rate until the fish stock is driven to At this level it is optimal for producer 1 to fish at a rate which maintains the fish stock at level in order to keep producer 2 from fishing.

The Nash solution; The direct verification involves defining a modified growth function: And using the Green’s theorem results of Section 10. 1. 2. Since by assumption, we have

for From (10. 12) with g replaced by g 1, it can be shown that the new turnpike level for producer 1 is which defines the optimal policy (12. 27)(12. 28) for producer 1. The optimality of (12. 26) for producer 2 follows easily. Suppose that producer 1 originally has sole possession of the fishery, but anticipates a rival entry. Producer 1 will switch from his own optimal sustained yield to a more intensive exploitation policy prior to the anticipated entry. A Nash competitive solution involving N 2 producers results in the long-run dissipation of economic rents.

Model for licensing of fishermen let the control variable vi denote the capital stock of the ith producer and let the concave function f(vi), with f(0)=0, denote the fishing mortality function, for i=1, 2, …, N. This requires the replacement of in the previous model by f(vi). Application of differential games to fishery management, , Haurie, and Kaitala (1984, 1985) and , Ruusunen, and Kaitala (1986, 1990). Applications to problems in environmental management, Carraro and Filar (1995). Applications of marketing in general and optimal advertising, Bensoussan, Bultez, and Naert(1978),

Deal, Sethi, and Thompson(1979), Deal(1979), J rgensen(1982 a), Rao(1984, 1990), Dockner and J rgensen(1986, 1992), Chintagunta and Vilcassim(1992), Chingtagunta and Jain(1994, 1995), and Fruchter(1999). A survey of the literature is done by J rgensen(1982 a) and a monograph is written by Erickson(1991). For applications of differential games to economics and management science in general, see the book by Dockner, J rgensen , Long, Sorger(2000).

12. 2 Distributed Parameter Systems in which the state and control variables are defined in terms of space as well as time dimensions are called distributed parameter systems and are described by a set of partial differential or difference equations. In the analogous distributed parameter advertising model we must obtain the optimal advertising expenditure at every geographic location of interest at each instant of time, see Seidman, Sethi, and Derzko(1987). In section 12. 2. 2 we will discuss a cattle-ranching model of Derzko, Sethi and Thompson(1980), in which the spatial dimension measures the age of a cow.

Let y denote a one dimensional spatial vector, let t denote time, and let x(t, y) be a one dimensional state variable, Let u(t, y) denote a control variable, and let the state equation be For t [0, T ] and y [0, h ]. We denote the region [0, T ]x [0, h] by D, and we let its boundary D be split into two parts and as shown in Figure 12. 1. The initial conditions will be stated on the part of the boundary D as

x 0(y) gives the starting distribution of x with respect to the spatial coordinate y. The function v(t) in (12. 33) is an exogenous breeding function at time t of x when y=0. In the cattle ranching example in Section 12. 2. 2, v(t) measures the number of newly born calves at time t. Let F(t, y, x, u) denote the profit rate when x(t, y)=x, u(t, y)=u at a point (t, y) in D. Let Q(t) be the value of one unit of x(t, h) at time t and let S(y) be the value of one unit of x(T, y) at time T.
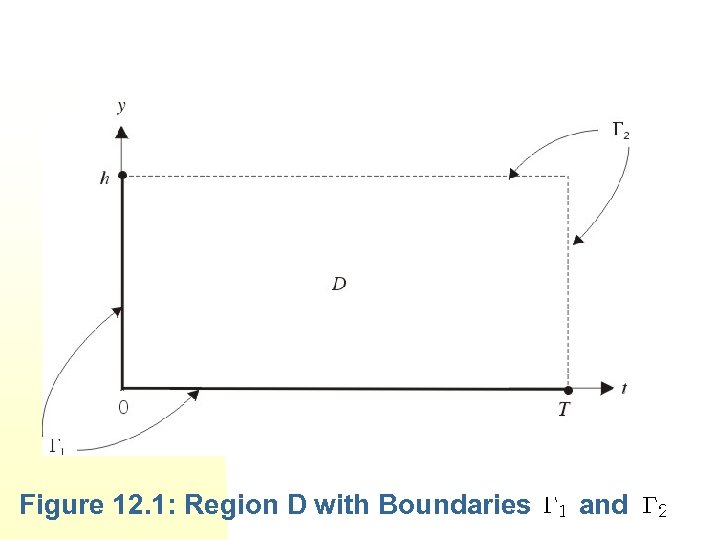
Figure 12. 1: Region D with Boundaries and

12. 2. 1 The Distributed Parameter Maximum Principle where xt= x/ t and xy= x/ y. The boundary conditions on are stated for the part of the boundary of D. which gives the consistency requirement in the sense that the price and the salvage value of a unit x(T, h) must agree.

We let u*(t, y) denote the optimal control function. Then the discounted parameter maximum principle requires that For all (t, y) D and all u . These general forms allow for the function F in (12. 2) to contain arguments such as x/ y, 2 x/ y 2, etc. It is also possible to consider controls on the boundary. In this case v(t) in (12. 33) will become a control variable.

12. 2. 2 The Cattle Ranching Problem Let t denote time and y denote the age of an animal. Let x(t, y) denote the number of cattle of age y on the ranch at time t. Let h be the age at maturity at which the cattle are slaughtered. Thus, the set [0, h] is the set of all possible ages of the cattle. Let u(t, y) be the rate at which y-aged cattle are bought at time t, where we agree that a negative value of u denotes a sale. Subtracting x(t, y) from both sides of (12. 42), dividing by t, and taking the limit as t 0, yields

The boundary and consistency conditions for x are given in (12. 32)-(12. 34). Here x 0(y) denotes the initial distribution of cattle at various ages, and v(t) is an exogenously specified breeding rate. Let P(t, y) be the purchase or sale price of a y-aged animal at time t. Let P(t, h)=Q(t) be the slaughter value at time t and let P(T, y)=S(y) be the salvage value of a y-aged animal at the horizon time T. The functions Q and S represent the proceeds of the cattle ranching business. Let C(y) be the feeding and corralling costs for a y-aged animal per unit of time. Let denote the goal level purchase rate of y-aged cattle at time t.

The deviation penalty cost is given by where q is a constant. subject to the boundary and consistency conditions (12. 38)-(12. 40).
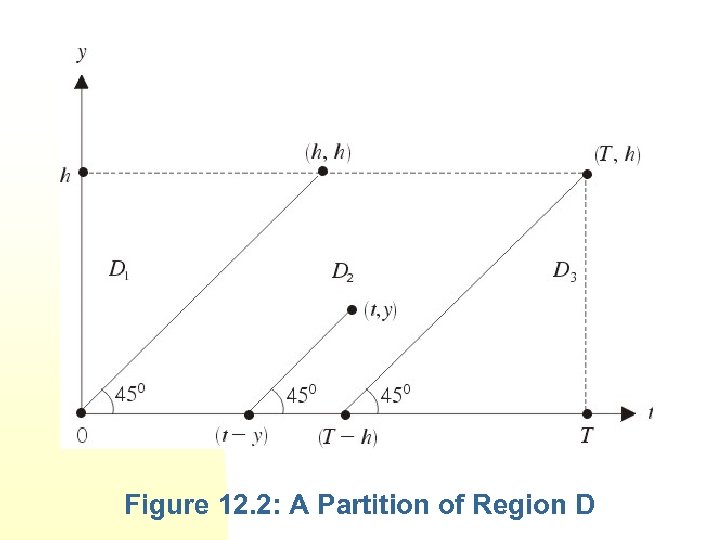
Figure 12. 2: A Partition of Region D

where g is an arbitrary one-variable function and k is a constant. We will use the boundary conditions to determine g and k. We substitute (12. 38) into (12. 48) and get This gives In the region D 1 D 2.

For region D 3, we use the condition (12. 39) on (T, y) in (12. 48) to obtain

(12. 50) in the region D 1 as the beginning game, which is completely characterized by the initial distribution x 0. Also the solution (12. 49) in region D 3 is the ending game, because in this region the animals do not mature, but must be sold at whatever their age is at the terminal time T.

12. 2. 3 Interpretation of the Adjoint Function An animal at age y at time t, where (t, y) is in D 1 D 2, will mature at time t-y+h. Its slaughter value at that time is Q(t-y+h). However, the total feeding and corralling cost in keeping the animal from its age y until it matures is given by Thus, (t, y) represents the net benefit obtained from having an animal at age y at time t. Interpret the optimal control u* in (12. 47). Whenever (t, y) > P(t, y) , we buy more than the goal level and when (t, y) < P(t, y), we buy less than the goal level.

12. 3 Impulse Control Example of an oil producer who pumps oil from a single well. where 1 is the starting stock of a new oil well.
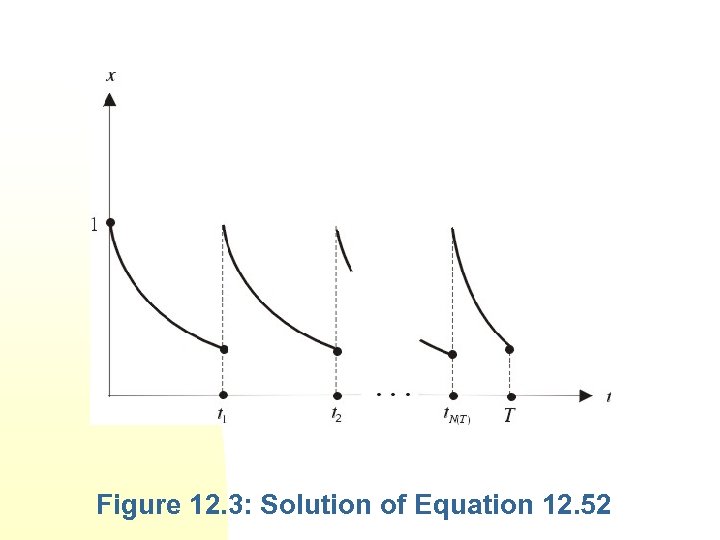
Figure 12. 3: Solution of Equation 12. 52

12. 3. 1 The Oil Driller’s Problem If t = ti , then , which means that we have abandoned the old well and drilled a new well with stock equal to v(ti). where P is the unit price of oil and Q is the drilling cost of drilling a well having an initial stock of 1.

12. 3. 2 The Maximum Principle for Impulse Optimal Control An impulse control variable v , and two associated functions. The first function is G(x, v, t), which represents the cost of profit associated with the impulse control. The sencond function is g(x, v, t), which represents the instantaneous finite change in the state variable when the impulse control is applied.

Impluse Hamiltonian function

When t 1 = 0 then the equality sign in (vii) should be replaced by a sign when i = 1. Note that condition (vii) involves the partial derivative of HI with respect to t. Thus, in autonomous problems, where condition (vii) means that the Hamiltonian H is continuous at those times where an impulse control is applied.

12. 3. 3 Solution of the Oil Driller’s Problem

Optimal impulse control at t 1 is After the drilling, (12. 70). which is given by shown in Figure 12. 4, which represent the condition prior to drilling. Figure 12. 4 is drawn under the assumption that
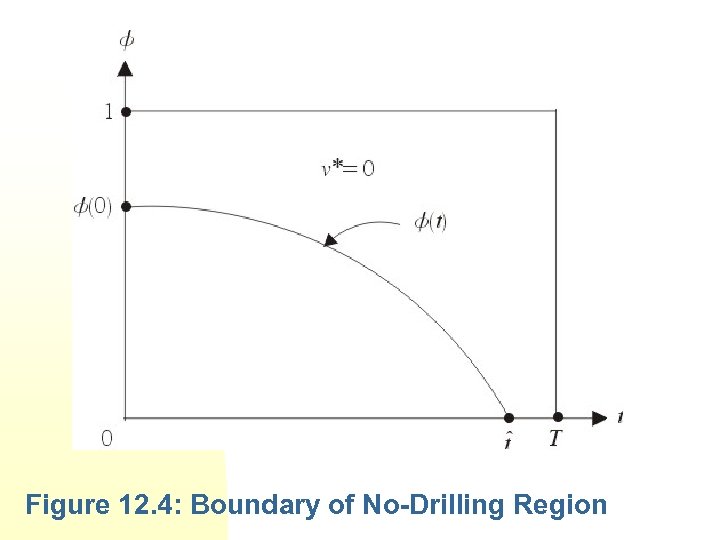
Figure 12. 4: Boundary of No-Drilling Region

From (12. 70), The curve is drawn in Figure 12. 5. BC of the curve lies in the no drilling region, which is above the curve as indicated in Figure 12. 5. The part AB of the curve is shown darkened and represents the drilling curve for the problem. The optimal state trajectory starts from x(0)=1 and decays exponentially at rate b until it hits the drilling curve AB at point Y.
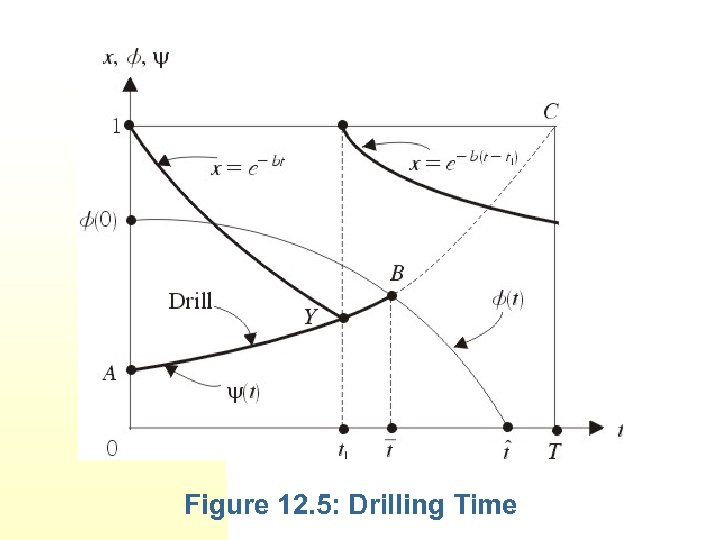
Figure 12. 5: Drilling Time
Figure 12. 6: Value of

This intersection point Y determines the drilling time t 1.

12. 3. 4: Machine Maintenance and Replacement T = the given terminal or horizon time, x(t) = the quality of the machine at time t, 0 x 1; a higher value of x denotes a better quality, u(t) = the ordinary control variable denoting the rate of maintenance at time t ; 0 u G < b/g, b = the constant rate at which quality deteriorates in the absence of any maintenance, g = the maintenance effectiveness coefficient, = the production rate per unit time per unit quality of the machine, K = the trade-in value per unit quality, i. e. , the old machine provides only a credit against the price of the new machine and it has no terminal salvage value,

C = the cost of new machine per unit quality; C > K, t 1 = the replacement time; for simplicity we assume at most one replacement to be optimal in the given horizon time; see Section 12. 3. 3, = the replacement variable, 0 1; represents a fraction of the old machine replaced by the same fraction of a new machine. This interpretation will make sense because we will show that v is either 0 or 1.

We have assumed that a fraction of a machine with quality x has a quality x. Furthermore, we note that the solution of the state equation will always satisfy 0 x 1, because of the assumption that u U b/g.

12. 3. 5 Application of the Impulse Maximum Principle

The solution of (12. 84) for t 1 < t T is The switching point Thus, is given by solving – 1+ g=0. provided the right-hand is in the interval (t 1, T]; otherwise set We can graph the optimal maintenance control in the interval (t 1, T] as in Figure 12. 7. Note that this is the optimal maintenance on the new machine. To find the optimal maintenance on the old machine, we need to obtain the value of (t) in the interval (t 1, T].

Figure 12. 7: Optimal Maintenance Policy

and compute the time which makes In plotting Figure 12. 8, we have assumed that 0< (0) <1. This is certainly the case, if T is not too large so that

As in the oil driller’s problem, we obtain (t) by using (12. 88). From (12. 92), we have v*(t 1)=1 and, therefore, (t 1) =K from (12. 85) and from (12. 83). Since g. K 1 from (12. 96), we have and, thus, u*(t 1)=0 from (12. 90). That is, zero maintenance is optimal on the old machine just before it is replaced. Since from (12. 97), we have from Figure 12. 7. That is, full maintenance is optimal on the new machine at the beginning.
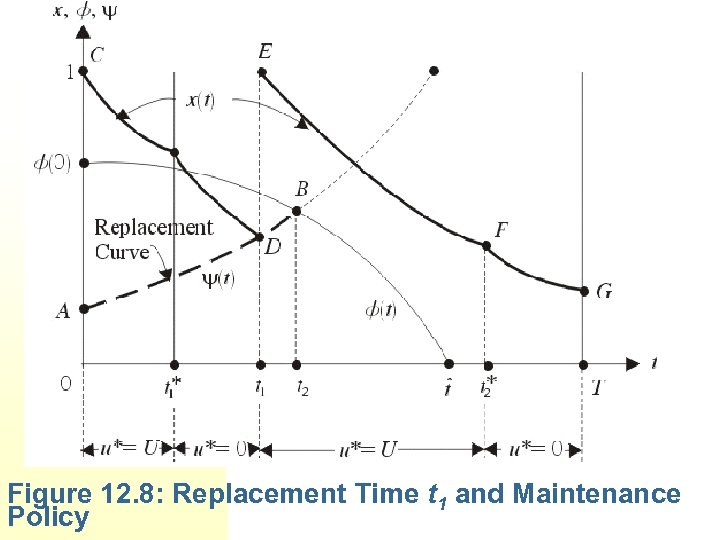
Figure 12. 8: Replacement Time t 1 and Maintenance Policy

AB represents the replacement curve. The optimal trajectory x*(t) is shown by CDEFG under the assumption that t 1 > 0 and t 1< t 2 , where t 2 is the intersection point of curves (t) and (t), as shown in Figure 12. 8. Figure 12. 9 has been drawn for a choice of the problem parameters such that t 1= t 2.
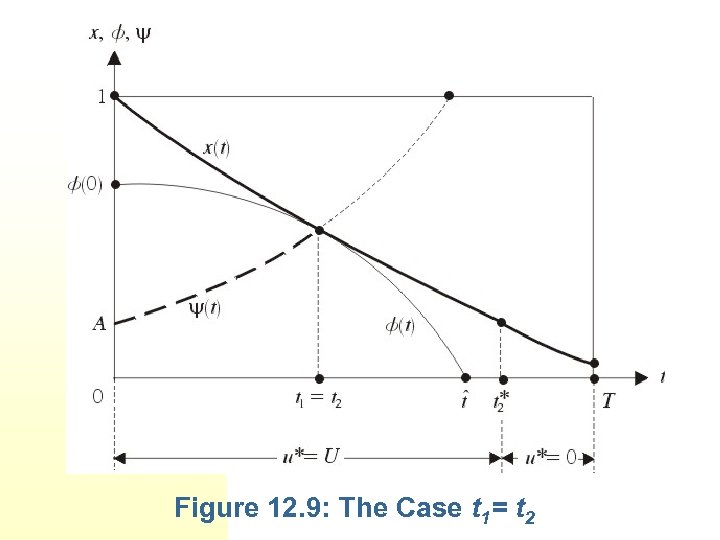
Figure 12. 9: The Case t 1= t 2

Using (t 1)=K obtained above and the adjoint equation (12. 84), we have Using (12. 100) in (12. 90), we can get u*(t), t [0, t 1]. and the switching point by solving – 1+ g=0. If 0, then the policy of no maintenance is optimal in the interval [0, t 1]. If > 0, the optimal maintenance policy for the old maintenance is In plotting Figure 12. 7 and 12. 8, we have assumed >0.
e61118f79a705065851c44f8a565bb15.ppt