e12b5101a2e8e636336394cafdcb532c.ppt
- Количество слайдов: 68

Chapter 12 Bond Selection 1

Malkiel’s Interest Rate Theorems u Definition u Theorem 1 u Theorem 2 u Theorem 3 u Theorem 4 u Theorem 5 2

Definition u Malkiel’s interest rate theorems provide information about how bond prices change as interest rates change u Any good portfolio manager knows Malkiel’s theorems 3

Theorem 1 u Bond prices move inversely with yields: • If interest rates rise, the price of an existing bond declines • If interest rates decline, the price of an existing bond increases 4

Theorem 2 u Bonds with longer maturities will fluctuate more if interest rates change u Long-term bonds have more interest rate risk 5
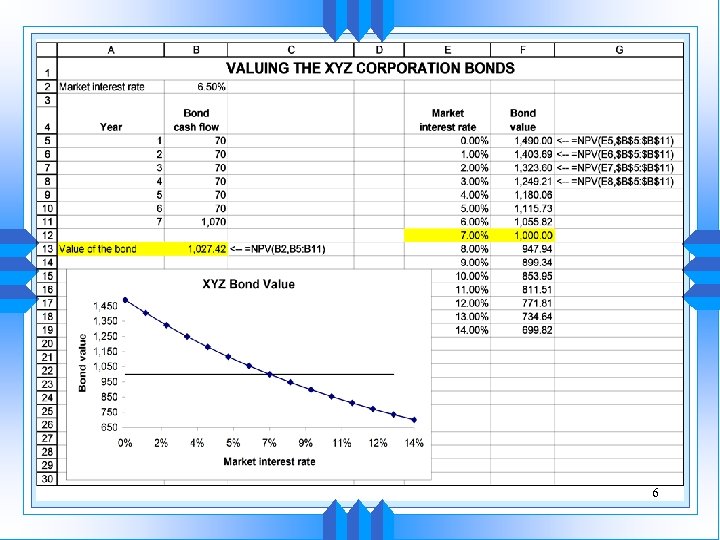
6

Theorem 3 u Higher coupon bonds have less interest rate risk u Money in hand is a sure thing while the present value of an anticipated future receipt is risky 7

Theorem 4 u When comparing two bonds, the relative importance of Theorem 2 diminishes as the maturities of the two bonds increase u. A given time difference in maturities is more important with shorter-term bonds 8

Theorem 5 u Capital gains from an interest rate decline exceed the capital loss from an equivalent interest rate increase 9

Duration as A Measure of Interest Rate Risk u The concept of duration u Calculating duration 10

The Concept of Duration u For a noncallable security: • Duration is the weighted average number of years necessary to recover the initial cost of the bond • Where the weights reflect the time value of money 11

The Concept of Duration (cont’d) u Duration is a direct measure of interest rate risk: • The higher the duration, the higher the interest rate risk 12

Calculating Duration u The traditional duration calculation: 13
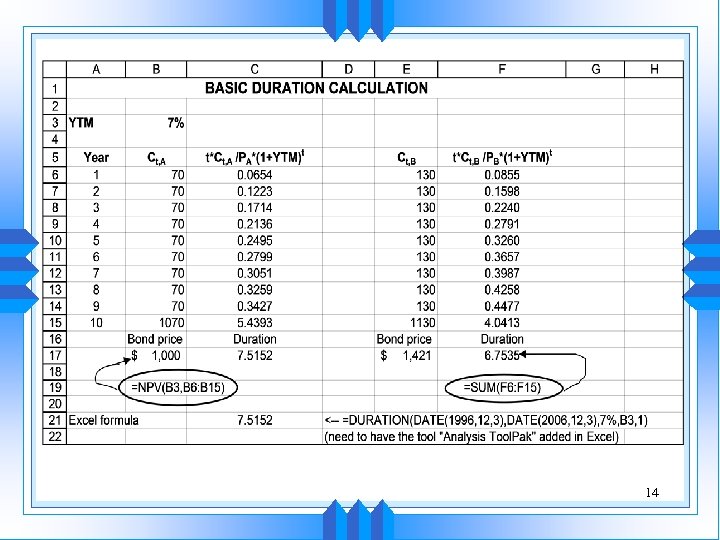
14

Calculating Duration (cont’d) u The closed-end formula for duration: 15

Calculating Duration (cont’d) Example Consider a bond that pays $100 annual interest and has a remaining life of 15 years. The bond currently sells for $985 and has a yield to maturity of 10. 20%. What is this bond’s duration? 16

Calculating Duration (cont’d) Example (cont’d) Solution: Using the closed-formula for duration: 17
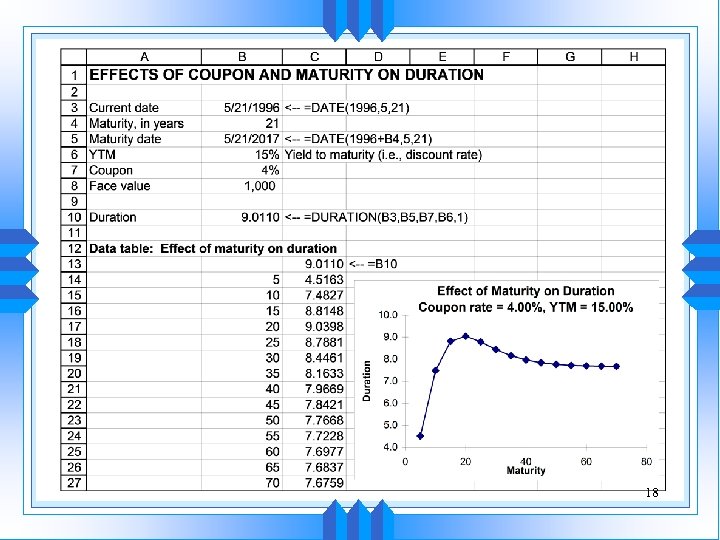
18
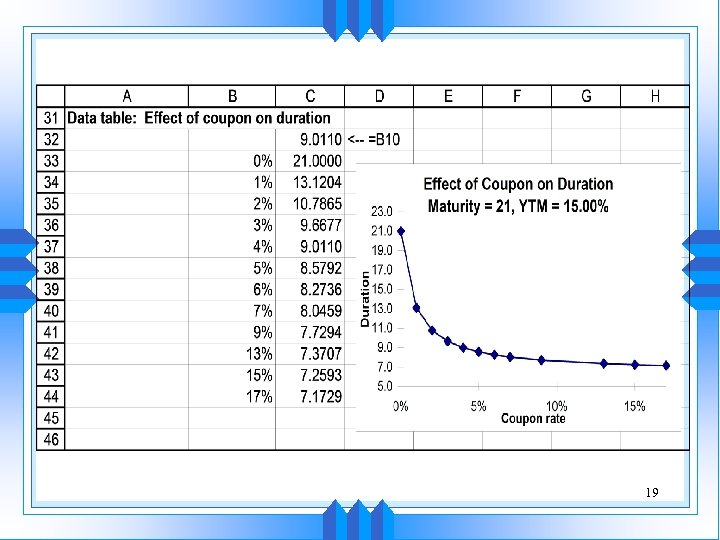
19

Bond Selection - Introduction u In most respects selecting the fixed-income components of a portfolio is easier than selecting equity securities u There are ways to make mistakes with bond selection 20

The Meaning of Bond Diversification u Introduction u Default risk u Dealing with the yield curve u Bond betas 21

Introduction u It is important to diversify a bond portfolio u Diversification of a bond portfolio is different from diversification of an equity portfolio u Two types of risk are important: • Default risk • Interest rate risk 22

Default Risk u Default risk refers to the likelihood that a firm will be unable to repay the principal and interest of a loan as agreed in the bond indenture • Equivalent to credit risk for consumers • Rating agencies such as S&P and Moody’s function as credit bureaus for credit issuers 23

Default Risk (cont’d) u To diversify default risk: • Purchase bonds from a number of different issuers • Do not purchase various bond issues from a single issuer – E. g. , Enron had 20 bond issues when it went bankrupt 24

Dealing With the Yield Curve u The yield curve is typically upward sloping • The longer a fixed-income security has until maturity, the higher the return it will have to compensate investors • The longer the average duration of a fund, the higher its expected return and the higher its interest rate risk 25

Dealing With the Yield Curve (cont’d) u The client and portfolio manager need to determine the appropriate level of interest rate risk of a portfolio 26

Bond Betas u The concept of bond betas: • States that the market prices a bond according to its level of risk relative to the market average • Has never become fully accepted • Measures systematic risk, while default risk and interest rate risk are more important 27

Choosing Bonds u Client psychology and bonds selling at a premium u Call risk u Constraints 28

Client Psychology and Bonds Selling at A Premium u Premium bonds held to maturity are expected to pay higher coupon rates than the market rate of interest u Premium bond held to maturity will decline in value toward par value as the bond moves towards its maturity date 29

Client Psychology & Bonds Selling at A Premium (cont’d) u Clients may not want to buy something they know will decline in value u There is nothing wrong with buying bonds selling at a premium 30

Call Risk u If a bond is called: • The funds must be reinvested • The fund manager runs the risk of having to make adjustments to many portfolios all at one time u There is no reason to exclude callable bonds categorically from a portfolio • Avoid making extensive use of a single callable bond issue 31

Constraints u Specifying return u Specifying grade u Specifying average maturity u Periodic income u Maturity timing u Socially responsible investing 32

Specifying Return u To increase the expected return on a bond portfolio: • Choose bonds with lower ratings • Choose bonds with longer maturities • Or both 33

Specifying Grade u. A legal list specifies securities that are eligible investments • E. g. , investment grade only u Portfolio managers take the added risk of noninvestment grade bonds only if the yield pickup is substantial 34

Specifying Grade (cont’d) u Conservative organizations will accept only U. S. government or AAA-rated corporate bonds u. A fund may be limited to no more than a certain percentage of non-AAA bonds 35

Specifying Average Maturity u Average maturity is a common bond portfolio constraint • The motivation is concern about rising interest rates • Specifying average duration would be an alternative approach 36

Periodic Income u Some funds have periodic income needs that allow little or not flexibility u Clients will want to receive interest checks frequently • The portfolio manager should carefully select the bonds in the portfolio 37

Maturity Timing u Maturity timing generates income as needed • Sometimes a manager needs to construct a bond portfolio that matches a particular investment horizon • E. g. , assemble securities to fund a specific set of payment obligations over the next ten years – Assemble a portfolio that generates income and principal repayments to satisfy the income needs 38

Socially Responsible Investing u Some clients will ask that certain types of companies not be included in the portfolio u Examples are nuclear power, military hardware, “vice” products 39

Example: Monthly Retirement Income u The problem u Unspecified constraints u Using S&P’s Bond Guide u Solving the problem 40

The Problem u. A client has: • Primary objective: growth of income • Secondary objective: income • $1, 100, 000 to invest • Inviolable income needs of $4, 000 per month 41

The Problem (cont’d) u You decide: • To invest the funds 50 -50 between common stocks and debt securities • To invest in ten common stock in the equity portion (see next slide) – You incur $1, 500 in brokerage commissions 42
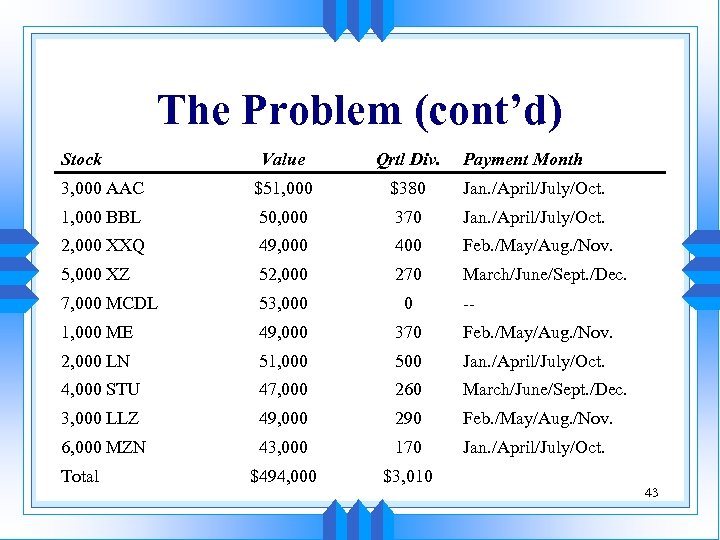
The Problem (cont’d) Stock Value Qrtl Div. 3, 000 AAC $51, 000 $380 Jan. /April/July/Oct. 1, 000 BBL 50, 000 370 Jan. /April/July/Oct. 2, 000 XXQ 49, 000 400 Feb. /May/Aug. /Nov. 5, 000 XZ 52, 000 270 March/June/Sept. /Dec. 7, 000 MCDL 53, 000 0 1, 000 ME 49, 000 370 Feb. /May/Aug. /Nov. 2, 000 LN 51, 000 500 Jan. /April/July/Oct. 4, 000 STU 47, 000 260 March/June/Sept. /Dec. 3, 000 LLZ 49, 000 290 Feb. /May/Aug. /Nov. 6, 000 MZN 43, 000 170 Jan. /April/July/Oct. $494, 000 $3, 010 Total Payment Month -- 43

The Problem (cont’d) u Characteristics of the fund: • Quarterly dividends total $3, 001 ($12, 004 annually) • The dividend yield on the equity portfolio is 2. 44% • Total annual income required is $48, 000 or 4. 36% of fund • Bonds need to have a current yield of at least 6. 28% 44

Unspecified Constraints u The task is meeting the minimum required expected return with the least possible risk • You don’t want to choose CC-rated bonds • You don’t want the longest maturity bonds you can find 45

Using S&P’s Bond Guide u Figure 11 -4 is an excerpt from the Bond Guide: • Indicates interest payment dates, coupon rates, and issuer • Provides S&P ratings • Provides current price, current yield 46

Using S&P’s Bond Guide (cont’d) 47

Solving the Problem u Setup u Dealing with accrued interest and commissions u Choosing the bonds u Overspending u What about convertible bonds? 48

Setup u You have two constraints: • Include only bonds rated BBB or higher • Keep the average maturities below fifteen years u Set up a worksheet that enables you to pick bonds to generate exactly $4, 000 per month (see next slide) 49
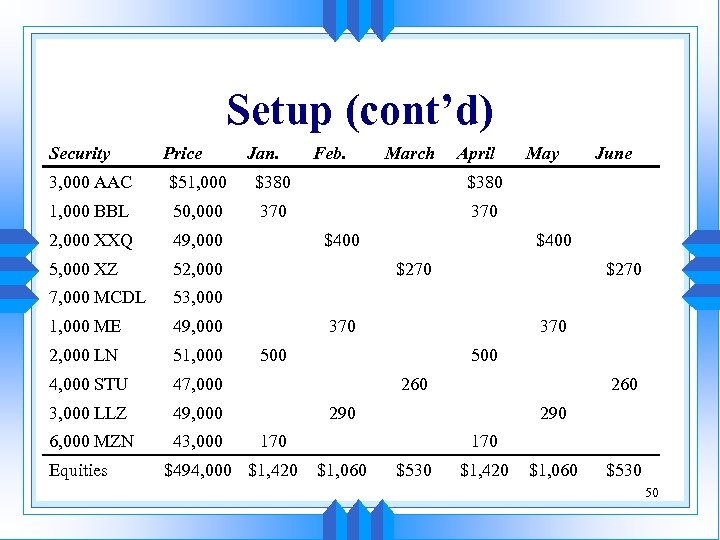
Setup (cont’d) Security Price Jan. Feb. March April 3, 000 AAC $51, 000 $380 50, 000 370 2, 000 XXQ 49, 000 5, 000 XZ 52, 000 7, 000 MCDL 53, 000 1, 000 ME 49, 000 2, 000 LN 51, 000 4, 000 STU 47, 000 3, 000 LLZ 49, 000 6, 000 MZN 43, 000 June $380 1, 000 BBL May Equities $400 $270 370 500 260 290 170 $494, 000 $1, 420 170 $1, 060 $530 $1, 420 $1, 060 $530 50

Dealing With Accrued Interest and Commissions u Bond prices are typically quoted on a net basis (already include commissions) u Calculate accrued interest using the midterm heuristic • Assume every bond’s accrued interest is half of one interest check 51

Choosing the Bonds u The • • following slide shows one possible solution: Stock cost: $494, 000 Bond cost: $557, 130 Accrued interest: $9, 350 Stock commissions: $1, 500 52
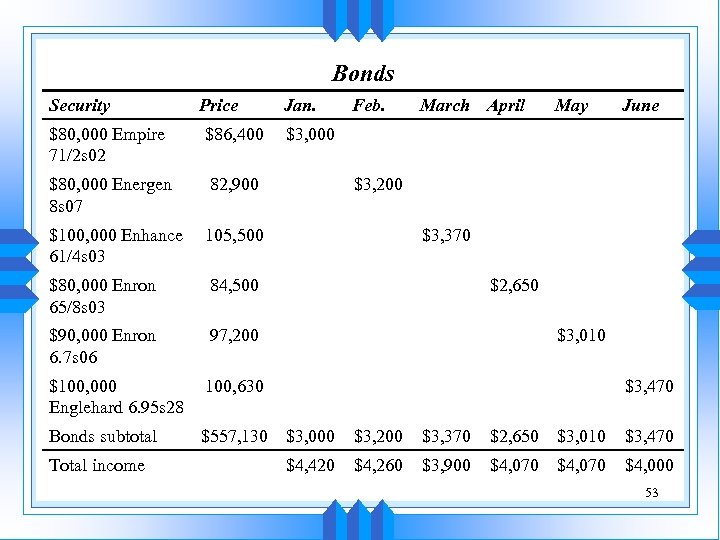
Bonds Security Price Jan. Feb. March April May June $80, 000 Empire 71/2 s 02 $86, 400 $80, 000 Energen 8 s 07 82, 900 $100, 000 Enhance 61/4 s 03 105, 500 $80, 000 Enron 65/8 s 03 84, 500 $90, 000 Enron 6. 7 s 06 97, 200 $100, 000 Englehard 6. 95 s 28 100, 630 Bonds subtotal $557, 130 $3, 000 $3, 200 $3, 370 $2, 650 $3, 010 $3, 470 $4, 420 $4, 260 $3, 900 $4, 070 $4, 000 Total income $3, 000 $3, 200 $3, 370 $2, 650 $3, 010 $3, 470 53

Overspending u The total of all costs associated with the portfolio should not exceed the amount given to you by the client to invest u The money the client gives you establishes another constraint 54

What About Convertible Bonds? u Convertible bonds can be included in a portfolio • Useful for a growth of income objective • People buy convertible bonds in hopes of price appreciation • Useful if you otherwise meet your income constraints 55

Immunization Strategies u. A portfolio of bonds is said to be immunized (from interest rate risk) if its payoff at some future date is independent of the future levels of interest rates. u Immunization is closely related to the concept of duration. 56

u Immunization consists of matching the duration of the portfolio’s assets and liabilities (obligations). u Suppose a firm has a future obligation Q. The prevailing interest rate is r, and the liability is N periods away. u The present value of this liability is denoted by V 0=Q/(1+r)N. 57

u Now suppose that the firm is currently hedging this liability with a bond whose value VB = V 0 and whose coupon payments are denoted by P 1, …, PM. u We thus have: 58

u Suppose now that interest rates change from r to r+Dr. The new values of the future obligation and of the bond are: 59

u Rearranging terms and recalling that V 0=VB yields the following expression: u The left-hand side represents the duration of the bond, while the right-hand side represents the duration of the obligation (Since the obligation consisted of only one payment, the duration is its maturity). 60

u In conclusion, in order for a portfolio to be immunized, you need to have: u DURATIONASSETS = DURATIONLIABILITIES u Caveat: this works only if the interest rates of various maturities all change in the same manner, i. e. if the yield curve shifts upward or downward in a parallel shift. 61

Immunization Example u You need to immunize an obligation whose present value V 0 is $1, 000. The payment is to be made 10 years from now, and the current interest rate is 6%. The payment is thus the future value of 1, 000 at 6%, therefore it is: 1, 000(1. 06)10 = $1, 790. 85 u The Excel spreadsheet on the next slide shows three bonds that you have at your disposition to immunize the liability. 62
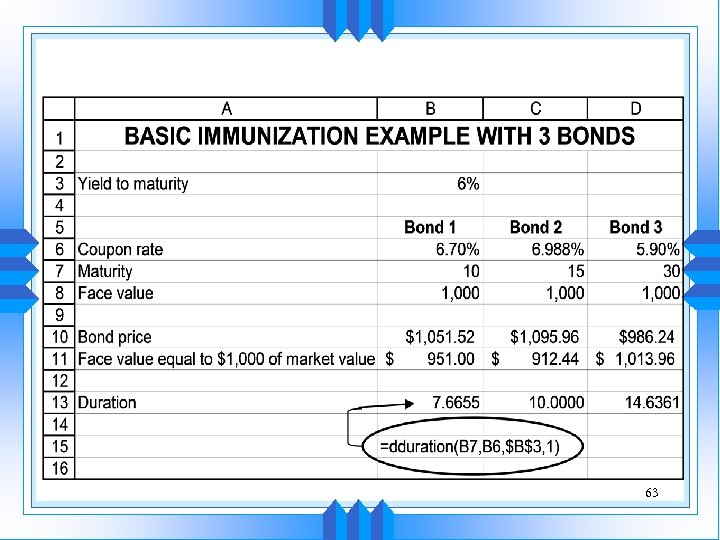
63
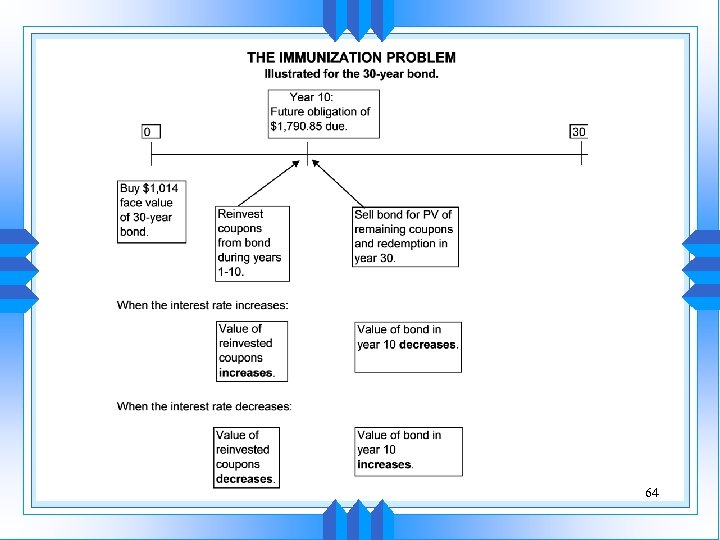
64

Values 10 years later, assuming interest rates do not change (The goal of getting $1, 790. 85 is still met) 65

Values 10 years later, assuming interest rates change to 5% right after we buy the bonds (The goal of getting $1, 790. 85 is not met by Bond 1 anymore) 66

Observations u If interest rates go down to 5%, Bond 1 does not meet the requirement anymore. u Bond 3, on the other hand, exceeds the payment that must be made in year 10. u The ability of Bond 2 to meet the obligation is barely affected. Why? Because its duration is 10 years, exactly matching the duration of the liability. Pick Bond 2. 67
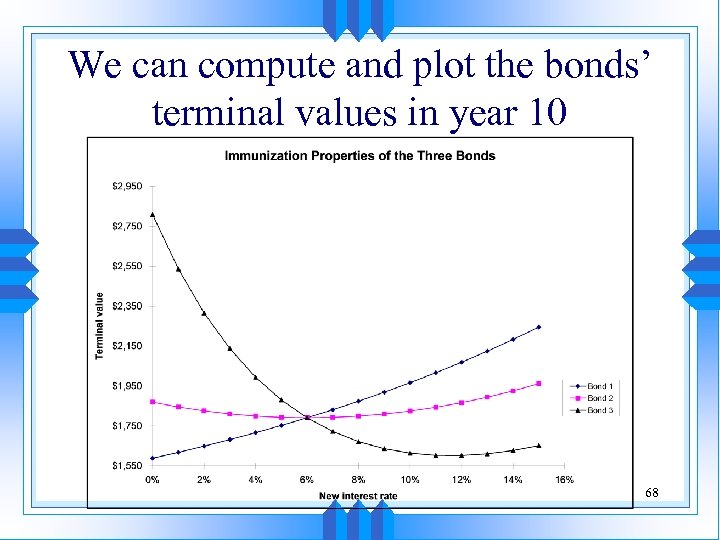
We can compute and plot the bonds’ terminal values in year 10 68
e12b5101a2e8e636336394cafdcb532c.ppt