Chapter 11 The Order Up-To Model Medtronic s

Chapter 11: The Order Up-To Model

Medtronic’s In. Sync pacemaker supply chain and objectives ü Look at problem from two persopectives … ä One distribution center (DC) in Mounds View, MN. ä About 500 sales territories throughout the country. ä Consider Susan Magnotto’s territory in Madison, Wisconsin. ü Objective: ä Because the gross margins are high, develop a system to minimize inventory investment while maintaining a very high service target, e. g. , a 99. 9% in-stock probability or a 99. 9% fill rate.

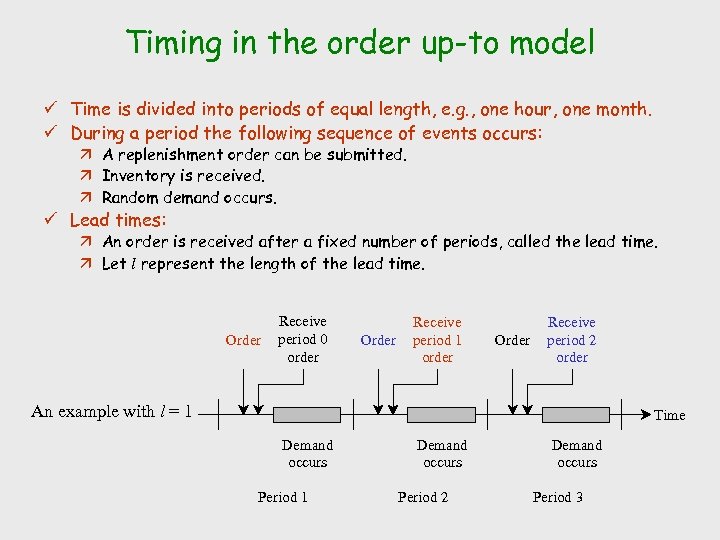Timing in the order up-to model ü Time is divided into periods of equal length, e. g. , one hour, one month. ü During a period the following sequence of events occurs: ä A replenishment order can be submitted. ä Inventory is received. ä Random demand occurs. ü Lead times: ä An order is received after a fixed number of periods, called the lead time. ä Let l represent the length of the lead time. Order Receive period 0 order Order Receive period 1 order Order Receive period 2 order An example with l = 1 Time Demand occurs Period 1 Demand occurs Period 2 Demand occurs Period 3

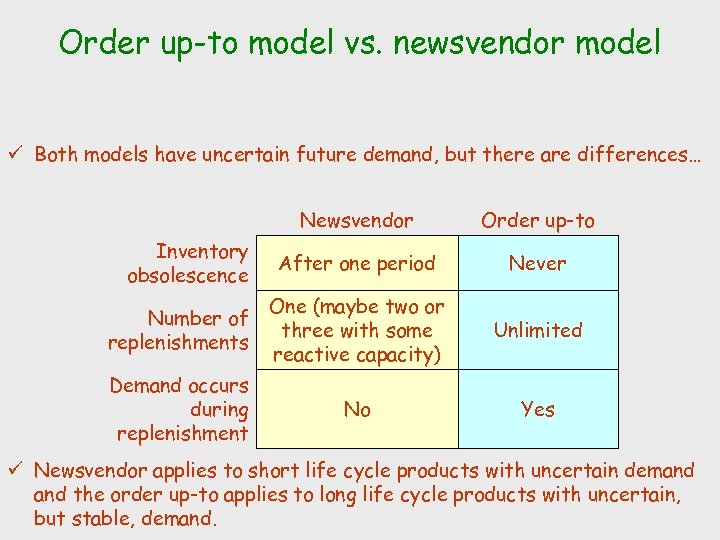Order up-to model vs. newsvendor model ü Both models have uncertain future demand, but there are differences… Newsvendor Order up-to After one period Never Number of replenishments One (maybe two or three with some reactive capacity) Unlimited Demand occurs during replenishment No Yes Inventory obsolescence ü Newsvendor applies to short life cycle products with uncertain demand the order up-to applies to long life cycle products with uncertain, but stable, demand.

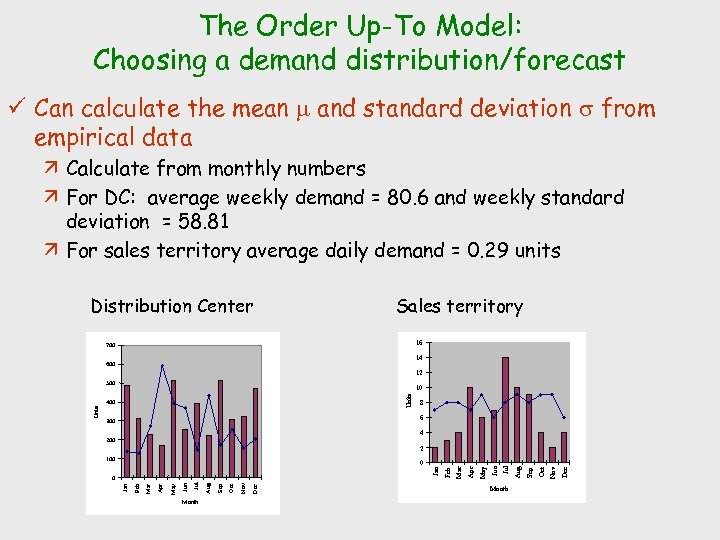The Order Up-To Model: Choosing a demand distribution/forecast ü Can calculate the mean m and standard deviation s from empirical data ä Calculate from monthly numbers ä For DC: average weekly demand = 80. 6 and weekly standard deviation = 58. 81 ä For sales territory average daily demand = 0. 29 units Distribution Center Sales territory 16 700 14 600 12 Units 10 400 8 6 300 4 200 Nov Dec Sep Oct Jul Aug Apr May Mar Jan Jun Month Dec Oct Nov Sep Jul Month Aug Jun Apr May Mar Jan 0 0 Feb 2 100 Feb Units 500

The Order Up-To Model: Model design and implementation

Order up-to model definitions ü On-order inventory [a. k. a. pipeline inventory] = the number of units that have been ordered but have not been received. ü On-hand inventory = the number of units physically in inventory ready to serve demand. ü Backorder = the total amount of demand that has not been satisfied: ä All backordered demand is eventually filled, i. e. , there are no lost sales. ü Inventory level = On-hand inventory - Backorder. ü Inventory position = On-order inventory + Inventory level. ü Order up-to level, S ä the maximum inventory position we allow. ä sometimes called the base stock level.

Order up-to model implementation ü Each period’s order quantity = S – Inventory position ä Suppose S = 4. ä If a period begins with an inventory position = 1, then three units are ordered. (4 – 1 = 3 ) ä If a period begins with an inventory position = -3, then seven units are ordered (4 – (-3) = 7) ü A period’s order quantity = the previous period’s demand: ä Suppose S = 4. ä If demand were 10 in period 1, then the inventory position at the start of period 2 is 4 – 10 = -6, which means 10 units are ordered in period 2. ä The order up-to model is a pull system because inventory is ordered in response to demand. ä The order up-to model is sometimes referred to as a 1 -for-1 ordering policy.

The Order Up-To Model: Performance measures

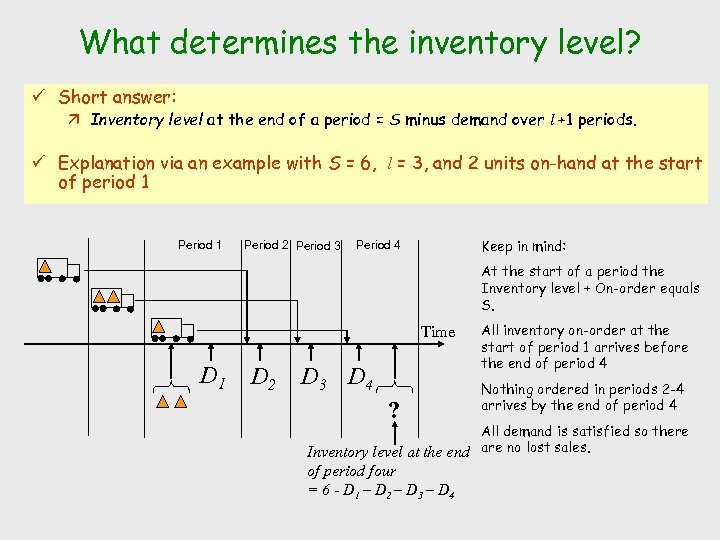What determines the inventory level? ü Short answer: ä Inventory level at the end of a period = S minus demand over l +1 periods. ü Explanation via an example with S = 6, l = 3, and 2 units on-hand at the start of period 1 Period 2 Period 3 Keep in mind: Period 4 At the start of a period the Inventory level + On-order equals S. Time D 1 D 2 D 3 D 4 ? All inventory on-order at the start of period 1 arrives before the end of period 4 Nothing ordered in periods 2 -4 arrives by the end of period 4 All demand is satisfied so there Inventory level at the end are no lost sales. of period four = 6 - D 1 – D 2 – D 3 – D 4

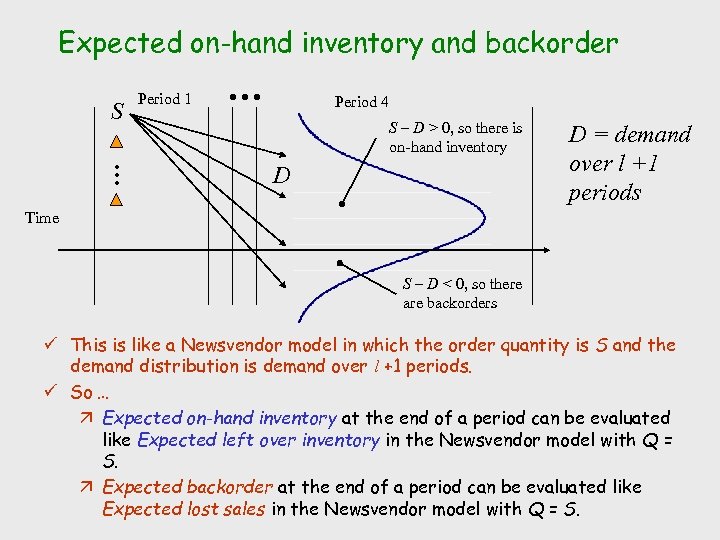Expected on-hand inventory and backorder … S Period 1 … Period 4 S – D > 0, so there is on-hand inventory D D = demand over l +1 periods Time S – D < 0, so there are backorders ü This is like a Newsvendor model in which the order quantity is S and the demand distribution is demand over l +1 periods. ü So … ä Expected on-hand inventory at the end of a period can be evaluated like Expected left over inventory in the Newsvendor model with Q = S. ä Expected backorder at the end of a period can be evaluated like Expected lost sales in the Newsvendor model with Q = S.

Stockout and in-stock probabilities, on-order inventory and fill rate ü The stockout probability is the probability at least one unit is backordered in a period: ü The in-stock probability is the probability all demand is filled in a period: ü Expected on-order inventory = Expected demand over one period x lead time ä This comes from Little’s Law. Note that it equals the expected demand over l periods, not l +1 periods. ü The fill rate is the fraction of demand within a period that is NOT backordered:

Demand over l +1 periods ü DC: ä The period length is one week, the replenishment lead time is three weeks, l =3 ä Assume demand is normally distributed: ä Mean weekly demand is 80. 6 (from demand data) ä Standard deviation of weekly demand is 58. 81 (from demand data) ä Expected demand over l +1 weeks is (3 + 1) x 80. 6 = 322. 4 ä Standard deviation of demand over l +1 weeks is ü Susan’s territory: ä The period length is one day, the replenishment lead time is one day, l =1 ä Assume demand is Poisson distributed: ä Mean daily demand is 0. 29 (from demand data) ä Expected demand over l +1 days is 2 x 0. 29 = 0. 58 ä Recall, the Poisson is completely defined by its mean (and the standard deviation is always the square root of the mean)

DC’s Expected backorder assuming S = 625 ü Expected backorder is analogous to the Expected lost sales in the Newsvendor model: ä Suppose S = 625 at the DC ä Normalize the order up-to level: ä Lookup L(z) in the Standard Normal Loss Function Table: L(2. 57)=0. 0016 ä Convert expected lost sales, L(z), for the standard normal into the expected backorder with the actual normal distribution that represents demand over l+1 periods: ä Therefore, if S = 625, then on average there are 0. 19 backorders at the end of any period at the DC.

Other DC performance measures with S = 625 ü So 99. 76% of demand is filled immediately (i. e. , without being backordered) ä (Note for below: inventory level + backorder = on hand) ü So on average there are 302. 8 units on-hand at the end of a period. ü So there are 241. 8 units on-order at any given time.

Performance measures in Susan’s territory: ~~FYI but will not be covered on Exam ü Look up in the Poisson Loss Function Table expected backorders for a Poisson distribution with a mean equal to expected demand over l+1 periods: ü Suppose S = 3: ä Expected backorder = 0. 00335 ä In-stock = 99. 702% ä Fill rate = 1 – 0. 00335 / 0. 29 = 98. 84% ä Expected on-hand = S – demand over l+1 periods + backorder = 3 – 0. 58 + 0. 00335 = 2. 42 ä Expected on-order inventory = Demand over the lead time = 0. 29

Problem 11. 1 A furniture store sells study desks with normally distributed demand. The mean = 40 and the standard deviation = 20. The lead time is 2 weeks and inventory replenishments are ordered weekly. a) If S = 220 and your inventory = 100 with 85 desks on order, how many desks will you order? (35) b) Suppose S = 220 and you are about to place an order and your inventory level – 160 with 65 desks on order. How many desks will you order? (order 0)

The Order Up-To Model: Choosing an order up-to level, S, to meet a service target

Choose S to hit a target in-stock with normally distributed demand ü Suppose the target in-stock probability at the DC is 99. 9%: ä From the Standard Normal Distribution Function Table, F(3. 08)=0. 9990 ä So we choose z = 3. 08 ä To convert z into an order up-to level: ä Note that m and s are the parameters of the normal distribution that describes demand over l + 1 periods.

Problem 11. 1 A furniture store sells study desks with normally distributed demand. The mean = 40 and the standard deviation = 20. The lead time is 2 weeks and inventory replenishments are ordered weekly. c) What is the optimal order-up-to level if you want to target a 98% in stock probability? (191. 14)

Choose S to hit a target fill rate with normally distributed demand ü Find the S that yields a 99. 9% fill rate for the DC. ü Step 1: Evaluate the target lost sales ä note 1 period in the numerator and l + 1 periods in the denominator ü Step 2: Find the z that generates that target lost sales in the Standard Normal Loss Function Table: ä L(2. 81) = L(2. 82) = L(2. 83) = L(2. 84) = 0. 0007 ä Choose z = 2. 84 to be conservative (higher z means higher fill rate) ü Step 3: Convert z into the order up-to level:

Problem 11. 1 A furniture store sells study desks with normally distributed demand. The mean = 40 and the standard deviation = 20. The lead time is 2 weeks and inventory replenishments are ordered weekly. d) What is the optimal order-up-to level if you want to target a 98% fill rate? (S = 175. 77)

The Order Up-To Model: Appropriate service levels

Justifying a service level via cost minimization ü Let h equal the holding cost per unit period ä e. g. if p is the retail price, the gross margin is 75%, the annual holding cost is 35% and there are 260 days per year, then h = p x (1 -0. 75) x 0. 35 / 260 = 0. 000337 x p ü Let b equal the penalty per unit backordered ä e. g. , let the penalty equal the 75% gross margin, then b = 0. 75 x p ü “Too much-too little” challenge: ä If S is too high, then there are holding costs, Co = h ä If S is too low, then there are backorders, Cu = b ü Cost minimizing order up-to level satisfies ü Optimal in-stock probability is 99. 96% because

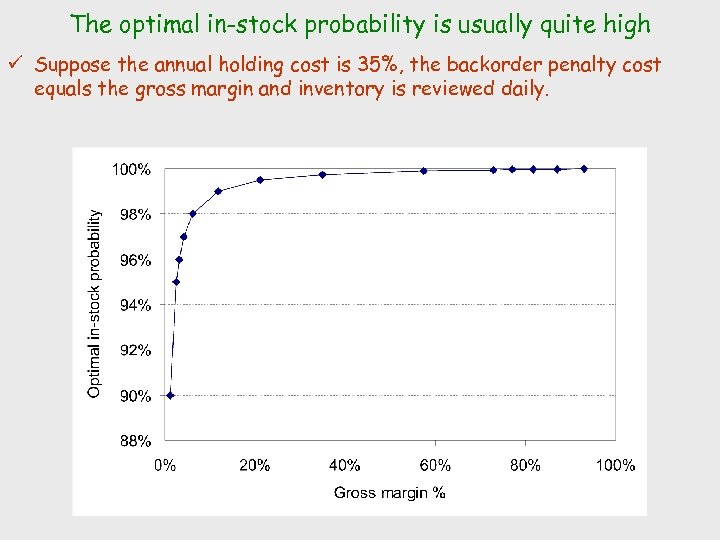The optimal in-stock probability is usually quite high ü Suppose the annual holding cost is 35%, the backorder penalty cost equals the gross margin and inventory is reviewed daily.

Problem 11. 1 A furniture store sells study desks with normally distributed demand. The mean = 40 and the standard deviation = 20. The lead time is 2 weeks and inventory replenishments are ordered weekly. e) Suppose S = 120. What is the expected on-hand inventory? (13. 82) f) Suppose S = 200. What is the fill rate? (99. 69%) g) Suppose you want to maintain a 95% in-stock probability. What is the expected fill-rate? (98. 22%)

The Order Up-To Model: Controlling ordering costs

Impact of the period length ü Increasing the period length leads to larger and less frequent orders: ä The average order quantity = expected demand in a single period. ä The frequency of orders approximately equals 1/length of period. ä See “saw tooth” diagrams in the text ü Suppose there is a cost to hold inventory and a cost to submit each order (independent of the quantity ordered)… ü … then there is a tradeoff between carrying little inventory (short period lengths) and reducing ordering costs (long period lengths)

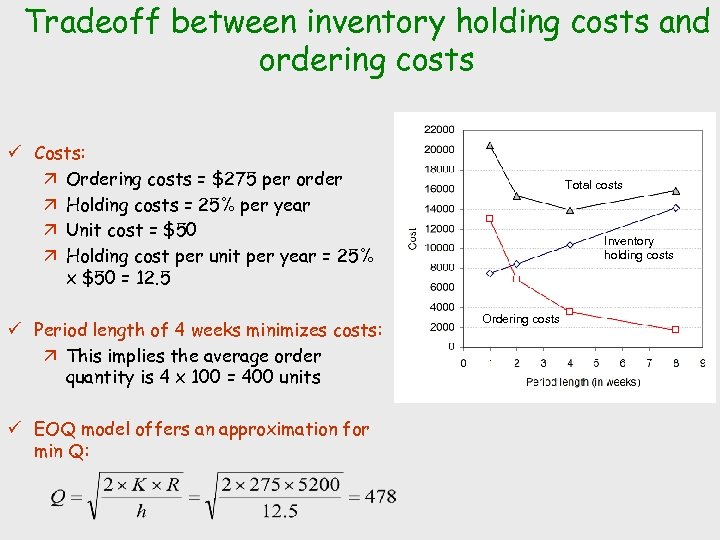Tradeoff between inventory holding costs and ordering costs ü Costs: ä Ordering costs = $275 per order ä Holding costs = 25% per year ä Unit cost = $50 ä Holding cost per unit per year = 25% x $50 = 12. 5 ü Period length of 4 weeks minimizes costs: ä This implies the average order quantity is 4 x 100 = 400 units ü EOQ model offers an approximation for min Q: Total costs Inventory holding costs Ordering costs

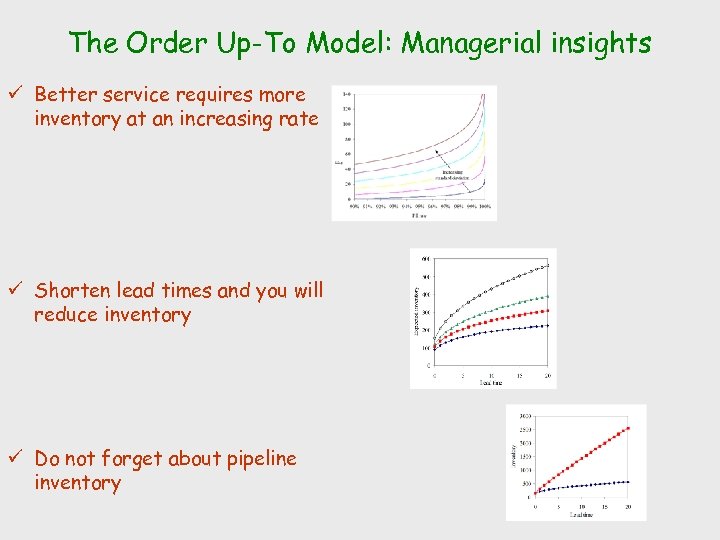The Order Up-To Model: Managerial insights ü Better service requires more inventory at an increasing rate ü Shorten lead times and you will reduce inventory ü Do not forget about pipeline inventory

Order up-to model summary ü The order up-to model is appropriate for products with random demand but many replenishment opportunities. ü Expected inventory and service are controlled via the order up-to level: ä The higher the order up-to level the greater the expected inventory and the better the service (either in-stock probability or fill rate). ü The key factors that determine the amount of inventory needed are… ä The length of the replenishment lead time. ä The desired service level (fill rate or in-stock probability). ä Demand uncertainty. ü When inventory obsolescence is not an issue, the optimal service level is generally quite high.

Problem 11. 1 A furniture store sells study desks with normally distributed demand. The mean = 40 and the standard deviation = 20. The lead time is 2 weeks and inventory replenishments are ordered weekly. a) If S = 220 and your inventory = 100 with 85 desks on order, how many desks will you order? (35) b) Suppose S = 220 and you are about to place an order and your inventory level – 160 with 65 desks on order. How many desks will you order? (order 0) c) What is the optimal order-up-to level if you want to target a 98% in stock probability? (191. 14) d) What is the optimal order-up-to level if you want to target a 98% fill rate? (S = 175. 77) e) Suppose S = 120. What is the expected on-hand inventory? (13. 82) f) Suppose S = 200. What is the fill rate? (99. 69%) g) Suppose you want to maintain a 95% in-stock probability. What is the expected fill-rate? (98. 22%)