4bf11e5e5b85b4efd7e70b5e03cc30b5.ppt
- Количество слайдов: 198
 Chapter 11 Inferences on Two Samples © 2010 Pearson Prentice Hall. All rights reserved
Chapter 11 Inferences on Two Samples © 2010 Pearson Prentice Hall. All rights reserved
 Section 11. 1 Inference about Two Means: Dependent Samples © 2010 Pearson Prentice Hall. All rights reserved
Section 11. 1 Inference about Two Means: Dependent Samples © 2010 Pearson Prentice Hall. All rights reserved
 Objectives 1. Distinguish between independent and dependent sampling 2. Test hypotheses regarding matched-pairs data 3. Construct and interpret confidence intervals about the population mean difference of matched-pairs data © 2010 Pearson Prentice Hall. All rights reserved 104
Objectives 1. Distinguish between independent and dependent sampling 2. Test hypotheses regarding matched-pairs data 3. Construct and interpret confidence intervals about the population mean difference of matched-pairs data © 2010 Pearson Prentice Hall. All rights reserved 104
 Objective 1 • Distinguish between Independent and Dependent Sampling © 2010 Pearson Prentice Hall. All rights reserved 105
Objective 1 • Distinguish between Independent and Dependent Sampling © 2010 Pearson Prentice Hall. All rights reserved 105
 A sampling method is independent when the individuals selected for one sample do not dictate which individuals are to be in a second sample. A sampling method is dependent when the individuals selected to be in one sample are used to determine the individuals to be in the second sample. Dependent samples are often referred to as matched-pairs samples. © 2010 Pearson Prentice Hall. All rights reserved 106
A sampling method is independent when the individuals selected for one sample do not dictate which individuals are to be in a second sample. A sampling method is dependent when the individuals selected to be in one sample are used to determine the individuals to be in the second sample. Dependent samples are often referred to as matched-pairs samples. © 2010 Pearson Prentice Hall. All rights reserved 106
 Parallel Example 1: Distinguish between Independent and Dependent Sampling For each of the following, determine whether the sampling method is independent or dependent. a) A researcher wants to know whether the price of a one night stay at a Holiday Inn Express is less than the price of a one night stay at a Red Roof Inn. She randomly selects 8 towns where the location of the hotels is close to each other and determines the price of a one night stay. b) A researcher wants to know whether the “state” quarters (introduced in 1999) have a mean weight that is different from “traditional” quarters. He randomly selects 18 “state” quarters and 16 “traditional” quarters and compares their weights. © 2010 Pearson Prentice Hall. All rights reserved 107
Parallel Example 1: Distinguish between Independent and Dependent Sampling For each of the following, determine whether the sampling method is independent or dependent. a) A researcher wants to know whether the price of a one night stay at a Holiday Inn Express is less than the price of a one night stay at a Red Roof Inn. She randomly selects 8 towns where the location of the hotels is close to each other and determines the price of a one night stay. b) A researcher wants to know whether the “state” quarters (introduced in 1999) have a mean weight that is different from “traditional” quarters. He randomly selects 18 “state” quarters and 16 “traditional” quarters and compares their weights. © 2010 Pearson Prentice Hall. All rights reserved 107
 Solution a) The sampling method is dependent since the 8 Holiday Inn Express hotels can be matched with one of the 8 Red Roof Inn hotels by town. b) The sampling method is independent since the “state” quarters which were sampled had no bearing on which “traditional” quarters were sampled. © 2010 Pearson Prentice Hall. All rights reserved 108
Solution a) The sampling method is dependent since the 8 Holiday Inn Express hotels can be matched with one of the 8 Red Roof Inn hotels by town. b) The sampling method is independent since the “state” quarters which were sampled had no bearing on which “traditional” quarters were sampled. © 2010 Pearson Prentice Hall. All rights reserved 108
 Objective 2 • Test Hypotheses Regarding Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 109
Objective 2 • Test Hypotheses Regarding Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 109
 “In Other Words” Statistical inference methods on matched-pairs data use the same methods as inference on a single population mean with unknown, except that the differences are analyzed. © 2010 Pearson Prentice Hall. All rights reserved 110
“In Other Words” Statistical inference methods on matched-pairs data use the same methods as inference on a single population mean with unknown, except that the differences are analyzed. © 2010 Pearson Prentice Hall. All rights reserved 110
 Testing Hypotheses Regarding the Difference of Two Means Using a Matched-Pairs Design To test hypotheses regarding the mean difference of matched-pairs data, the following must be satisfied: 1. the sample is obtained using simple random sampling 2. the sample data are matched pairs, 3. the differences are normally distributed with no outliers or the sample size, n, is large (n ≥ 30). © 2010 Pearson Prentice Hall. All rights reserved 111
Testing Hypotheses Regarding the Difference of Two Means Using a Matched-Pairs Design To test hypotheses regarding the mean difference of matched-pairs data, the following must be satisfied: 1. the sample is obtained using simple random sampling 2. the sample data are matched pairs, 3. the differences are normally distributed with no outliers or the sample size, n, is large (n ≥ 30). © 2010 Pearson Prentice Hall. All rights reserved 111
 Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways, where d is the population mean difference of the matched-pairs data. © 2010 Pearson Prentice Hall. All rights reserved 112
Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways, where d is the population mean difference of the matched-pairs data. © 2010 Pearson Prentice Hall. All rights reserved 112
 Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 113
Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 113
 Step 3: Compute the test statistic which approximately follows Student’s t-distribution with n-1 degrees of freedom. The values of and sd are the mean and standard deviation of the differenced data. © 2010 Pearson Prentice Hall. All rights reserved 114
Step 3: Compute the test statistic which approximately follows Student’s t-distribution with n-1 degrees of freedom. The values of and sd are the mean and standard deviation of the differenced data. © 2010 Pearson Prentice Hall. All rights reserved 114
 Classical Approach Step 4: Use Table VI to determine the critical value using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 115
Classical Approach Step 4: Use Table VI to determine the critical value using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 115
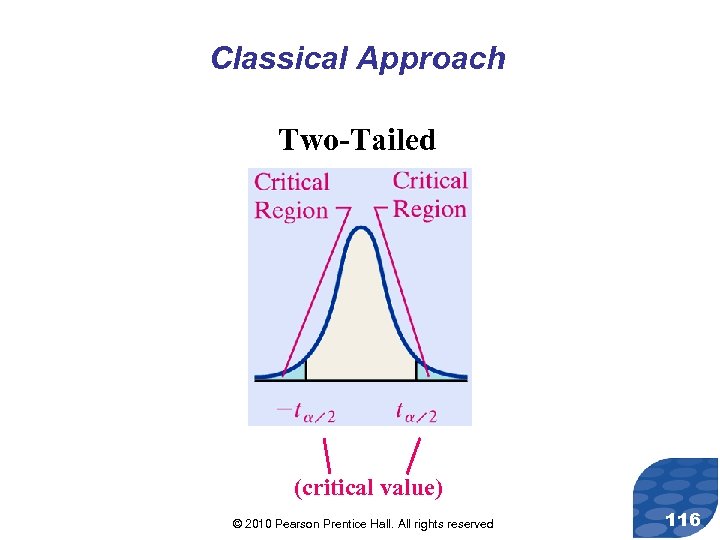 Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 116
Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 116
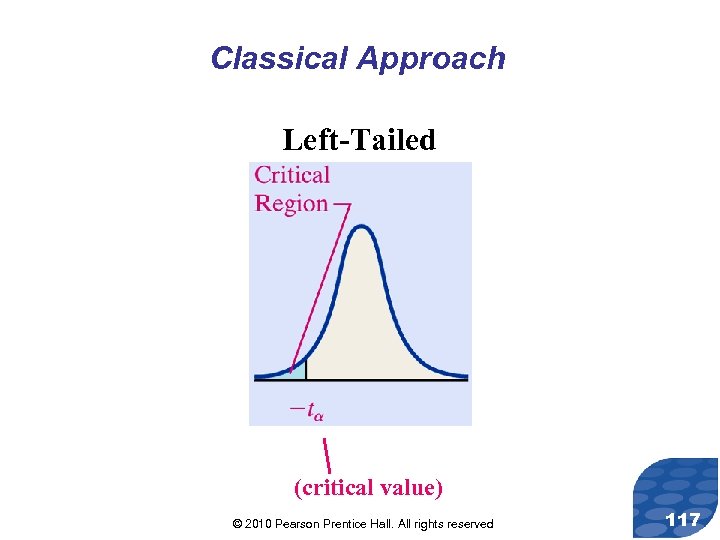 Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 117
Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 117
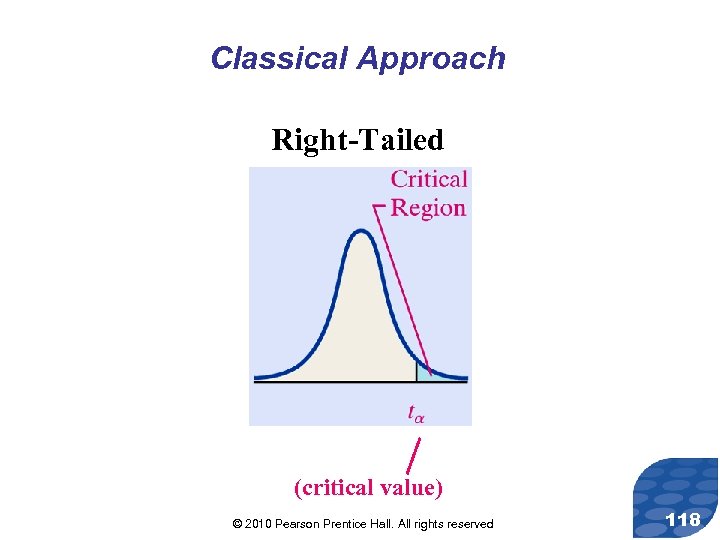 Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 118
Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 118
 Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 119
Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 119
 P-Value Approach Step 4: Use Table VI to determine the P-value using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 120
P-Value Approach Step 4: Use Table VI to determine the P-value using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 120
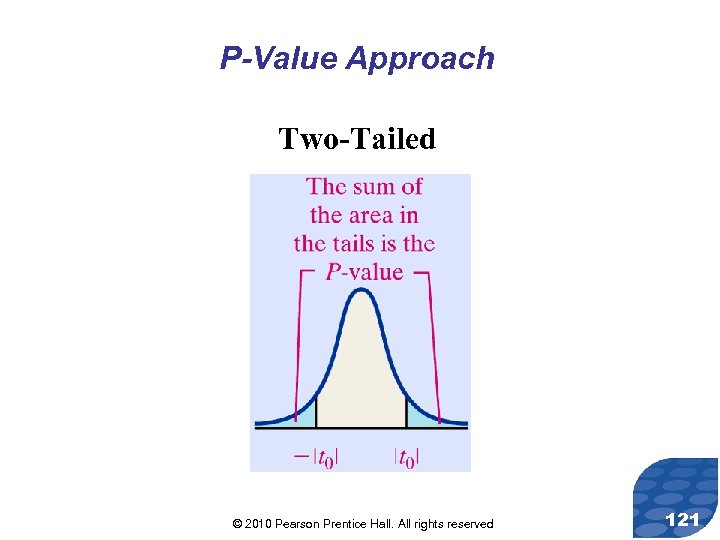 P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 121
P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 121
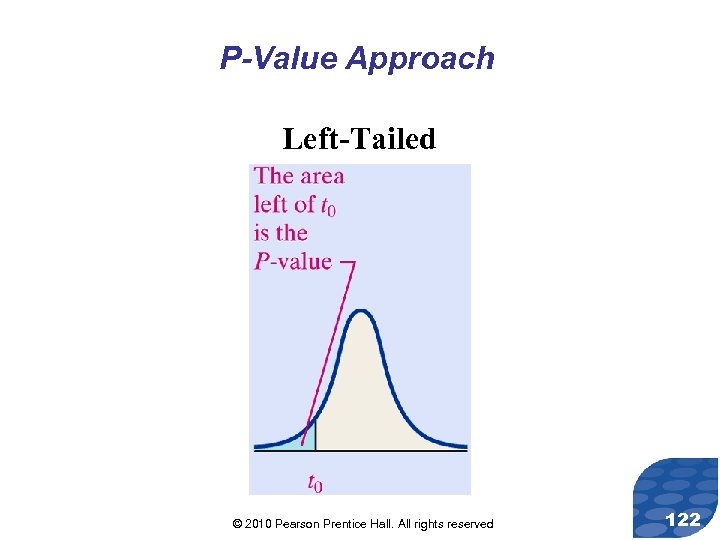 P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 122
P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 122
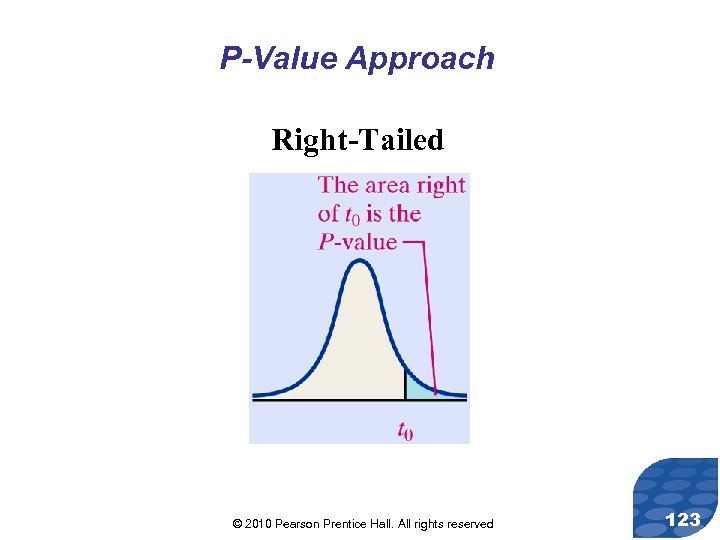 P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 123
P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 123
 P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 124
P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 124
 Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 125
Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 125
 These procedures are robust, which means that minor departures from normality will not adversely affect the results. However, if the data have outliers, the procedure should not be used. © 2010 Pearson Prentice Hall. All rights reserved 126
These procedures are robust, which means that minor departures from normality will not adversely affect the results. However, if the data have outliers, the procedure should not be used. © 2010 Pearson Prentice Hall. All rights reserved 126
 Parallel Example 2: Testing a Claim Regarding Matched-Pairs Data The following data represent the cost of a one night stay in Hampton Inn Hotels and La Quinta Inn Hotels for a random sample of 10 cities. Test the claim that Hampton Inn Hotels are priced differently than La Quinta Hotels at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 127
Parallel Example 2: Testing a Claim Regarding Matched-Pairs Data The following data represent the cost of a one night stay in Hampton Inn Hotels and La Quinta Inn Hotels for a random sample of 10 cities. Test the claim that Hampton Inn Hotels are priced differently than La Quinta Hotels at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 127
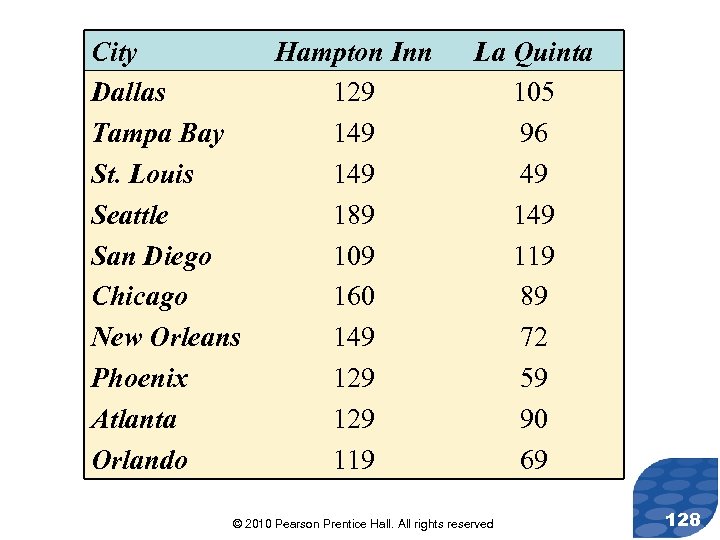 City Dallas Tampa Bay St. Louis Seattle San Diego Chicago New Orleans Phoenix Atlanta Orlando Hampton Inn 129 149 189 109 160 149 129 119 La Quinta 105 96 49 119 89 72 59 90 69 © 2010 Pearson Prentice Hall. All rights reserved 128
City Dallas Tampa Bay St. Louis Seattle San Diego Chicago New Orleans Phoenix Atlanta Orlando Hampton Inn 129 149 189 109 160 149 129 119 La Quinta 105 96 49 119 89 72 59 90 69 © 2010 Pearson Prentice Hall. All rights reserved 128
 Solution This is a matched-pairs design since the hotel prices come from the same ten cities. To test the hypothesis, we first compute the differences and then verify that the differences come from a population that is approximately normally distributed with no outliers because the sample size is small. The differences (Hampton - La Quinta) are: 24 with 53 100 40 -10 71 77 70 39 50 = 51. 4 and sd = 30. 8336. © 2010 Pearson Prentice Hall. All rights reserved 129
Solution This is a matched-pairs design since the hotel prices come from the same ten cities. To test the hypothesis, we first compute the differences and then verify that the differences come from a population that is approximately normally distributed with no outliers because the sample size is small. The differences (Hampton - La Quinta) are: 24 with 53 100 40 -10 71 77 70 39 50 = 51. 4 and sd = 30. 8336. © 2010 Pearson Prentice Hall. All rights reserved 129
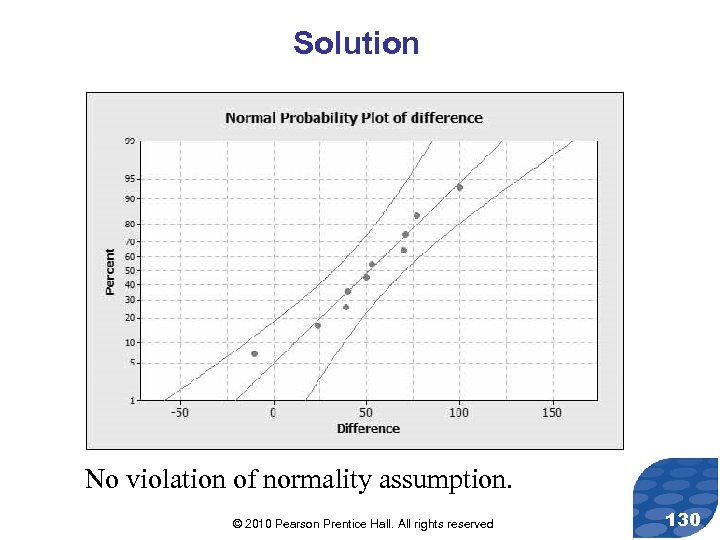 Solution No violation of normality assumption. © 2010 Pearson Prentice Hall. All rights reserved 130
Solution No violation of normality assumption. © 2010 Pearson Prentice Hall. All rights reserved 130
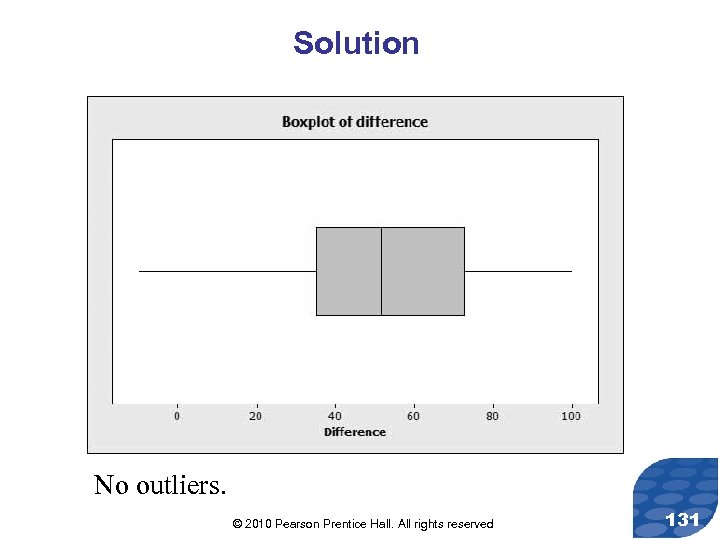 Solution No outliers. © 2010 Pearson Prentice Hall. All rights reserved 131
Solution No outliers. © 2010 Pearson Prentice Hall. All rights reserved 131
 Solution Step 1: We want to determine if the prices differ: H 0: d = 0 versus H 1: d 0 Step 2: The level of significance is =0. 05. Step 3: The test statistic is © 2010 Pearson Prentice Hall. All rights reserved 132
Solution Step 1: We want to determine if the prices differ: H 0: d = 0 versus H 1: d 0 Step 2: The level of significance is =0. 05. Step 3: The test statistic is © 2010 Pearson Prentice Hall. All rights reserved 132
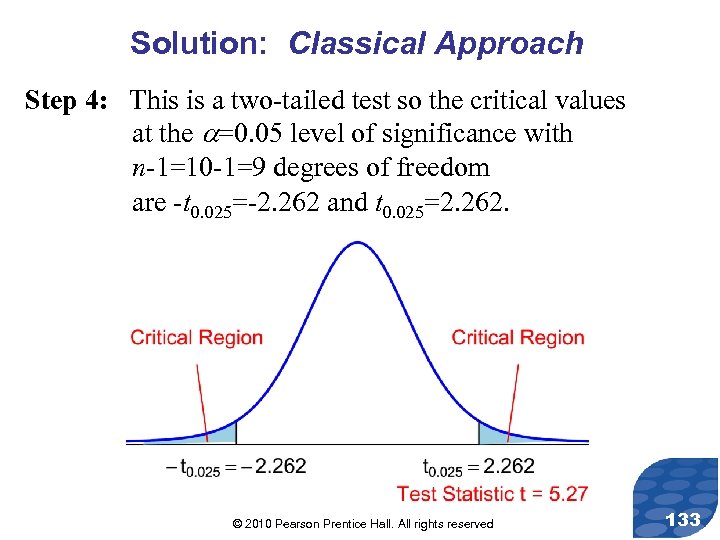 Solution: Classical Approach Step 4: This is a two-tailed test so the critical values at the =0. 05 level of significance with n-1=10 -1=9 degrees of freedom are -t 0. 025=-2. 262 and t 0. 025=2. 262. © 2010 Pearson Prentice Hall. All rights reserved 133
Solution: Classical Approach Step 4: This is a two-tailed test so the critical values at the =0. 05 level of significance with n-1=10 -1=9 degrees of freedom are -t 0. 025=-2. 262 and t 0. 025=2. 262. © 2010 Pearson Prentice Hall. All rights reserved 133
 Solution: Classical Approach Step 5: Since the test statistic, t 0=5. 27 is greater than the critical value t. 025=2. 262, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 134
Solution: Classical Approach Step 5: Since the test statistic, t 0=5. 27 is greater than the critical value t. 025=2. 262, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 134
 Solution: P-Value Approach Step 4: Because this is a two-tailed test, the P-value is two times the area under the t-distribution with n-1=10 -1=9 degrees of freedom to the right of the test statistic t 0=5. 27. That is, P-value = 2 P(t > 5. 27) ≈ 2(0. 00026)=0. 00052 (using technology). Approximately 5 samples in 10, 000 will yield results as extreme as we obtained if the null hypothesis is true. © 2010 Pearson Prentice Hall. All rights reserved 135
Solution: P-Value Approach Step 4: Because this is a two-tailed test, the P-value is two times the area under the t-distribution with n-1=10 -1=9 degrees of freedom to the right of the test statistic t 0=5. 27. That is, P-value = 2 P(t > 5. 27) ≈ 2(0. 00026)=0. 00052 (using technology). Approximately 5 samples in 10, 000 will yield results as extreme as we obtained if the null hypothesis is true. © 2010 Pearson Prentice Hall. All rights reserved 135
 Solution: P-Value Approach Step 5: Since the P-value is less than the level of significance =0. 05, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 136
Solution: P-Value Approach Step 5: Since the P-value is less than the level of significance =0. 05, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 136
 Solution Step 6: There is sufficient evidence to conclude that Hampton Inn hotels and La Quinta hotels are priced differently at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 137
Solution Step 6: There is sufficient evidence to conclude that Hampton Inn hotels and La Quinta hotels are priced differently at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 137
 Objective 3 • Construct and Interpret Confidence Intervals for the Population Mean Difference of Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 138
Objective 3 • Construct and Interpret Confidence Intervals for the Population Mean Difference of Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 138
 Confidence Interval for Matched-Pairs Data A (1 - ) 100% confidence interval for d is given by Lower bound: Upper bound: The critical value t /2 is determined using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 139
Confidence Interval for Matched-Pairs Data A (1 - ) 100% confidence interval for d is given by Lower bound: Upper bound: The critical value t /2 is determined using n-1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 139
 Confidence Interval for Matched-Pairs Data Note: The interval is exact when the population is normally distributed and approximately correct for nonnormal populations, provided that n is large. © 2010 Pearson Prentice Hall. All rights reserved 140
Confidence Interval for Matched-Pairs Data Note: The interval is exact when the population is normally distributed and approximately correct for nonnormal populations, provided that n is large. © 2010 Pearson Prentice Hall. All rights reserved 140
 Parallel Example 4: Constructing a Confidence Interval for Matched-Pairs Data Construct a 90% confidence interval for the mean difference in price of Hampton Inn versus La Quinta hotel rooms. © 2010 Pearson Prentice Hall. All rights reserved 141
Parallel Example 4: Constructing a Confidence Interval for Matched-Pairs Data Construct a 90% confidence interval for the mean difference in price of Hampton Inn versus La Quinta hotel rooms. © 2010 Pearson Prentice Hall. All rights reserved 141
 Solution • We have already verified that the differenced data come from a population that is approximately normal with no outliers. • Recall • From Table VI with = 0. 10 and 9 degrees of freedom, we find t /2 = 1. 833. = 51. 4 and sd = 30. 8336. © 2010 Pearson Prentice Hall. All rights reserved 142
Solution • We have already verified that the differenced data come from a population that is approximately normal with no outliers. • Recall • From Table VI with = 0. 10 and 9 degrees of freedom, we find t /2 = 1. 833. = 51. 4 and sd = 30. 8336. © 2010 Pearson Prentice Hall. All rights reserved 142
 Solution Thus, • Lower bound = • Upper bound = We are 90% confident that the mean difference in hotel room price for Ramada Inn versus La Quinta Inn is between $33. 53 and $69. 27. © 2010 Pearson Prentice Hall. All rights reserved 143
Solution Thus, • Lower bound = • Upper bound = We are 90% confident that the mean difference in hotel room price for Ramada Inn versus La Quinta Inn is between $33. 53 and $69. 27. © 2010 Pearson Prentice Hall. All rights reserved 143
 Section 11. 2 Inference about Two Means: Independent Samples © 2010 Pearson Prentice Hall. All rights reserved
Section 11. 2 Inference about Two Means: Independent Samples © 2010 Pearson Prentice Hall. All rights reserved
 Objectives 1. Test hypotheses regarding the difference of two independent means 2. Construct and interpret confidence intervals regarding the difference of two independent means © 2010 Pearson Prentice Hall. All rights reserved 145
Objectives 1. Test hypotheses regarding the difference of two independent means 2. Construct and interpret confidence intervals regarding the difference of two independent means © 2010 Pearson Prentice Hall. All rights reserved 145
 Sampling Distribution of the Difference of Two Means: Independent Samples with Population Standard Deviations Unknown (Welch’s t) Suppose that a simple random sample of size n 1 is taken from a population with unknown mean 1 and unknown standard deviation 1. In addition, a simple random sample of size n 2 is taken from a population with unknown mean 2 and unknown standard deviation 2. If the two populations are normally distributed or the sample sizes are sufficiently large (n 1 ≥ 30, n 2 ≥ 30) , then approximately follows Student’s t-distribution with the smaller of n 1 -1 or n 2 -1 degrees of freedom where is the sample mean and si is the sample standard deviation from population i. © 2010 Pearson Prentice Hall. All rights reserved 146
Sampling Distribution of the Difference of Two Means: Independent Samples with Population Standard Deviations Unknown (Welch’s t) Suppose that a simple random sample of size n 1 is taken from a population with unknown mean 1 and unknown standard deviation 1. In addition, a simple random sample of size n 2 is taken from a population with unknown mean 2 and unknown standard deviation 2. If the two populations are normally distributed or the sample sizes are sufficiently large (n 1 ≥ 30, n 2 ≥ 30) , then approximately follows Student’s t-distribution with the smaller of n 1 -1 or n 2 -1 degrees of freedom where is the sample mean and si is the sample standard deviation from population i. © 2010 Pearson Prentice Hall. All rights reserved 146
 Objective 1 • Test Hypotheses Regarding the Difference of Two Independent Means © 2010 Pearson Prentice Hall. All rights reserved 147
Objective 1 • Test Hypotheses Regarding the Difference of Two Independent Means © 2010 Pearson Prentice Hall. All rights reserved 147
 Testing Hypotheses Regarding the Difference of Two Means To test hypotheses regarding two population means, 1 and 2, with unknown population standard deviations, we can use the following steps, provided that: 1. the samples are obtained using simple random sampling; 2. the samples are independent; 3. the populations from which the samples are drawn are normally distributed or the sample sizes are large (n 1 ≥ 30, n 2 ≥ 30). © 2010 Pearson Prentice Hall. All rights reserved 148
Testing Hypotheses Regarding the Difference of Two Means To test hypotheses regarding two population means, 1 and 2, with unknown population standard deviations, we can use the following steps, provided that: 1. the samples are obtained using simple random sampling; 2. the samples are independent; 3. the populations from which the samples are drawn are normally distributed or the sample sizes are large (n 1 ≥ 30, n 2 ≥ 30). © 2010 Pearson Prentice Hall. All rights reserved 148
 Step 1: Determine the null and alternative hypotheses. The hypotheses are structured in one of three ways: © 2010 Pearson Prentice Hall. All rights reserved 149
Step 1: Determine the null and alternative hypotheses. The hypotheses are structured in one of three ways: © 2010 Pearson Prentice Hall. All rights reserved 149
 Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 150
Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 150
 Step 3: Compute the test statistic which approximately follows Student’s t - distribution. © 2010 Pearson Prentice Hall. All rights reserved 151
Step 3: Compute the test statistic which approximately follows Student’s t - distribution. © 2010 Pearson Prentice Hall. All rights reserved 151
 Classical Approach Step 4: Use Table VI to determine the critical value using the smaller of n 1 -1 or n 2 -1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 152
Classical Approach Step 4: Use Table VI to determine the critical value using the smaller of n 1 -1 or n 2 -1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 152
 Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 153
Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 153
 Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 154
Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 154
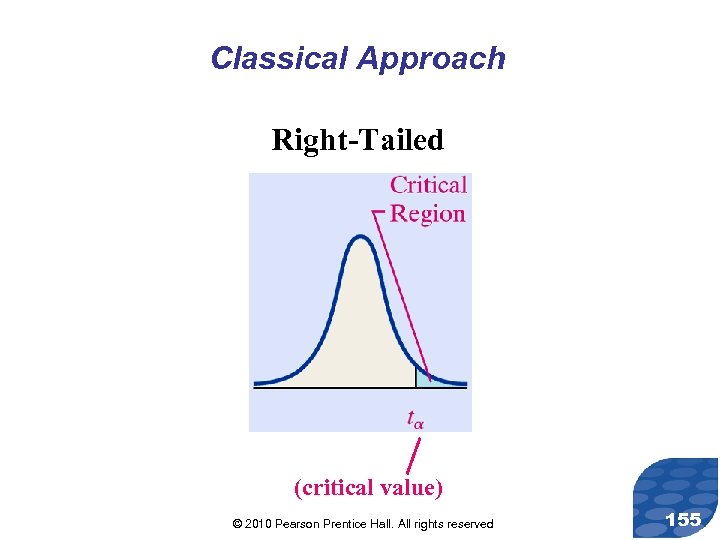 Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 155
Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 155
 Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 156
Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 156
 P-Value Approach Step 4: Use Table VI to determine the P-value using the smaller of n 1 -1 or n 2 -1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 157
P-Value Approach Step 4: Use Table VI to determine the P-value using the smaller of n 1 -1 or n 2 -1 degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 157
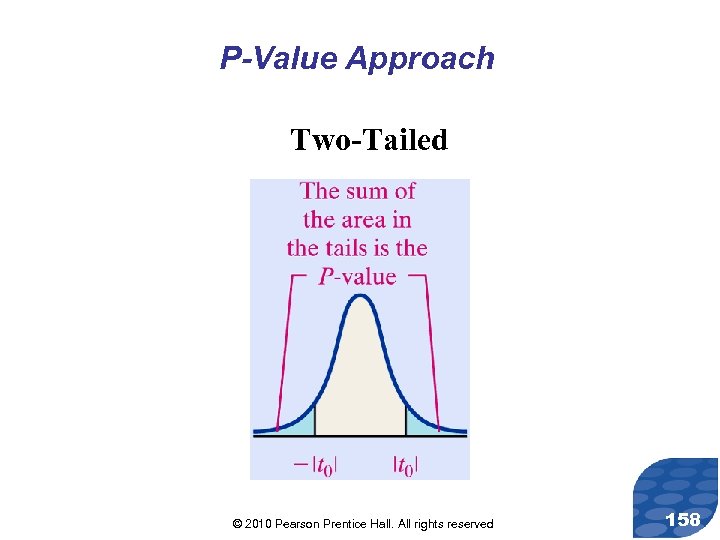 P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 158
P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 158
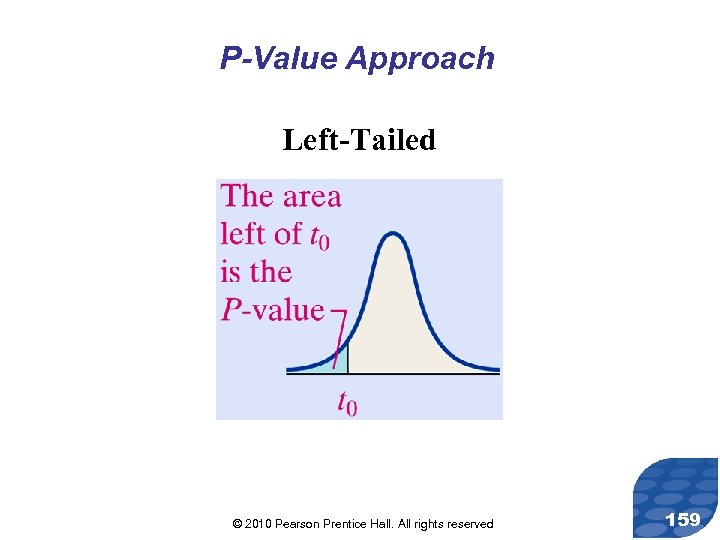 P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 159
P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 159
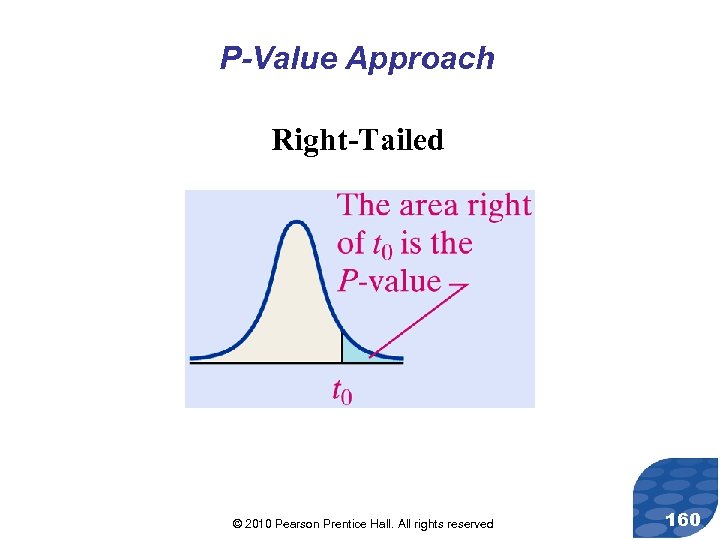 P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 160
P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 160
 P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 161
P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 161
 Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 162
Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 162
 These procedures are robust, which means that minor departures from normality will not adversely affect the results. However, if the data have outliers, the procedure should not be used. © 2010 Pearson Prentice Hall. All rights reserved 163
These procedures are robust, which means that minor departures from normality will not adversely affect the results. However, if the data have outliers, the procedure should not be used. © 2010 Pearson Prentice Hall. All rights reserved 163
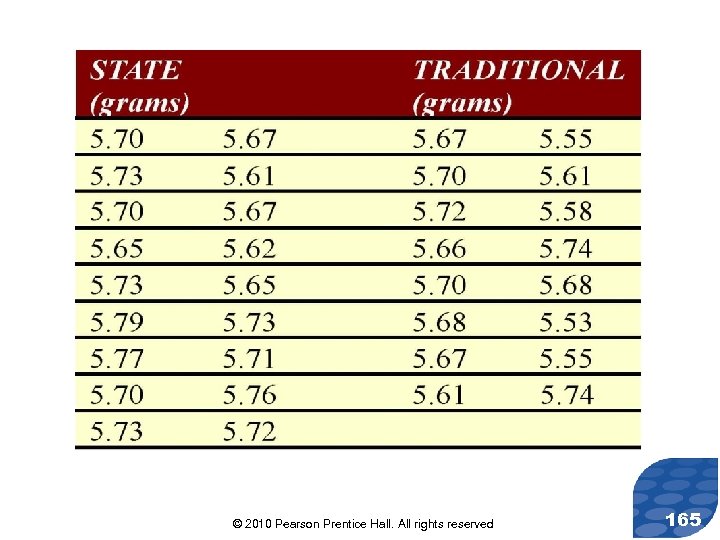
 Parallel Example 1: Testing Hypotheses Regarding Two Means A researcher wanted to know whether “state” quarters had a weight that is more than “traditional” quarters. He randomly selected 18 “state” quarters and 16 “traditional” quarters, weighed each of them and obtained the following data. © 2010 Pearson Prentice Hall. All rights reserved 164
Parallel Example 1: Testing Hypotheses Regarding Two Means A researcher wanted to know whether “state” quarters had a weight that is more than “traditional” quarters. He randomly selected 18 “state” quarters and 16 “traditional” quarters, weighed each of them and obtained the following data. © 2010 Pearson Prentice Hall. All rights reserved 164
 © 2010 Pearson Prentice Hall. All rights reserved 165
© 2010 Pearson Prentice Hall. All rights reserved 165
 Test the claim that “state” quarters have a mean weight that is more than “traditional” quarters at the =0. 05 level of significance. NOTE: A normal probability plot of “state” quarters indicates the population could be normal. A normal probability plot of “traditional” quarters indicates the population could be normal © 2010 Pearson Prentice Hall. All rights reserved 166
Test the claim that “state” quarters have a mean weight that is more than “traditional” quarters at the =0. 05 level of significance. NOTE: A normal probability plot of “state” quarters indicates the population could be normal. A normal probability plot of “traditional” quarters indicates the population could be normal © 2010 Pearson Prentice Hall. All rights reserved 166
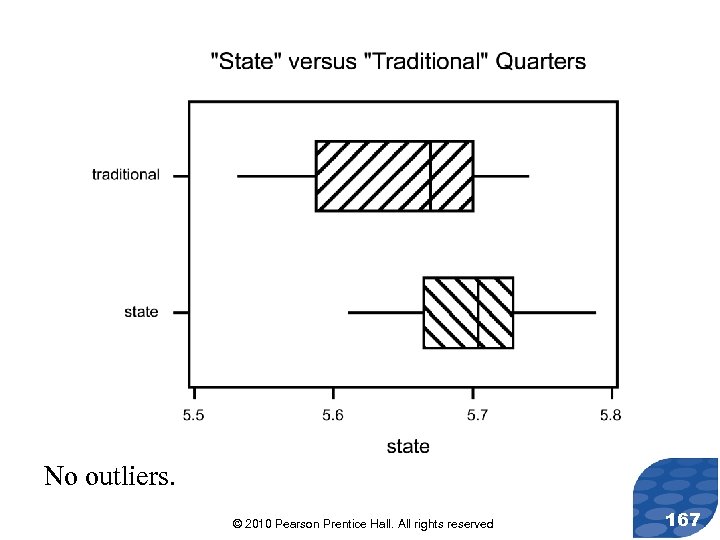 No outliers. © 2010 Pearson Prentice Hall. All rights reserved 167
No outliers. © 2010 Pearson Prentice Hall. All rights reserved 167
 Solution Step 1: We want to determine whether state quarters weigh more than traditional quarters: H 0: 1 = 2 versus H 1: 1 > 2 Step 2: The level of significance is =0. 05. Step 3: The test statistic is © 2010 Pearson Prentice Hall. All rights reserved 168
Solution Step 1: We want to determine whether state quarters weigh more than traditional quarters: H 0: 1 = 2 versus H 1: 1 > 2 Step 2: The level of significance is =0. 05. Step 3: The test statistic is © 2010 Pearson Prentice Hall. All rights reserved 168
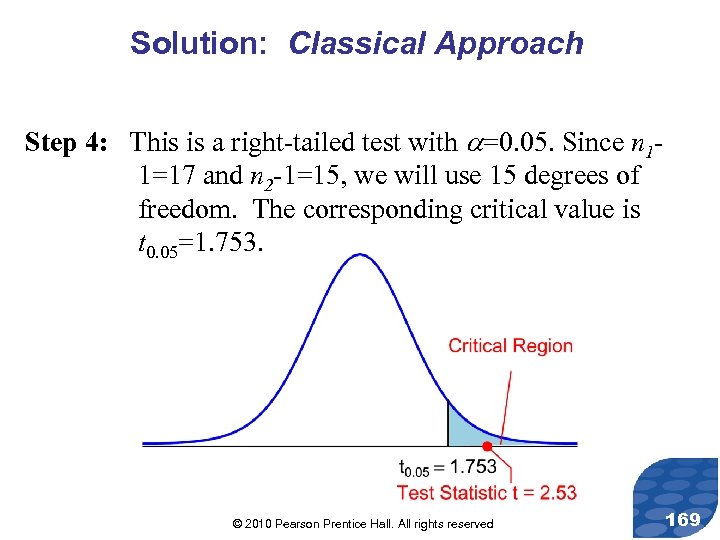 Solution: Classical Approach Step 4: This is a right-tailed test with =0. 05. Since n 11=17 and n 2 -1=15, we will use 15 degrees of freedom. The corresponding critical value is t 0. 05=1. 753. © 2010 Pearson Prentice Hall. All rights reserved 169
Solution: Classical Approach Step 4: This is a right-tailed test with =0. 05. Since n 11=17 and n 2 -1=15, we will use 15 degrees of freedom. The corresponding critical value is t 0. 05=1. 753. © 2010 Pearson Prentice Hall. All rights reserved 169
 Solution: Classical Approach Step 5: Since the test statistic, t 0=2. 53 is greater than the critical value t. 05=1. 753, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 170
Solution: Classical Approach Step 5: Since the test statistic, t 0=2. 53 is greater than the critical value t. 05=1. 753, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 170
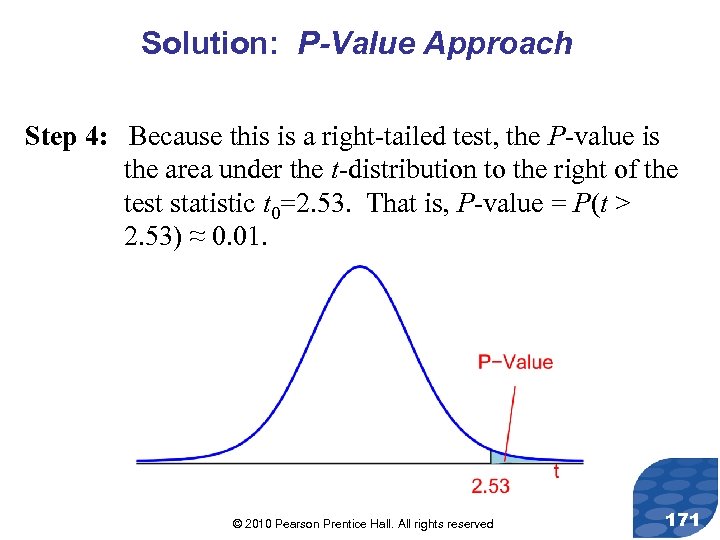 Solution: P-Value Approach Step 4: Because this is a right-tailed test, the P-value is the area under the t-distribution to the right of the test statistic t 0=2. 53. That is, P-value = P(t > 2. 53) ≈ 0. 01. © 2010 Pearson Prentice Hall. All rights reserved 171
Solution: P-Value Approach Step 4: Because this is a right-tailed test, the P-value is the area under the t-distribution to the right of the test statistic t 0=2. 53. That is, P-value = P(t > 2. 53) ≈ 0. 01. © 2010 Pearson Prentice Hall. All rights reserved 171
 Solution: P-Value Approach Step 5: Since the P-value is less than the level of significance =0. 05, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 172
Solution: P-Value Approach Step 5: Since the P-value is less than the level of significance =0. 05, we reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 172
 Solution Step 6: There is sufficient evidence at the =0. 05 level to conclude that the state quarters weigh more than the traditional quarters. © 2010 Pearson Prentice Hall. All rights reserved 173
Solution Step 6: There is sufficient evidence at the =0. 05 level to conclude that the state quarters weigh more than the traditional quarters. © 2010 Pearson Prentice Hall. All rights reserved 173
 NOTE: The degrees of freedom used to determine the critical value in the last example are conservative. Results that are more accurate can be obtained by using the following degrees of freedom: © 2010 Pearson Prentice Hall. All rights reserved 174
NOTE: The degrees of freedom used to determine the critical value in the last example are conservative. Results that are more accurate can be obtained by using the following degrees of freedom: © 2010 Pearson Prentice Hall. All rights reserved 174
 Objective 3 • Construct and Interpret Confidence Intervals Regarding the Difference of Two Independent Means © 2010 Pearson Prentice Hall. All rights reserved 175
Objective 3 • Construct and Interpret Confidence Intervals Regarding the Difference of Two Independent Means © 2010 Pearson Prentice Hall. All rights reserved 175
 Constructing a (1 - ) 100% Confidence Interval for the Difference of Two Means A simple random sample of size n 1 is taken from a population with unknown mean 1 and unknown standard deviation 1. Also, a simple random sample of size n 2 is taken from a population with unknown mean 2 and unknown standard deviation 2. If the two populations are normally distributed or the sample sizes are sufficiently large (n 1≥ 30 and n 2≥ 30), a (1 - ) 100% confidence interval about 1 - 2 is given by Lower bound: Upper bound: © 2010 Pearson Prentice Hall. All rights reserved 176
Constructing a (1 - ) 100% Confidence Interval for the Difference of Two Means A simple random sample of size n 1 is taken from a population with unknown mean 1 and unknown standard deviation 1. Also, a simple random sample of size n 2 is taken from a population with unknown mean 2 and unknown standard deviation 2. If the two populations are normally distributed or the sample sizes are sufficiently large (n 1≥ 30 and n 2≥ 30), a (1 - ) 100% confidence interval about 1 - 2 is given by Lower bound: Upper bound: © 2010 Pearson Prentice Hall. All rights reserved 176
 Parallel Example 3: Constructing a Confidence Interval for the Difference of Two Means Construct a 95% confidence interval about the difference between the population mean weight of a “state” quarter versus the population mean weight of a “traditional” quarter. © 2010 Pearson Prentice Hall. All rights reserved 177
Parallel Example 3: Constructing a Confidence Interval for the Difference of Two Means Construct a 95% confidence interval about the difference between the population mean weight of a “state” quarter versus the population mean weight of a “traditional” quarter. © 2010 Pearson Prentice Hall. All rights reserved 177
 Solution • We have already verified that the populations are approximately normal and that there are no outliers. • Recall = 5. 702, s 1 = 0. 0497, 0. 0689. • From Table VI with = 0. 05 and 15 degrees of freedom, we find t /2 = 2. 131. =5. 6494 and s 2 = © 2010 Pearson Prentice Hall. All rights reserved 178
Solution • We have already verified that the populations are approximately normal and that there are no outliers. • Recall = 5. 702, s 1 = 0. 0497, 0. 0689. • From Table VI with = 0. 05 and 15 degrees of freedom, we find t /2 = 2. 131. =5. 6494 and s 2 = © 2010 Pearson Prentice Hall. All rights reserved 178
 Solution Thus, • Lower bound = • Upper bound = © 2010 Pearson Prentice Hall. All rights reserved 179
Solution Thus, • Lower bound = • Upper bound = © 2010 Pearson Prentice Hall. All rights reserved 179
 Solution We are 95% confident that the mean weight of the “state” quarters is between 0. 0086 and 0. 0974 ounces more than the mean weight of the “traditional” quarters. Since the confidence interval does not contain 0, we conclude that the “state” quarters weigh more than the “traditional” quarters. © 2010 Pearson Prentice Hall. All rights reserved 180
Solution We are 95% confident that the mean weight of the “state” quarters is between 0. 0086 and 0. 0974 ounces more than the mean weight of the “traditional” quarters. Since the confidence interval does not contain 0, we conclude that the “state” quarters weigh more than the “traditional” quarters. © 2010 Pearson Prentice Hall. All rights reserved 180
 When the population variances are assumed to be equal, the pooled t-statistic can be used to test for a difference in means for two independent samples. The pooled t-statistic is computed by finding a weighted average of the sample variances and using this average in the computation of the test statistic. • The advantage to this test statistic is that it exactly follows Student’s t-distribution with n 1+n 2 -2 degrees of freedom. • The disadvantage to this test statistic is that it requires that the population variances be equal. © 2010 Pearson Prentice Hall. All rights reserved 181
When the population variances are assumed to be equal, the pooled t-statistic can be used to test for a difference in means for two independent samples. The pooled t-statistic is computed by finding a weighted average of the sample variances and using this average in the computation of the test statistic. • The advantage to this test statistic is that it exactly follows Student’s t-distribution with n 1+n 2 -2 degrees of freedom. • The disadvantage to this test statistic is that it requires that the population variances be equal. © 2010 Pearson Prentice Hall. All rights reserved 181
 Section 11. 3 Inference about Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved
Section 11. 3 Inference about Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved
 Objectives 1. Test hypotheses regarding two population proportions 2. Construct and interpret confidence intervals for the difference between two population proportions 3. Use Mc. Nemar’s Test to compare two proportions from matched-pairs data 4. Determine the sample size necessary for estimating the difference between two population proportions within a specified margin of error. © 2010 Pearson Prentice Hall. All rights reserved 183
Objectives 1. Test hypotheses regarding two population proportions 2. Construct and interpret confidence intervals for the difference between two population proportions 3. Use Mc. Nemar’s Test to compare two proportions from matched-pairs data 4. Determine the sample size necessary for estimating the difference between two population proportions within a specified margin of error. © 2010 Pearson Prentice Hall. All rights reserved 183
 Sampling Distribution of the Difference between Two Proportions Suppose that a simple random sample of size n 1 is taken from a population where x 1 of the individuals have a specified characteristic, and a simple random sample of size n 2 is independently taken from a different population where x 2 of the individuals have a specified characteristic. The sampling distribution of , where and , is approximately normal, with mean and standard deviation provided that and © 2010 Pearson Prentice Hall. All rights reserved . 184
Sampling Distribution of the Difference between Two Proportions Suppose that a simple random sample of size n 1 is taken from a population where x 1 of the individuals have a specified characteristic, and a simple random sample of size n 2 is independently taken from a different population where x 2 of the individuals have a specified characteristic. The sampling distribution of , where and , is approximately normal, with mean and standard deviation provided that and © 2010 Pearson Prentice Hall. All rights reserved . 184
 Sampling Distribution of the Difference between Two Proportions The standardized version of is then written as which has an approximate standard normal distribution. © 2010 Pearson Prentice Hall. All rights reserved 185
Sampling Distribution of the Difference between Two Proportions The standardized version of is then written as which has an approximate standard normal distribution. © 2010 Pearson Prentice Hall. All rights reserved 185
 Objective 1 • Test Hypotheses Regarding Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 186
Objective 1 • Test Hypotheses Regarding Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 186
 The best point estimate of p is called the pooled estimate of p, denoted , where Test statistic for Comparing Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 187
The best point estimate of p is called the pooled estimate of p, denoted , where Test statistic for Comparing Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 187
 Hypothesis Test Regarding the Difference between Two Population Proportions To test hypotheses regarding two population proportions, p 1 and p 2, we can use the steps that follow, provided that: 1. the samples are independently obtained using simple random sampling, 2. and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. © 2010 Pearson Prentice Hall. All rights reserved 188
Hypothesis Test Regarding the Difference between Two Population Proportions To test hypotheses regarding two population proportions, p 1 and p 2, we can use the steps that follow, provided that: 1. the samples are independently obtained using simple random sampling, 2. and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. © 2010 Pearson Prentice Hall. All rights reserved 188
 Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways: © 2010 Pearson Prentice Hall. All rights reserved 189
Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways: © 2010 Pearson Prentice Hall. All rights reserved 189
 Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 190
Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 190
 Step 3: Compute the test statistic where © 2010 Pearson Prentice Hall. All rights reserved 191
Step 3: Compute the test statistic where © 2010 Pearson Prentice Hall. All rights reserved 191
 Classical Approach Step 4: Use Table V to determine the critical value. © 2010 Pearson Prentice Hall. All rights reserved 192
Classical Approach Step 4: Use Table V to determine the critical value. © 2010 Pearson Prentice Hall. All rights reserved 192
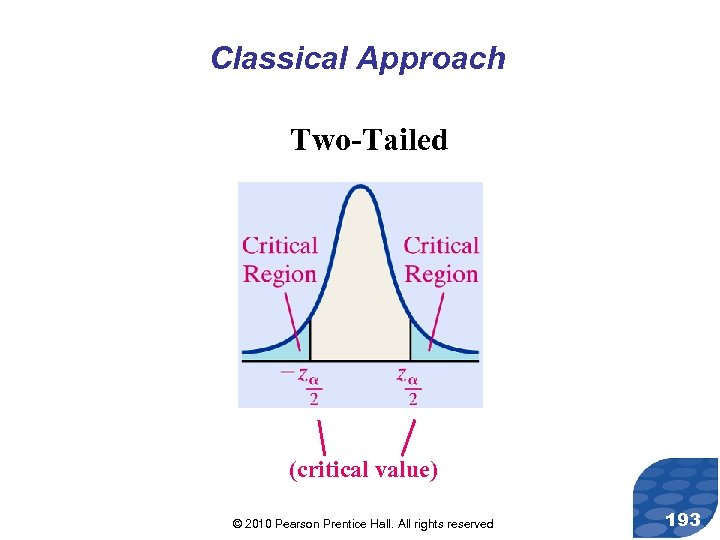 Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 193
Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 193
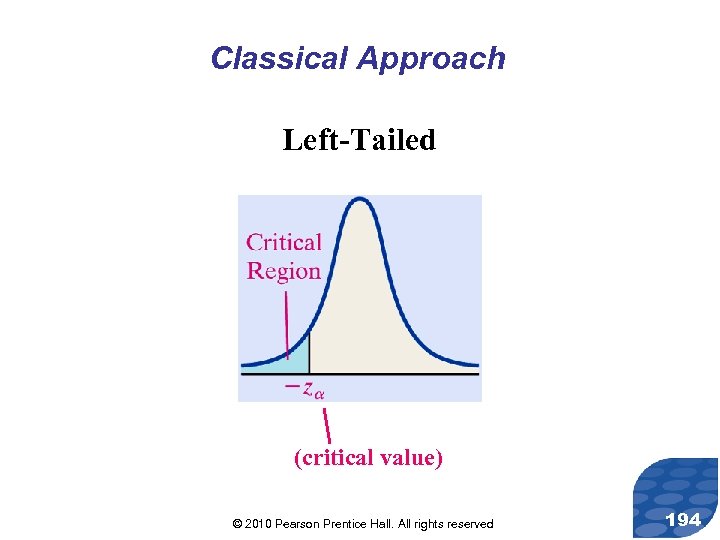 Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 194
Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 194
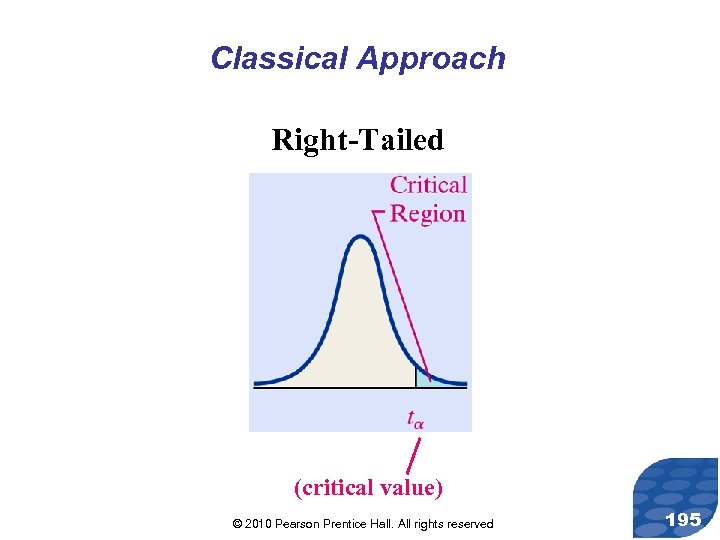 Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 195
Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 195
 Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 196
Classical Approach Step 5: Compare the critical value with the test statistic: © 2010 Pearson Prentice Hall. All rights reserved 196
 P-Value Approach Step 4: Use Table V to estimate the P-value. . © 2010 Pearson Prentice Hall. All rights reserved 197
P-Value Approach Step 4: Use Table V to estimate the P-value. . © 2010 Pearson Prentice Hall. All rights reserved 197
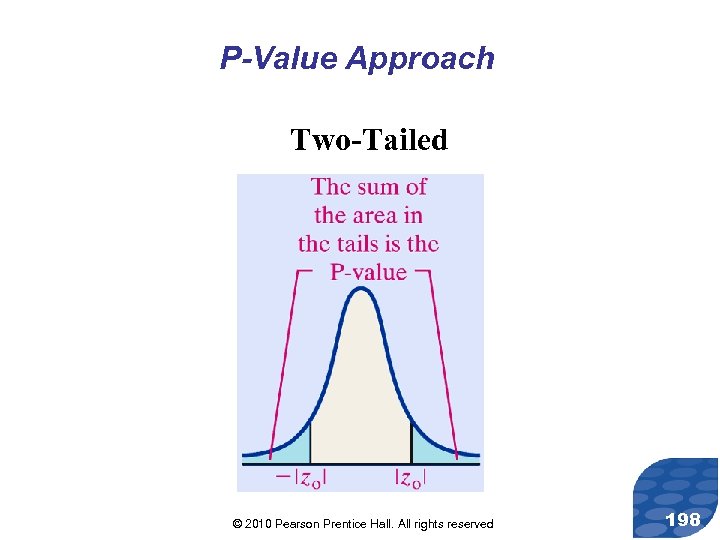 P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 198
P-Value Approach Two-Tailed © 2010 Pearson Prentice Hall. All rights reserved 198
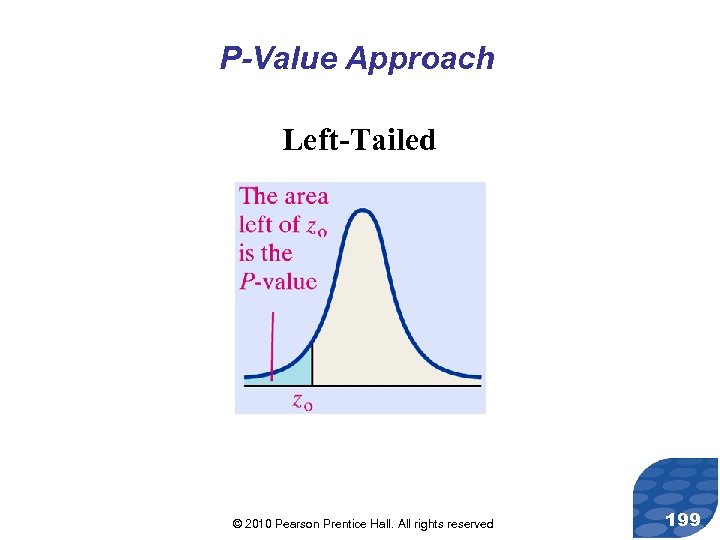 P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 199
P-Value Approach Left-Tailed © 2010 Pearson Prentice Hall. All rights reserved 199
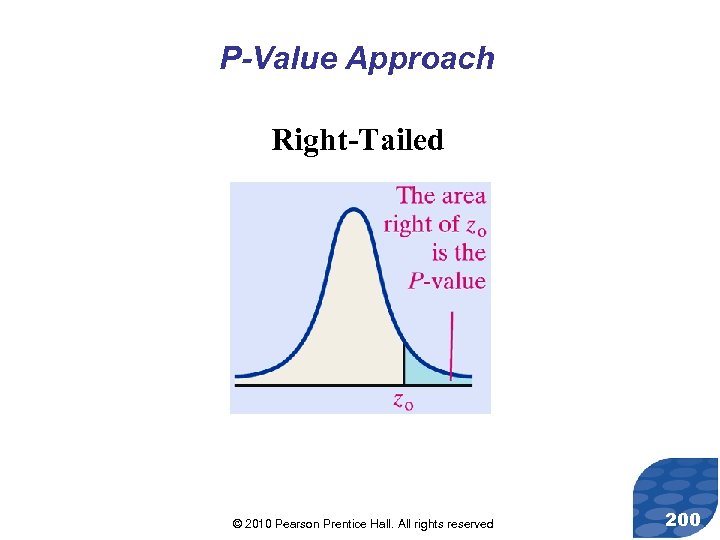 P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 200
P-Value Approach Right-Tailed © 2010 Pearson Prentice Hall. All rights reserved 200
 P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 201
P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 201
 Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 202
Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 202
 Parallel Example 1: Testing Hypotheses Regarding Two Population Proportions An economist believes that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. He obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Test the economist’s claim at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 203
Parallel Example 1: Testing Hypotheses Regarding Two Population Proportions An economist believes that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. He obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Test the economist’s claim at the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 203
 Solution We must first verify that the requirements are satisfied: 1. The samples are simple random samples that were obtained independently. 2. x 1=338, n 1=800, x 2=292 and n 2=750, so 3. The sample sizes are less than 5% of the population size. © 2010 Pearson Prentice Hall. All rights reserved 204
Solution We must first verify that the requirements are satisfied: 1. The samples are simple random samples that were obtained independently. 2. x 1=338, n 1=800, x 2=292 and n 2=750, so 3. The sample sizes are less than 5% of the population size. © 2010 Pearson Prentice Hall. All rights reserved 204
 Solution Step 1: We want to determine whether the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. So, H 0: p 1 = p 2 versus H 1: p 1 > p 2 versus H 1: p 1 - p 2 > 0 or, equivalently, H 0: p 1 - p 2=0 Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 205
Solution Step 1: We want to determine whether the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. So, H 0: p 1 = p 2 versus H 1: p 1 > p 2 versus H 1: p 1 - p 2 > 0 or, equivalently, H 0: p 1 - p 2=0 Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 205
 Solution Step 3: The pooled estimate of is: The test statistic is: © 2010 Pearson Prentice Hall. All rights reserved 206
Solution Step 3: The pooled estimate of is: The test statistic is: © 2010 Pearson Prentice Hall. All rights reserved 206
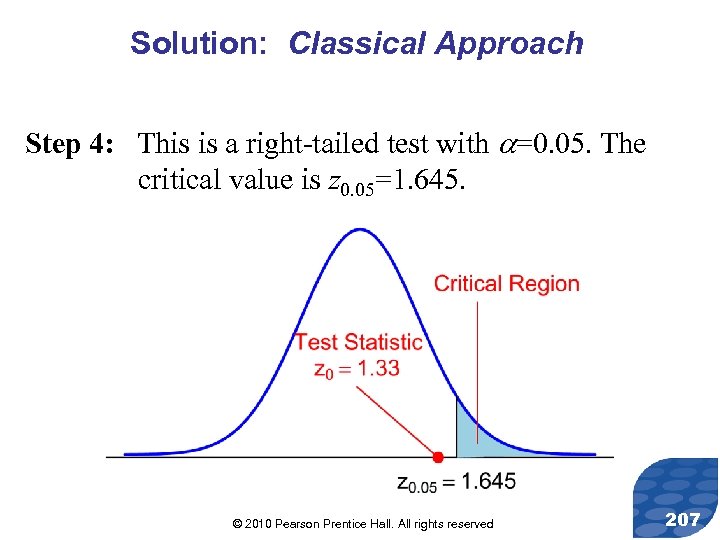 Solution: Classical Approach Step 4: This is a right-tailed test with =0. 05. The critical value is z 0. 05=1. 645. © 2010 Pearson Prentice Hall. All rights reserved 207
Solution: Classical Approach Step 4: This is a right-tailed test with =0. 05. The critical value is z 0. 05=1. 645. © 2010 Pearson Prentice Hall. All rights reserved 207
 Solution: Classical Approach Step 5: Since the test statistic, z 0=1. 33 is less than the critical value z. 05=1. 645, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 208
Solution: Classical Approach Step 5: Since the test statistic, z 0=1. 33 is less than the critical value z. 05=1. 645, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 208
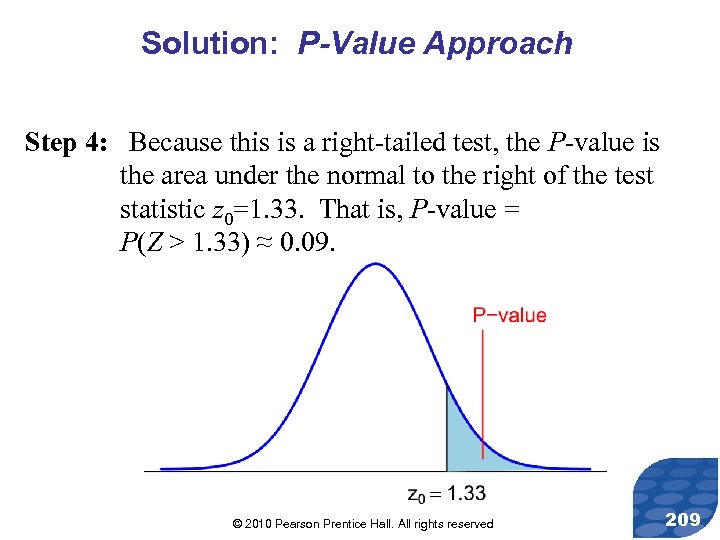 Solution: P-Value Approach Step 4: Because this is a right-tailed test, the P-value is the area under the normal to the right of the test statistic z 0=1. 33. That is, P-value = P(Z > 1. 33) ≈ 0. 09. © 2010 Pearson Prentice Hall. All rights reserved 209
Solution: P-Value Approach Step 4: Because this is a right-tailed test, the P-value is the area under the normal to the right of the test statistic z 0=1. 33. That is, P-value = P(Z > 1. 33) ≈ 0. 09. © 2010 Pearson Prentice Hall. All rights reserved 209
 Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance =0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 210
Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance =0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 210
 Solution Step 6: There is insufficient evidence at the =0. 05 level to conclude that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. © 2010 Pearson Prentice Hall. All rights reserved 211
Solution Step 6: There is insufficient evidence at the =0. 05 level to conclude that the percentage of urban households with Internet access is greater than the percentage of rural households with Internet access. © 2010 Pearson Prentice Hall. All rights reserved 211
 Objective 2 • Construct and Interpret Confidence Intervals for the Difference between Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 212
Objective 2 • Construct and Interpret Confidence Intervals for the Difference between Two Population Proportions © 2010 Pearson Prentice Hall. All rights reserved 212
 Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions To construct a (1 - ) 100% confidence interval for the difference between two population proportions, the following requirements must be satisfied: 1. the samples are obtained independently using simple random sampling, 2. , and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. © 2010 Pearson Prentice Hall. All rights reserved 213
Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions To construct a (1 - ) 100% confidence interval for the difference between two population proportions, the following requirements must be satisfied: 1. the samples are obtained independently using simple random sampling, 2. , and 3. n 1 ≤ 0. 05 N 1 and n 2 ≤ 0. 05 N 2 (the sample size is no more than 5% of the population size); this requirement ensures the independence necessary for a binomial experiment. © 2010 Pearson Prentice Hall. All rights reserved 213
 Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions Provided that these requirements are met, a (1 - ) 100% confidence interval for p 1 -p 2 is given by Lower bound: Upper bound: © 2010 Pearson Prentice Hall. All rights reserved 214
Constructing a (1 - ) 100% Confidence Interval for the Difference between Two Population Proportions Provided that these requirements are met, a (1 - ) 100% confidence interval for p 1 -p 2 is given by Lower bound: Upper bound: © 2010 Pearson Prentice Hall. All rights reserved 214
 Parallel Example 3: Constructing a Confidence Interval for the Difference between Two Population Proportions An economist obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Find a 99% confidence interval for the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access. © 2010 Pearson Prentice Hall. All rights reserved 215
Parallel Example 3: Constructing a Confidence Interval for the Difference between Two Population Proportions An economist obtains a random sample of 800 urban households and finds that 338 of them have Internet access. He obtains a random sample of 750 rural households and finds that 292 of them have Internet access. Find a 99% confidence interval for the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access. © 2010 Pearson Prentice Hall. All rights reserved 215
 Solution We have already verified the requirements for constructing a confidence interval for the difference between two population proportions in the previous example. Recall © 2010 Pearson Prentice Hall. All rights reserved 216
Solution We have already verified the requirements for constructing a confidence interval for the difference between two population proportions in the previous example. Recall © 2010 Pearson Prentice Hall. All rights reserved 216
 Solution Thus, Lower bound = Upper bound = © 2010 Pearson Prentice Hall. All rights reserved 217
Solution Thus, Lower bound = Upper bound = © 2010 Pearson Prentice Hall. All rights reserved 217
 Solution We are 99% confident that the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access is between -0. 03 and 0. 10. Since the confidence interval contains 0, we are unable to conclude that the proportion of urban households with Internet access is greater than the proportion of rural households with Internet access. © 2010 Pearson Prentice Hall. All rights reserved 218
Solution We are 99% confident that the difference between the proportion of urban households that have Internet access and the proportion of rural households that have Internet access is between -0. 03 and 0. 10. Since the confidence interval contains 0, we are unable to conclude that the proportion of urban households with Internet access is greater than the proportion of rural households with Internet access. © 2010 Pearson Prentice Hall. All rights reserved 218
 Objective 3 • Use Mc. Nemar’s Test to Compare Two Proportions from Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 219
Objective 3 • Use Mc. Nemar’s Test to Compare Two Proportions from Matched-Pairs Data © 2010 Pearson Prentice Hall. All rights reserved 219
 Mc. Nemar’s Test is a test that can be used to compare two proportions with matched-pairs data (i. e. , dependent samples) © 2010 Pearson Prentice Hall. All rights reserved 220
Mc. Nemar’s Test is a test that can be used to compare two proportions with matched-pairs data (i. e. , dependent samples) © 2010 Pearson Prentice Hall. All rights reserved 220
 Testing a Hypothesis Regarding the Difference of Two Population Proportions: Dependent Samples To test hypotheses regarding two population proportions p 1 and p 2, where the samples are dependent, arrange the data in a contingency table as follows: Treatment A Success Failure Treatment B Success f 11 f 12 Failure f 21 f 22 © 2010 Pearson Prentice Hall. All rights reserved 221
Testing a Hypothesis Regarding the Difference of Two Population Proportions: Dependent Samples To test hypotheses regarding two population proportions p 1 and p 2, where the samples are dependent, arrange the data in a contingency table as follows: Treatment A Success Failure Treatment B Success f 11 f 12 Failure f 21 f 22 © 2010 Pearson Prentice Hall. All rights reserved 221
 Testing a Hypothesis Regarding the Difference of Two Population Proportions: Dependent Samples We can use the steps that follow provided that: 1. the samples are dependent and are obtained randomly and 2. the total number of observations where the 3. outcomes differ must be greater than or equal to 10. That is, f 12 + f 21 ≥ 10. © 2010 Pearson Prentice Hall. All rights reserved 222
Testing a Hypothesis Regarding the Difference of Two Population Proportions: Dependent Samples We can use the steps that follow provided that: 1. the samples are dependent and are obtained randomly and 2. the total number of observations where the 3. outcomes differ must be greater than or equal to 10. That is, f 12 + f 21 ≥ 10. © 2010 Pearson Prentice Hall. All rights reserved 222
 Step 1: Determine the null and alternative hypotheses. H 0: the proportions between the two populations are equal (p 1 = p 2) H 1: the proportions between the two populations differ (p 1 ≠ p 2) © 2010 Pearson Prentice Hall. All rights reserved 223
Step 1: Determine the null and alternative hypotheses. H 0: the proportions between the two populations are equal (p 1 = p 2) H 1: the proportions between the two populations differ (p 1 ≠ p 2) © 2010 Pearson Prentice Hall. All rights reserved 223
 Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 224
Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 224
 Step 3: Compute the test statistic © 2010 Pearson Prentice Hall. All rights reserved 225
Step 3: Compute the test statistic © 2010 Pearson Prentice Hall. All rights reserved 225
 Classical Approach Step 4: Use Table V to determine the critical value. This is a two tailed test. However, z 0 is always positive, so we only need to find the right critical value z /2. © 2010 Pearson Prentice Hall. All rights reserved 226
Classical Approach Step 4: Use Table V to determine the critical value. This is a two tailed test. However, z 0 is always positive, so we only need to find the right critical value z /2. © 2010 Pearson Prentice Hall. All rights reserved 226
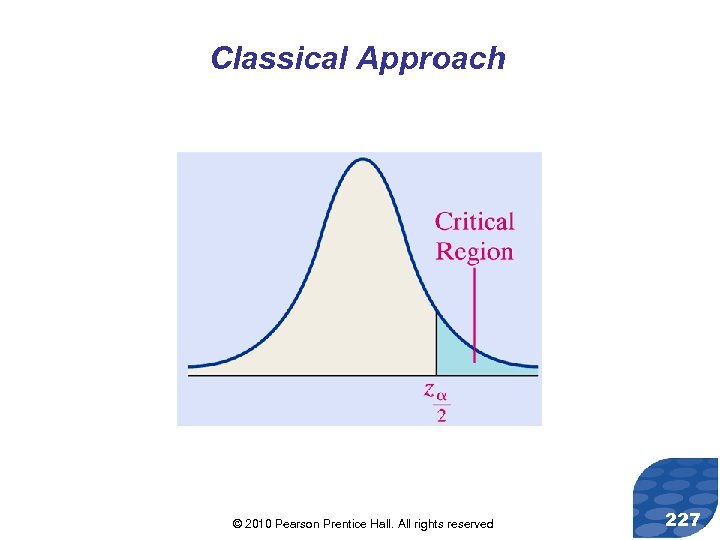 Classical Approach © 2010 Pearson Prentice Hall. All rights reserved 227
Classical Approach © 2010 Pearson Prentice Hall. All rights reserved 227
 Classical Approach Step 5: If z 0 > z /2, reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 228
Classical Approach Step 5: If z 0 > z /2, reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 228
 P-Value Approach Step 4: Use Table V to determine the P-value. . Because z 0 is always positive, we find the area to the right of z 0 and then double this area (since this is a two-tailed test). © 2010 Pearson Prentice Hall. All rights reserved 229
P-Value Approach Step 4: Use Table V to determine the P-value. . Because z 0 is always positive, we find the area to the right of z 0 and then double this area (since this is a two-tailed test). © 2010 Pearson Prentice Hall. All rights reserved 229
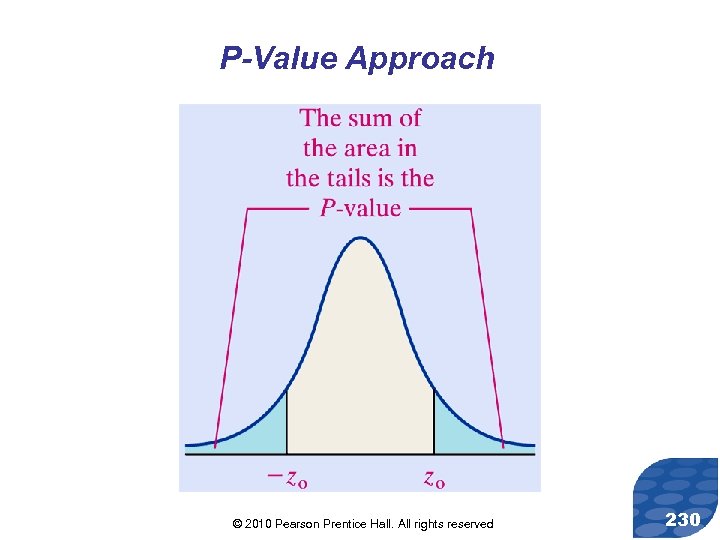 P-Value Approach © 2010 Pearson Prentice Hall. All rights reserved 230
P-Value Approach © 2010 Pearson Prentice Hall. All rights reserved 230
 P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 231
P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 231
 Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 232
Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 232
 Parallel Example 4: Analyzing the Difference of Two Proportions from Matched-Pairs Data A recent General Social Survey asked the following two questions of a random sample of 1483 adult Americans under the hypothetical scenario that the government suspected that a terrorist act was about to happen: • Do you believe the authorities should have the right to tap people’s telephone conversations? • Do you believe the authorities should have the right to detain people for as long as they want without putting them on trial? © 2010 Pearson Prentice Hall. All rights reserved 233
Parallel Example 4: Analyzing the Difference of Two Proportions from Matched-Pairs Data A recent General Social Survey asked the following two questions of a random sample of 1483 adult Americans under the hypothetical scenario that the government suspected that a terrorist act was about to happen: • Do you believe the authorities should have the right to tap people’s telephone conversations? • Do you believe the authorities should have the right to detain people for as long as they want without putting them on trial? © 2010 Pearson Prentice Hall. All rights reserved 233
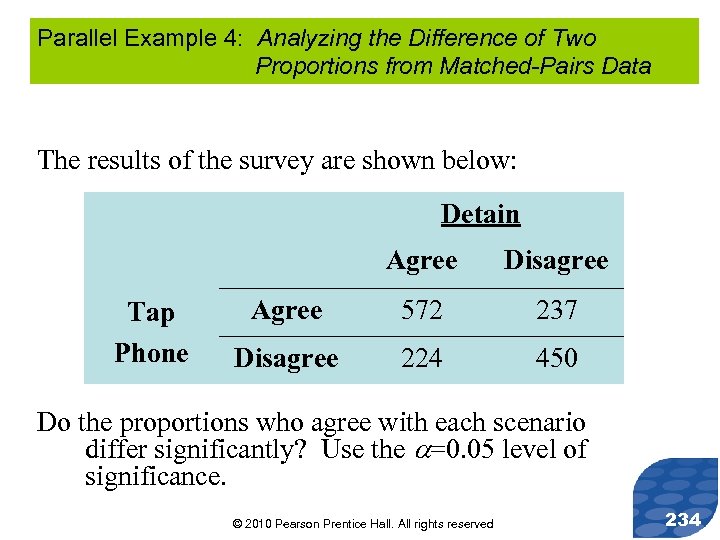 Parallel Example 4: Analyzing the Difference of Two Proportions from Matched-Pairs Data The results of the survey are shown below: Detain Agree Tap Phone Disagree Agree 572 237 Disagree 224 450 Do the proportions who agree with each scenario differ significantly? Use the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 234
Parallel Example 4: Analyzing the Difference of Two Proportions from Matched-Pairs Data The results of the survey are shown below: Detain Agree Tap Phone Disagree Agree 572 237 Disagree 224 450 Do the proportions who agree with each scenario differ significantly? Use the =0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 234
 Solution The sample proportion of individuals who believe that the authorities should be able to tap phones is. The sample proportion of individuals who believe that the authorities should have the right to detain people is. We want to determine whether the difference in sample proportions is due to sampling error or to the fact that the population proportions differ. © 2010 Pearson Prentice Hall. All rights reserved 235
Solution The sample proportion of individuals who believe that the authorities should be able to tap phones is. The sample proportion of individuals who believe that the authorities should have the right to detain people is. We want to determine whether the difference in sample proportions is due to sampling error or to the fact that the population proportions differ. © 2010 Pearson Prentice Hall. All rights reserved 235
 Solution The samples are dependent and were obtained randomly. The total number of individuals who agree with one scenario, but disagree with the other is 237+224=461, which is greater than 10. We can proceed with Mc. Nemar’s Test. Step 1: The hypotheses are as follows H 0: the proportions between the two populations are equal (p. T = p. D) H 1: the proportions between the two populations differ (p. T ≠ p. D) Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 236
Solution The samples are dependent and were obtained randomly. The total number of individuals who agree with one scenario, but disagree with the other is 237+224=461, which is greater than 10. We can proceed with Mc. Nemar’s Test. Step 1: The hypotheses are as follows H 0: the proportions between the two populations are equal (p. T = p. D) H 1: the proportions between the two populations differ (p. T ≠ p. D) Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 236
 Solution Step 3: The test statistic is: © 2010 Pearson Prentice Hall. All rights reserved 237
Solution Step 3: The test statistic is: © 2010 Pearson Prentice Hall. All rights reserved 237
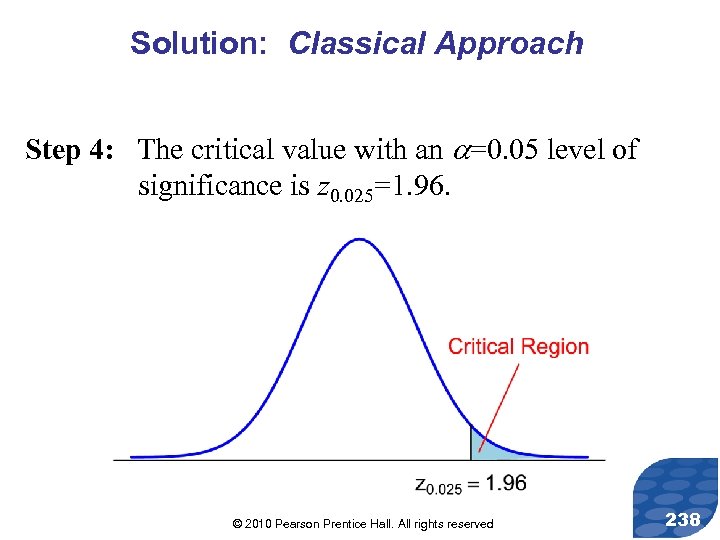 Solution: Classical Approach Step 4: The critical value with an =0. 05 level of significance is z 0. 025=1. 96. © 2010 Pearson Prentice Hall. All rights reserved 238
Solution: Classical Approach Step 4: The critical value with an =0. 05 level of significance is z 0. 025=1. 96. © 2010 Pearson Prentice Hall. All rights reserved 238
 Solution: Classical Approach Step 5: Since the test statistic, z 0=0. 56 is less than the critical value z. 025=1. 96, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 239
Solution: Classical Approach Step 5: Since the test statistic, z 0=0. 56 is less than the critical value z. 025=1. 96, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 239
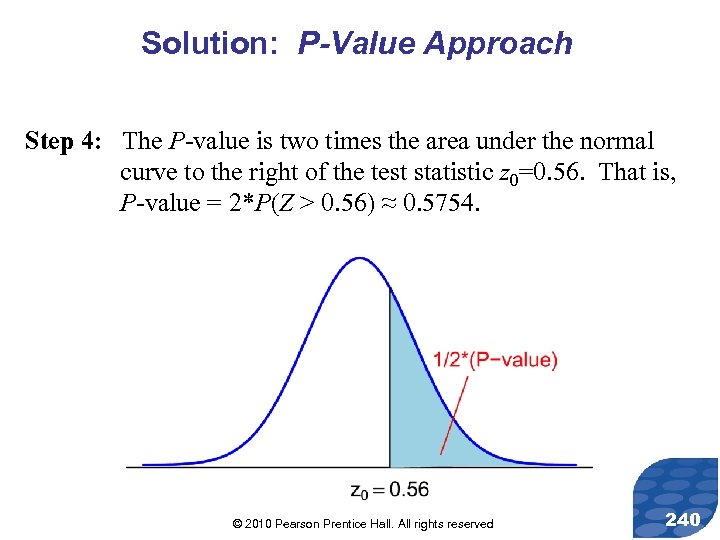 Solution: P-Value Approach Step 4: The P-value is two times the area under the normal curve to the right of the test statistic z 0=0. 56. That is, P-value = 2*P(Z > 0. 56) ≈ 0. 5754. © 2010 Pearson Prentice Hall. All rights reserved 240
Solution: P-Value Approach Step 4: The P-value is two times the area under the normal curve to the right of the test statistic z 0=0. 56. That is, P-value = 2*P(Z > 0. 56) ≈ 0. 5754. © 2010 Pearson Prentice Hall. All rights reserved 240
 Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance =0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 241
Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance =0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 241
 Solution Step 6: There is insufficient evidence at the =0. 05 level to conclude that there is a difference in the proportion of adult Americans who believe it is okay to phone tap versus detaining people for as long as they want without putting them on trial in the event that the government believed a terrorist plot was about to happen. © 2010 Pearson Prentice Hall. All rights reserved 242
Solution Step 6: There is insufficient evidence at the =0. 05 level to conclude that there is a difference in the proportion of adult Americans who believe it is okay to phone tap versus detaining people for as long as they want without putting them on trial in the event that the government believed a terrorist plot was about to happen. © 2010 Pearson Prentice Hall. All rights reserved 242
 Objective 4 • Determine the Sample Size Necessary for Estimating the Difference between Two Population Proportions within a Specified Margin of Error © 2010 Pearson Prentice Hall. All rights reserved 243
Objective 4 • Determine the Sample Size Necessary for Estimating the Difference between Two Population Proportions within a Specified Margin of Error © 2010 Pearson Prentice Hall. All rights reserved 243
 Sample Size for Estimating p 1 -p 2 The sample size required to obtain a (1 - ) 100% confidence interval with a margin of error, E, is given by rounded up to the next integer, if prior estimates of p 1 and p 2, , are available. If prior estimates of p 1 and p 2 are unavailable, the sample size is rounded up to the next integer. © 2010 Pearson Prentice Hall. All rights reserved 244
Sample Size for Estimating p 1 -p 2 The sample size required to obtain a (1 - ) 100% confidence interval with a margin of error, E, is given by rounded up to the next integer, if prior estimates of p 1 and p 2, , are available. If prior estimates of p 1 and p 2 are unavailable, the sample size is rounded up to the next integer. © 2010 Pearson Prentice Hall. All rights reserved 244
 Parallel Example 5: Determining Sample Size A doctor wants to estimate the difference in the proportion of 15 -19 year old mothers that received prenatal care and the proportion of 30 -34 year old mothers that received prenatal care. What sample size should be obtained if she wished the estimate to be within 2 percentage points with 95% confidence assuming: a) she uses the results of the National Vital Statistics Report results in which 98% of the 15 -19 year old mothers received prenatal care and 99. 2% of 30 -34 year old mothers received prenatal care. b) she does not use any prior estimates. © 2010 Pearson Prentice Hall. All rights reserved 245
Parallel Example 5: Determining Sample Size A doctor wants to estimate the difference in the proportion of 15 -19 year old mothers that received prenatal care and the proportion of 30 -34 year old mothers that received prenatal care. What sample size should be obtained if she wished the estimate to be within 2 percentage points with 95% confidence assuming: a) she uses the results of the National Vital Statistics Report results in which 98% of the 15 -19 year old mothers received prenatal care and 99. 2% of 30 -34 year old mothers received prenatal care. b) she does not use any prior estimates. © 2010 Pearson Prentice Hall. All rights reserved 245
 Solution We have E=0. 02 and z /2=z 0. 025=1. 96. a) Letting , The doctor must sample 265 randomly selected 15 -19 year old mothers and 265 randomly selected 30 -34 year old mothers. © 2010 Pearson Prentice Hall. All rights reserved 246
Solution We have E=0. 02 and z /2=z 0. 025=1. 96. a) Letting , The doctor must sample 265 randomly selected 15 -19 year old mothers and 265 randomly selected 30 -34 year old mothers. © 2010 Pearson Prentice Hall. All rights reserved 246
 Solution b) Without prior estimates of p 1 and p 2, the sample size is The doctor must sample 4802 randomly selected 15 -19 year old mothers and 4802 randomly selected 30 -34 year old mothers. Note that having prior estimates of p 1 and p 2 reduces the number of mothers that need to be surveyed. © 2010 Pearson Prentice Hall. All rights reserved 247
Solution b) Without prior estimates of p 1 and p 2, the sample size is The doctor must sample 4802 randomly selected 15 -19 year old mothers and 4802 randomly selected 30 -34 year old mothers. Note that having prior estimates of p 1 and p 2 reduces the number of mothers that need to be surveyed. © 2010 Pearson Prentice Hall. All rights reserved 247
 Section 11. 4 Inference about Two Population Standard Deviations © 2010 Pearson Prentice Hall. All rights reserved
Section 11. 4 Inference about Two Population Standard Deviations © 2010 Pearson Prentice Hall. All rights reserved
 Objectives 1. Find critical values of the F-distribution 2. Test hypotheses regarding two population standard deviations © 2010 Pearson Prentice Hall. All rights reserved 249
Objectives 1. Find critical values of the F-distribution 2. Test hypotheses regarding two population standard deviations © 2010 Pearson Prentice Hall. All rights reserved 249
 Objective 1 • Find Critical Values of the F-distribution © 2010 Pearson Prentice Hall. All rights reserved 250
Objective 1 • Find Critical Values of the F-distribution © 2010 Pearson Prentice Hall. All rights reserved 250
 Requirements for Testing Claims Regarding Two Population Standard Deviations 1. The samples are independent simple random samples. © 2010 Pearson Prentice Hall. All rights reserved 251
Requirements for Testing Claims Regarding Two Population Standard Deviations 1. The samples are independent simple random samples. © 2010 Pearson Prentice Hall. All rights reserved 251
 Requirements for Testing Claims Regarding Two Population Standard Deviations 1. The samples are independent simple random samples. 2. The populations from which the samples are drawn are normally distributed. © 2010 Pearson Prentice Hall. All rights reserved 252
Requirements for Testing Claims Regarding Two Population Standard Deviations 1. The samples are independent simple random samples. 2. The populations from which the samples are drawn are normally distributed. © 2010 Pearson Prentice Hall. All rights reserved 252
 CAUTION! If the populations from which the samples are drawn are not normal, do not use the inferential procedures discussed in this section. © 2010 Pearson Prentice Hall. All rights reserved 253
CAUTION! If the populations from which the samples are drawn are not normal, do not use the inferential procedures discussed in this section. © 2010 Pearson Prentice Hall. All rights reserved 253
 Notation Used When Comparing Two Population Standard Deviations : Variance for population 1 : Variance for population 2 : Sample variance for population 1 : Sample variance for population 2 n 1 : Sample size for population 1 n 2 : Sample size for population 2 © 2010 Pearson Prentice Hall. All rights reserved 254
Notation Used When Comparing Two Population Standard Deviations : Variance for population 1 : Variance for population 2 : Sample variance for population 1 : Sample variance for population 2 n 1 : Sample size for population 1 n 2 : Sample size for population 2 © 2010 Pearson Prentice Hall. All rights reserved 254
 Fisher's F-distribution If and are sample variances from independent simple random samples of size n 1 and n 2, respectively, drawn from normal populations, then follows the F-distribution with n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 255
Fisher's F-distribution If and are sample variances from independent simple random samples of size n 1 and n 2, respectively, drawn from normal populations, then follows the F-distribution with n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 255
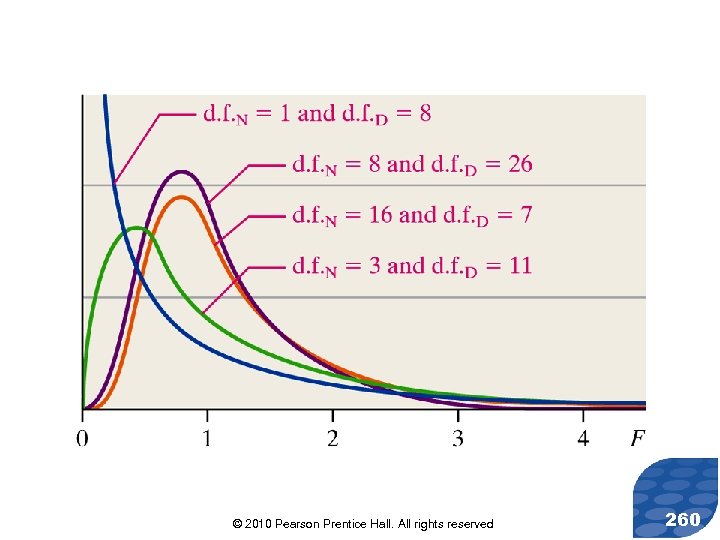
 Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. © 2010 Pearson Prentice Hall. All rights reserved 256
Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. © 2010 Pearson Prentice Hall. All rights reserved 256
 Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the 2 distribution and Student’s tdistribution, whose shapes depend upon their degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 257
Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the 2 distribution and Student’s tdistribution, whose shapes depend upon their degrees of freedom. © 2010 Pearson Prentice Hall. All rights reserved 257
 Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the distribution and Student’s tdistribution, whose shape depends upon their degrees of freedom. 3. The total area under the curve is 1. © 2010 Pearson Prentice Hall. All rights reserved 258
Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the distribution and Student’s tdistribution, whose shape depends upon their degrees of freedom. 3. The total area under the curve is 1. © 2010 Pearson Prentice Hall. All rights reserved 258
 Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the distribution and Student’s tdistribution, whose shape depends upon their degrees of freedom. 3. The total area under the curve is 1. 4. The values of F are always greater than or equal to zero. © 2010 Pearson Prentice Hall. All rights reserved 259
Characteristics of the F-distribution 1. It is not symmetric. The F-distribution is skewed right. 2. The shape of the F-distribution depends upon the degrees of freedom in the numerator and denominator. This is similar to the distribution and Student’s tdistribution, whose shape depends upon their degrees of freedom. 3. The total area under the curve is 1. 4. The values of F are always greater than or equal to zero. © 2010 Pearson Prentice Hall. All rights reserved 259
 © 2010 Pearson Prentice Hall. All rights reserved 260
© 2010 Pearson Prentice Hall. All rights reserved 260
 is the critical F with n 1 – 1 degrees of freedom in the numerator and n 2 – 1 degrees of freedom in the denominator and an area of to the right of the critical F. © 2010 Pearson Prentice Hall. All rights reserved 261
is the critical F with n 1 – 1 degrees of freedom in the numerator and n 2 – 1 degrees of freedom in the denominator and an area of to the right of the critical F. © 2010 Pearson Prentice Hall. All rights reserved 261
 To find the critical F with an area of α to the left, use the following: © 2010 Pearson Prentice Hall. All rights reserved 262
To find the critical F with an area of α to the left, use the following: © 2010 Pearson Prentice Hall. All rights reserved 262
 Parallel Example 1: Finding Critical Values for the F-distribution Find the critical F-value: a) for a right-tailed test with =0. 1, degrees of freedom in the numerator = 8 and degrees of freedom in the denominator = 4. b) for a two-tailed test with =0. 05, degrees of freedom in the numerator = 20 and degrees of freedom in the denominator = 15. © 2010 Pearson Prentice Hall. All rights reserved 263
Parallel Example 1: Finding Critical Values for the F-distribution Find the critical F-value: a) for a right-tailed test with =0. 1, degrees of freedom in the numerator = 8 and degrees of freedom in the denominator = 4. b) for a two-tailed test with =0. 05, degrees of freedom in the numerator = 20 and degrees of freedom in the denominator = 15. © 2010 Pearson Prentice Hall. All rights reserved 263
 Solution a) F 0. 1, 8, 4 = 3. 95 b) F. 025, 20, 15 = 2. 76; © 2010 Pearson Prentice Hall. All rights reserved = 0. 39 264
Solution a) F 0. 1, 8, 4 = 3. 95 b) F. 025, 20, 15 = 2. 76; © 2010 Pearson Prentice Hall. All rights reserved = 0. 39 264
 NOTE: If the number of degrees of freedom is not found in the table, we follow the practice of choosing the degrees of freedom closest to that desired. If the degrees of freedom is exactly between two values, find the mean of the values. © 2010 Pearson Prentice Hall. All rights reserved 265
NOTE: If the number of degrees of freedom is not found in the table, we follow the practice of choosing the degrees of freedom closest to that desired. If the degrees of freedom is exactly between two values, find the mean of the values. © 2010 Pearson Prentice Hall. All rights reserved 265
 Objective 2 • Test Hypotheses Regarding Two Population Standard Deviations © 2010 Pearson Prentice Hall. All rights reserved 266
Objective 2 • Test Hypotheses Regarding Two Population Standard Deviations © 2010 Pearson Prentice Hall. All rights reserved 266
 Test Hypotheses Regarding Two Population Standard Deviations To test hypotheses regarding two population standard deviations, 1 and 2, we can use the following steps, provided that 1. the samples are obtained using simple random sampling, 2. the sample data are independent, and 3. the populations from which the samples are drawn are normally distributed. © 2010 Pearson Prentice Hall. All rights reserved 267
Test Hypotheses Regarding Two Population Standard Deviations To test hypotheses regarding two population standard deviations, 1 and 2, we can use the following steps, provided that 1. the samples are obtained using simple random sampling, 2. the sample data are independent, and 3. the populations from which the samples are drawn are normally distributed. © 2010 Pearson Prentice Hall. All rights reserved 267
 Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways: Two-Tailed Left-Tailed Right-Tailed H 0: 1 = 2 H 1: 1 ≠ 2 H 1: 1 < 2 H 1: 1 > 2 Note: 1 is the population standard deviation for population 1 and 2 is the population standard deviation for population 2. © 2010 Pearson Prentice Hall. All rights reserved 268
Step 1: Determine the null and alternative hypotheses. The hypotheses can be structured in one of three ways: Two-Tailed Left-Tailed Right-Tailed H 0: 1 = 2 H 1: 1 ≠ 2 H 1: 1 < 2 H 1: 1 > 2 Note: 1 is the population standard deviation for population 1 and 2 is the population standard deviation for population 2. © 2010 Pearson Prentice Hall. All rights reserved 268
 Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 269
Step 2: Select a level of significance, , based on the seriousness of making a Type I error. © 2010 Pearson Prentice Hall. All rights reserved 269
 Step 3: Compute the test statistic which follows Fisher’s F-distribution with n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 270
Step 3: Compute the test statistic which follows Fisher’s F-distribution with n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 270
 Classical Approach Step 4: Use Table VIII to determine the critical value(s) using n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 271
Classical Approach Step 4: Use Table VIII to determine the critical value(s) using n 1 -1 degrees of freedom in the numerator and n 2 -1 degrees of freedom in the denominator. © 2010 Pearson Prentice Hall. All rights reserved 271
 Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 272
Classical Approach Two-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 272
 Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 273
Classical Approach Left-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 273
 Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 274
Classical Approach Right-Tailed (critical value) © 2010 Pearson Prentice Hall. All rights reserved 274
 Classical Approach Step 5: Compare the critical value with the test statistic: Two-Tailed If or reject the null hypothesis. Left-Tailed If , reject the null hypothesis. Right-Tailed , If reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved , 275
Classical Approach Step 5: Compare the critical value with the test statistic: Two-Tailed If or reject the null hypothesis. Left-Tailed If , reject the null hypothesis. Right-Tailed , If reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved , 275
 P-Value Approach Step 4: Use technology to determine the P-value. © 2010 Pearson Prentice Hall. All rights reserved 276
P-Value Approach Step 4: Use technology to determine the P-value. © 2010 Pearson Prentice Hall. All rights reserved 276
 P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 277
P-Value Approach Step 5: If P-value < , reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 277
 Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 278
Step 6: State the conclusion. © 2010 Pearson Prentice Hall. All rights reserved 278
 CAUTION! The procedures just presented are not robust, minor departures from normality will adversely affect the results of the test. Therefore, the test should be used only when the requirement of normality has been verified. © 2010 Pearson Prentice Hall. All rights reserved 279
CAUTION! The procedures just presented are not robust, minor departures from normality will adversely affect the results of the test. Therefore, the test should be used only when the requirement of normality has been verified. © 2010 Pearson Prentice Hall. All rights reserved 279
 Parallel Example 2: Testing Hypotheses Regarding Two Population Standard Deviations A researcher wanted to know whether “state” quarters had a standard deviation weight that is less than “traditional” quarters. He randomly selected 18 “state” quarters and 16 “traditional” quarters, weighed each of them and obtained the data on the next slide. A normal probability plot indicates that the sample data could come from a population that is normal. Test the researcher’s claim at the = 0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 280
Parallel Example 2: Testing Hypotheses Regarding Two Population Standard Deviations A researcher wanted to know whether “state” quarters had a standard deviation weight that is less than “traditional” quarters. He randomly selected 18 “state” quarters and 16 “traditional” quarters, weighed each of them and obtained the data on the next slide. A normal probability plot indicates that the sample data could come from a population that is normal. Test the researcher’s claim at the = 0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 280
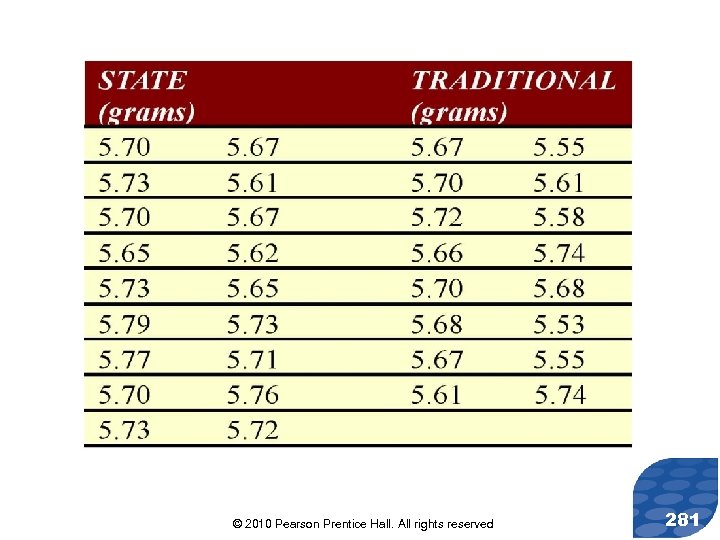 © 2010 Pearson Prentice Hall. All rights reserved 281
© 2010 Pearson Prentice Hall. All rights reserved 281
 Solution Step 1: The researcher wants to know if “state” quarters have a standard deviation weight that is less than “traditional” quarters. Thus H 0: 1= 2 versus H 1: 1< 2 This is a left-tailed test. Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 282
Solution Step 1: The researcher wants to know if “state” quarters have a standard deviation weight that is less than “traditional” quarters. Thus H 0: 1= 2 versus H 1: 1< 2 This is a left-tailed test. Step 2: The level of significance is = 0. 05. © 2010 Pearson Prentice Hall. All rights reserved 282
 Solution Step 3: The standard deviation of “state” quarters was found to be 0. 0497 and the standard deviation of “traditional” quarters was found to be 0. 0689. The test statistic is then © 2010 Pearson Prentice Hall. All rights reserved 283
Solution Step 3: The standard deviation of “state” quarters was found to be 0. 0497 and the standard deviation of “traditional” quarters was found to be 0. 0689. The test statistic is then © 2010 Pearson Prentice Hall. All rights reserved 283
 Solution: Classical Approach Step 4: Since this is a left-tailed test, we determine the critical value at the 1 - = 1 -0. 05 = 0. 95 level of significance with n 1 -1=18 -1=17 degrees of freedom in the numerator and n 2 -1=16 -1=15 degrees of freedom in the denominator. Thus, Note: we used the table value F 0. 05, 15 for the above calculation since this is the closest to the required degrees of freedom available from Table VIII. © 2010 Pearson Prentice Hall. All rights reserved 284
Solution: Classical Approach Step 4: Since this is a left-tailed test, we determine the critical value at the 1 - = 1 -0. 05 = 0. 95 level of significance with n 1 -1=18 -1=17 degrees of freedom in the numerator and n 2 -1=16 -1=15 degrees of freedom in the denominator. Thus, Note: we used the table value F 0. 05, 15 for the above calculation since this is the closest to the required degrees of freedom available from Table VIII. © 2010 Pearson Prentice Hall. All rights reserved 284
 Solution: Classical Approach Step 5: Since the test statistic F 0= 0. 52 is greater than the critical value F 0. 95, 17, 15=0. 42, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 285
Solution: Classical Approach Step 5: Since the test statistic F 0= 0. 52 is greater than the critical value F 0. 95, 17, 15=0. 42, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 285
 Solution: P-Value Approach Step 4: Using technology, we find that the P-value is 0. 097. If the statement in the null hypothesis were true, we would expect to get the results obtained about 10 out of 100 times. This is not very unusual. © 2010 Pearson Prentice Hall. All rights reserved 286
Solution: P-Value Approach Step 4: Using technology, we find that the P-value is 0. 097. If the statement in the null hypothesis were true, we would expect to get the results obtained about 10 out of 100 times. This is not very unusual. © 2010 Pearson Prentice Hall. All rights reserved 286
 Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance, = 0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 287
Solution: P-Value Approach Step 5: Since the P-value is greater than the level of significance, = 0. 05, we fail to reject the null hypothesis. © 2010 Pearson Prentice Hall. All rights reserved 287
 Solution Step 6: There is not enough evidence to conclude that the standard deviation of weight is less for “state” quarters than it is for “traditional” quarters at the = 0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 288
Solution Step 6: There is not enough evidence to conclude that the standard deviation of weight is less for “state” quarters than it is for “traditional” quarters at the = 0. 05 level of significance. © 2010 Pearson Prentice Hall. All rights reserved 288
 Section 11. 5 Putting It Together: Which Method Do I Use? © 2010 Pearson Prentice Hall. All rights reserved
Section 11. 5 Putting It Together: Which Method Do I Use? © 2010 Pearson Prentice Hall. All rights reserved
 Objectives 1. Determine the appropriate hypothesis test to perform © 2010 Pearson Prentice Hall. All rights reserved 290
Objectives 1. Determine the appropriate hypothesis test to perform © 2010 Pearson Prentice Hall. All rights reserved 290
 Objective 1 • Determine the Appropriate Hypothesis Test to Perform © 2010 Pearson Prentice Hall. All rights reserved 291
Objective 1 • Determine the Appropriate Hypothesis Test to Perform © 2010 Pearson Prentice Hall. All rights reserved 291
 What parameter is addressed in the hypothesis? • Proportion, p • or 2 • Mean, © 2010 Pearson Prentice Hall. All rights reserved 292
What parameter is addressed in the hypothesis? • Proportion, p • or 2 • Mean, © 2010 Pearson Prentice Hall. All rights reserved 292
 Proportion, p Is the sampling Dependent or Independent? © 2010 Pearson Prentice Hall. All rights reserved 293
Proportion, p Is the sampling Dependent or Independent? © 2010 Pearson Prentice Hall. All rights reserved 293
 Proportion, p Dependent samples: Provided the samples are obtained randomly and the total number of observations where the outcomes differ is at least 10, use the normal distribution with © 2010 Pearson Prentice Hall. All rights reserved 294
Proportion, p Dependent samples: Provided the samples are obtained randomly and the total number of observations where the outcomes differ is at least 10, use the normal distribution with © 2010 Pearson Prentice Hall. All rights reserved 294
 Proportion, p Independent samples: Provided for each sample and the sample size is no more than 5% of the population size, use the normal distribution with where © 2010 Pearson Prentice Hall. All rights reserved 295
Proportion, p Independent samples: Provided for each sample and the sample size is no more than 5% of the population size, use the normal distribution with where © 2010 Pearson Prentice Hall. All rights reserved 295
 or 2 Provided the data are normally distributed, use the F-distribution with © 2010 Pearson Prentice Hall. All rights reserved 296
or 2 Provided the data are normally distributed, use the F-distribution with © 2010 Pearson Prentice Hall. All rights reserved 296
 Mean, Is the sampling Dependent or Independent? © 2010 Pearson Prentice Hall. All rights reserved 297
Mean, Is the sampling Dependent or Independent? © 2010 Pearson Prentice Hall. All rights reserved 297
 Mean, Dependent samples: Provided each sample size is greater than 30 or the differences come from a population that is normally distributed, use Student’s t-distribution with n-1 degrees of freedom with © 2010 Pearson Prentice Hall. All rights reserved 298
Mean, Dependent samples: Provided each sample size is greater than 30 or the differences come from a population that is normally distributed, use Student’s t-distribution with n-1 degrees of freedom with © 2010 Pearson Prentice Hall. All rights reserved 298
 Mean, Independent samples: Provided each sample size is greater than 30 or each population is normally distributed, use Student’s t-distribution © 2010 Pearson Prentice Hall. All rights reserved 299
Mean, Independent samples: Provided each sample size is greater than 30 or each population is normally distributed, use Student’s t-distribution © 2010 Pearson Prentice Hall. All rights reserved 299


