Chapter 10 Inferences on Two Samples 10 1

Chapter 10 Inferences on Two Samples 10. 1 Inference about Means: Dependent Sampling

A sampling method is independent when the individuals selected for one sample does not dictate which individuals are to be in a second sample. A sampling method is dependent when the individuals selected to be in one sample are used to determine the individuals to be in the second sample. Dependent samples are often referred to as matched pairs samples.

EXAMPLE Independent versus Dependent Sampling For each of the following, determine whether the sampling method is independent or dependent. (a) A researcher wants to know whether the price of a one night stay at a Holiday Inn Express Hotel is less than the price of a one night stay at a Red Roof Inn Hotel. She randomly selects 8 towns where the location of the hotels is close to each other and determines the price of a one night stay. (b) A researcher wants to know whether the newly issued “state” quarters have a mean weight that is different from “traditional” quarters. He randomly selects 18 “state” quarters and 16 “traditional” quarters. Their weights are compared.

In order to test the hypotheses regarding the mean difference, we need certain requirements to be satisfied. • A simple random sample is obtained • the sample data is matched pairs • the differences are normally distributed or the sample size, n, is large (n > 30).

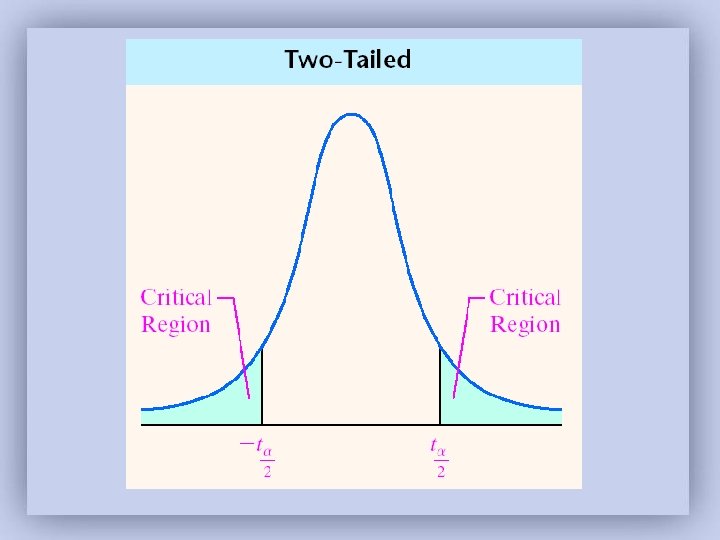
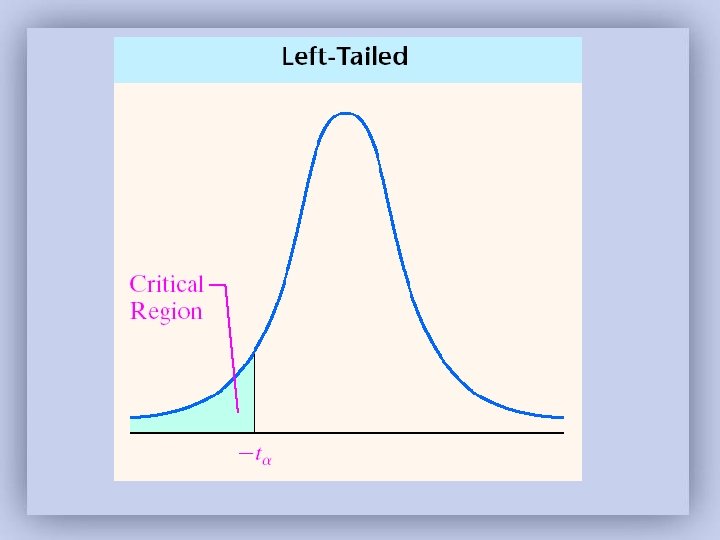
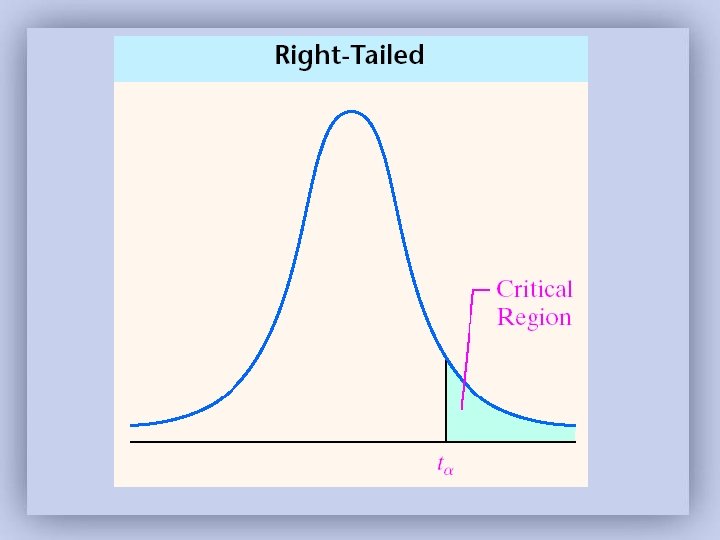
Step 4: Compare the critical value with the test statistic:

Step 5 : State the conclusion.

EXAMPLE Testing a Claim Regarding Matched Pairs Data

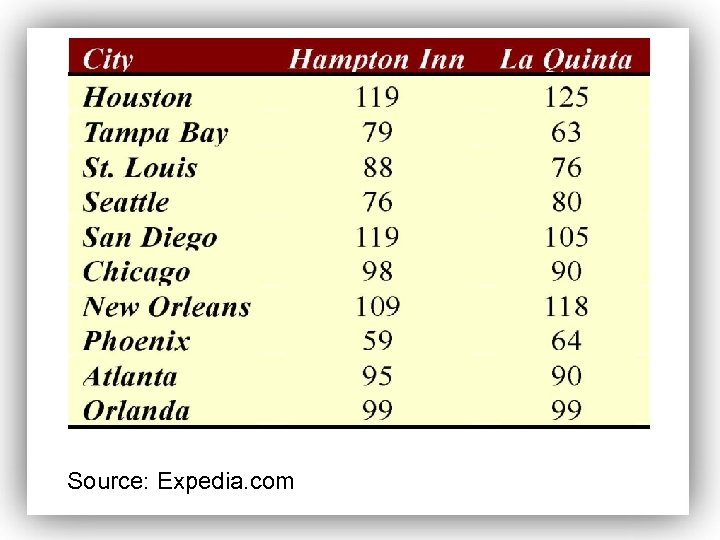Source: Expedia. com

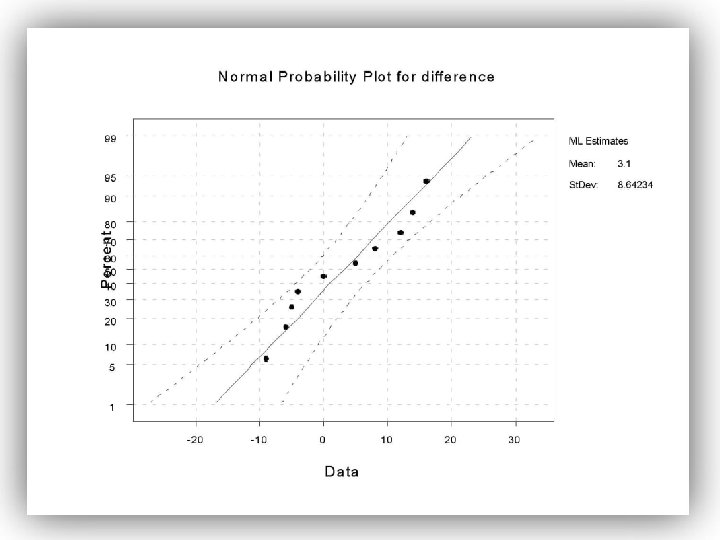
Test Hypothesis • Is the differences distribution normally distributed? • Step 1. Structure the Hypothesis H 0: u=0 H 1: u ≠ 0 Step 2 give α=0. 05 Critical values t=2. 26216 C=(2. 26216, infinity) Step 3 Test Statistic d=31, s=9. 11

• Step 4. t is in the critical region. • Step 5. Conclusion: No evidence support H 0

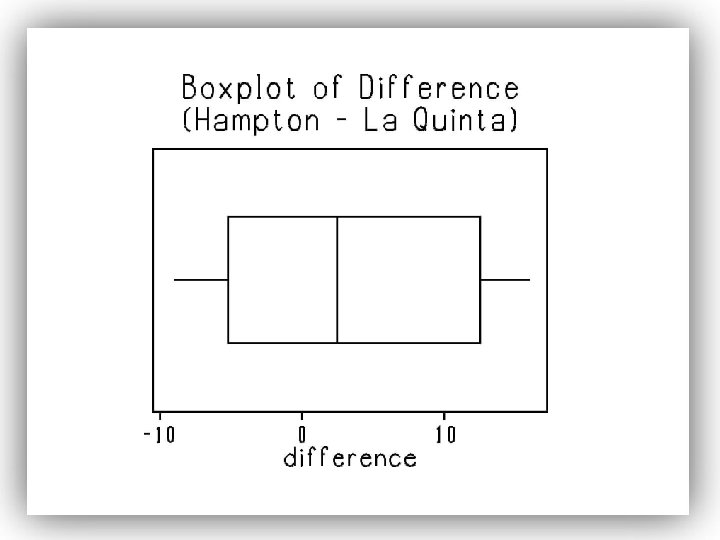
EXAMPLE Constructing a Confidence Interval for the Mean Difference Construct a 90% confidence interval for the mean difference in price of Hampton Inn versus La Quinta hotel rooms.

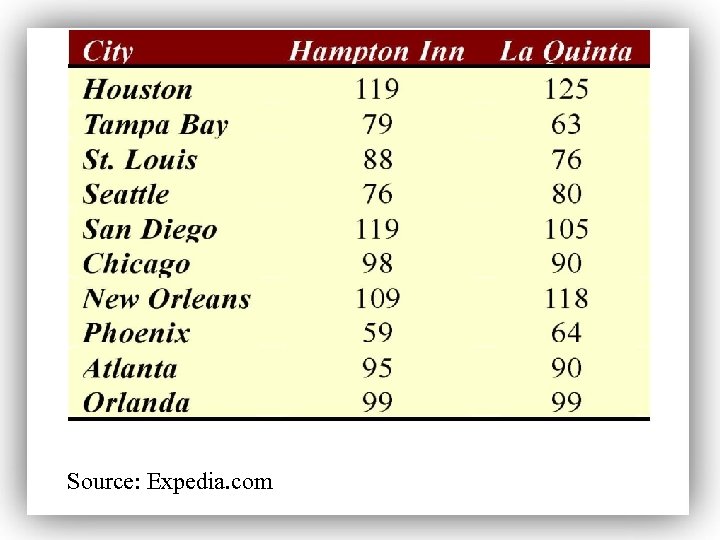Source: Expedia. com

Chapter 10 Inferences on Two Samples 10. 2 Inference about Two Means: Independent Sampling

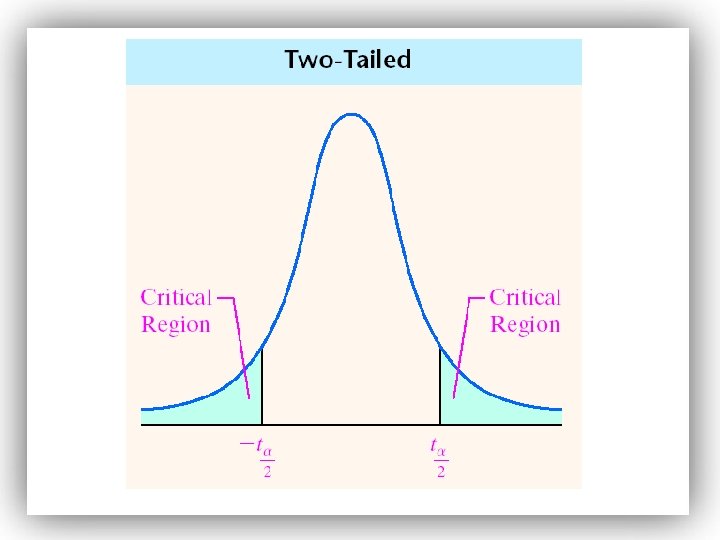
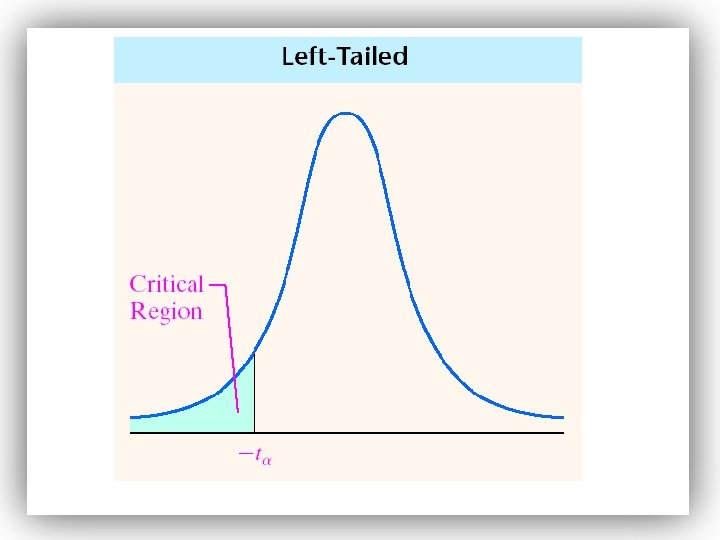
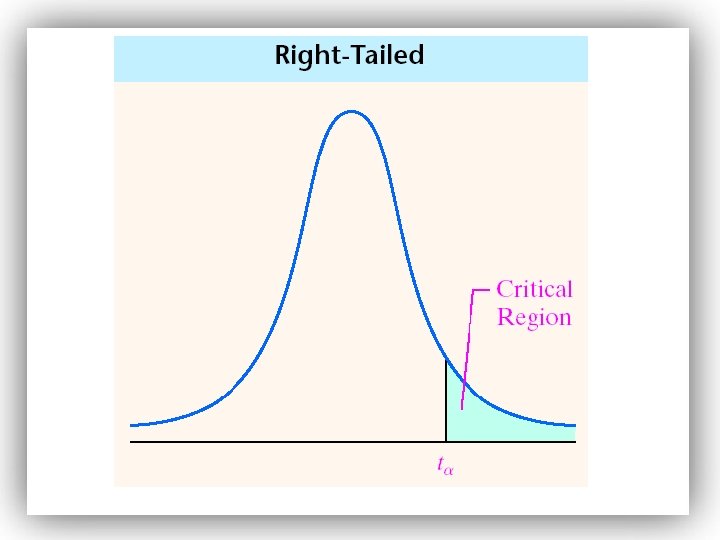
Step 4: Compare the critical value with the test statistic:

Step 5 : State the conclusion.

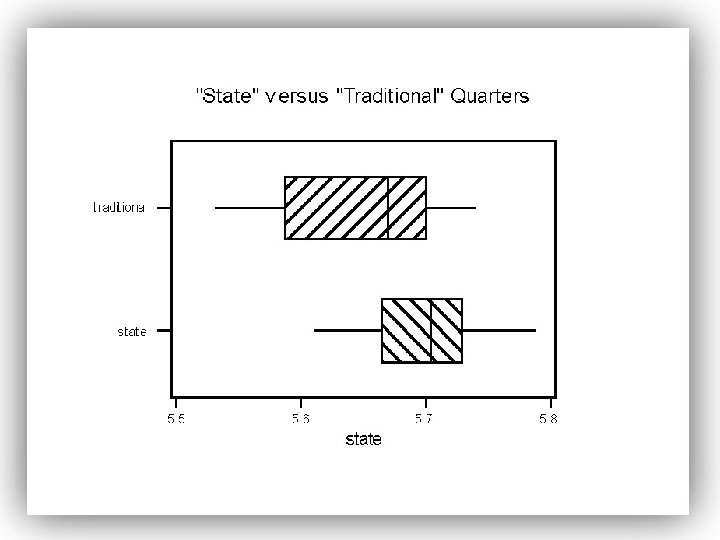
EXAMPLE Comparing Two Means: Independent Sampling A researcher wanted to know whether “state” quarters had a weight that is more than “traditional” quarters. He randomly selected 18 “state” quarters and 16 “traditional” quarters, weighed each of them and obtained the following data.

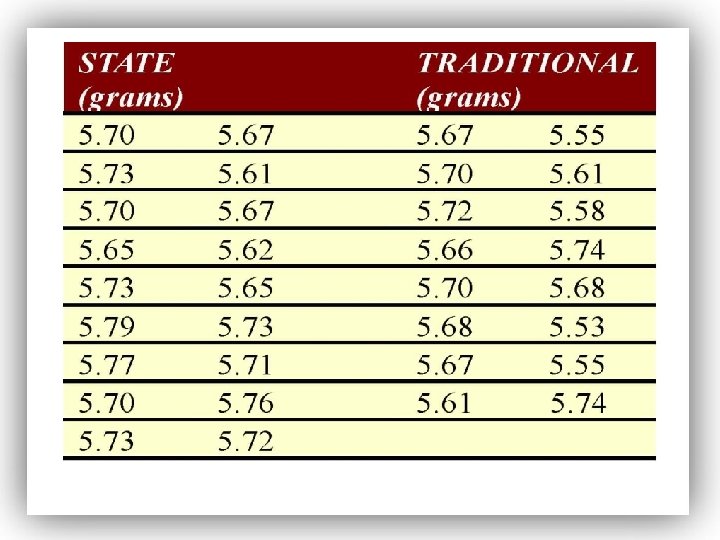
The degrees of freedom used to determine the critical value(s) presented in the last example are conservative. Results that are more accurate can be obtained by using the following degrees of freedom:

Lower Bound = Upper Bound =

EXAMPLE Constructing a Confidence Interval about the Difference of Two Means Construct a 95% confidence interval about the difference between the weight of “state” quarters and “traditional” quarters.