 Chapter 10 Hypothesis Testing
Chapter 10 Hypothesis Testing
 Chapter Goals
Chapter Goals
 What is a Hypothesis?
What is a Hypothesis?
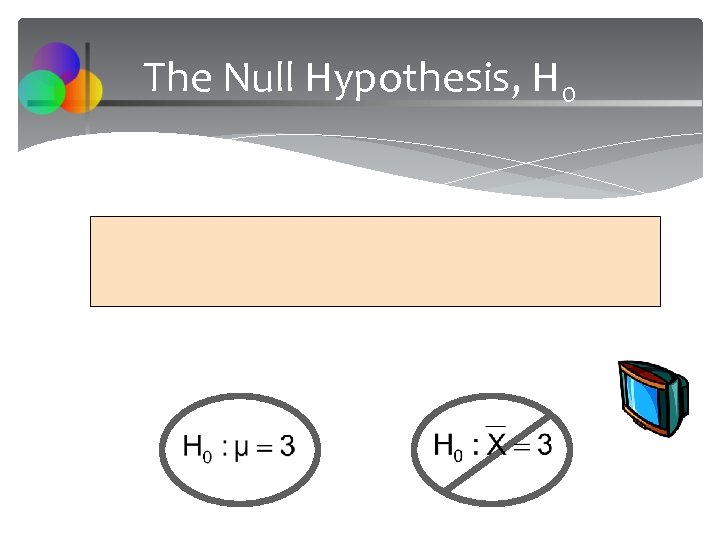 The Null Hypothesis, H 0
The Null Hypothesis, H 0
 The Null Hypothesis, H 0
The Null Hypothesis, H 0
 The Alternative Hypothesis, H 1
The Alternative Hypothesis, H 1
 Is
Is
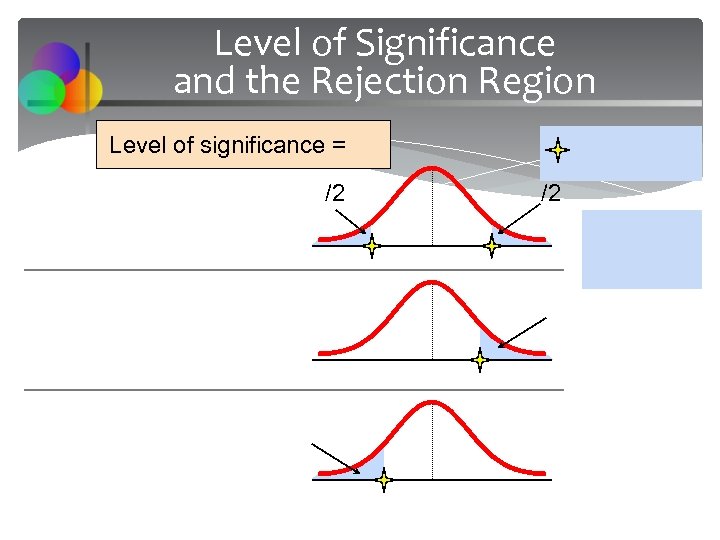 Level of Significance and the Rejection Region Level of significance = /2 /2
Level of Significance and the Rejection Region Level of significance = /2 /2
 Errors in Making Decisions
Errors in Making Decisions
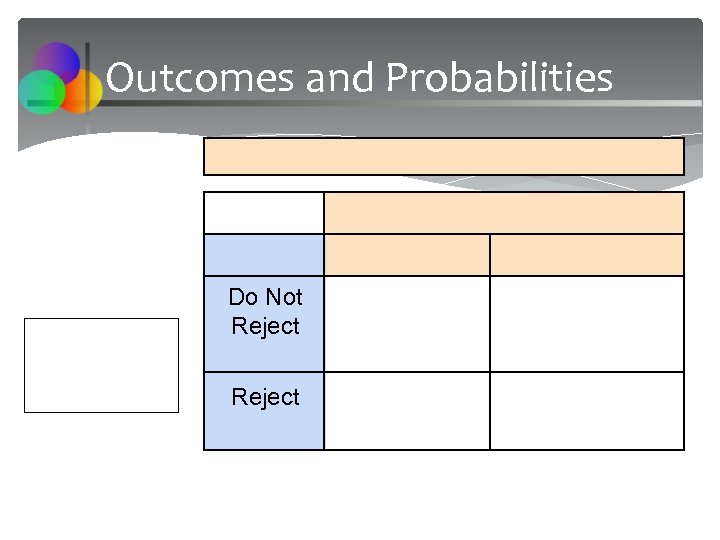 Outcomes and Probabilities Do Not Reject
Outcomes and Probabilities Do Not Reject
 Power of the Test
Power of the Test
 Hypothesis Tests for the Mean
Hypothesis Tests for the Mean
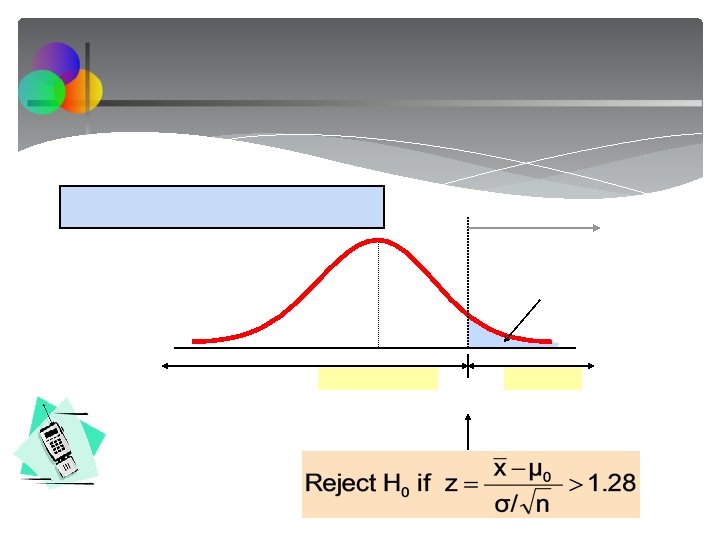
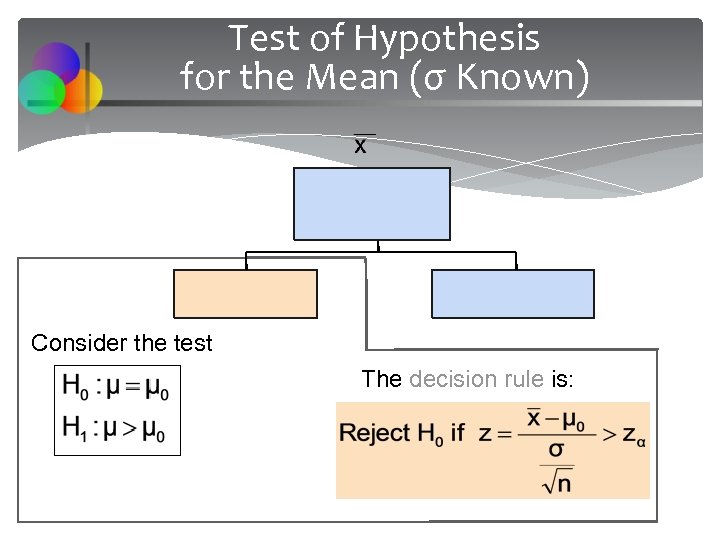 Test of Hypothesis for the Mean (σ Known) Consider the test The decision rule is:
Test of Hypothesis for the Mean (σ Known) Consider the test The decision rule is:
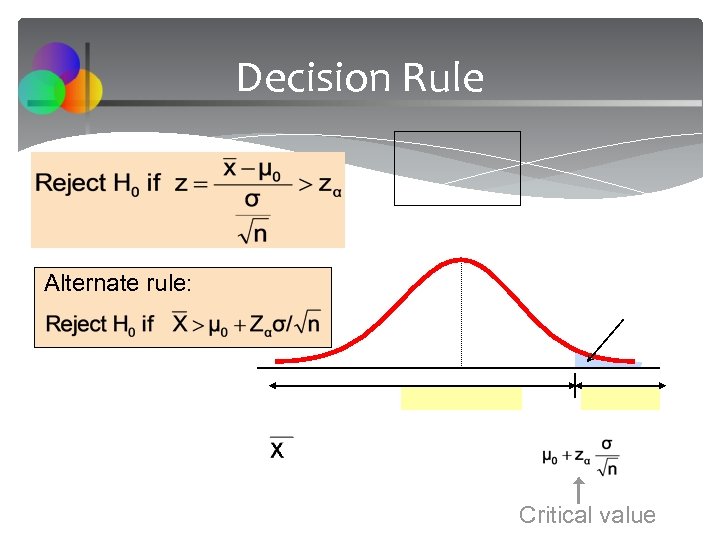 Decision Rule Alternate rule: Critical value
Decision Rule Alternate rule: Critical value
 p-Value Approach to Testing
p-Value Approach to Testing
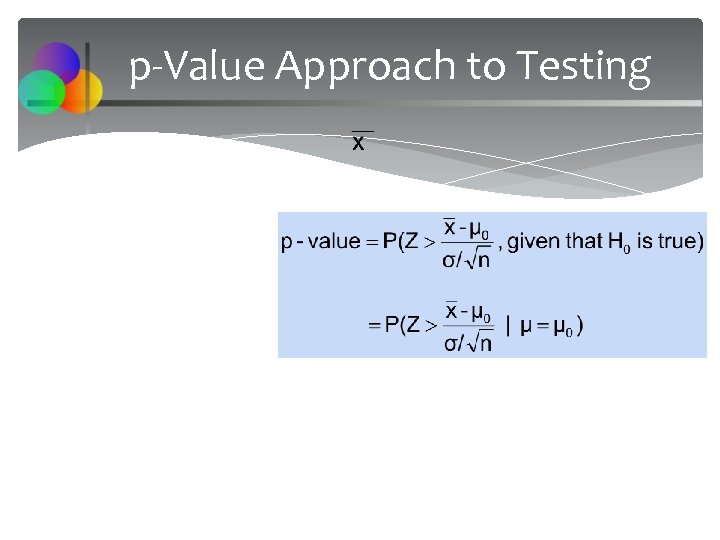 p-Value Approach to Testing
p-Value Approach to Testing
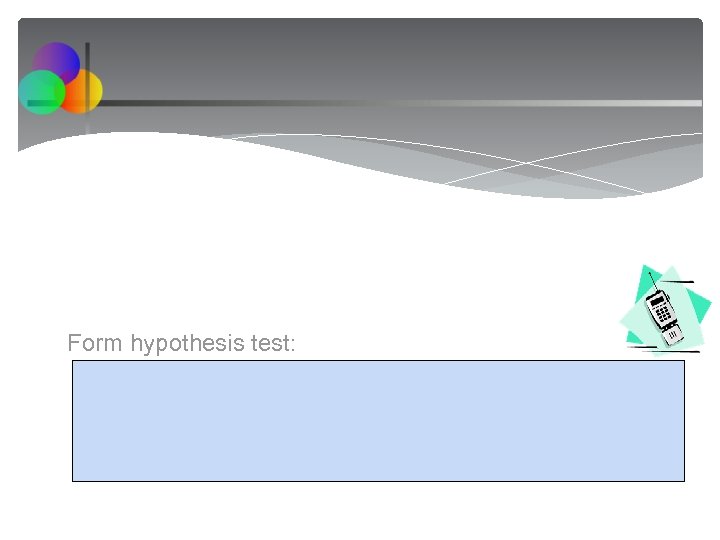 Form hypothesis test:
Form hypothesis test:
 Chap 10 -19
Chap 10 -19
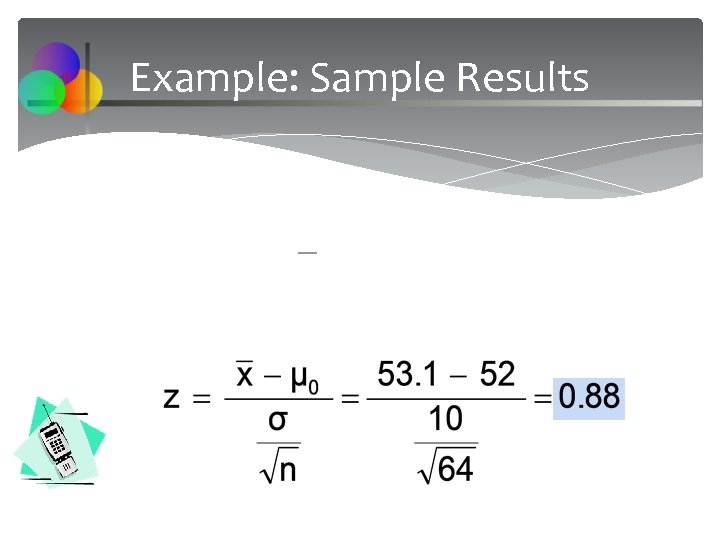 Example: Sample Results
Example: Sample Results
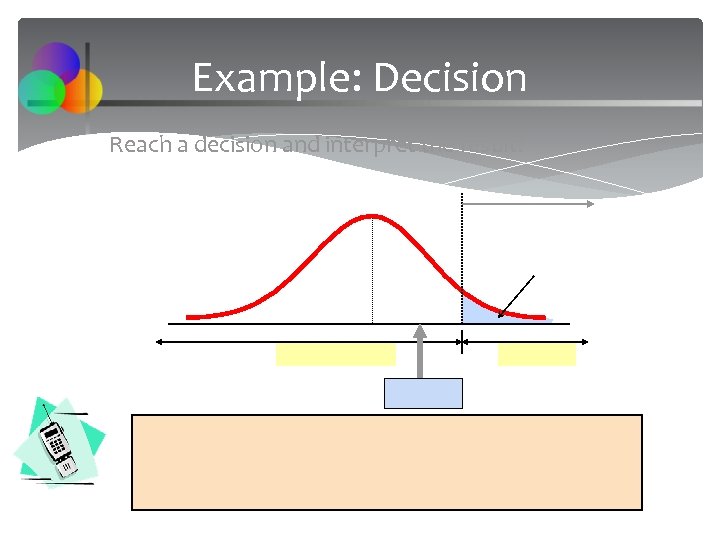 Example: Decision Reach a decision and interpret the result:
Example: Decision Reach a decision and interpret the result:
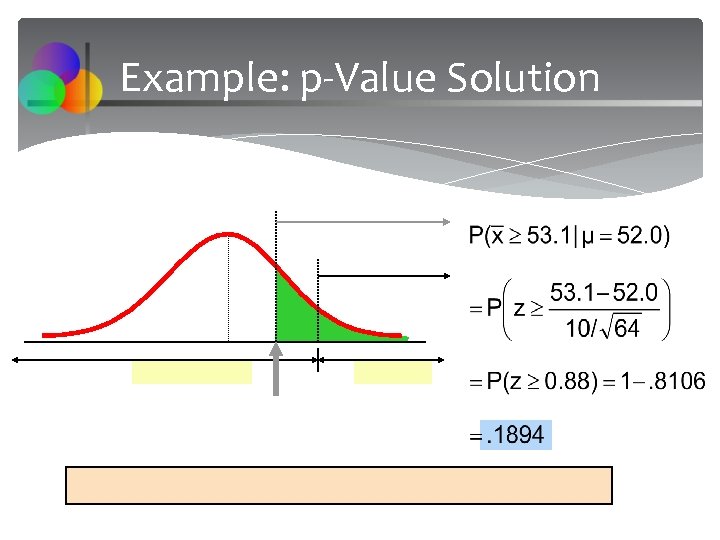 Example: p-Value Solution
Example: p-Value Solution
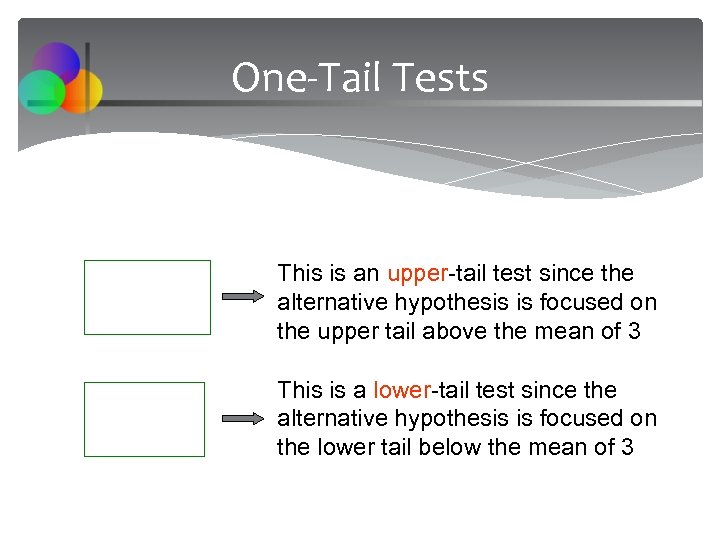 One-Tail Tests This is an upper-tail test since the alternative hypothesis is focused on the upper tail above the mean of 3 This is a lower-tail test since the alternative hypothesis is focused on the lower tail below the mean of 3
One-Tail Tests This is an upper-tail test since the alternative hypothesis is focused on the upper tail above the mean of 3 This is a lower-tail test since the alternative hypothesis is focused on the lower tail below the mean of 3
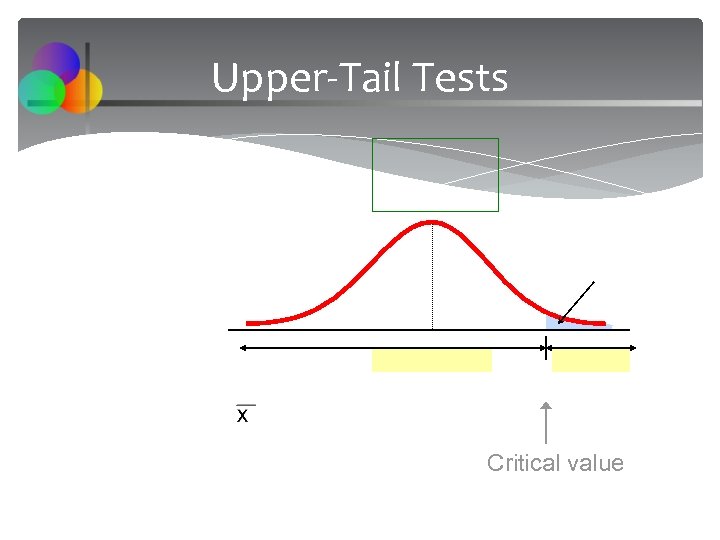 Upper-Tail Tests Critical value
Upper-Tail Tests Critical value
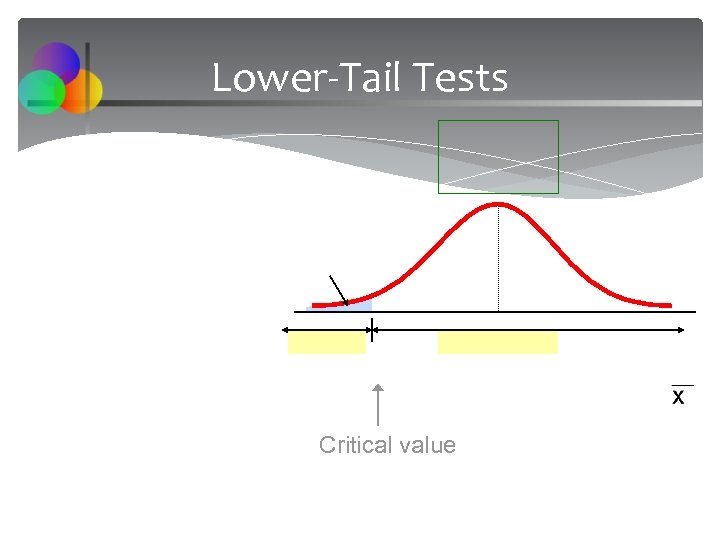 Lower-Tail Tests Critical value
Lower-Tail Tests Critical value
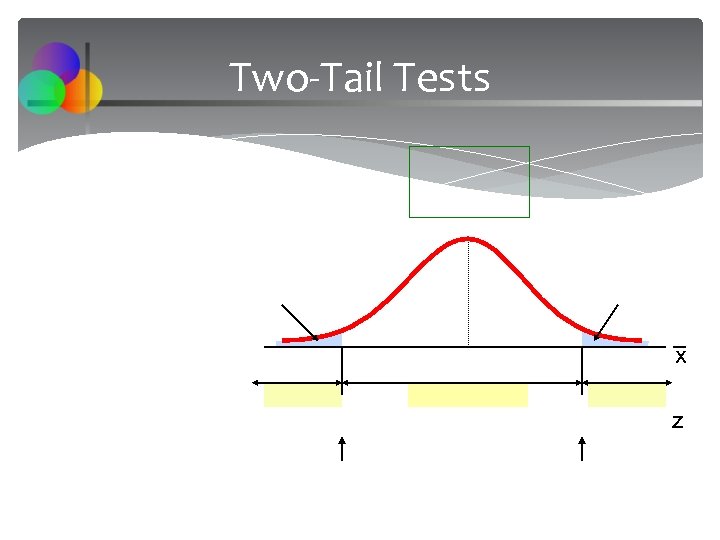 Two-Tail Tests x z
Two-Tail Tests x z
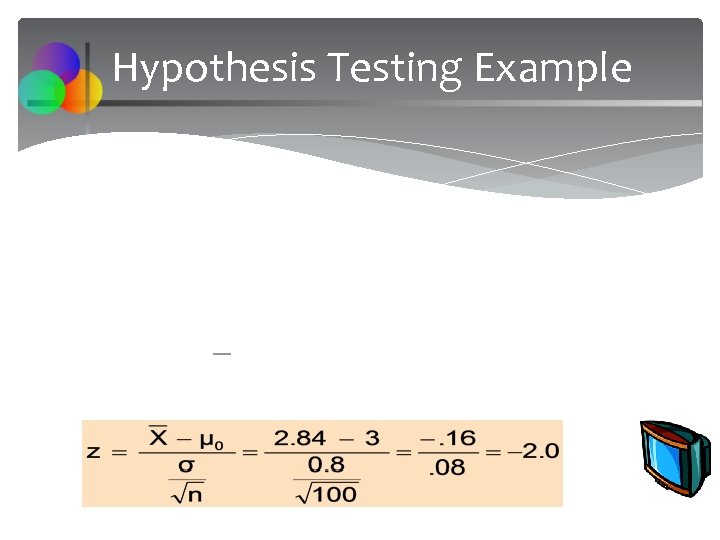
 Hypothesis Testing Example
Hypothesis Testing Example
 Hypothesis Testing Example
Hypothesis Testing Example
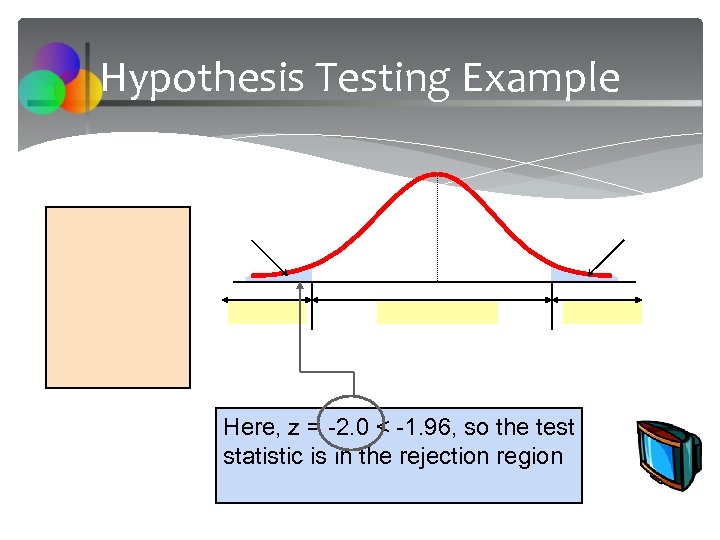 Hypothesis Testing Example Here, z = -2. 0 < -1. 96, so the test statistic is in the rejection region
Hypothesis Testing Example Here, z = -2. 0 < -1. 96, so the test statistic is in the rejection region
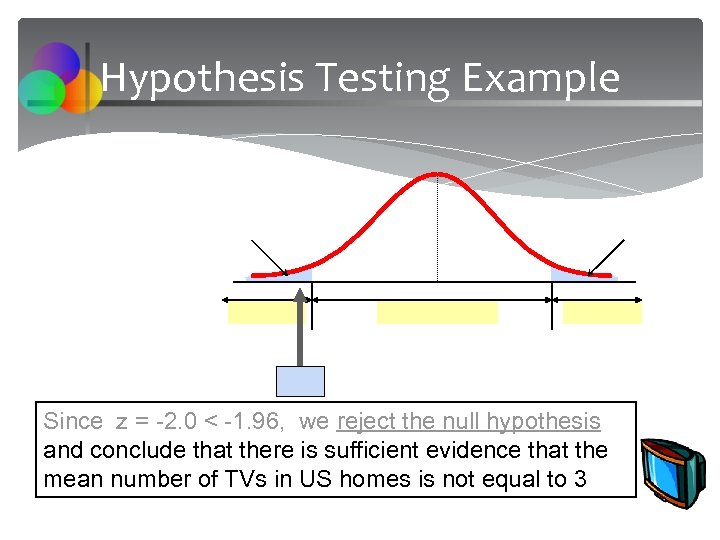 Hypothesis Testing Example Since z = -2. 0 < -1. 96, we reject the null hypothesis and conclude that there is sufficient evidence that the mean number of TVs in US homes is not equal to 3
Hypothesis Testing Example Since z = -2. 0 < -1. 96, we reject the null hypothesis and conclude that there is sufficient evidence that the mean number of TVs in US homes is not equal to 3
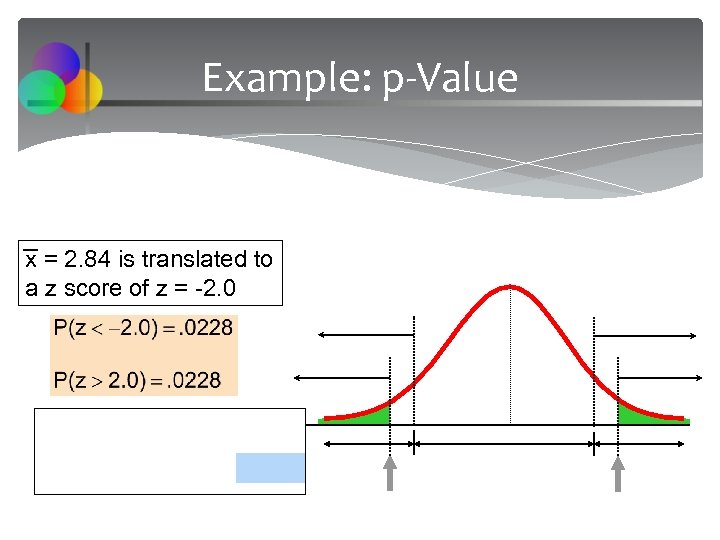 Example: p-Value x = 2. 84 is translated to a z score of z = -2. 0
Example: p-Value x = 2. 84 is translated to a z score of z = -2. 0
 Example: p-Value
Example: p-Value
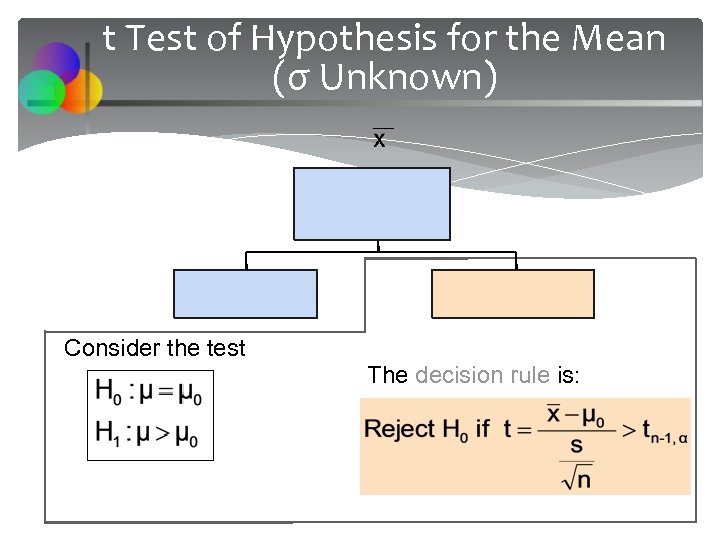 t Test of Hypothesis for the Mean (σ Unknown) Consider the test The decision rule is:
t Test of Hypothesis for the Mean (σ Unknown) Consider the test The decision rule is:
 t Test of Hypothesis for the Mean (σ Unknown) Consider the test The decision rule is:
t Test of Hypothesis for the Mean (σ Unknown) Consider the test The decision rule is:
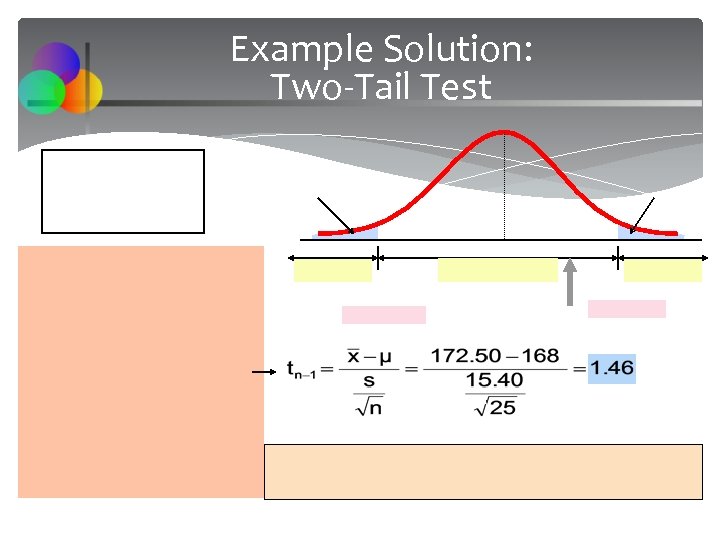 Example Solution: Two-Tail Test
Example Solution: Two-Tail Test
 Tests of the Population Proportion
Tests of the Population Proportion
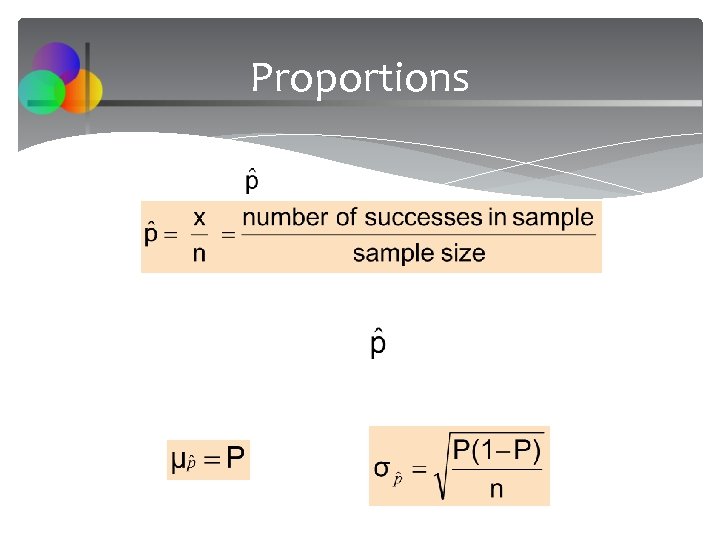 Proportions
Proportions
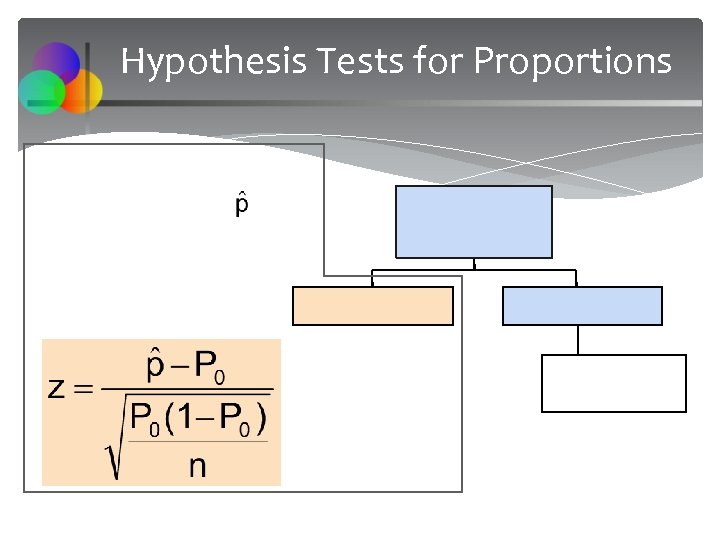 Hypothesis Tests for Proportions
Hypothesis Tests for Proportions
 Example: Z Test for Proportion
Example: Z Test for Proportion
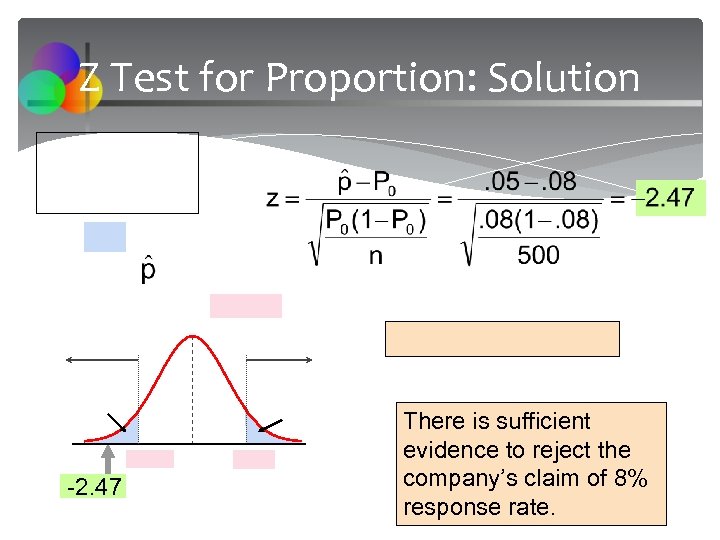 Z Test for Proportion: Solution -2. 47 There is sufficient evidence to reject the company’s claim of 8% response rate.
Z Test for Proportion: Solution -2. 47 There is sufficient evidence to reject the company’s claim of 8% response rate.
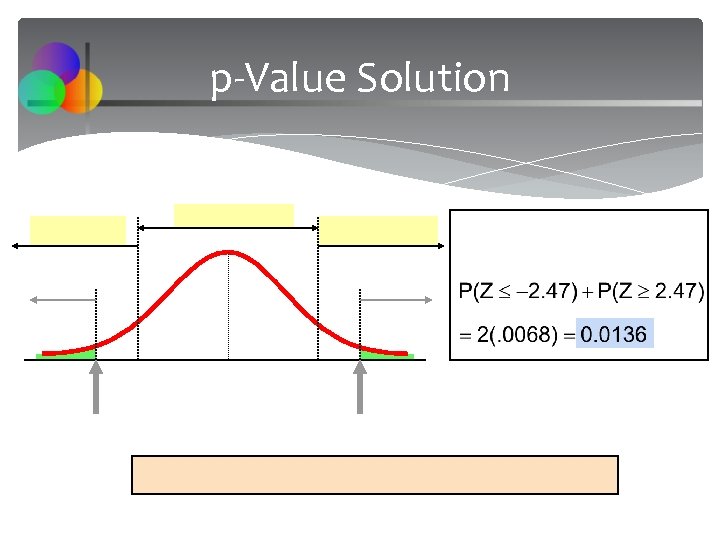 p-Value Solution
p-Value Solution
 Power of the Test Power = 1 – β = the probability that a false null hypothesis is rejected Chap 10 -43
Power of the Test Power = 1 – β = the probability that a false null hypothesis is rejected Chap 10 -43
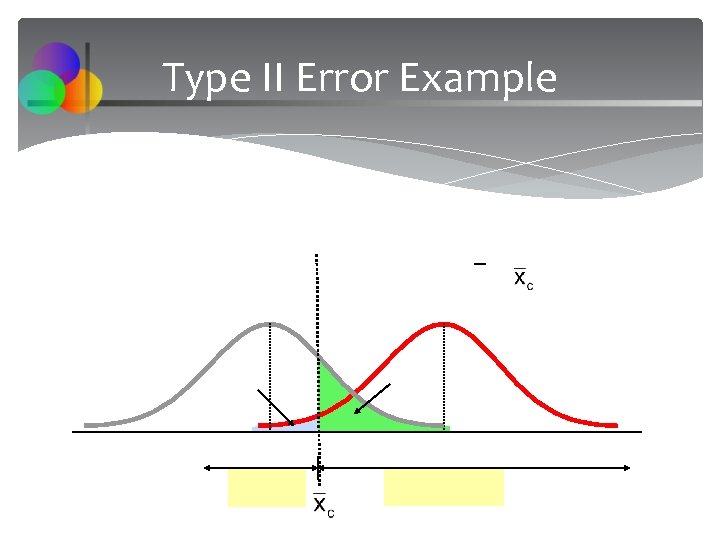
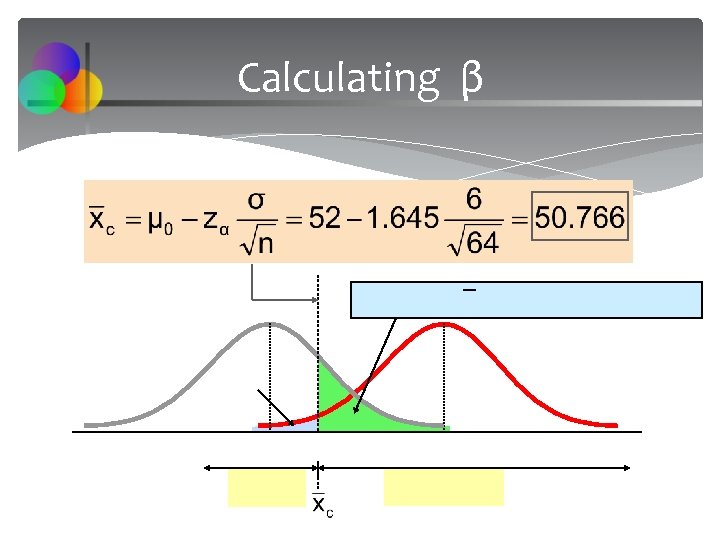
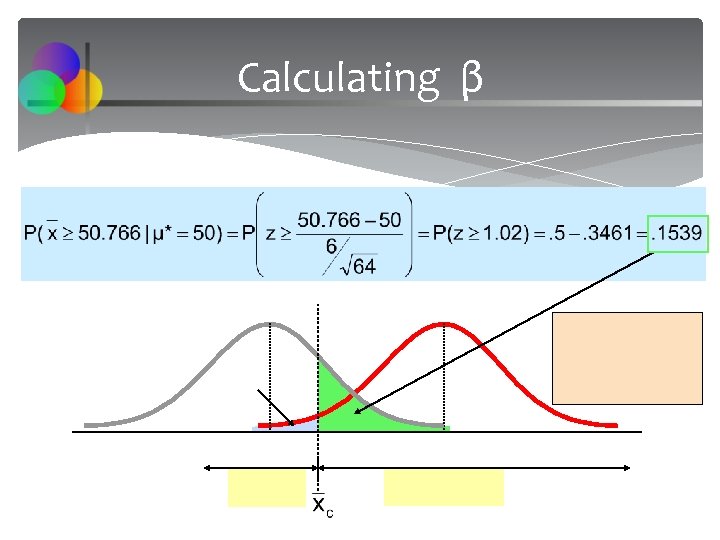
 Type II Error Assume the population is normal and the population variance is known. Consider the test The decision rule is: or If the null hypothesis is false and the true mean is μ*, then the probability of type II error is Chap 10 -44
Type II Error Assume the population is normal and the population variance is known. Consider the test The decision rule is: or If the null hypothesis is false and the true mean is μ*, then the probability of type II error is Chap 10 -44
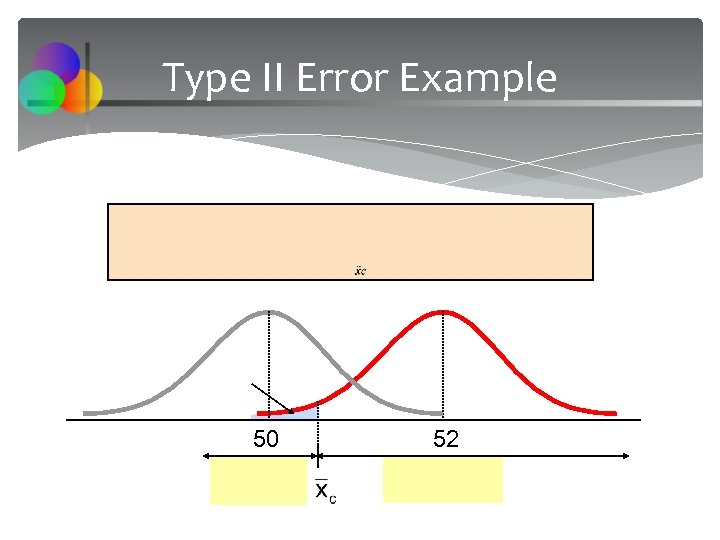 Type II Error Example 50 52
Type II Error Example 50 52
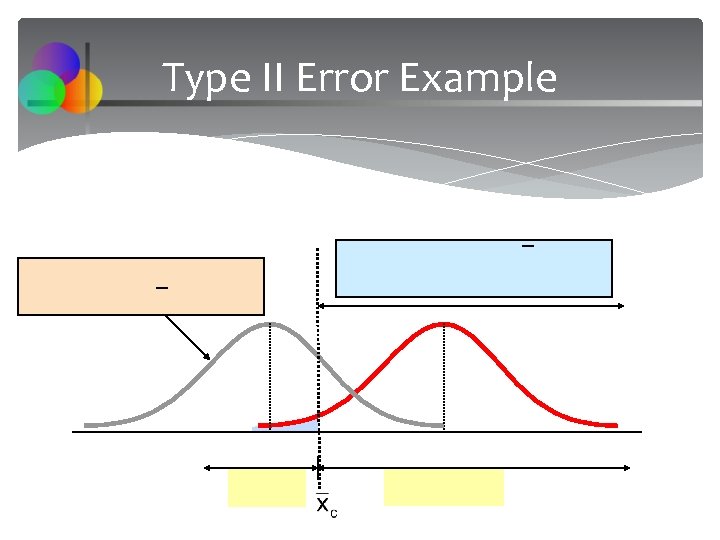 Type II Error Example
Type II Error Example
 Type II Error Example
Type II Error Example
 Calculating β
Calculating β
 Calculating β
Calculating β
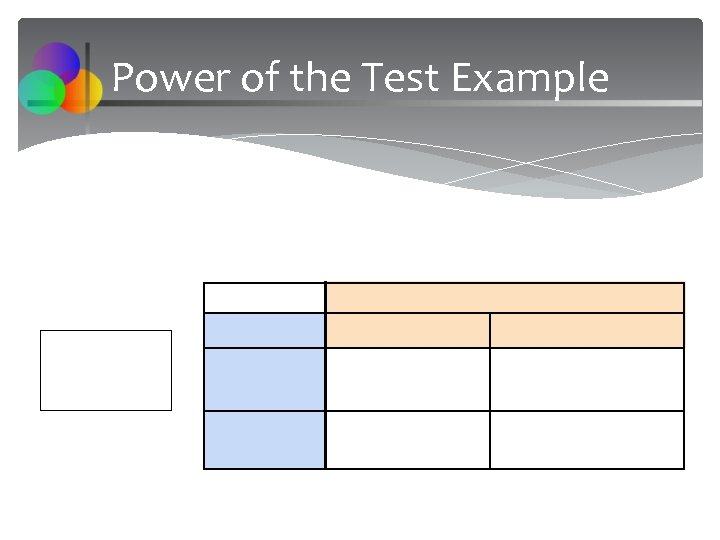 Power of the Test Example
Power of the Test Example