a4f850f9f5f0ac2990ee9e5d638c859a.ppt
- Количество слайдов: 49
 Chapter 1 The Phases of Software Development
Chapter 1 The Phases of Software Development
 Software Development Phases ● ● ● ● Specification of the task Design of a solution Implementation of solution Analysis of solution Testing and debugging Maintenance and evolution of the system Obsolescence
Software Development Phases ● ● ● ● Specification of the task Design of a solution Implementation of solution Analysis of solution Testing and debugging Maintenance and evolution of the system Obsolescence
 Specification ● ● Precise description of problem May be one of the most difficult phases
Specification ● ● Precise description of problem May be one of the most difficult phases
 Design ● Algorithm – set of instructions for solving problem ● Not originally done in programming language –pseudocode –Formal ● modeling language (UML) Decompose problem into smaller – more manageable subtasks – map to subprograms –Need to be as independent of each other as possible ● Reuse ● Modification –All domain information should be located only 1 place in the code ● Each subprogram should only do 1 task –Each subprogram should be treated as a black box – specification not implementation – called procedural abstraction / information hiding
Design ● Algorithm – set of instructions for solving problem ● Not originally done in programming language –pseudocode –Formal ● modeling language (UML) Decompose problem into smaller – more manageable subtasks – map to subprograms –Need to be as independent of each other as possible ● Reuse ● Modification –All domain information should be located only 1 place in the code ● Each subprogram should only do 1 task –Each subprogram should be treated as a black box – specification not implementation – called procedural abstraction / information hiding
 Preconditions and Postconditions An important topic: preconditions and postconditions. They are a method of specifying what a function accomplishes. Data Structures and Other Objects Using C++
Preconditions and Postconditions An important topic: preconditions and postconditions. They are a method of specifying what a function accomplishes. Data Structures and Other Objects Using C++
 Preconditions and Postconditions Frequently a programmer must communicate precisely what a function accomplishes, without any indication of how the function does its work. Can you think of a situation where this would occur ?
Preconditions and Postconditions Frequently a programmer must communicate precisely what a function accomplishes, without any indication of how the function does its work. Can you think of a situation where this would occur ?
 Example You are the head of a programming team and you want one of your programmers to write a function for part of a project. HERE ARE THE REQUIREMENTS FOR A FUNCTION THAT I WANT YOU TO WRITE. I DON'T CARE WHAT METHOD THE FUNCTION USES, AS LONG AS THESE REQUIREMENTS ARE MET.
Example You are the head of a programming team and you want one of your programmers to write a function for part of a project. HERE ARE THE REQUIREMENTS FOR A FUNCTION THAT I WANT YOU TO WRITE. I DON'T CARE WHAT METHOD THE FUNCTION USES, AS LONG AS THESE REQUIREMENTS ARE MET.
 What are Preconditions and Postconditions? One way to specify such requirements is with a pair of statements about the function. The precondition statement indicates what must be true before the function is called. The postcondition statement indicates what will be true when the function finishes its work.
What are Preconditions and Postconditions? One way to specify such requirements is with a pair of statements about the function. The precondition statement indicates what must be true before the function is called. The postcondition statement indicates what will be true when the function finishes its work.
 Example void write_sqrt(double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. .
Example void write_sqrt(double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. .
 Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. The precondition and postcondition appear as comments in your program. . }
Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. The precondition and postcondition appear as comments in your program. . }
 Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. In this example, the precondition requires that x >= 0 be true whenever the function is called. . }
Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. In this example, the precondition requires that x >= 0 be true whenever the function is called. . }
 Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 );
Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 );
 Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 ); The second and third calls are fine, since the argument is greater than or equal to zero.
Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 ); The second and third calls are fine, since the argument is greater than or equal to zero.
 Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 ); But the first call violates the precondition, since the argument is less than zero.
Example Which of these function calls meet the precondition ? write_sqrt( -10 ); write_sqrt( 5. 6 ); But the first call violates the precondition, since the argument is less than zero.
 Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. The postcondition always indicates what work the function has accomplished. In this case, when the function returns the square root of x has been written. . }
Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. The postcondition always indicates what work the function has accomplished. In this case, when the function returns the square root of x has been written. . }
 Another Example bool is_vowel( char letter ) // Precondition: letter is an uppercase or // lowercase letter (in the range 'A'. . . 'Z' or 'a'. . . 'z'). // Postcondition: The value returned by the // function is true if Letter is a vowel; // otherwise the value returned by the function is // false. .
Another Example bool is_vowel( char letter ) // Precondition: letter is an uppercase or // lowercase letter (in the range 'A'. . . 'Z' or 'a'. . . 'z'). // Postcondition: The value returned by the // function is true if Letter is a vowel; // otherwise the value returned by the function is // false. .
 Another Example What values will be returned by these function calls ? is_vowel( 'A' ); is_vowel(' Z' ); is_vowel( '? ' );
Another Example What values will be returned by these function calls ? is_vowel( 'A' ); is_vowel(' Z' ); is_vowel( '? ' );
 Another Example What values will be returned by these function calls ? is_vowel( 'A' ); is_vowel(' Z' ); is_vowel( '? ' ); true false Nobody knows, because the precondition has been violated.
Another Example What values will be returned by these function calls ? is_vowel( 'A' ); is_vowel(' Z' ); is_vowel( '? ' ); true false Nobody knows, because the precondition has been violated.
 Another Example What values will be returned by these function calls ? is_vowel( '? ' ); Violating the precondition might even crash the computer.
Another Example What values will be returned by these function calls ? is_vowel( '? ' ); Violating the precondition might even crash the computer.
 Always make sure the precondition is valid. . . The programmer who calls the function is responsible for ensuring that the precondition is valid when the function is called. AT THIS POINT, MY PROGRAM CALLS YOUR FUNCTION, AND I MAKE SURE THAT THE PRECONDITION IS VALID.
Always make sure the precondition is valid. . . The programmer who calls the function is responsible for ensuring that the precondition is valid when the function is called. AT THIS POINT, MY PROGRAM CALLS YOUR FUNCTION, AND I MAKE SURE THAT THE PRECONDITION IS VALID.
 . . . so the postcondition becomes true at the function’s end. The programmer who writes the function counts on the precondition being valid, and ensures that the postcondition becomes true at the function’s end. THEN MY FUNCTION WILL EXECUTE, AND WHEN IT IS DONE, THE POSTCONDITION WILL BE TRUE. I GUARANTEE IT.
. . . so the postcondition becomes true at the function’s end. The programmer who writes the function counts on the precondition being valid, and ensures that the postcondition becomes true at the function’s end. THEN MY FUNCTION WILL EXECUTE, AND WHEN IT IS DONE, THE POSTCONDITION WILL BE TRUE. I GUARANTEE IT.
 A Quiz Suppose that you call a function, and you neglect to make sure that the precondition is valid. Who is responsible if this inadvertently causes a 40 day flood or other disaster? You The programmer who wrote that torrential function Noah
A Quiz Suppose that you call a function, and you neglect to make sure that the precondition is valid. Who is responsible if this inadvertently causes a 40 day flood or other disaster? You The programmer who wrote that torrential function Noah
 A Quiz Suppose that you call a function, and you neglect to make sure that the precondition is valid. Who is responsible if this inadvertently causes a 40 day flood or other disaster? You The programmer who calls a function is responsible for ensuring that the precondition is valid.
A Quiz Suppose that you call a function, and you neglect to make sure that the precondition is valid. Who is responsible if this inadvertently causes a 40 day flood or other disaster? You The programmer who calls a function is responsible for ensuring that the precondition is valid.
 On the other hand, careful programmers also follow these rules: When you write a function, you should make every effort to detect when a precondition has been violated. If you detect that a precondition has been violated, then print an error message and halt the program.
On the other hand, careful programmers also follow these rules: When you write a function, you should make every effort to detect when a precondition has been violated. If you detect that a precondition has been violated, then print an error message and halt the program.
 On the other hand, careful programmers also follow these rules: When you write a function, you should make every effort to detect when a precondition has been violated. If you detect that a precondition has been violated, then print an error message and halt the program. . . . rather than causing a disaster.
On the other hand, careful programmers also follow these rules: When you write a function, you should make every effort to detect when a precondition has been violated. If you detect that a precondition has been violated, then print an error message and halt the program. . . . rather than causing a disaster.
 Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. { assert(x >= 0); . . . The assert function (described in Section 1. 1) is useful for detecting violations of a precondition.
Example void write_sqrt( double x) // Precondition: x >= 0. // Postcondition: The square root of x has // been written to the standard output. { assert(x >= 0); . . . The assert function (described in Section 1. 1) is useful for detecting violations of a precondition.
 Advantages of Using Preconditions and Postconditions Succinctly describes the behavior of a function. . . . without cluttering up your thinking with details of how the function works. At a later point, you may reimplement the function in a new way. . . . but programs (which only depend on the precondition/postcondition) will still work with no changes.
Advantages of Using Preconditions and Postconditions Succinctly describes the behavior of a function. . . . without cluttering up your thinking with details of how the function works. At a later point, you may reimplement the function in a new way. . . . but programs (which only depend on the precondition/postcondition) will still work with no changes.
 Summary Precondition The programmer who calls a function ensures that the precondition is valid. The programmer who writes a function can bank on the precondition being true when the function begins execution. Postcondition The programmer who writes a function ensures that the postcondition is true when the function finishes executing.
Summary Precondition The programmer who calls a function ensures that the precondition is valid. The programmer who writes a function can bank on the precondition being true when the function begins execution. Postcondition The programmer who writes a function ensures that the postcondition is true when the function finishes executing.
 C++ Features: Standard Library & Standard Namespace ● #include directive –Similar –Much ● ● ● to import directive in other languages more primitive Namespaces – allows limiting visibility of “names” Standard namespace – standard C++ libraries 2 choices –using namespace std: –Fully qualified identifier
C++ Features: Standard Library & Standard Namespace ● #include directive –Similar –Much ● ● ● to import directive in other languages more primitive Namespaces – allows limiting visibility of “names” Standard namespace – standard C++ libraries 2 choices –using namespace std: –Fully qualified identifier
 Exception Handling ● Similar to Java and C#
Exception Handling ● Similar to Java and C#
 Running Time Analysis ● ● Machine independent method of measuring run time efficiency Determine basic operation for the algorithm Expression the number of operations as a function of the data size Interested in the order of magnitude of this function – expressed using Big-O notation
Running Time Analysis ● ● Machine independent method of measuring run time efficiency Determine basic operation for the algorithm Expression the number of operations as a function of the data size Interested in the order of magnitude of this function – expressed using Big-O notation
 Running Time Analysis ● ● ● Worst case – maximum number of operations Best case – minimum number of operations Average case – depends upon the underlying probability distribution
Running Time Analysis ● ● ● Worst case – maximum number of operations Best case – minimum number of operations Average case – depends upon the underlying probability distribution
 The Big-O Notation Analyze algorithm after design Example 50 packages delivered to 50 different houses 50 houses one mile apart, in the same area FIGURE 1 -1 Gift shop and each dot representing a house
The Big-O Notation Analyze algorithm after design Example 50 packages delivered to 50 different houses 50 houses one mile apart, in the same area FIGURE 1 -1 Gift shop and each dot representing a house
 The Big-O Notation Example (cont’d. ) Driver picks up all 50 packages Drives one mile to first house, delivers first package Drives another mile, delivers second package Drives another mile, delivers third package, and so on Distance driven to deliver packages 1+1+1+… +1 = 50 miles Total distance traveled: 50 + 50 = 100 miles FIGURE 1 -2 Package delivering scheme
The Big-O Notation Example (cont’d. ) Driver picks up all 50 packages Drives one mile to first house, delivers first package Drives another mile, delivers second package Drives another mile, delivers third package, and so on Distance driven to deliver packages 1+1+1+… +1 = 50 miles Total distance traveled: 50 + 50 = 100 miles FIGURE 1 -2 Package delivering scheme
 The Big-O Notation Example (cont’d. ) Similar route to deliver another set of 50 packages Driver picks up first package, drives one mile to the first house, delivers package, returns to the shop Driver picks up second package, drives two miles, delivers second package, returns to the shop Total distance traveled 2 * (1+2+3+…+50) = 2550 miles FIGURE 1 -3 Another package delivery scheme
The Big-O Notation Example (cont’d. ) Similar route to deliver another set of 50 packages Driver picks up first package, drives one mile to the first house, delivers package, returns to the shop Driver picks up second package, drives two miles, delivers second package, returns to the shop Total distance traveled 2 * (1+2+3+…+50) = 2550 miles FIGURE 1 -3 Another package delivery scheme
 The Big-O Notation Example (cont’d. ) n packages to deliver to n houses, each one mile apart First scheme: total distance traveled 1+1+1+… +n = 2 n miles Function of n Second scheme: total distance traveled 2 * (1+2+3+…+n) = 2*(n(n+1) / 2) = n 2+n Function of n 2
The Big-O Notation Example (cont’d. ) n packages to deliver to n houses, each one mile apart First scheme: total distance traveled 1+1+1+… +n = 2 n miles Function of n Second scheme: total distance traveled 2 * (1+2+3+…+n) = 2*(n(n+1) / 2) = n 2+n Function of n 2
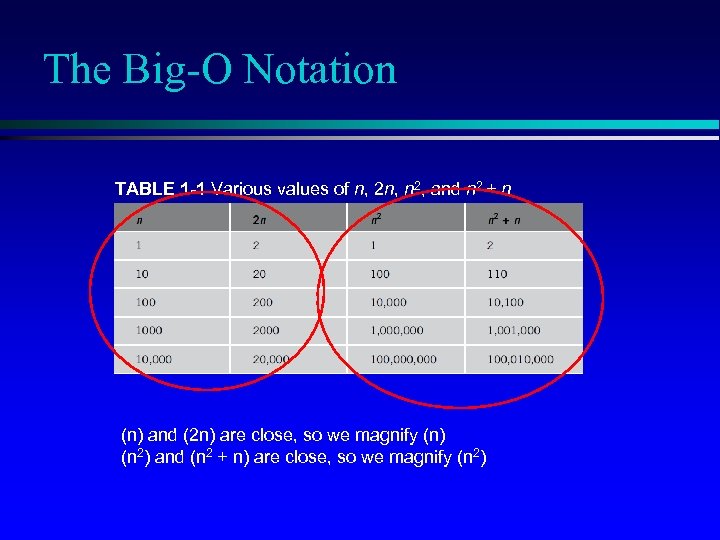 The Big-O Notation TABLE 1 -1 Various values of n, 2 n, n 2, and n 2 + n (n) and (2 n) are close, so we magnify (n) (n 2) and (n 2 + n) are close, so we magnify (n 2)
The Big-O Notation TABLE 1 -1 Various values of n, 2 n, n 2, and n 2 + n (n) and (2 n) are close, so we magnify (n) (n 2) and (n 2 + n) are close, so we magnify (n 2)
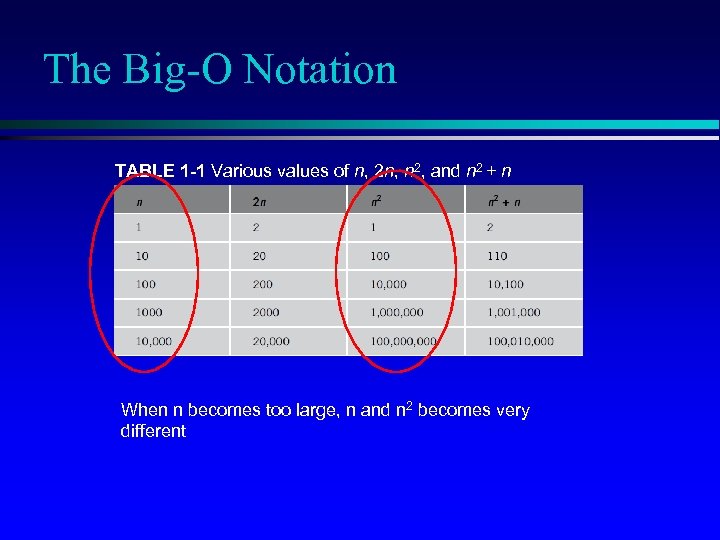 The Big-O Notation TABLE 1 -1 Various values of n, 2 n, n 2, and n 2 + n When n becomes too large, n and n 2 becomes very different
The Big-O Notation TABLE 1 -1 Various values of n, 2 n, n 2, and n 2 + n When n becomes too large, n and n 2 becomes very different
 The Big-O Notation Analyzing an algorithm Count number of operations performed Not affected by computer speed
The Big-O Notation Analyzing an algorithm Count number of operations performed Not affected by computer speed
 The Big-O Notation Example 1 -1 Illustrates fixed number of executed operations 1 operation Only one of them will be executed 2 operations 1 operation 3 operations
The Big-O Notation Example 1 -1 Illustrates fixed number of executed operations 1 operation Only one of them will be executed 2 operations 1 operation 3 operations
 The Big-O Notation Example 1 -2 Illustrates dominant operations N times the condition is TRUE + 1 time the condition is FALSE 2 operations 1 operation N+1 operations Executed while the cond. is TRUE 2 N operations 3 operations Only one of them will be executed, take the max: 2 1 operation 2 operations 1 operation 3 operation If the while loop executes N times then: 2+1+1+1+5*N + 1 + 3 + 1 + 2 + 3 = 5 N+15
The Big-O Notation Example 1 -2 Illustrates dominant operations N times the condition is TRUE + 1 time the condition is FALSE 2 operations 1 operation N+1 operations Executed while the cond. is TRUE 2 N operations 3 operations Only one of them will be executed, take the max: 2 1 operation 2 operations 1 operation 3 operation If the while loop executes N times then: 2+1+1+1+5*N + 1 + 3 + 1 + 2 + 3 = 5 N+15
 The Big-O Notation How to count for loops 1 op Times the cond. Is TRUE + 1 (when the condition is FALSE for (initialization; condition; increase){ statement 1; Times the cond. statement 2; Is TRUE. . . }
The Big-O Notation How to count for loops 1 op Times the cond. Is TRUE + 1 (when the condition is FALSE for (initialization; condition; increase){ statement 1; Times the cond. statement 2; Is TRUE. . . }
 Example 1 op 6 op 5 op for(i=1; i<=5; i++) 5 op 30 op 25 op for(j=1; j<=5; j++) { 25 op cout <<“*”; sum =sum+j; } 25 op Finally: 147 25 op for(i=1; i<=n; i++) for(j=1; j<=n; j++){ cout <<“*”; Sum=sum + j; } 2 n+2+ 2 n 2+2 n+ 3 n 2 = 5 n 2+ 4 n+2
Example 1 op 6 op 5 op for(i=1; i<=5; i++) 5 op 30 op 25 op for(j=1; j<=5; j++) { 25 op cout <<“*”; sum =sum+j; } 25 op Finally: 147 25 op for(i=1; i<=n; i++) for(j=1; j<=n; j++){ cout <<“*”; Sum=sum + j; } 2 n+2+ 2 n 2+2 n+ 3 n 2 = 5 n 2+ 4 n+2
 The Big-O Notation TABLE 1 -2 Growth rates of various functions
The Big-O Notation TABLE 1 -2 Growth rates of various functions
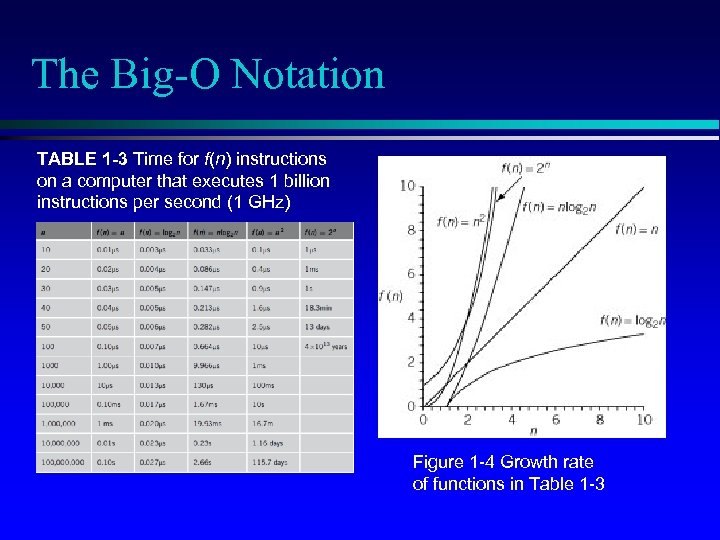 The Big-O Notation TABLE 1 -3 Time for f(n) instructions on a computer that executes 1 billion instructions per second (1 GHz) Figure 1 -4 Growth rate of functions in Table 1 -3
The Big-O Notation TABLE 1 -3 Time for f(n) instructions on a computer that executes 1 billion instructions per second (1 GHz) Figure 1 -4 Growth rate of functions in Table 1 -3
 The Big-O Notation As n becomes larger and larger Term 4 n + 20 in f(n) becomes insignificant Term n 2 becomes dominant term TABLE 1 -4 Growth rate of n 2 and n 2 + 4 n + 20 n
The Big-O Notation As n becomes larger and larger Term 4 n + 20 in f(n) becomes insignificant Term n 2 becomes dominant term TABLE 1 -4 Growth rate of n 2 and n 2 + 4 n + 20 n
 The Big-O Notation Algorithm analysis If function complexity can be described by complexity of a quadratic function without the linear term We say the function is of O(n 2) or Big-O of n 2 Let f and g be real-valued functions Assume f and g nonnegative For all real numbers n, f(n) >= 0 and g(n) >= 0 f(n) is Big-O of g(n): written f(n) = O(g(n)) If there exists positive constants c and n 0 such that f(n) <= cg(n) for all n >= n 0
The Big-O Notation Algorithm analysis If function complexity can be described by complexity of a quadratic function without the linear term We say the function is of O(n 2) or Big-O of n 2 Let f and g be real-valued functions Assume f and g nonnegative For all real numbers n, f(n) >= 0 and g(n) >= 0 f(n) is Big-O of g(n): written f(n) = O(g(n)) If there exists positive constants c and n 0 such that f(n) <= cg(n) for all n >= n 0
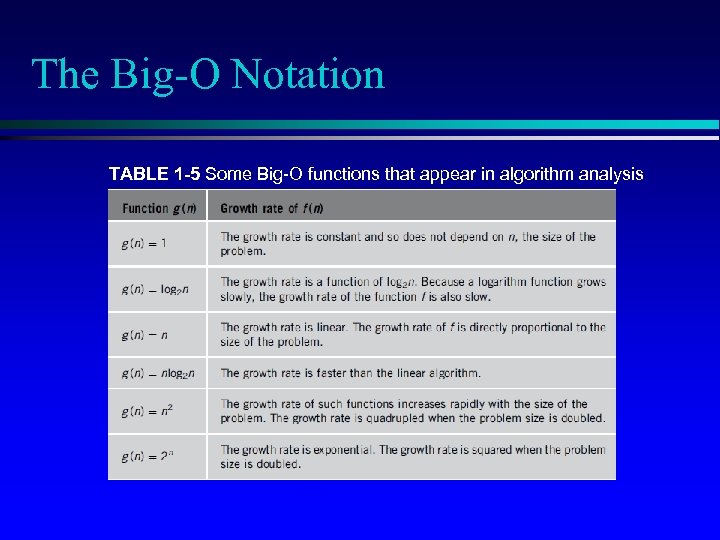 The Big-O Notation TABLE 1 -5 Some Big-O functions that appear in algorithm analysis
The Big-O Notation TABLE 1 -5 Some Big-O functions that appear in algorithm analysis
 Testing and Debugging ● Good test data –Correct output known –Include values most likely to causes errors Boundary values ● –Fully exercise code Every line of code is executed by at least 1 test case ●
Testing and Debugging ● Good test data –Correct output known –Include values most likely to causes errors Boundary values ● –Fully exercise code Every line of code is executed by at least 1 test case ●
