Chapter 1 Mc Graw-Hill Irwin A Brief History of

Learning Objectives • How to calculate the return on an investment using different methods. • The historical returns on various important types of investments. • The historical risk on various important types of investments. • The relationship between risk and return. 1 -2

A Brief History of Risk and Return • Our goal in this chapter is to see what financial market history can tell us about risk and return. • There are two key observations: – First, there is a substantial reward, on average, for bearing risk. – Second, greater risks accompany greater returns. • These observations are important investment guidelines. 1 -3

Dollar Returns • Total dollar return is the return on an investment measured in dollars, accounting for all interim cash flows and capital gains or losses. • The gain or (loss) you get if you buy an asset is called the return on an investment. • Return on investment has two components: 1. cash received while owning the investment (dividends) 2. The change in the value of the asset(stock) will be either a capital gain or a capital loss of your investment. 1 -4

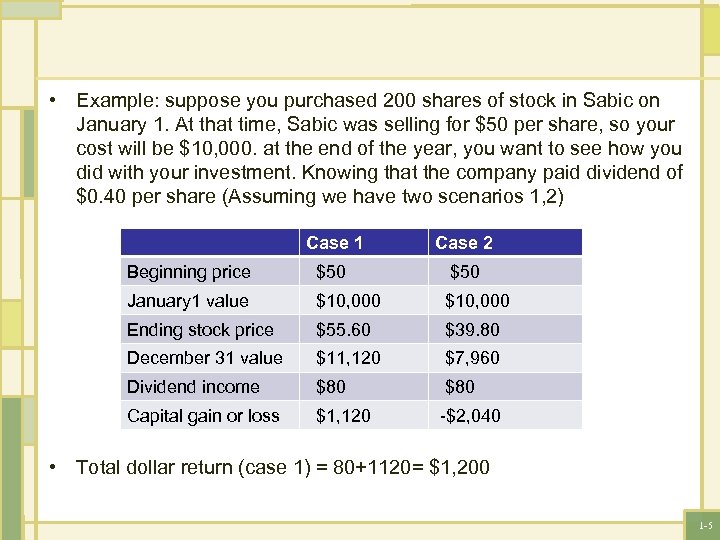
• Example: suppose you purchased 200 shares of stock in Sabic on January 1. At that time, Sabic was selling for $50 per share, so your cost will be $10, 000. at the end of the year, you want to see how you did with your investment. Knowing that the company paid dividend of $0. 40 per share (Assuming we have two scenarios 1, 2) Case 1 Case 2 Beginning price $50 January 1 value $10, 000 Ending stock price $55. 60 $39. 80 December 31 value $11, 120 $7, 960 Dividend income $80 Capital gain or loss $1, 120 -$2, 040 • Total dollar return (case 1) = 80+1120= $1, 200 1 -5

Percent Returns • Total percent return is the return on an investment measured as a percentage of the original investment. • The total percent return is the return for each dollar invested. • Dividend Yield: The annual stock dividend as a percentage of the initial stock price. ( D /pt) Capital gain yield: the change in stock price as a percentage of the initial stock price (Pt+1 – Pt / Pt) • 1 -6

Example: Calculating Total Dollar and Total Percent Returns • • • Suppose you invested $1, 400 in a stock with a share price of $35. After one year, the stock price per share is $49. Also, for each share, you received a $1. 40 dividend. • What was your total dollar return? – – • $1, 400 / $35 = 40 shares Capital gain: 40 shares times $14 = $560 Dividends: 40 shares times $1. 40 = $56 Total Dollar Return is $560 + $56 = $616 What was your total percent return? – Dividend yield = $1. 40 / $35 = 4% – Capital gain yield = ($49 – $35) / $35 = 40% – Total percentage return = 4% + 40% = 44% Note that $616 divided by $1, 400 is 44%. 1 -7

Annualizing Returns, I • You buy 200 shares of Lowe’s Companies, Inc. at $18 per share. Three months later, you sell these shares for $19 per share. You received no dividends. What is your return? What is your annualized return? • Return: (Pt+1 – Pt) / Pt = ($19 - $18) / $18 =. 0556 = 5. 56% This return is known as the holding period percentage return. • Effective Annual Return (EAR): The return on an investment expressed on an “annualized” basis. Key Question: What is the number of holding periods in a year? 1 -8

Annualizing Returns, II 1 + EAR = (1 + holding period percentage return)m m = the number of holding periods in a year. • In this example, m = 4 (12 months / 3 months). Therefore: 1 + EAR = (1 +. 0556)4 = 1. 2416. So, EAR =. 2416 or 24. 16%. 1 -9

The Historical Record We will examine different categories of financial investments(portfolios) from 1929 to 2009 : 1. Large company stock “large cap”: contains largest companies in terms of market value of outstanding stocks. 2. Small company stock “mall cap” 3. Long term government bonds (20 years to maturity) 4. Treasury bills (three months to maturity) 1 -10

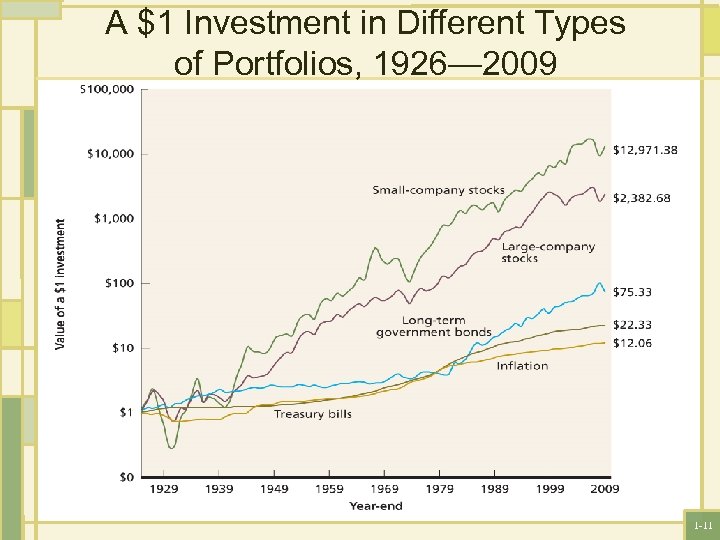
A $1 Investment in Different Types of Portfolios, 1926— 2009 1 -11

Historical Average Returns • Using the data in Table 1. 1, if you add up the returns for large-company stocks from 1926 through 2009, you get about 987 percent. • Because there are 84 returns, the average return is about 11. 75%. How do you use this number? • If you are making a guess about the size of the return for a year selected at random, your best guess is 11. 75%. • The formula for the historical average return is: 1 -12

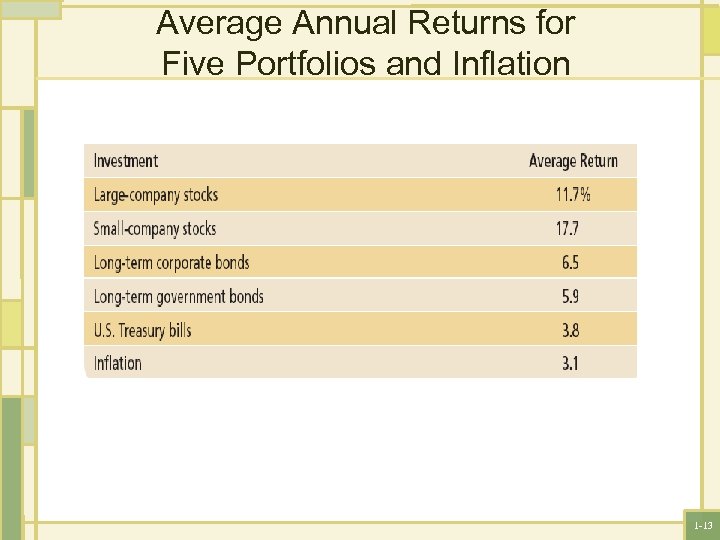
Average Annual Returns for Five Portfolios and Inflation 1 -13

Average Returns: The First Lesson • Risk-free rate: The rate of return on a riskless certain investment. (Treasury bills) • Risk premium: The extra return on a risky asset over the risk-free rate; or the reward for bearing risk. • The First Lesson: There is a reward, on average, for bearing risk. The Second Lesson: The greater the potential reward, the greater the risk. 1 -14

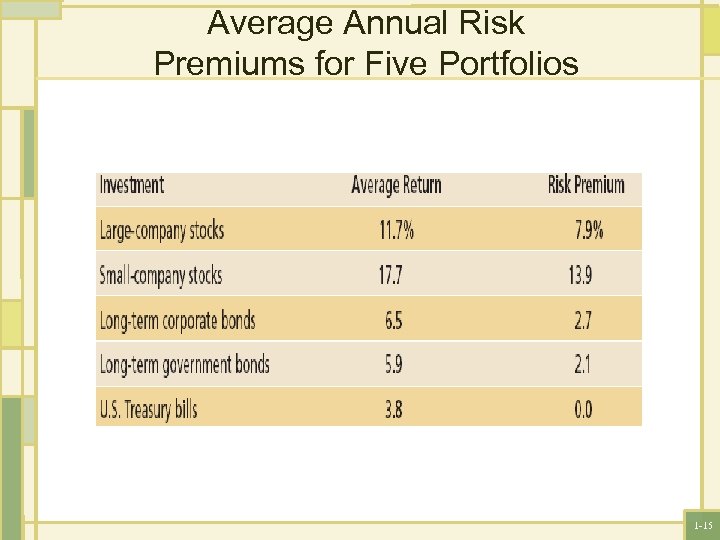
Average Annual Risk Premiums for Five Portfolios 1 -15

Return Variability Review and Concepts • Variance is a common measure of return dispersion. Sometimes, return dispersion is also call variability. • To know how much the actual return differs from the average return in a typical year. • Standard deviation is the square root of the variance. The square root of the variance is used because the variance is measured in squared percentages and thus its hard to interpret. However, the standard deviation is an ordinary percentage. . 1 -16

Return Variability: The Statistical Tools • The formula for return variance is ("n" is the number of returns): • Sometimes, it is useful to use the standard deviation, which is related to variance like this: • Check the example on page 20. 1 -17

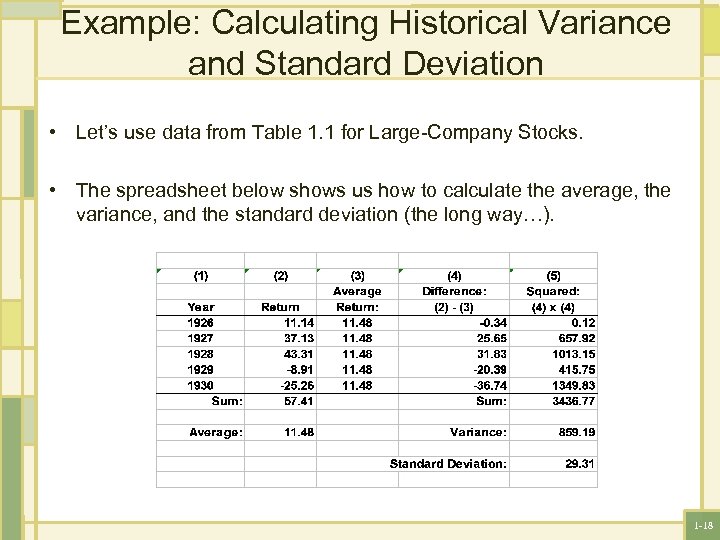
Example: Calculating Historical Variance and Standard Deviation • Let’s use data from Table 1. 1 for Large-Company Stocks. • The spreadsheet below shows us how to calculate the average, the variance, and the standard deviation (the long way…). 1 -18

• Normal distribution: A symmetric, bell-shaped frequency distribution that can be described with only an average and a standard deviation. • It is useful for describing the probability of ending up in a given range of return. • The probability that we end up within one SD of the average is 68%. (the average# +or – 1 SD) • The probability that we end up within two SD of the average is 95% (the average # = or – 2 SD) • The probability that we end up with more three SD of the average is 1% (the average# + or – 3 SD) 1 -19

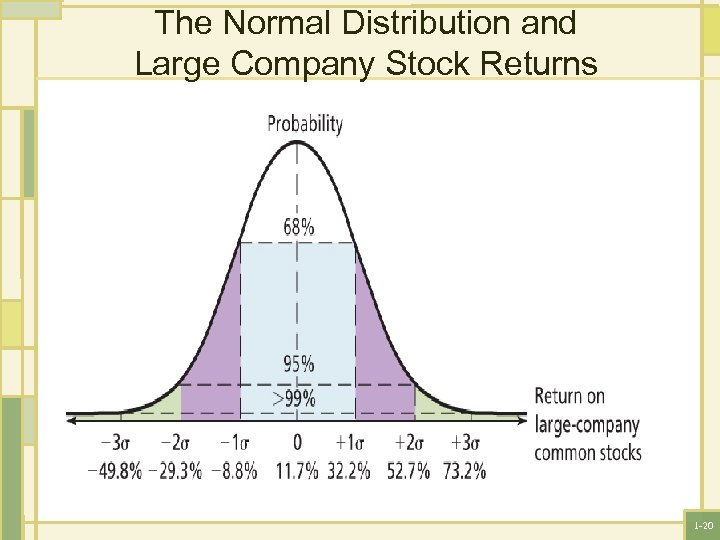
The Normal Distribution and Large Company Stock Returns 1 -20

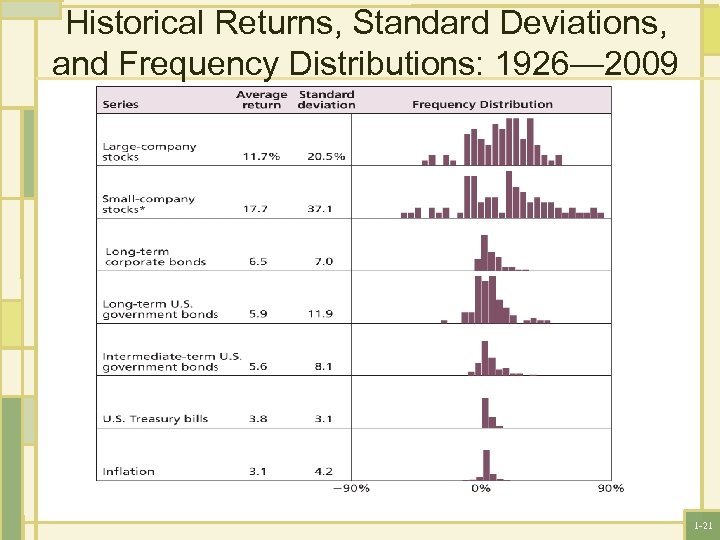
Historical Returns, Standard Deviations, and Frequency Distributions: 1926— 2009 1 -21

RISK & RETURN • If the investor is unwilling to bear any risk but is willing to forgo the use of money for a while, then they can invest in a risk free rat asset. • If the investor is willing to bear the risk , then they should accept risk premiums when investing in risky assets. NOTE Risky investment do not always pay more than risk free investments (that’s what makes them risky). In other words, there is a risk premium on average but over any particular time, there is no guarantee. 1 -22

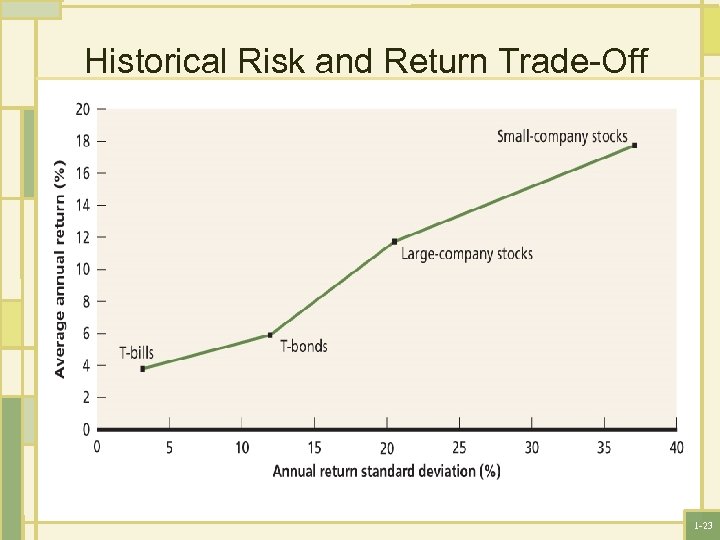
Historical Risk and Return Trade-Off 1 -23