Chapter 1 Introduction 1 1 1 Introduction

Chapter 1 Introduction 1

1. 1 Introduction q Networks: mathematical models of real systems like electrical and power/ telecom/ logistics/ highway/ rail/ airline/ water, etc. q Also network models frequently show up for problems that look irrelevant to physical networks. Important modeling/algorithmic tool. q Graph, Network: G = (N, A) ( G = (V, E) ) Ø N: set of nodes, usually |N| = n Ø A: set of arcs, |A| = m • (i, j) A, {i}, {j} N (ordered/unordered pair of distinct nodes) (directed network/undirected network, graph) Ø V: vertex set Ø E: edge set Ø parallel arcs, loops may be considered, but no hyper graph Network Theory and Applications 2010 2

q Two major categories: flow networks, topological graph theory q Many flow network problems can be modeled as LP. Ø Interpret the behavior of LP algorithms on network problems. Ø Emphasis on specialized algorithms for network problems. Ø Special attention on running times of algorithms(polynomial solvability, efficient algorithm) Ø Implementation issues, data structures q Basic problems to consider Ø Shortest path problem Ø Maximum flow problem Ø Minimum cost flow problem Network Theory and Applications 2010 3

1. 2 Network Flow Problems q Minimum cost flow problem Given directed G = (N, A) For each arc (i, j) A, cost cij , capacity uij, lower bound lij (usually 0) For each node i N, supply demand b(i) Ø b(i) > 0: supply node Ø b(i) < 0: demand node Ø b(i) = 0: transshipment node decision variables: xij amount of flow on arc (i, j) A q Want minimum cost flows that satisfy supply/demand at every node and arc capacity constraints on the arcs. q Quite general problem. Has many problems as special cases Network Theory and Applications 2010 4

q Formulation Minimize subject to (i, j) A cij xij {j: (i, j) A} xij - {j: (j, i) A} xji = b(i) for all i N, lij xij uij for all (i, j) A, q Matrix notation Minimize cx subject to Nx = b, l x u, N: (1. 1 b) (1. 1 c) (1. 2 b) (1. 2 c) n m matrix, called node-arc incidence matrix the column Nij corresponds to the variable xij column Nij has a +1 in the i-th row, a -1 in the j-th row; others are 0. necessary condition for feasibility is i=1 n b(i) = 0 (add the left hand side and right hand side of (1. 1 b) respectively, have 0 x = b(i) ) Network Theory and Applications 2010 5

Minimize subject to (i, j) A cij xij {j: (i, j) A} xij - {j: (j, i) A} xji = b(i) for all i N, lij xij uij for all (i, j) A, (1. 1 b) (1. 1 c) (1. 1 b) called mass balance constraints or flow conservation constraints ( outflow – inflow = net flow at node i) (1. 1 c) called flow bound constraints q Assume all data are integral (integrality assumption) Otherwise, multiply suitably large integer to rational numbers to convert them to integers. q If all data integral, optimal solution is integer valued (later). Network Theory and Applications 2010 6

q Shortest path problem Given directed G = (N, A), arc cost (length) cij for (i, j) A. Find a minimum cost (or length) path from a specified source node s to another specified sink node t. q Transformation to MCF: Let b(s) = 1, b(t) = -1, others 0, arc capacities 1 (or 1). q Variations Ø All pairs shortest path Ø k-shortest path (enumeration) Ø Longest path (quite different, NPC) q Be careful about the conditions on data Ø cij 0 (easy) Ø cij < 0 allowed, but no negative cycle (takes more time, but still polynomial time algorithms exist) Ø cij < 0 allowed, negative cycle exists (difficult, NPC) Network Theory and Applications 2010 7

q Maximum flow problem Given: G = (N, A), arc capacities uij 0, (i, j) A, specified source node s, sink node t Find maximum flow that can be sent from source node s to sink node t. q Transformation to MCF: Let b(i) = 0, for all i N, cij = 0, for all (i, j) A Add arc from t to s, with capacity and cost = -1 q Maximum flow problem is related to minimum cut problem. Network Theory and Applications 2010 8

q Assignment problem: G = (N, A), N = N 1 N 2, N 1 N 2 = , |N 1| = |N 2| A N 1 N 2 , cost cij for each (i, j) A Find assignments which pair each node in N 1 to a node in N 2 with minimum cost. q Transformation to MCF: Let b(i) = 1, for all i N 1 = -1, for all i N 2 uij = 1, for all (i, j) A Network Theory and Applications 2010 9

q Transportation problem: Special case of MCF N = N 1 N 2, N 1 N 2 = , N 1: supply nodes, N 2: demand nodes for each (i, j) A, i N 1, j N 2 q Ex) minimum cost distribution of goods from warehouses (N 1) to customers (N 2). Cost cij is the cost of a distribution channel from warehouse i to customer j (may involve many consecutive transportation means). Network Theory and Applications 2010 10

q Circulation problem: Minimum cost flow problem with only transshipment nodes, i. e. b(i) = 0 for all i N. lower bound (lij, may not be 0) and upper bound (uij) imposed on the flows. Find a feasible flow with minimum cost, or verify if a feasible flow exists (cij = 0) for the network. Network Theory and Applications 2010 11

q Convex cost flow problem: Cost function for flow not linear function, but convex function. (cost increases more than linear as there are more flows: congestion on arcs, . . ) How about concave cost function? (ex: fixed charge network flow problem) q Generalized flow problem: xij units of flow enter arc (i, j) ijxij units arrive at node j. 0 < ij < 1: lossy arc 1 < ij < : gainy arc ex) Ø Power transmission through electric lines Ø Flow of water through pipelines or canals Ø Transportation of perishable commodity Ø Cash management Network Theory and Applications 2010 12

q Multicommodity flow problem: Multiple commodities share the common network. Mass balance equations for each commodity. Each commodity has origins/destinations. Commodities can use the same arc together, but should observe the capacity of the arc. Ø Multiple origin/destination for each commodity Ø One origin, one destination for each commodity • Transmission network, freight train Network Theory and Applications 2010 13

q Other models Ø Minimum spanning tree problem: G = (N, A) undirected, arc weight cij for (i, j) A Spanning tree: tree (connected acyclic graph) that spans all nodes of an undirected network Find minimum cost spanning tree. Simplest form of connectedness Variations: Arborescence (directed tree), Steiner tree, capacitated tree, etc. Network Theory and Applications 2010 14

Ø Matching problem: G = (N, A), undirected Matching: set of arcs (edges) of G with the property that every node is incident to at most one arc in the set Find a matching that optimizes some criteria (min cost perfect matching, maximum cardinality matching, maximum weight matching, b-matching, …) Assignment problem bipartite matching problem (|N 1|, |N 2| may not be equal) Ex) matching roommates, matching pilots to compatible airplanes, scheduling airline crews for available flight legs, assigning duties to bus drivers, plotter scheduling… Ø Related problems: Chinese postman problem, T-joins, edge coloring, … Ø Similar looking but quite different problem: stable set (node packing) problem. stable set: set of nodes such that no two of them are joined by an edge. maximum cardinality (or weighted) stable set problem is NP-hard traveling salesman problem (compare to Chinese postman problem) is NP-hard Network Theory and Applications 2010 15

1. 3 Applications q Application 1. 1 Reallocation of Housing House categories i = 1, … , n Tenants wants to move to the house of different categories. cyclic change is desirable. Network Theory and Applications 2010 16

q Application 1. 2 Assortment of Structural Steel Beams Steel beems of varying lengths, i = 1, … , n Di > 0: demand of steel beam of length Li, L 1 < L 2 < … < Ln Can cut longer length beam and use it for shorted length (scraps result) Let Ki: cost of inventory facility for beams of length Li Ci: cost of a beam of Length Li Want to find inventory set up plan to minimize the total cost (facility cost + scrap loss) q Model: nodes 0, 1, … , n arc (i, j): represent we maintain inventory of length Lj and use them for the demand of beams of length Li+1, Li+2, … , Lj cij = Kj + Cj k=i+1 j Dk. Find shortest path from 0 to n. Network Theory and Applications 2010 17

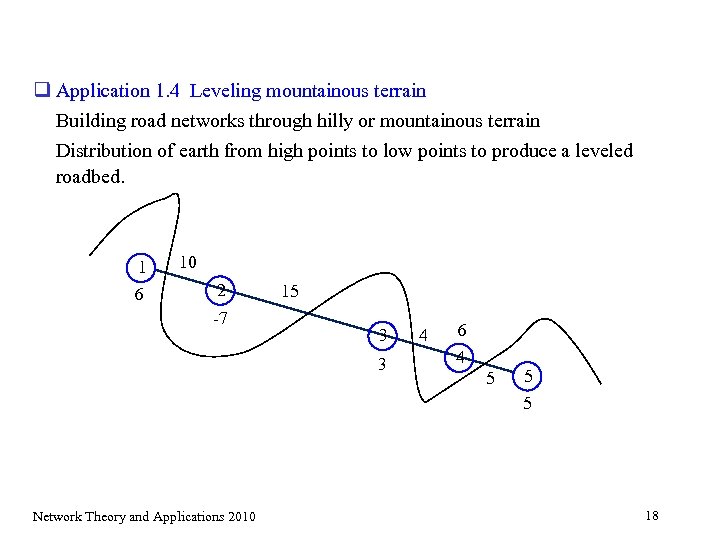q Application 1. 4 Leveling mountainous terrain Building road networks through hilly or mountainous terrain Distribution of earth from high points to low points to produce a leveled roadbed. 1 6 10 2 -7 15 3 3 4 6 4 5 5 5 Network Theory and Applications 2010 18

q Application 1. 6 Pairing stereo speakers Must pair individual speakers to sell them as a set Measure the responses of the speakers at 20 discrete frequencies matching coefficients for a pair calculated as the sum of absolute differences of responses at each frequency. q Objectives 1. Find as many pairs as possible whose matching coefficients do not exceed a specification limit 2. Pairing speakers within specification limits to minimize the total sum of the matching coefficients. Network Theory and Applications 2010 19

q Application 1. 10 Racial balancing of schools In 1968, nondiscrimination rule for school system. Need to balance the ratios between races. q S schools with capacity uj for school j. School j should have [ljk, ujk] student from the k-th ethnic group. L population centers. Sik denote the number of students of the k-th ethnic group at the i-th population center. fij: distance between population center i and school j. q Find assignment of students to schools so that the ethnic requirement for each school is satisfied and minimize the total distance traveled by the students. q Multicommodity flow problem. Network Theory and Applications 2010 20

(cost, [lower bound, upper bound]) 0, [0, Sik] i=13 Si 1 b 1 fij, [0, ] d 1 a 1 c 2 d 2 a 2 e 2 b 3 Ethnic groups (sources) 0, [ljk, ujk] e 1 - i=13 Si 1 b 2 i=13 Si 2 c 1 0, [0, uj] Population centers Network Theory and Applications 2010 c 3 Schools (input) - i=13 Si 2 d 3 Schools (output) Ethnic groups (sinks) 21