4f97bc90be1fa6f904308fa5f6a52240.ppt
- Количество слайдов: 65

Chapter 1 Collecting Data in Reasonable Ways Created by Kathy Fritz

Data and conclusions based on data are everywhere Should you believe • Newspapers what you read? • Magazines • On-line reports • Professional publications chi one hour per week Will doing tai increase the effectiveness of your flu shot? These type of questions are answered with data gathered from samples or from experiments. Will eating cheese before going Should you eat garlic to bed help you sleep better? prevent a cold?
Population – the entire collection of individuals or objects that you want to learn about Sample – the part of the population that is selected for study

In the article, “The ‘CSI Effect’ – Does It Really Exist? ” (National Institute of Justice [2008]: 1 -7), the author speculates that watching crime scene investigation TV shows may be associated with the kind of high-tech evidence that jurors expect to see in criminal trials. Do people who watch such shows on a regular basis have higher expectations than those who do not watch them? How would one go about answering this question? To answer this question, study in which select Observational study – aone would need to the a sample of people who watch these shows and person conducting the study observes a sample of people who do not. Interview these people to characteristics of a sample selected from one or determine their level of expectation of high-tech more existing evidence in criminal cases. populations. The goal of an observational study is to use data from This is called an observational study. the sample to learn about the corresponding population.
Suppose a chemistry teacher wants to see the effects on students’ test scores if the lab time were increased from 3 hours to 6 hours. Would you use an observational study to answer this question? Why or why not? Questions in the form “What would happen when. . . ? ” or “What is the effect of. . . ? ” CANNOT be answered with data from an observational study. Experiment - a study in which the person An experiment MUST be used. conducting the study looks at how a response variable behaves under different experimental conditions.

A big difference between an experiment and an observational study is. . . • in an experiment, the person carrying In the study about the “CSI effect”, the out the example determines who will be researcher did NOT determine whether or not the in what experimental groups and what people watched investigative TV shows. the experimental conditions will be • in In the example about increasingthe time in a an observational study, lab person chemistry class to see the effect on test scores, carrying would determine does NOT the teacher out the study which students are in determinelab andwill be ininwhat groups the 3 -hour who which are the 6 -hour lab.
Observational Studies • Purpose is to collect data that will allow you to learn about a single population or about how two or more populations will differ to carry out a The “ideal” study would be census. • Allows you to answer questions like “What is the proportion of. . . ? ” Obtaining information about the entire “What is the average of. . . ? ” population is called a census. “Is there an association between. . . ? ”

Census versus Sample Why might we prefer to take select a sample rather than perform a census? 1. Measurements that require destroying the item Measuring how long batteries last Safety ratings of cars 2. Difficult to find entire population Length of fish in a lake 3. Limited resources Time and money Most common reason to use a sample

When you answer questions like “What is the proportion of. . . ? ” “What is the average of. . . ? ” How can we be sure that way sample is a One the is to take representative ofthe population? You are interested in simple random sample. characteristic. It is important that a sample be A population characteristic is a number that representative of the population. describes the entire population. A statistic is a number that describes a sample.

Simple Random Sample A sample of size n is selected from the population in a way that ensures that every different possible sample of the desired size has the same is used to denoteselected. size; the The letter n chance of being sample number of individuals or objects in the sample. Suppose you want to select 10 employees from all employees of a large design firm. In order to be a simple random sample – EVERY sample each employee with a unique number. 10 is the have What MUST value of n ? create Numberof size a simple randoman equal chance to To select sample, occur. Thus, it is possible that a full-time, Use aarandom digit table random, 10 randomthe 10 list (called a sampling frame) of all part-time, or any combination of full-time and number generator, or numbers selected from a employees in the firm. part-time employees are selected. hat to select the 10 employees for the sample.
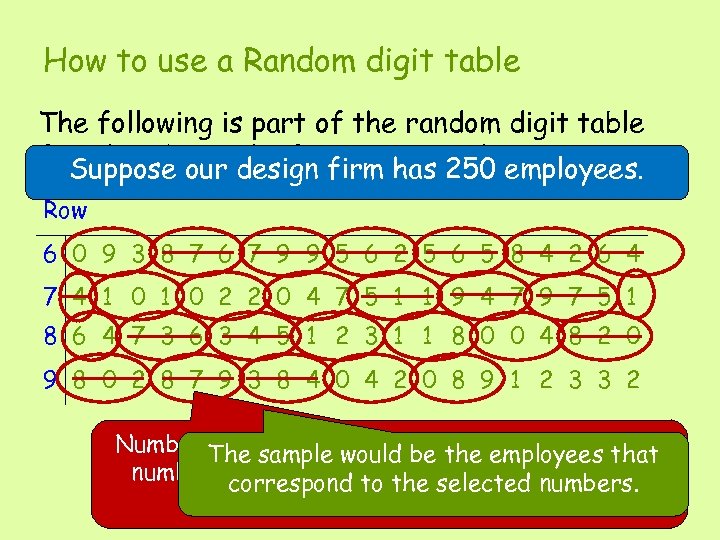
How to use a Random digit table The following is part of the random digit table found in the back of your textbook: employees. Suppose our design firm has 250 Row 6 0 9 3 8 7 6 7 9 9 5 6 2 5 6 5 8 4 2 6 4 7 4 1 0 2 2 0 4 7 5 1 1 9 4 7 9 7 5 1 8 6 4 7 3 6 3 4 5 1 2 3 1 1 8 0 0 4 8 2 0 9 8 0 2 8 7 9 3 8 4 0 4 2 0 8 9 1 2 3 3 2 Number The samplefrom 1 be 250. employees that employees would to the Select 3 -digit numbers correspond to the selected numbers. from the table. If the number is not within 1 -250, ignore it.
Sampling with replacement Sampling in which an individual or object, once selected, is put back into the population before the next selection. This allows an object or individual to be selected more than once for a sample. In practice, sampling with replacement is rarely used.

Sampling without replacement Sampling in which an individual or object, once selected, is NOT put back into the population before In practice, sampling without the next selection. replacement is more common. That is once an individual or object is selected, they are not replaced and cannot be selected again. Although sampling with and without replacement are different, they can be treated as the same when the sample size n is relatively small compared to the population size (no more than 10% of the population).
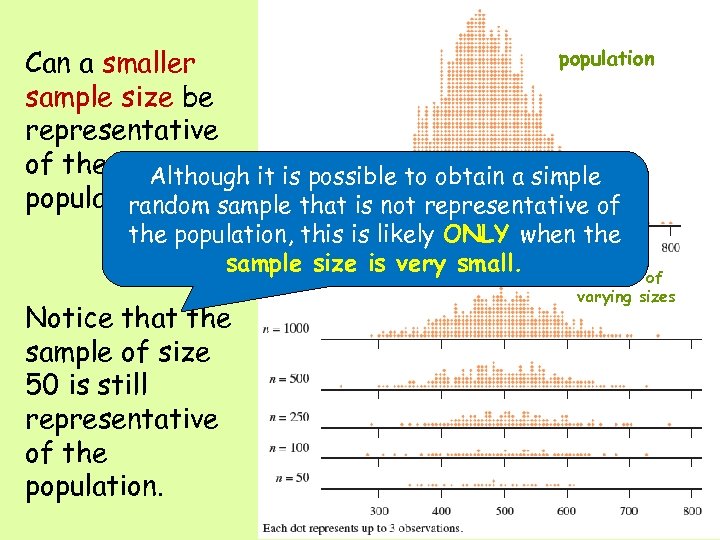
population Can a smaller sample size be representative of the Although it is possible to obtain a simple population? random sample that is not representative of the population, this is likely ONLY when the sample size is very small. Notice that the sample of size 50 is still representative of the population. Samples of varying sizes

Now let's Random at other Stratified take a look. Sample sampling methods. The population is first divided into nonoverlapping subgroups (called strata). Then separate simple random samples are selected from each subgroup (stratum). Suppose we wanted to estimate the average cost of The real Strata are subgroupssampling isa malpractice insurance for doctorsare that it advantage of stratified that in particular city. Wemake more accurate inferencesof the population often allows you to could view based upon similar (homogeneous) all doctors in this than does simple into one of four about a population city as falling random sampling. some random sampling is often easier of the group Stratified characteristicinternists and family subgroups: (1) surgeons, (2) members. Into implement obstetricians, and relatively general, it is and is more cost effective practitioners, (3)much easier to produce(4) all other accurate estimates of characteristics doctors. than simple random sampling. of a homogeneous group than of a heterogeneous group.

Cluster Sampling Sometimes it is easier to select groups of Cluster sampling divides the population of is to individuals from a population than it interest into nonoverlapping subgroups, called select individuals themselves. clusters. Which would be easier to do? Clusters are then selected at random, and ALL individualsrandomly selected individuals are included in A) Find 75 in the selected clusters the. Find 3 randomly selected homerooms B) sample. Suppose that a large urban high school hasis when each The ideal situation for Randomly selecting 3 senior cluster sampling 600 senior students, mirrors the are enrolled in aofthenperiod all cluster all of whom characteristics first population. homerooms and the include homeroom. There are 24 the students in the each with senior homerooms, selected approximately 25 students. The school administrators homerooms in the sample. want to select a sample of roughly 75 seniors to participate in a survey.
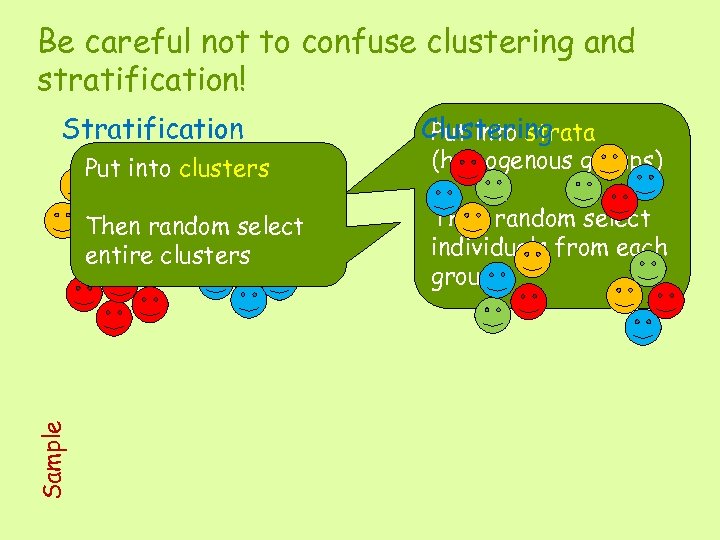
Be careful not to confuse clustering and stratification! Stratification Clustering Put into strata (homogenous groups) Then random select entire clusters Sample Put into clusters Then random select individuals from each group

1 in k Systematic Sampling Selects an ordered arrangement from a population by • first choosing a starting point at random from the first k individuals • then every k th individual after that k is often selected so that sample of faculty Suppose you wish to select aa certain sample members from size faculty phone directory. You the is produced. Let first randomly select a faculty would N = population size and n = sample size. from the first works = 20) faculty listedlong as This method 20 (k reasonably well as = select in the directory. krepeating patterns in the 20 th there are no Then. N ÷ n every faculty after that on the list. population list.

Convenience Sampling Selecting individuals or objects that are easy or convenient to sample. Suppose your statistics professor asked you to gather a sample of 20 students from your college. You survey 20 students in your next class which is music theory. Will this sample be representative of the population of all sampling is rarely college? Why Convenience students at your representative or why not? of the population, so DON’T USE IT!

Voluntary response is a type of convenience sampling which relies solely on individuals volunteering to be part of the study. People who are motivated to volunteer responses often hold strong opinions. It is extremely unlikely that they are representative of the population!

Identify the sampling method 1)The Educational Testing Service (ETS) needed a sample of colleges. ETS first divided all colleges into 6 subgroups of similar types (small public, small private, medium public, medium private, large public, and large private). Then they randomly selected 3 colleges from each group. Stratified random sample

Identify the sampling design 2) A county commissioner wants to survey people in her district to determine their opinions on a particular law up for adoption. She decides to randomly select blocks in her district and then survey all who live on those blocks. Cluster sample

Identify the sampling design 3) A local restaurant manager wants to survey customers about the service they receive. Each night the manager randomly chooses a number between 1 & 10. He then gives a survey to that customer, and to every 10 th customer after them, to fill it out before they leave. Systematic sampling

Consider the following example: In 1936, Franklin Delano Roosevelt had been President for one term. The magazine, The Literary Digest, predicted that Alf Landon would beat FDR in that year's election by 57 to 43 percent. The Digest mailed over 10 million questionnaires to names drawn from lists of automobile and telephone owners, and over 2. 3 million people responded - a huge sample. Bias same time, a young for samples to differ At the is the tendencyman named George Gallup sampledthe corresponding population in some from only 50, 000 people and predicted that Roosevelt would win. Gallup's prediction was ridiculed systematic way. as naive. After all, the Digest had predicted the winner in every election since classic example of its predictions on This is a 1916, and had based how bias affects the largest response to any poll in history. the results of a sample! But Roosevelt won with 62% of the vote. The size of the Digest's error is staggering.
Sources of bias Selection bias • Occurs when the way the sample is selected systematically excludes some part of the Suppose you take population of interesta sample by randomly selecting names from • May also occur if only volunteers or selfthe phone book – some selected individuals are used in a study groups will not have the opportunity of being selected!

Sources of bias Measurement wanted to survey high school Suppose we or Response bias A Gallup survey sponsored by thewe used a students asked if they and American Paper People are on drug abuse can trust men in Institute (Wall 17, 1994) • Occurs when –Street Journal, Mayinterviewincluded the method of observation tends uniformed the interviewer is a man with officer to mustaches police “It is estimated that disposable the following question: to produce values that sample – would differ each student inmustache. 2% of the we in our systematically trash afor less than diapers accounts from thelandfills. honest some beverage containers, true valuecontrast, way get In in answers? today’s – Improperly calibrated scale is used to weigh items third-class mail and yard waste are estimated to – Tendency of people of to be completely Given account for about 21%not trash in landfills. honestthis, when asked would it be behavior or unpopular in your opinion, about illegal fair to tax or ban disposable beliefs diapers? ” – Appearance or behavior of the person asking the questions – Questions on a survey are worded in a way that tends to influence the response

Sources of bias Nonresponse • occurs when responses are not obtained from all individuals selected for inclusion in the sample The How might this follow-up be done? the phone rings – you answer. “Hello, ” person says, “do you have time for a • To minimize nonresonse bias, it is critical that survey about radio stations? ” a serious effort be made to follow up with You hang up! individuals who did not respond to the initial request for information

Sources of bias Will increasing the sample size reduce the effects of bias in the study? No, it does nothing to reduce bias if • The method of selection is flawed • If non-response is high

Identify one potential source of bias. Suppose that you want to estimate the total amount of money spent by students on textbooks each semester at a local college. You collect register receipts for students as they leave the bookstore during lunch one day. Convenience sampling – easy way to collect data or Selection bias – students who buy books from on-line bookstores are excluded.

Identify one potential source of bias. To find the average value of a home in Plano, one averages the price of homes that are listed for sale with a realtor. Selection bias – leaves out homes that are not for sale or homes that are listed with different realtors. (other answers are possible)

The article “What People Buy from Fast-Food Restaurants: Caloric Content and Menu Item Selection” (Obesity [2009]: 1369 -1374) reported that the average number of calories consumed at lunch in New Your City fast-food restaurants was 827. The researchers selected 267 fast-food locations at random. The paper states that at each of these locations “adult” customers were approached as they entered the restaurant and asked to provide their food receipt when exiting and to complete a brief survey. Will this study result in data that is representative of the population?

Question Response What is the population The people who eat at fast-food restaurants in NYC of interest? Was the sample selected in a reasonable way? Yes – because the researchers randomly selected the fast-food restaurants, this is a reasonable way to select the sample Is the sample likely to be representative of the population of interest? Yes – because the researchers randomly selected the fast-food restaurants, it is reasonable to regard the people eating at these locations as representative Are there any obvious sources of bias? Two potential sources of bias • Response bias since customers were approached before they ordered • Nonresponse – some people refused to participate

Experimental Design

Experiments Suppose we are interested in determining the effect of room temperature on the performance on a first-semester calculus exam. So we decide to perform an experiment. explanatory variable. This is called the What variable will variables – those variables that have Explanatory we “measure”? values that are controlled by the experimenter the performance on a calculus exam (also called factors) This is called the response variable. What variable will “explain” the Response variable –calculus exam? not results on the a variable that is controlled by the experimenter and that is the room temperature measured as part of the experiment

Room temperature experiment continued. . . We decide to use two temperature settings, 65° and 75°. How many treatments would our experiment have? the 2 treatments are the 2 temperature settings Experimental condition – any particular combination of the explanatory variables (also called treatments)

Room temperature experiment continued. . . Suppose. This have example of a confounding variable. we is an 10 sections of first-semester calculus that have agree to participate in our study. Confounding variable – two variables are On whoconfounded when their effects on the response or what will we impose the treatments? can NOT be distinguished. the 10 sections of calculus Should the instructors of these sections be allowed to select to which room temperature that their sections are assigned? No, since the instructor would probably select the These are our subjects or experimental units. same temperature for all their sections, then it would be difficult to tell if the scores are due to the temperature the instructor’s which a Experimental units – or tosmallest unit to teaching style treatment is applied.

Designing Strategies for Single Comparative Experiments The goal of a single comparative experiment is to determine the effects of the treatment on the response variable. To do this: You must consider other potential sources of variability in the response • Eliminate them OR • Ensure they produce chance-like variability
Room temperature experiment continued. . . Remember – the explanatory variable is the room In an experiment, these otherand 75°. need temperature setting, 65° variables The to be “controlled”. response variable is the grade on the calculus What about Can the experimenter the variables that the exam. Direct control is holding the other these other experimenter control variables can’t directly control? constant so that their effects areto avoid What can be done If so, how? variables? not confounded with those of the experimental confounding results? Are there other variables that could affect the conditions (treatments). response? Instr uctor ? tb day? ex e of T Tim Ability level of student s? ? ok o

Room temperature experiment continued. . . Remember – the explanatory variable is the room temperature setting, 65° and 75°. The response variable is the grade on the calculus exam. The experimenter cannot control who the instructors are. Therefore, the instructors may be potentially confounding. Another way to control a variable is to block by that variable. Instr uctor k? ? We use each instructor as his/her ownoblock. o ay? tb of d Then sections of each instructor will be ex me T Ti Ab lity randomly iassigned to the two treatments. level of student s?

Room temperature experiment continued. . . What about other variables that we cannot control directly or that we don’t even think about? Random assignment should evenly spread all other variables, that are not controlled directly, into all treatment groups. We expect these variables to affect all the experimental groups in the same way; therefore, their effects are not confounding.

Room temperature experiment continued. . . To randomly assign the 10 sections of first- of Place the numbers 1 -10 on identical slips semester calculusput the 2 treatment groups, we paper and to them in a hat. Mix well. would first number the classes 1 -10. There are 10 sections. Sections assigned 5 8 7 3 9 This is Treatment 1 (65°) 9 Replication ensures called replication. 3 7 5 8 that there is an adequate number of Treatment 2 (75°) 1 2 4 6 10 observations for each experimental condition. Randomly select 5 numbers from the hat. The remaining sections will have the room Those will be the sections at 75°. temperature set that have the room temperature set at 65°.

Key Concepts of Experimental Design Direct control holds potential confounding variables constant so their effects are not confounded with the treatments. Blocking uses potentially confounding variables to create groups (blocks) that are similar. All experimental conditions (treatments) are then tried in each block. Random assignment removes the potential for confounding variables by creating equivalent experimental groups Random assignment is a an adequate Replication ensures that there is critical component of a good experiment. number of observations for each treatment.

What to do with Potentially Confounding Variables Potentially confounding variables that are known and incorporated into the experimental design: Use: • Direct control – hold potentially confounding variables fixed • Blocking – allow for valid comparisons because each treatment is tried in each block Potentially confounding variables that are NOT known or NOT incorporated into the experimental design: Use: • Random assignment
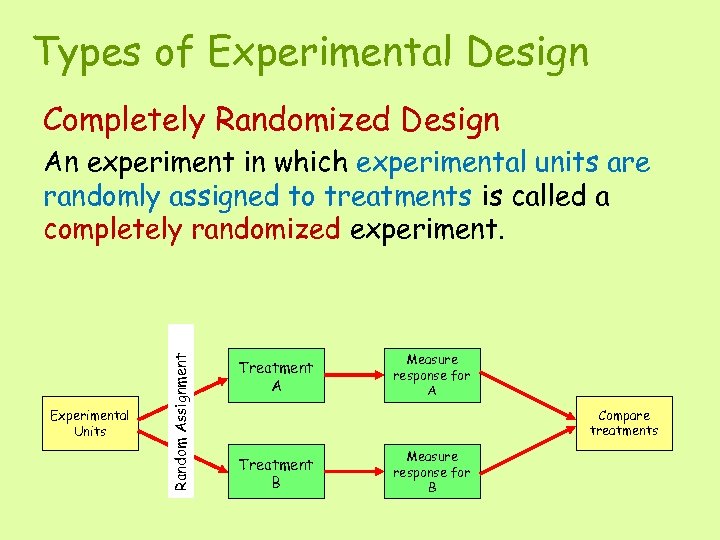
Types of Experimental Design Completely Randomized Design Experimental Units Random Assignment An experiment in which experimental units are randomly assigned to treatments is called a completely randomized experiment. Treatment A Measure response for A Compare treatments Treatment B Measure response for B
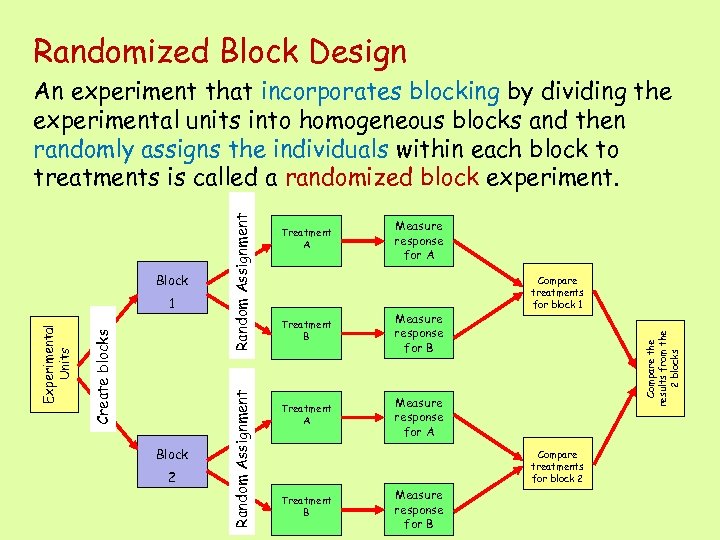
Randomized Block Design Block 2 Treatment A Measure response for A Treatment B Measure response for B Treatment A Compare treatments for block 1 Measure response for A Compare the results from the 2 blocks Create blocks Experimental Units 1 Random Assignment Block Random Assignment An experiment that incorporates blocking by dividing the experimental units into homogeneous blocks and then randomly assigns the individuals within each block to treatments is called a randomized block experiment. Compare treatments for block 2 Treatment B Measure response for B

Can moving their hands help children learn math? An experiment was conducted to compare two different methods for teaching children how to solve math problems of the form 3 + 2 + 8 = ___ + 8. One method involved having students point to the 3 + 2 on the left side of the equal sign with one hand then point to the blank on the right side of the equal sign before filling in the blank to complete the equation. The other method did not involve using these had gestures. To compare the two methods, 128 children, ages 9 and 10, were randomly assigned to the two experimental conditions. This is an example of what type of experimental design? Completely Randomized Design
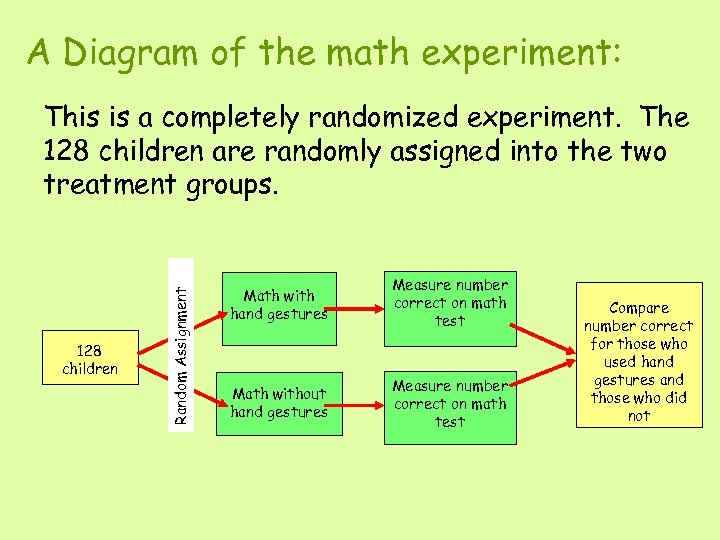
A Diagram of the math experiment: 128 children Random Assignment This is a completely randomized experiment. The 128 children are randomly assigned into the two treatment groups. Math with hand gestures Measure number correct on math test Math without hand gestures Measure number correct on math test Compare number correct for those who used hand gestures and those who did not

Can moving their hands help children learn math? Suppose that you were worried that gender might also be related to performance on the math test. One possibility would be to use direct control of gender – use only boys or only girls. But, any conclusions can ONLY be generalized to the group that was used. Another strategy is to incorporate blocking into the design. The researchers could create two blocks, one consisting of girls and one consisting of boys. Then, once the blocks are formed, randomly assign the girls to the two treatments and randomly assign the boys to the two treatments. This is an example of a Randomized Block Design.
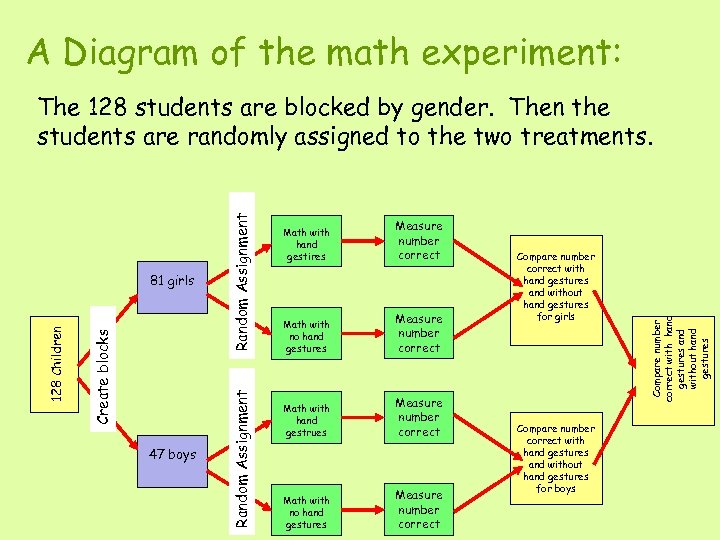
A Diagram of the math experiment: 47 boys Math with hand gestires Measure number correct Math with no hand gestures Measure number correct Math with hand gestrues Measure number correct Math with no hand gestures Measure number correct Compare number correct with hand gestures and without hand gestures for girls Compare number correct with hand gestures and without hand gestures for boys Compare number correct with hand gestures and without hand gestures Random Assignment Create blocks 128 Children 81 girls Random Assignment The 128 students are blocked by gender. Then the students are randomly assigned to the two treatments.

Revisit the room temperature experiment. . . In the room temperature experiment, we have only 2 treatment groups, 65° and 75°. We do NOT have a control group. Control group A control group - is an experimental group that does NOT receive assess how the • allows the experimenter toany treatment. response variable behaves when the treatment is notexperiments that use human subjects, the In used. • provides a baseline against which the use of a placebo may be necessary. treatment groups can be compared to determine that is the treatment A placebo is somethingwhether. IDENTICAL to had an effect. the treatment received, except it contains NO active ingredients.

Consider Anna, a waitress. She decides to perform an experiment to determine if writing “Thank you” on the receipt increases her tip percentage. She plans on having two groups. On one group she will write “Thank you” on the receipt and on the other group she will not write “Thank you” on the receipt. Which of these is the control group?

Room temperature experiment continued. . . Would the students in each section of calculus know to which treatment group, 65° or 75°, they were assigned? If the students knew about the experiment, they would probably know which treatment group they were in. A double-blind experiment is one in which An So this experiment the individualsdo experiment in which the subjects neither the subjects nor is probably NOT not blinded. know which response they which who measure thetreatmentknowswere in is called a single-blind experiment. treatment is received.

Using Volunteers as Subjects in an Experiment Remember – Using volunteers in observational studies is never a good idea! However – It is common practice to use volunteers as subjects in an experiment. • Random assignment of the volunteers to treatments allows for cause-and-effect conclusions • But, limits the ability to generalize to population

The ONLY way to show a cause-effect relationship is with a well-designed, well-controlled experiment!!!

Chilling newborns? Researchers for the National Institute of Child Health and Human Development studied 208 infants whose brains were temporarily deprived of oxygen as a result of complications at birth (The New England Journal of Medicine, October 13, 2005). These babies were subjects in an experiment to determine if reducing body temperature for three days after birth improved their chances of surviving without brain damage. The experiment was summarized in a paper that stated “infants were randomly assigned to usual care (control group) or whole-body cooling. ” The researchers recorded whether the infant survived (yes/no) and if the infant had brain damage (yes/no). Let’s examine this experiment.
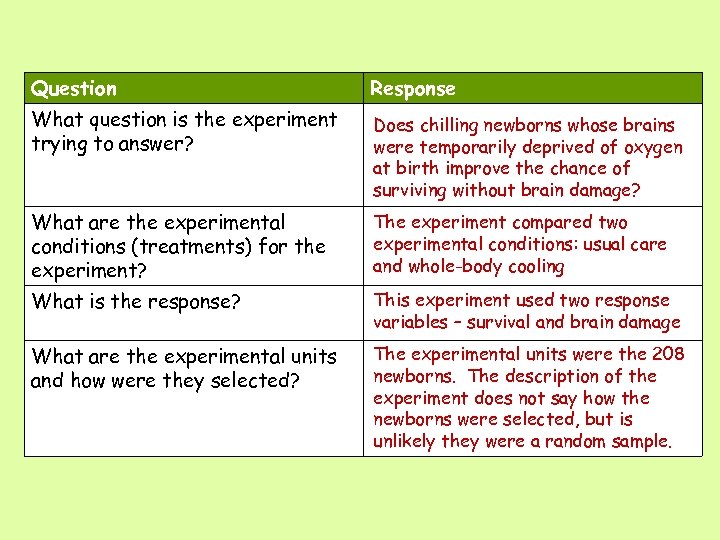
Question Response What question is the experiment trying to answer? Does chilling newborns whose brains were temporarily deprived of oxygen at birth improve the chance of surviving without brain damage? What are the experimental conditions (treatments) for the experiment? The experiment compared two experimental conditions: usual care and whole-body cooling What is the response? This experiment used two response variables – survival and brain damage What are the experimental units and how were they selected? The experimental units were the 208 newborns. The description of the experiment does not say how the newborns were selected, but is unlikely they were a random sample.

Table Continued. . . Question Response Does the design incorporate random Yes, the babies were randomly assignment of experimental units to assigned to one of the two the different experimental conditions? If not, are there potentially confounding variables that would limit the use of these Because this is a well-designed data? Does the experiment, researchers were able to experiment incorporate a In this experiment, the usual care control group and/or a placebo group serves as a control group. use the resulting data to conclude that group? If not, would the cooling did by including experiment be improvedreduce the risk of death and them? disability of infants deprived of oxygen Does the experiment involve This experiment did not involve at birth. blinding? If not, would the blinding. It might have been possible experiment be improved by making to blind the person who makes the it single- or double-blind? assessment of whether or not there was brain damage, but this probably isn’t necessary in this experiment.

s) eles Time ng IQ (Los A ’s rs a Child we panking Lo S Spanking can lower IQ (NBC 4 i, Colum bus, Ohio ) ) ientist. com sc s’ IQ (new id king hits k Smac In this study, the investigators followed 806 kids ages 2 to 4 and 704 kids ages 5 to 9 for 4 years. IQ was measured at the beginning of the study and again 4 years These headlines all imply that spanking later. The researchers found that at the end of the was the of the younger kids who were not study, the average IQ cause of the observed spanked was 5 pointsdifference that of kids who were higher than in IQ. spanked. For. Is this conclusion reasonable? kids who the older group, the average IQ of were not spanked was 2. 8 points higher.

Drawing Conclusions from Statistical Studies Type of Conclusion Reasonable When Generalize from sample to population Random selection is used to obtain the sample Change in response is caused by experimental conditions (causeand-effect conclusion) There is random assignment of experimental units to experimental conditions This table implies the following: • For observational studies, it is not possible to reach cause-and-effect conclusions, but it is possible to generalize from the sample to the population of interest if the study design incorporated random selection. • For experiments, it is possible to reach cause-and-effect conclusions if the study design incorporated random assignment to experimental conditions. • If an experiment incorporates both random assignment to experimental conditions and random selection of experimental units from some population, it is possible to reach cause-and-effect conclusions and to generalize to the population from which the experimental units were selected.

s) eles Time ng IQ (Los A ’s rs a Child we panking Lo S Spanking can lower IQ (NBC 4 i, Colum bus, Ohio ) ) ientist. com sc s’ IQ (new id king hits k Smac Revisit. . . In this study, the investigators followed 806 kids ages 2 to 4 and 704 kids ages 5 to 9 for 4 years. IQ was measured at the beginning of the study and again 4 years These conclusions are not reasonable later. The researchers found that at the end of the since this study has no random study, the average IQ of the younger kids who were not assignment of experimental units to spanked was 5 points higher than that of kids who were experimental conditions. spanked. For the older group, the average IQ of kids who were not spanked was 2. 8 points higher.

Avoid These Common Mistakes

Avoid These Common Mistakes 1. Drawing a cause-and-effect conclusion from an observational study. Don’t this! do Don’t b elieve i t when o thers d o!

Avoid These Common Mistakes 2. Generalizing results of an experiment that uses volunteers as subjects. Only do this if it can be convincingly argued that the group of volunteers is representative of the population of interest.

Avoid These Common Mistakes 3. Generalizing conclusions based on data from a poorly designed observational study. Generalizing from a sample to a population is justified only when the sample is representative of the population. This would be the case if the sample was a random sample from the population, and there were no major potential sources of bias.

Avoid These Common Mistakes 4. Generalizing conclusions based on an observational study that used voluntary response or convenience sampling to a larger population. This is almost never reasonable!
4f97bc90be1fa6f904308fa5f6a52240.ppt