Chapter 1 Appendix Time Value of Money The

Chapter 1 Appendix Time Value of Money: The Basics Mc. Graw-Hill/Irwin Copyright © 2010 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Time Value of Money • Answers the questions: – “If I deposit $10, 000 today, how much will I have for a down payment on a house in 5 years? ” – “Will $2, 000 saved each year give me enough money when I retire? ” – “How much must I save today to have enough for my children’s education? ” App 1 -2

Time Value of Money Basic Principles – A dollar received today is worth more than a dollar received a year from today – A dollar that will be received in the future is worth less than a dollar today – Why? • A dollar today could be saved or invested • A dollar in the future is uncertain App 1 -3

Time Value of Money • Definitions • Solving TVM Problems – Types of Problems • • Interest rate basics - Simple interest Future value - Single amount & Annuity Present value - Single amount & Annuity Calculating Loan payments – Solutions Methods • Formulas • TVM Tables • Financial Calculator App 1 -4

Basic TVM Definitions • Future Value (FV) – The increased value of money from interest earned – The amount to which a current sum will grow given a certain interest rate and time period – “Compounding” • Present Value (PV) – The current value of a future amount given a certain interest rate and time period – “Discounting” App 1 -5

Basic TVM Definitions • Payment (PMT or annuity) – Amount of annuity deposit or withdrawal • Sign Convention: – Applies to PV, PMT and FV – Positive = inflow to YOU • Money received as a loan is an inflow – Negative = outflow from YOU • Deposit to an account is an outflow App 1 -6

Basic TVM Definitions • Interest rate (i or I/Y) – Stated as a percent per year – Also called “discount rate” – 12% = • “ 0. 12” in formulas • “ 12” in financial calculators App 1 -7

Basic TVM Definitions • Time Periods (n or t) – Expressed in years • 3 months = “ 0. 25” years • 2 ½ years = “ 2. 5” years – Interest rate and time period must match • Annual periods annual rate • Monthly periods monthly rate App 1 -8

Single Amount & Annuities • Single Amount: – A single payment made or received at one time – Calculator: PMT=0 • Annuity: – Finite series of equal payments that occur at regular intervals – PMT key used – Sign convention is important App 1 -9

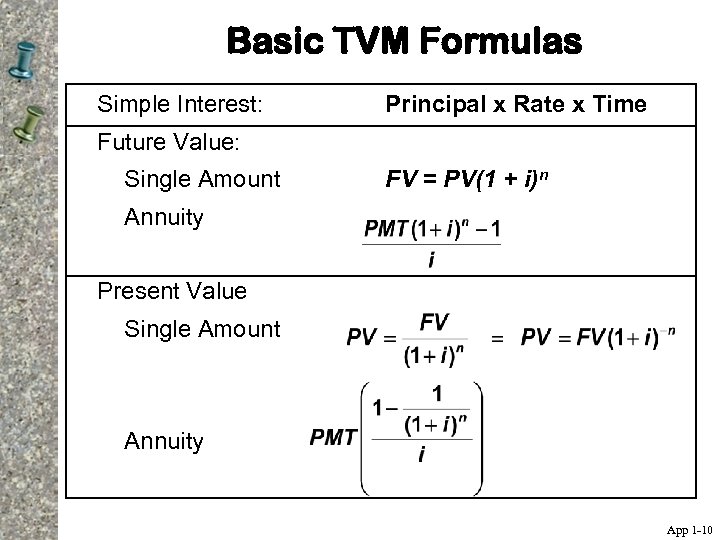Basic TVM Formulas Simple Interest: Principal x Rate x Time Future Value: Single Amount FV = PV(1 + i)n Annuity Present Value Single Amount Annuity App 1 -10

TVM Calculator Solutions Texas Instruments BA-II Plus • • • FV = future value One of these MUST be negative PV = present value PMT = periodic payment I/Y = interest rate N = number of periods N I/Y PV PMT FV App 1 -11

Texas Instruments BA-II Plus • I/Y = period interest rate (i) – P/Y must = 1 – Interest is entered as a percent, not a decimal • 5% interest = “ 5”, not “ 0. 05” • Clear the registers before each problem – [2 nd] [CLR TVM] – Or reenter each field App 1 -12

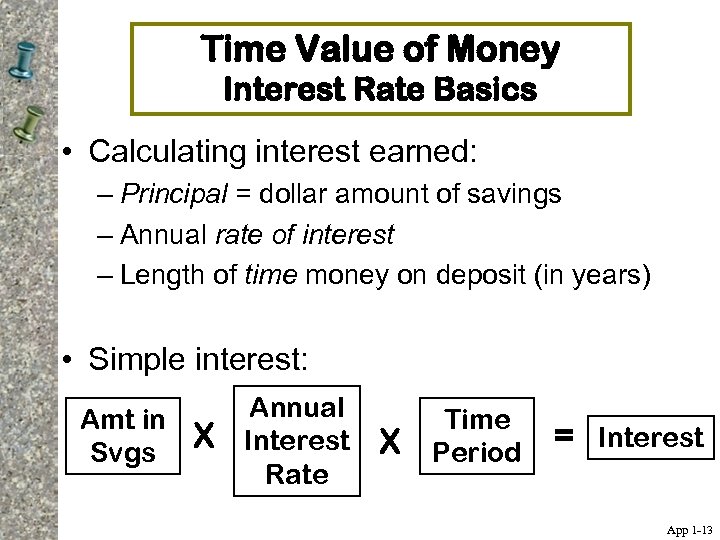Time Value of Money Interest Rate Basics • Calculating interest earned: – Principal = dollar amount of savings – Annual rate of interest – Length of time money on deposit (in years) • Simple interest: Amt in Svgs X Annual Interest Rate X Time Period = Interest App 1 -13

Interest Rate Basics Example A You borrow $1, 000 at 5% annual interest for 1 year: Principal = $1, 000 Interest rate = 5% =. 05 Time period = 1 $1, 000 X . 05 X 1 = $50 App 1 -14

Interest Rate Basics Example B You deposit $750 at 8% per year for 9 months: Principal = $750 Interest rate = 8% Time period = 9/12 =. 75 $750 X . 08 X 0. 75 = $45 App 1 -15

Interest Rate Basics Example B – Calculator* Principal = $750 Interest rate = 8% Time period = 9/12 =. 75 Calculator Solution Keystrokes n n n . 75 8 -750 0 CPT N I/Y PV PMT FV = 794. 56 – 750 = 44. 56 ≈ 45 *Calculator solutions match the TI Business Analyst II+. Keystroke adjustments may need to be made for other financial calculators App 1 -16

Interest Rate Basics Example B – Calculator Solution n n ** . 75 8 -750 0 CPT N I/Y PV ** PMT FV = 794. 56 – 750 = 44. 56 ≈ 45 Remember: when using a financial calculator, either PV or FV must be negative. • Outflows (from you) are negative • Inflows (to you) are positive • Depositing money in an account is an outflow App 1 -17

Future Value of a Single Amount • Amount to which current savings will increase • = Original amount + compounded interest • = Compounding • Formula Solution: • Table Solution: • Calculator Solution: N I/Y PV PMT CPT FV App 1 -18

Future Value of a Single Amount Formula & TVM Table Solutions Example C • Suppose you invest $1 for 3 years at 10% • How much would you have? Formula Solution: FV TVM Tables Solution: =PV(1+i)n Exhibit 1 -A =1(1. 10)3 Periods = 3 =1(1. 331) Rate = 10% =1. 331 Factor = 1. 331 FV = PV(Factor) FV = 1(1. 331) FV = 1. 331 App 1 -19

Future Value of a Single Amount Calculator Solution Example C • Suppose you invest $1 for 3 years at 10%. How much would you have? Calculator Solution n 3 N n 10 I/Y n -1 PV n 0 PMT n CPT FV = 1. 331 App 1 -20

Future Value of a Single Amount Formula & TVM Tables Example D • Your savings of $400 earns 12% compounded monthly (=1% per month) • How much would you have after 18 months? • Table Hint: Use 1% and 18 periods Formula Solution: FV =PV(1+i)n =400(1. 01)18 TVM Tables Solution: Exhibit 1 -A Periods = 18 Rate = 1% =400(1. 196) Factor = 1. 196 =478. 46 FV = 400(1. 196) FV = 478. 40 App 1 -21

Future Value of a Single Amount Calculator Solution Example D • Suppose you invest $400 for 18 months at 12% compounded monthly. How much would you have? Calculator Solution n 18 N n 1 I/Y n -400 PV n 0 PMT n CPT FV = 478. 46 App 1 -22

Future Value of a Series of Equal Amounts • “Annuity” = series of equal deposits at equal intervals earning a constant rate – Equal annuity deposit amounts = PMT • Formula Solution: • Table Solution: • Calculator Solution: N I/Y PV PMT CPT FV App 1 -23

Future Value of a Series of Equal Amounts Formula & TVM Tables Example E • What is the future value of three $1 deposits made at the end of the next three years, earning 10% interest? Formula Solution: TVM Tables Solution: Exhibit 1 -B Periods = 3 Rate = 10% Factor = 3. 31 FV = 1(3. 31) FV = 3. 31 App 1 -24

Future Value of a Series of Equal Amounts Calculator Solution Example E Calculator Solution n 3 N n 10 I/Y n 0 PV n -1 PMT* n CPT FV = 3. 31 * Note that the PMT value is negative since it is an outflow/deposit. App 1 -25

Future Value of a Series of Equal Amounts Formula & TVM Tables Example F • What is the future value of ten $40 deposits earning 8% compounded annually? Formula Solution: TVM Tables Solution: Exhibit 1 -B Periods = 10 Rate = 8% Factor = 14. 487 FV = 40(14. 487) FV = 579. 48 App 1 -26

Future Value of a Series of Equal Amounts Calculator Solution Example F Calculator Solution n 10 N n 8 I/Y n 0 PV n -40 PMT n CPT FV = 579. 46 App 1 -27

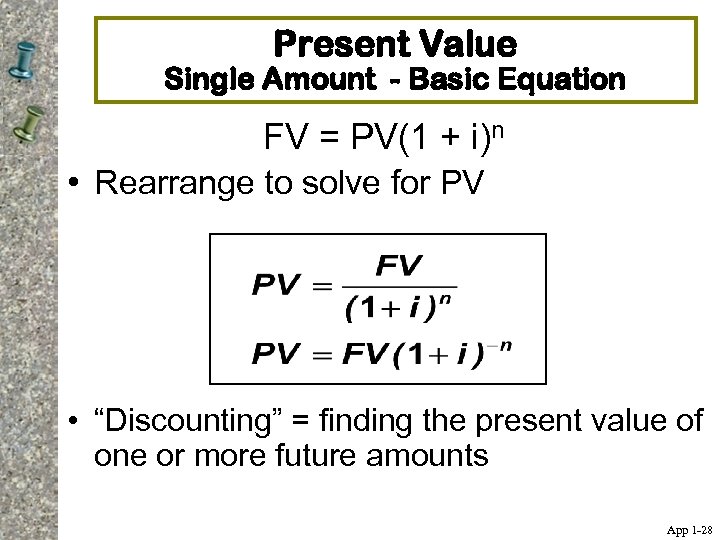Present Value Single Amount - Basic Equation FV = PV(1 + i)n • Rearrange to solve for PV • “Discounting” = finding the present value of one or more future amounts App 1 -28

Present Value of a Single Amount • Formula Solution: • Table Solution: • Calculator Solution: N I/Y PMT FV CPT PV App 1 -29

Present Value of a Single Amount Formula & TVM Tables Example G • What is the present value of $1 to be received in 3 years at a 10% interest rate? TVM Tables Solution: Formula Solution: PV Exhibit 1 -C =FV/(1+i)n Periods = 3 =1/(1. 10)3 Rate = 10% =1*(. 7513) Factor =. 751 =0. 7513 PV = FV*(Factor) PV = 1*(0. 751) PV = 0. 751 App 1 -30

Present Value of a Single Amount Example G Formula Solution: PV =FV/(1+i)n =1/(1. 10)3 =1*(0. 7513) =0. 7513 TVM Tables Solution: Exhibit 1 -C Periods = 3 (down left column) Rate = 10% (across top) Factor =. 751 Calculator Solution n n 3 10 CPT 0 1 N I/Y PV = -. 7513 PMT FV PV = FV(Factor) PV = 1(0. 751) PV = 0. 751 App 1 -31

Present Value of a Single Amount Example H You want to have $300 seven years from now. Your savings earns 10% compounded semiannually. How much must you deposit today? Formula Solution: PV =FV/(1+i)n =300/(1. 05)14 =300/(1. 9799) =151. 52 TVM Tables Solution: Exhibit 1 -C Periods = 14 (down left column) Rate = 5% (across top) Calculator Solution n 14 N n 5 I/Y n CPT PV = 151. 52 n 0 PMT n 300 FV Factor =. 505 PV = FV(Factor) PV = 300 x (0. 505) PV = $151. 50 App 1 -32

Present Value of a Series of Equal Amounts • Annuity • Table Factors = Exhibit 1 -D • Formula Solution: • Table Solution: • Calculator Solution: N I/Y PMT FV CPT PV App 1 -33

Present Value of an Annuity Example I • You wish to withdraw $1 at the end of each of the next 3 years. (= an Inflow) • The account earns 10% compounded annually. • How much do you need to deposit today to be able to make these withdrawals? 3 N; 10 I/Y; 1 PMT; CPT PV = -2. 48685 FV 0 Exhibit 1 -D: Row 3, column 10% Factor = 2. 487 PV = PMT*(Factor) = 1*(2. 487) PV = $2. 49 App 1 -34

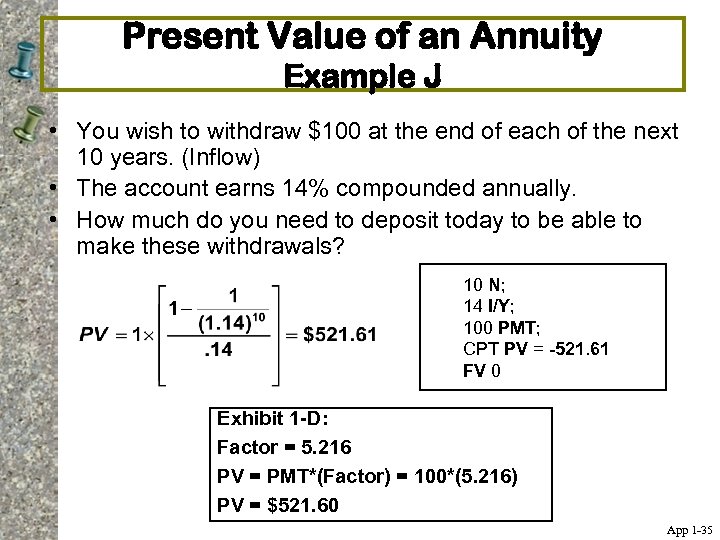Present Value of an Annuity Example J • You wish to withdraw $100 at the end of each of the next 10 years. (Inflow) • The account earns 14% compounded annually. • How much do you need to deposit today to be able to make these withdrawals? 10 N; 14 I/Y; 100 PMT; CPT PV = -521. 61 FV 0 Exhibit 1 -D: Factor = 5. 216 PV = PMT*(Factor) = 100*(5. 216) PV = $521. 60 App 1 -35

Using Present Value to Determine Loan Payments Example K If you borrow $1, 000 with a 6% interest rate to be repaid in three equal payments at the end of the next three years, what will the annual payment be? • Table Solution: • Calculator Solution 3 N; 6 I/Y; CPT PMT = 374. 10981 PV = 1000 FV 0 App 1 -36