Chalmers University of Technology Lecture 7 Axial

Chalmers University of Technology Lecture 7 – Axial flow turbines • Discussion on design task 1 • Elementary axial turbine theory – Velocity triangles – Degree of reaction – Blade loading coefficient, flow coefficient • Problem 7. 1 • Some turbine design aspects – Choice of blade profile, pitch and chord

Chalmers University of Technology Axial flow turbines • Working fluid is accelerated by the stator and decelerated by the rotor • Boundary layer growth and separation does not limit stage loading as in axial compressor • Expansion occurs in stator and in relative frame of rotor

Chalmers University of Technology Elementary theory • Energy equation for control volumes (again): • Adiabatic expansion process (work extracted from system sign convention for added work = +w) – Rotor => -w = cp(T 03 -T 02) <=> w = cp(T 02 -T 03) – Stator => 0 = cp(T 02 -T 01) => T 02= T 01

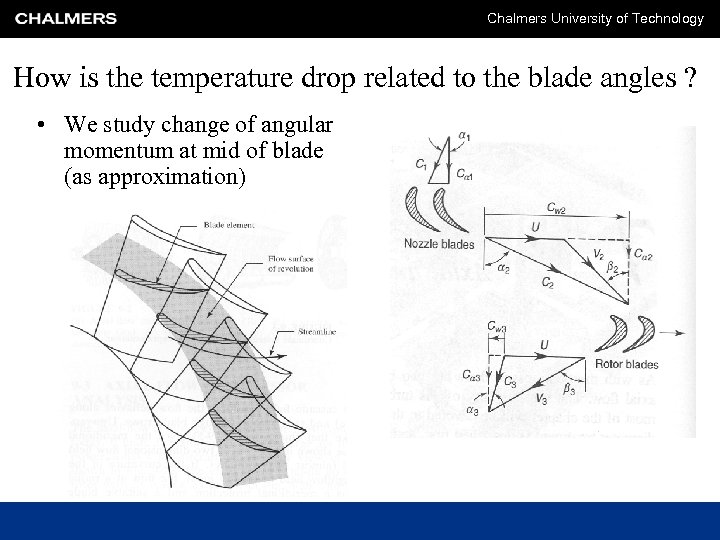Chalmers University of Technology How is the temperature drop related to the blade angles ? • We study change of angular momentum at mid of blade (as approximation)

Chalmers University of Technology Governing equations and assumptions • Relative and absolute refererence frames are related by: • We only study designs where: – Ca 2=Ca 3 – C 1=C 3 • You should know how to extend the equations!!! • We repeat the derivation of theoretical work used for radial and axial compressors:

Chalmers University of Technology Principle of angular momentum Stage work output w: Ca constant:

Chalmers University of Technology

Chalmers University of Technology Energy equation Combine derived equations => Energy equation: We have a relation between temperature drop and blade angles!!! : Exercise: derive the correct expression when 3 is small enough to allow 3 to be pointing in the direction of rotation.

Chalmers University of Technology Dimensionless parameters Blade loading coefficient, temperature drop coefficient: Degree of reaction: Exercise: show that this expression is equal to => when C 3= C 1

Chalmers University of Technology can be related to the blade angles! C 3 = C 1 => Relative to the rotor the flow does no work (in the relative frame the blade is fixed). Thus T 0, relative is constant => Exercise: Verify this by using the definition of the relative total temperature:

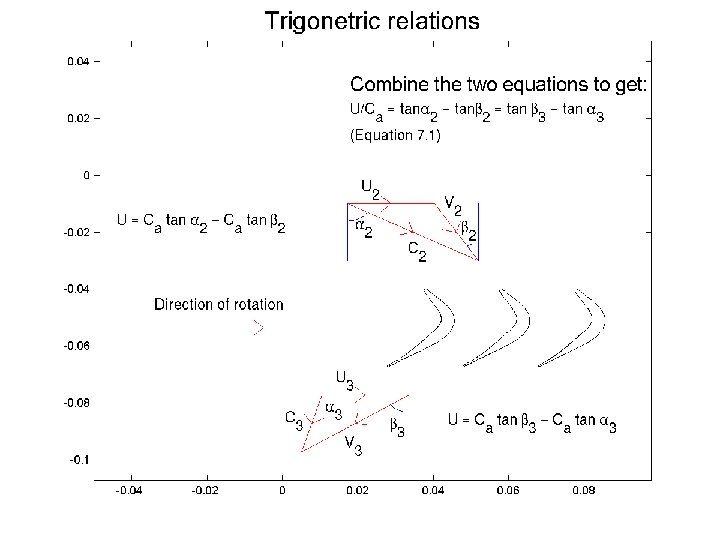
Chalmers University of Technology can be related to the blade angles! Plugging in results in definition of => The parameter quantifies relative amount of ”expansion” in rotor. Thus, equation 7. 7 relates blade angles to the relative amount of expansion. Aircraft turbine designs are typically 50% degree of reaction designs.

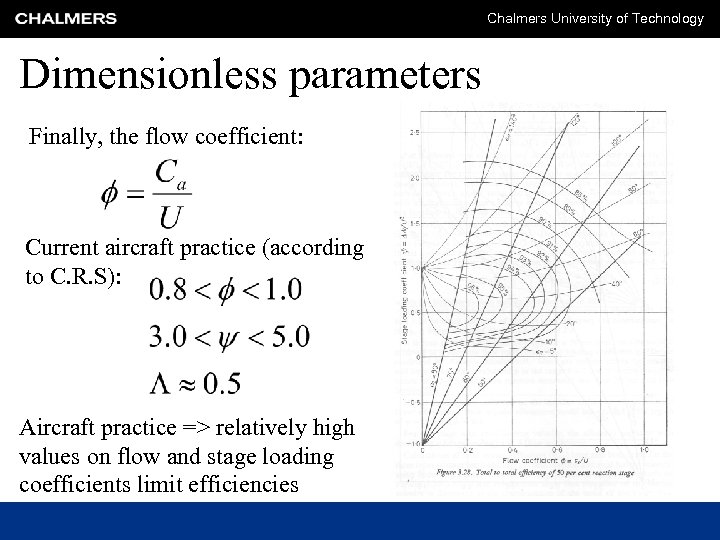Chalmers University of Technology Dimensionless parameters Finally, the flow coefficient: Current aircraft practice (according to C. R. S): Aircraft practice => relatively high values on flow and stage loading coefficients limit efficiencies

Chalmers University of Technology Dimensionless parameters Using the flow coefficient in 7. 6 and 7. 7 we obtain: The above equations and 7. 1 can be used to obtain the gas and blade angles as a function of the dimensionless parameters

Chalmers University of Technology Two simple homework exercises • Exercise: show that the velocity triangles become symmetric for = 0. 5. Hint combine 7. 1 and 7. 9 • Exercise: use the “current aircraft practice” rules to derive bounds for what would be considered conventional aircraft turbine designs. What will be the range for 3? Assume = 0. 5.

Chalmers University of Technology Turbine loss coefficients: Nozzle (stator) loss coefficients: Nozzle (rotor) loss coefficients:

Chalmers University of Technology Problem 7. 1

Chalmers University of Technology 3 D design - vortex theory • U varies with radius • Cw velocity component at stator exit => static pressure increases with radius => higher C 2 velocity at root • Twist blades to take changing gas angles into account – Vortex blading 3 D optimized blading (design beyond free vortex design)

Chalmers University of Technology 3 D design in steam turbines • Keep blade angles from root to tip (unless rt/rr high) • Cut cost • Rankine cycle relatively insensitive to component losses

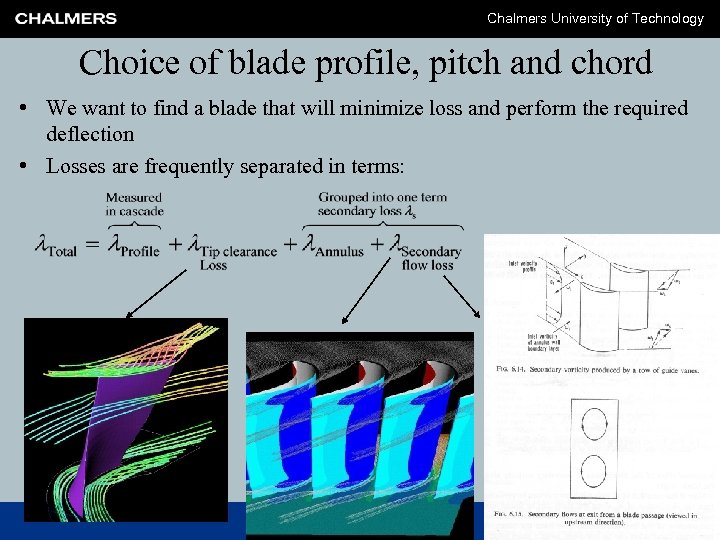Chalmers University of Technology Choice of blade profile, pitch and chord • We want to find a blade that will minimize loss and perform the required deflection • Losses are frequently separated in terms:

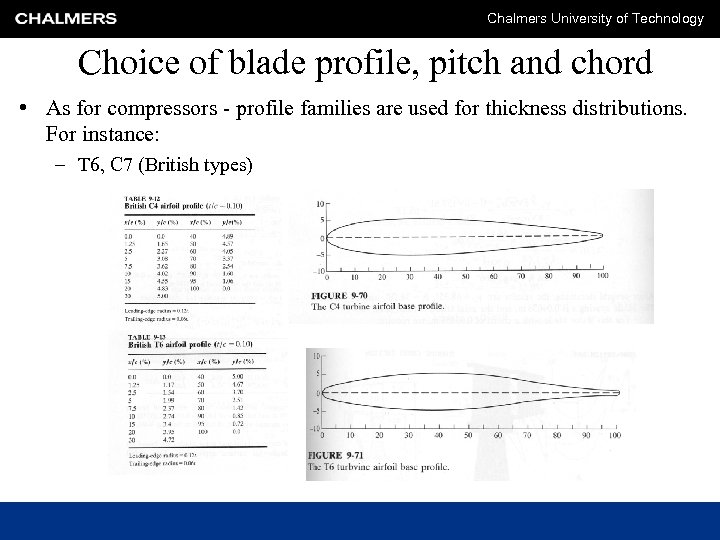Chalmers University of Technology Choice of blade profile, pitch and chord • As for compressors - profile families are used for thickness distributions. For instance: – T 6, C 7 (British types)

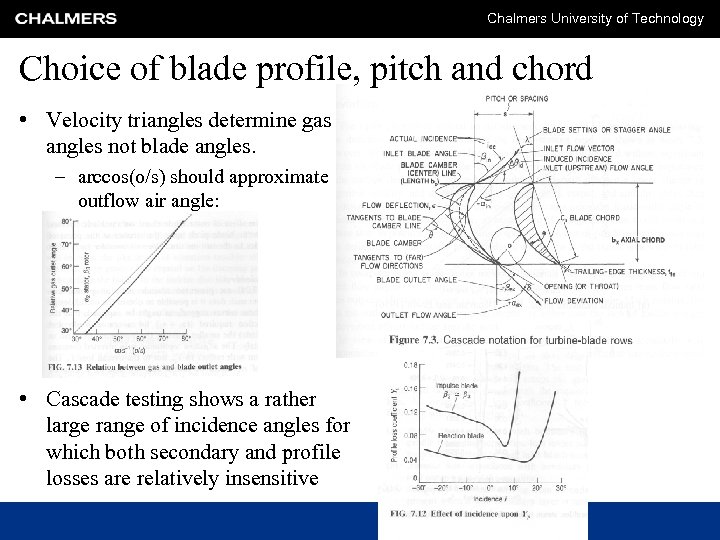Chalmers University of Technology Choice of blade profile, pitch and chord • Velocity triangles determine gas angles not blade angles. – arccos(o/s) should approximate outflow air angle: • Cascade testing shows a rather large range of incidence angles for which both secondary and profile losses are relatively insensitive

Chalmers University of Technology Choice of blade profile, pitch and chord • Selection of pitch chord: – Blade loss must be minimized (the greater the required deflection the smaller is the optimum s/c - with respect to λProfile loss) – Aspect ratio h/c. Not critical. Too low value => secondary flow and tip clearence effects in large proportion. Too high => vibration problems likely. 3 -4 typical. h/c < 1 too low. – Effect on root fixing • Pitch must not be too small to allow safe fixing to turbine disc rim