Challenges in Combinatorial Scientific Computing John R Gilbert

Challenges in Combinatorial Scientific Computing John R. Gilbert University of California, Santa Barbara Georgia Tech CSE Colloquium March 12, 2010 1 Support: NSF, DARPA, SGI

Combinatorial Scientific Computing “I observed that most of the coefficients in our matrices were zero; i. e. , the nonzeros were ‘sparse’ in the matrix, and that typically the triangular matrices associated with the forward and back solution provided by Gaussian elimination would remain sparse if pivot elements were chosen with care” - Harry Markowitz, describing the 1950 s work on portfolio theory that won the 1990 Nobel Prize for Economics 2

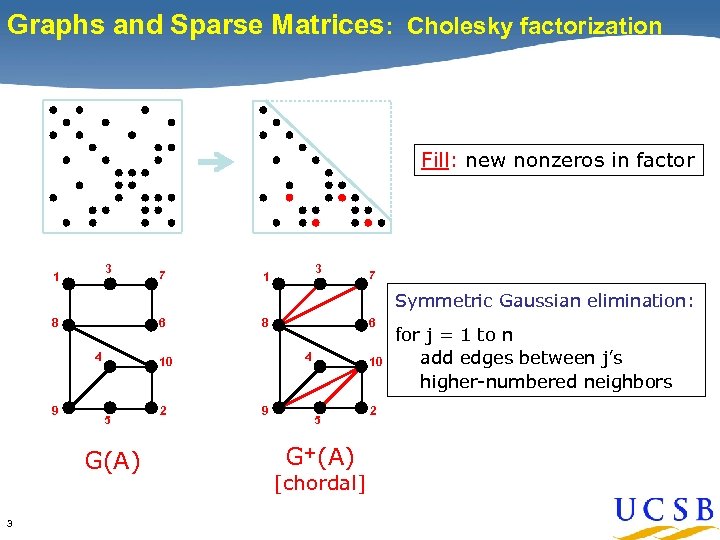
Graphs and Sparse Matrices: Cholesky factorization Fill: new nonzeros in factor 3 1 7 Symmetric Gaussian elimination: 6 8 4 9 G(A) 3 4 10 5 2 6 8 9 10 5 G+(A) [chordal] 2 for j = 1 to n add edges between j’s higher-numbered neighbors

Large graphs are everywhere… • Internet structure • Social interactions WWW snapshot, courtesy Y. Hyun 4 • Scientific datasets: biological, chemical, cosmological, ecological, … Yeast protein interaction network, courtesy H. Jeong

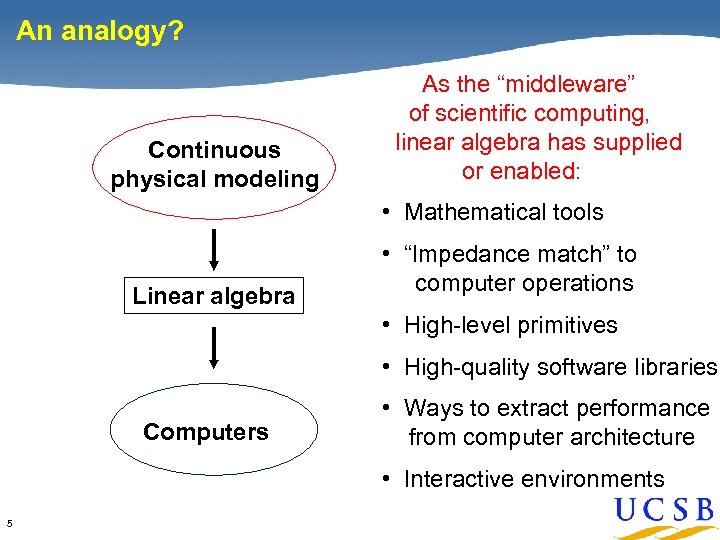
An analogy? Continuous physical modeling As the “middleware” of scientific computing, linear algebra has supplied or enabled: • Mathematical tools Linear algebra • “Impedance match” to computer operations • High-level primitives • High-quality software libraries Computers • Ways to extract performance from computer architecture • Interactive environments 5

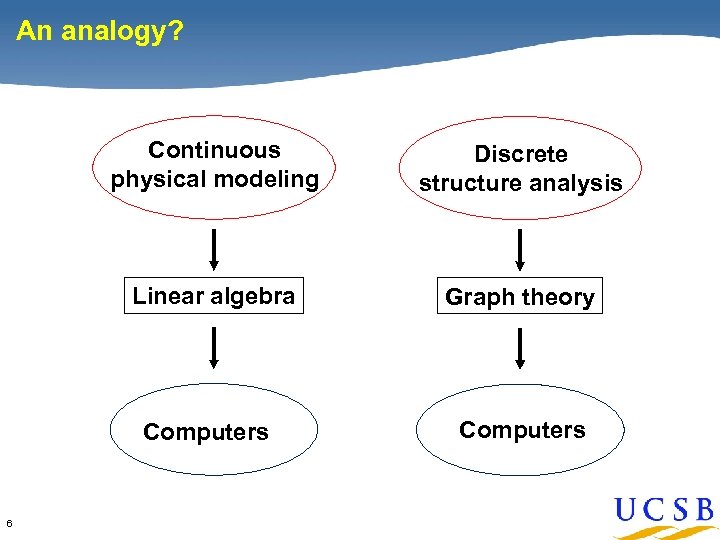
An analogy? Continuous physical modeling Discrete structure analysis Linear algebra Graph theory Computers 6 Computers

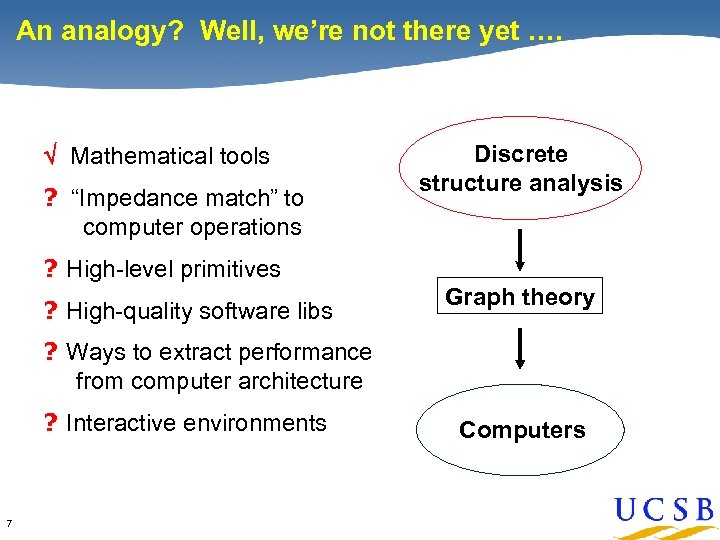
An analogy? Well, we’re not there yet …. Mathematical tools ? “Impedance match” to computer operations Discrete structure analysis ? High-level primitives ? High-quality software libs Graph theory ? Ways to extract performance from computer architecture ? Interactive environments 7 Computers

All-Pairs Shortest Paths on a GPU [Buluc et al. ] Based on R-Kleene algorithm Well suited for GPU architecture: • In-place computation => low memory bandwidth • Few, large Mat. Mul calls => low GPU dispatch overhead A A D B + is “min”, A = A*; D × is “add” % recursive call • Recursion stack on host CPU, B = AB; C = CA; not on multicore GPU D = D + CB; • Careful tuning of GPU code • 9 B C C Fast matrix-multiply kernel D = D*; % recursive call B = BD; C = DC; A = A + BC;

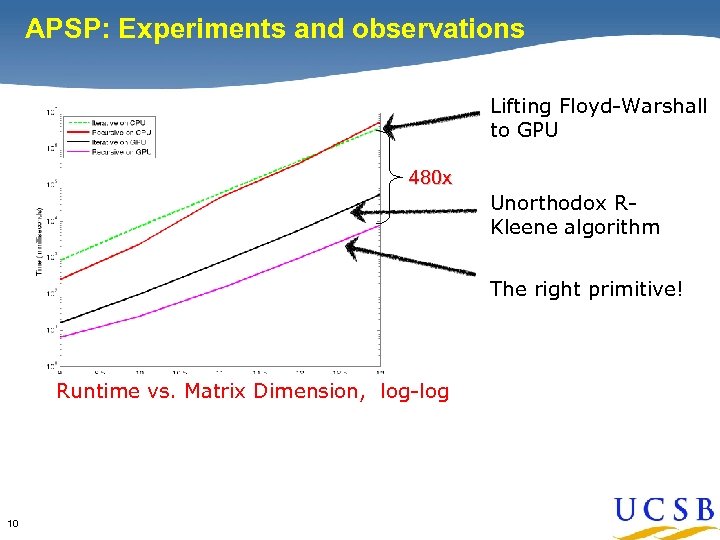
APSP: Experiments and observations The Case for Primitives Lifting Floyd-Warshall to GPU 480 x Unorthodox RKleene algorithm The right primitive! Runtime vs. Matrix Dimension, log-log 10

APSP: Experiments and observations The Case for Primitives Lifting Floyd-Warshall to GPU 480 x Unorthodox RKleene algorithm The right primitive! Runtime vs. Matrix Dimension, log-log • High performance is achievable but not simple • Carefully chosen and optimized primitives are key • Matching the architecture and the algorithm is key 11

Landscape connectivity modeling [Shah et al. ] • • Pumas in southern California: 12 million nodes, < 1 hour • 13 Habitat quality, gene flow, corridor identification, conservation planning Targeting larger problems: Yellowstone-to-Yukon corridor Figures courtesy of Brad Mc. Rae, NCEAS

Coloring for parallel nonsymmetric preconditioning [Aggarwal et al. ] 263 million DOF • • • 14 Level set method for multiphase interface problems in 3 D. Nonsymmetric-structure, second-order-accurate octree discretization. Bi. CGSTAB preconditioned by parallel triangular solves.

NMF traffic analysis results [Karpinski et al. ] 15

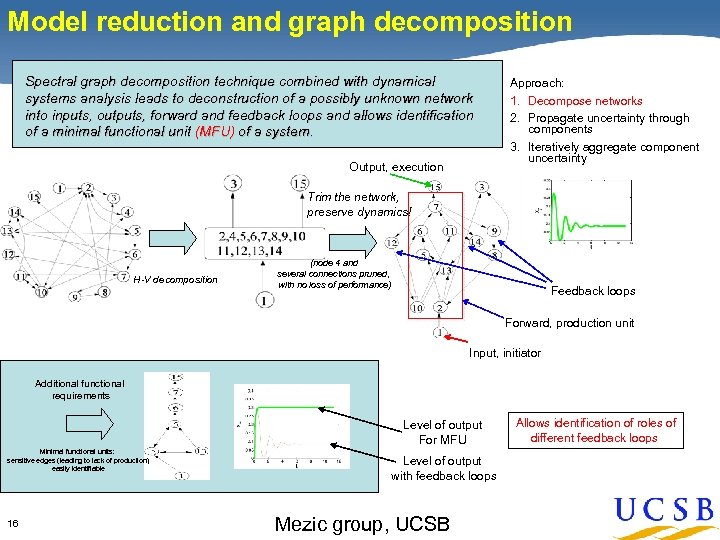
Model reduction and graph decomposition Spectral graph decomposition technique combined with dynamical systems analysis leads to deconstruction of a possibly unknown network into inputs, outputs, forward and feedback loops and allows identification of a minimal functional unit (MFU) of a system. Output, execution Approach: 1. Decompose networks 2. Propagate uncertainty through components 3. Iteratively aggregate component uncertainty Trim the network, preserve dynamics! H-V decomposition (node 4 and several connections pruned, with no loss of performance) Feedback loops Forward, production unit Input, initiator Additional functional requirements Level of output For MFU Minimal functional units: sensitive edges (leading to lack of production) easily identifiable 16 Level of output with feedback loops Mezic group, UCSB Allows identification of roles of different feedback loops

Horizontal - vertical decomposition [Mezic et al. ] 1 level 4 9 8 2 3 4 5 6 7 8 9 1 2 6 level 3 3 7 4 5 level 2 2 3 4 5 6 7 8 level 1 1 9 • Strongly connected components, ordered by levels of DAG • Linear-time sequentially; no work/span efficient parallel algorithms known • … but we don’t want an exact algorithm anyway; edges are probabilities, and the application is a kind of statistical model reduction … 17

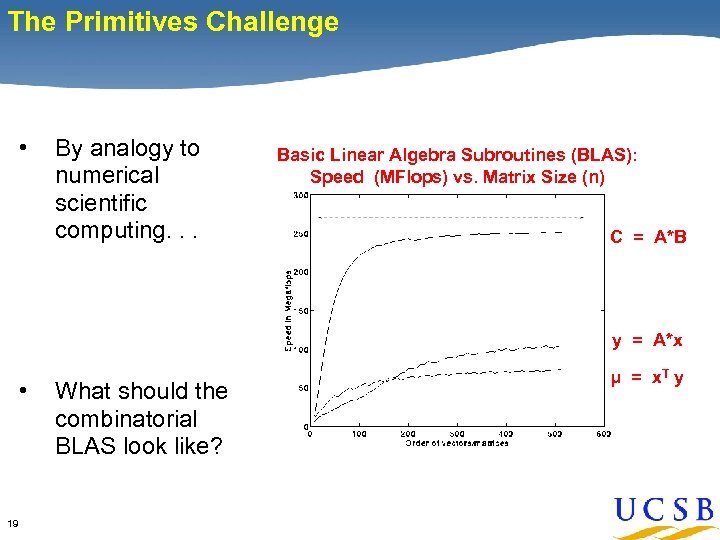
The Primitives Challenge • By analogy to numerical scientific computing. . . Basic Linear Algebra Subroutines (BLAS): Speed (MFlops) vs. Matrix Size (n) C = A*B y = A*x • 19 What should the combinatorial BLAS look like? μ = x. T y

Primitives should… • • Have broad scope but fit into a concise framework • Allow programming at the appropriate level of abstraction and granularity • Scale seamlessly from desktop to supercomputer • 20 Supply a common notation to express computations Hide architecture-specific details from users

Frameworks for graph primitives Many possibilities; none completely satisfactory; little work on common frameworks or interoperability. • • Visitor-based, multithreaded: MTGL • Heterogeneous, tuned kernels: SNAP • Scan-based vectorized: NESL • Map-reduce: lots of visibility • 21 Visitor-based, distributed-memory: PBGL Sparse array-based: Matlab *PKDT, CBLAS

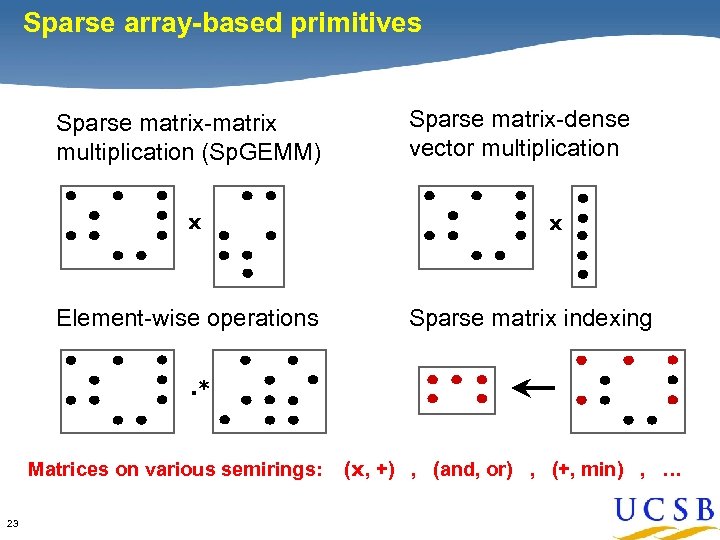
Sparse array-based primitives Identification of Primitives Sparse matrix-matrix multiplication (Sp. GEMM) x Element-wise operations Sparse matrix-dense vector multiplication x Sparse matrix indexing . * Matrices on various semirings: 23 (x, +) , (and, or) , (+, min) , …

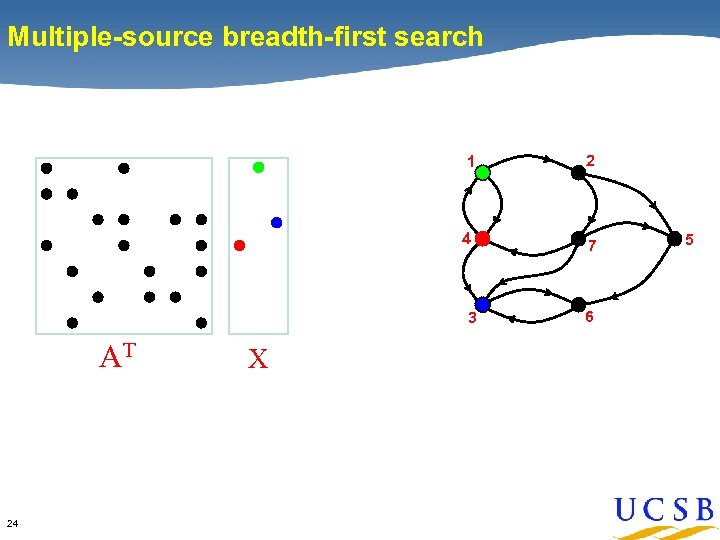
Multiple-source breadth-first search 1 2 4 7 3 AT 24 X 6 5

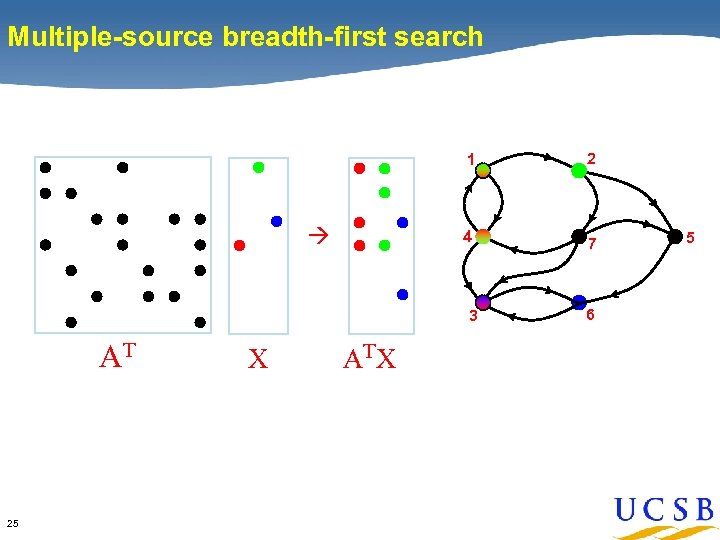
Multiple-source breadth-first search 1 4 2 7 3 AT 25 X AT X 6 5

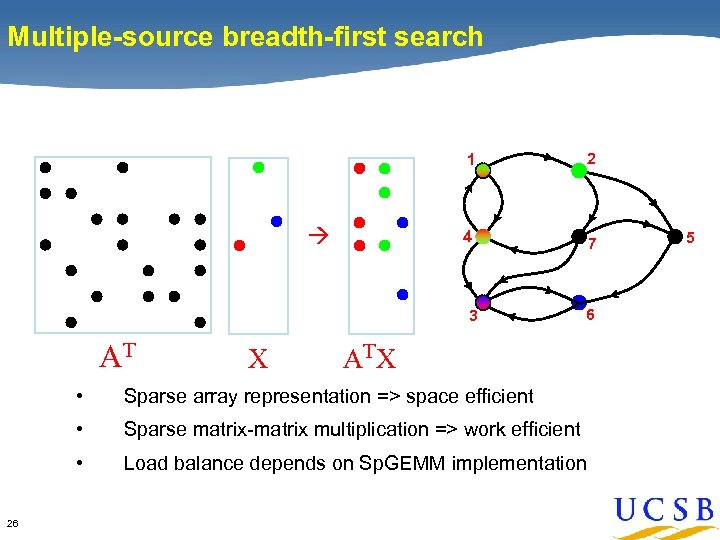
Multiple-source breadth-first search 1 4 2 7 3 AT X 6 AT X • • Sparse matrix-matrix multiplication => work efficient • 26 Sparse array representation => space efficient Load balance depends on Sp. GEMM implementation 5

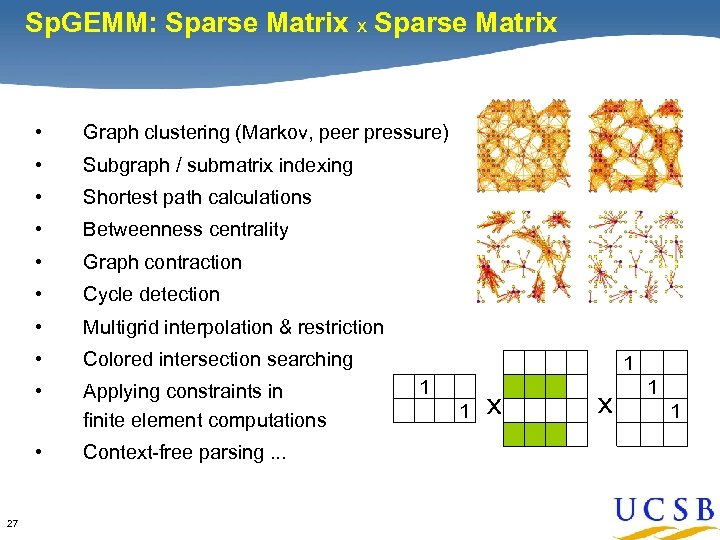
Sp. GEMM: Sparse Matrix x Sparse Matrix Why focus on Sp. GEMM? • • Subgraph / submatrix indexing • Shortest path calculations • Betweenness centrality • Graph contraction • Cycle detection • Multigrid interpolation & restriction • Colored intersection searching • Applying constraints in finite element computations • 27 Graph clustering (Markov, peer pressure) Context-free parsing. . . 1 1 1 x x 1 1

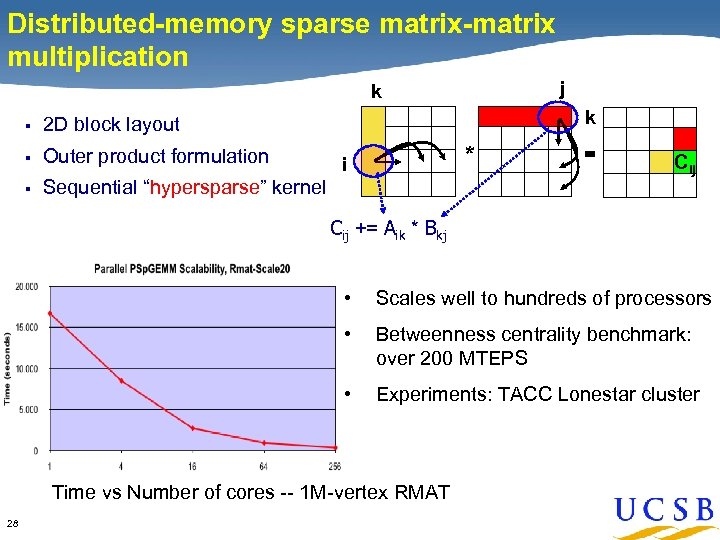
Distributed-memory sparse matrix-matrix multiplication j k § § Outer product formulation § k 2 D block layout Sequential “hypersparse” kernel * i = Cij += Aik * Bkj • Scales well to hundreds of processors • Betweenness centrality benchmark: over 200 MTEPS • Experiments: TACC Lonestar cluster Time vs Number of cores -- 1 M-vertex RMAT 28

$The Combinatorial BLAS: Example of use Applications and Algorithms Betweenness Centrality (BC) What fraction$

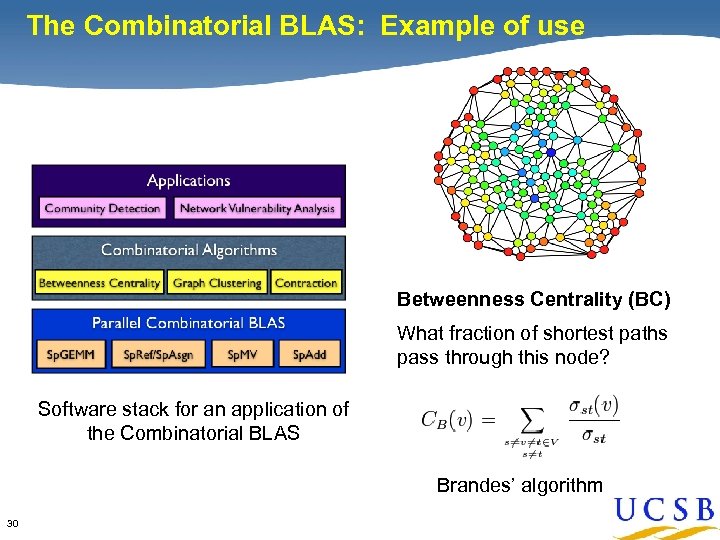
The Combinatorial BLAS: Example of use Applications and Algorithms Betweenness Centrality (BC) What fraction of shortest paths pass through this node? Software stack for an application of the Combinatorial BLAS Brandes’ algorithm 30

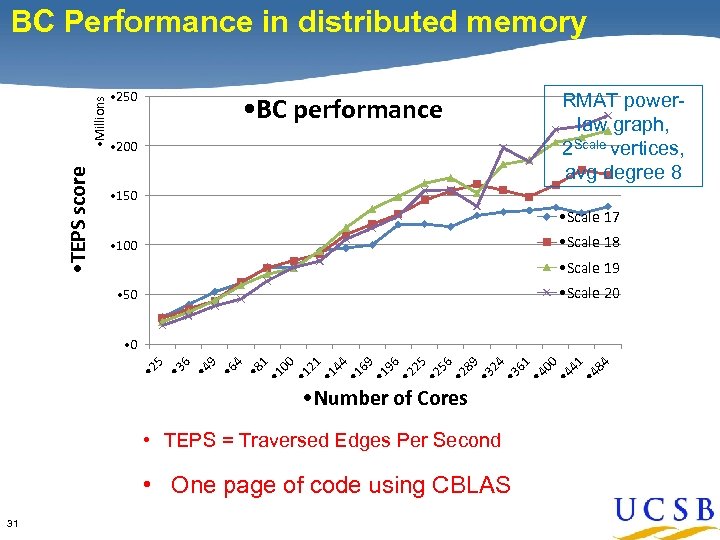
• TEPS score • Millions BC Performance in distributed memory • 250 • BC performance • 200 RMAT powerlaw graph, 2 Scale vertices, avg degree 8 • 150 • Scale 17 • Scale 18 • 100 • Scale 19 • Scale 20 • 50 • 8 1 • 1 00 • 1 21 • 1 44 • 1 69 • 1 96 • 2 25 • 2 56 • 2 89 • 3 24 • 3 61 • 4 00 • 4 41 • 4 84 4 • 6 9 • 4 6 • 3 • 2 5 • 0 • Number of Cores • TEPS = Traversed Edges Per Second • One page of code using CBLAS 31

The Architecture & Algorithms Challenge Two Nvidia 8800 GPUs > 1 TFLOPS Oak Ridge / Cray Jaguar > 1. 75 PFLOPS § Parallelism is no longer optional… § … in every part of a computation. 33 Intel 80 core chip > 1 TFLOPS

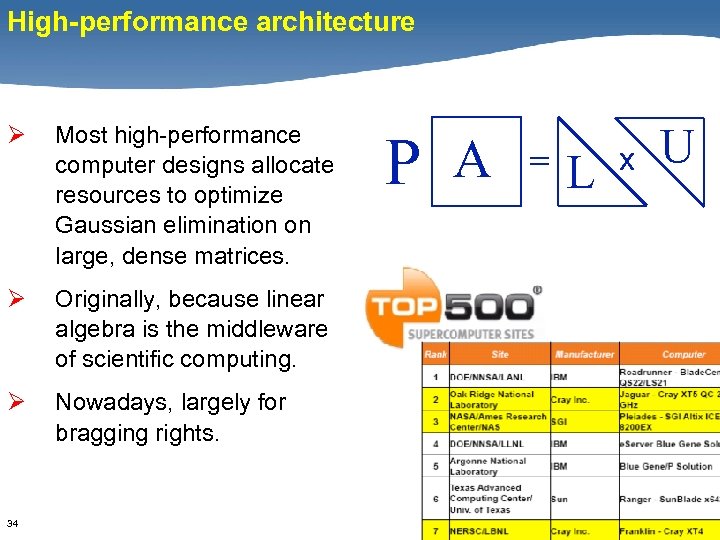
High-performance architecture Ø Most high-performance computer designs allocate resources to optimize Gaussian elimination on large, dense matrices. Ø Originally, because linear algebra is the middleware of scientific computing. Ø Nowadays, largely for bragging rights. 34 P A = L x U

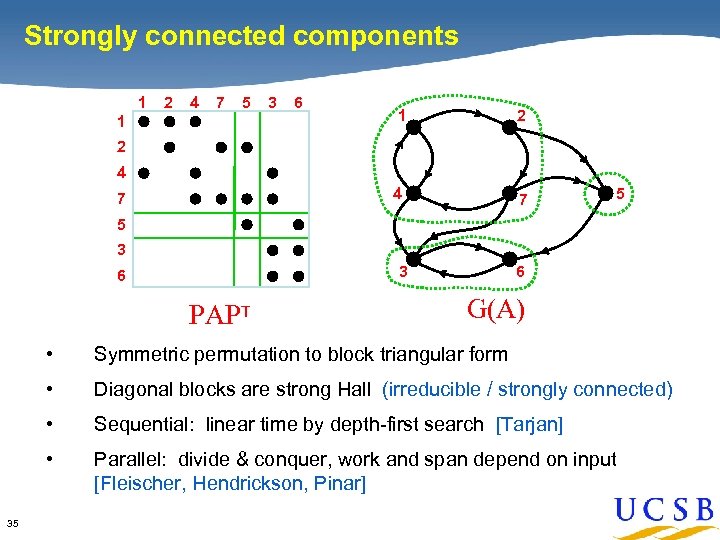
Strongly connected components 1 2 4 7 5 3 6 1 2 4 1 7 2 4 7 5 5 3 6 PAPT G(A) • • Diagonal blocks are strong Hall (irreducible / strongly connected) • Sequential: linear time by depth-first search [Tarjan] • 35 Symmetric permutation to block triangular form Parallel: divide & conquer, work and span depend on input [Fleischer, Hendrickson, Pinar]

The memory wall blues Ø Most of memory is hundreds or thousands of cycles away from the processor that wants it. Ø You can buy more bandwidth, but you can’t buy less latency. (Speed of light, for one thing. ) 36

The memory wall blues Ø Most of memory is hundreds or thousands of cycles away from the processor that wants it. Ø You can buy more bandwidth, but you can’t buy less latency. (Speed of light, for one thing. ) Ø You can hide latency with either locality or parallelism. 37

The memory wall blues Ø Most of memory is hundreds or thousands of cycles away from the processor that wants it. Ø You can buy more bandwidth, but you can’t buy less latency. (Speed of light, for one thing. ) Ø You can hide latency with either locality or parallelism. Ø Most interesting graph problems have lousy locality. Ø Thus the algorithms need even more parallelism! 38

Architectural impact on algorithms Matrix multiplication: C = A * B C = 0; for i = 1 : n for j = 1 : n for k = 1 : n C(i, j) = C(i, j) + A(i, k) * B(k, j); O(n 3) operations 39

Architectural impact on algorithms Naïve 3 -loop matrix multiply [Alpern et al. , 1992]: 12000 would take 1095 years T = N 4. 7 Size 2000 took 5 days Naïve algorithm is O(N 5) time under UMH model. BLAS-3 DGEMM and recursive blocked algorithms are O(N 3). 40 Diagram from Larry Carter

The architecture & algorithms challenge Ø Ø 41 A big opportunity exists for computer architecture to influence combinatorial algorithms. (Maybe even vice versa. )

A novel architectural approach: Cray MTA / XMT • • Per-tick context switching • Uniform (sort of) memory access time • 42 Hide latency by massive multithreading But the economic case is still not completely clear.

Some Challenges 43

Features of (many) large graph applications • “Feasible” means O(n), or even less. • You can’t scan all the data. – – • you want to poke at it in various ways maybe interactively. Multiple simultaneous queries to the same graph – maybe to differently filtered subgraphs – throughput and response time are both important. • • 44 Benchmark data sets are a big challenge! Sometimes, think of data not as a finite object but as a statistical sample of an infinite process.

Productivity Raw performance isn’t always the only criterion. Other factors include: • • Interactive response for data exploration and viz • Rapid prototyping • 45 Seamless scaling from desktop to HPC Just plain programmability

The Education Challenge Ø How do you teach this stuff? Ø Where do you go to take courses in Ø Graph algorithms … Ø … on massive data sets … Ø … in the presence of uncertainty … Ø … analyzed on parallel computers … Ø … applied to a domain science? 46

Final thoughts • • Linear algebra and combinatorics can support each other in computation as well as in theory. • A big opportunity exists for computer architecture to influence combinatorial algorithms. • 47 Combinatorial algorithms are pervasive in scientific computing and will become more so. This is a great time to be doing research in combinatorial scientific computing!

Extra Slides 48

A few research questions in high-performance combinatorial computing Ø Primitives for computation on graphs and other discrete structures – What is the right set of primitives? – What is the API? – How do you get performance on a wide range of platforms? Ø Tools and libraries: How will results be used by nonspecialists? Ø Building useful reference data sets, data generators, and benchmarks Ø How can computer architecture influence combinatorial algorithms? Ø Computing global properties of networks – – Connectivity, robustness, spectral properties – 49 Not just density, diameter, degree distribution, clustering coeff Sensitivity analysis, stochastic and dynamic settings

Sp. GEMM Details 50

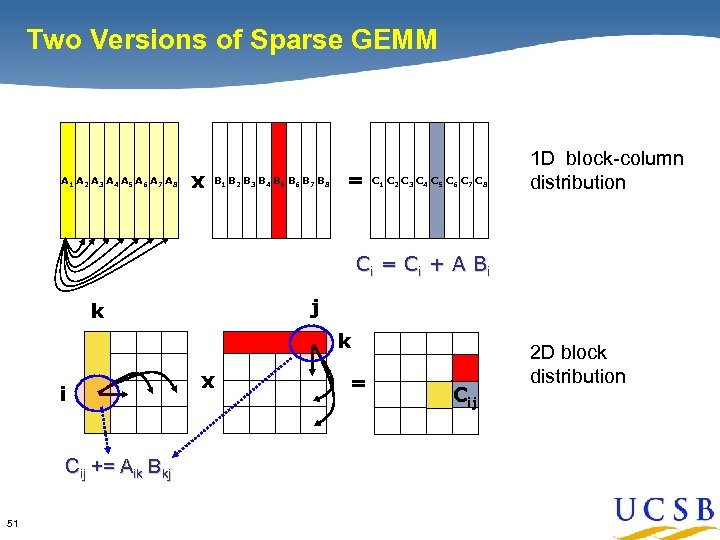
Two Versions of Sparse GEMM A 1 A 2 A 3 A 4 A 5 A 6 A 7 A 8 x B 1 B 2 B 3 B 4 B 5 B 6 B 7 B 8 = C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 1 D block-column distribution Ci = C i + A B i j k k i Cij += Aik Bkj 51 x = Cij 2 D block distribution

Modeled bounds on speedup, sparse 1 -D & 2 -D algorithm 1 -D algorithm N P N • 1 -D algorithms do not scale beyond 40 x • Break-even point is around 50 processors 52 P

Submatrices are hypersparse (i. e. nnz << n) nnz’ = blocks Average of c nonzeros per column Total Storage: blocks • An algorithm whose complexity depends on matrix dimension n is asymptotically too wasteful. 53

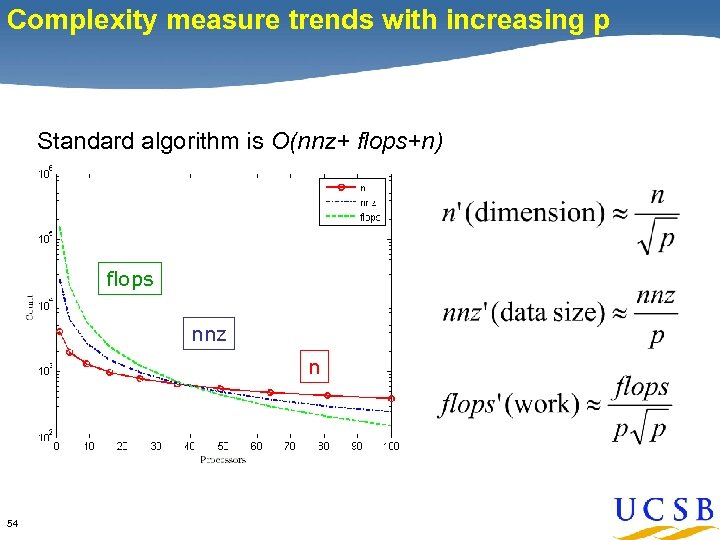
Complexity measure trends with increasing p Standard algorithm is O(nnz+ flops+n) flops nnz n 54

Sequential Kernel [IPDPS 2008] • Strictly O(nnz) data structure • Complexity independent of matrix dimension • Outer-product formulation with multi-way merging • Scalable in terms of the amount of work it performs. • X 5 55

Parallel Interactive Tools: Star-P & Knowledge Discovery Toolbox 56

Star-P A = rand(4000*p, 4000*p); x = randn(4000*p, 1); y = zeros(size(x)); while norm(x-y) / norm(x) > 1 e-11 y = x; x = A*x; x = x / norm(x); end; 57

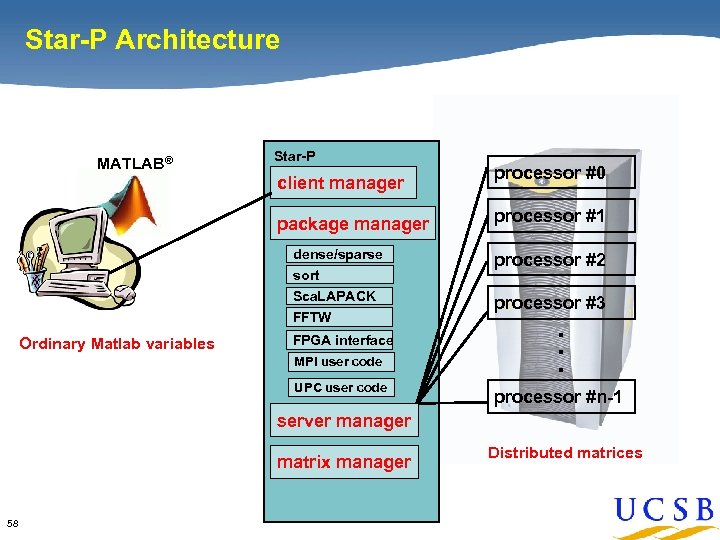
Star-P Architecture MATLAB® Star-P client manager package manager processor #0 processor #1 processor #2 Sca. LAPACK processor #3 FFTW Ordinary Matlab variables FPGA interface MPI user code UPC user code . . . dense/sparse sort processor #n-1 server manager matrix manager 58 Distributed matrices

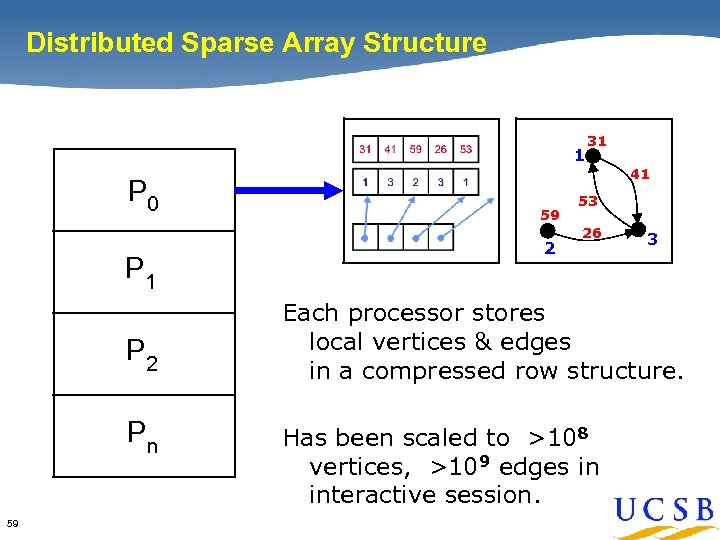
Distributed Sparse Array Structure 1 P 0 P 1 P 2 Pn 59 31 41 59 2 53 26 3 Each processor stores local vertices & edges in a compressed row structure. Has been scaled to >108 vertices, >109 edges in interactive session.

Star-P History • 1998: Matlab*P 1. 0: Edelman, Husbands, Isbell (MIT) • 2002 – 2006: Matlab*P 2. 0: MIT / UCSB / LBNL • 2004 – 2009: Interactive Supercomputing (orig. with SGI) • 2008: Many large and small Star-P installations, including – San Diego Supercomputing Center – Pittsburgh Supercomputing Center • 2009: ISC bought by Microsoft 60

KDT: A toolbox for graph analysis and pattern discovery [G, Reinhardt, Shah] Layer 1: Graph Theoretic Tools • • Global structure of graphs • Graph partitioning and clustering • Graph generators • Visualization and graphics • Scan and combining operations • 61 Graph operations Utilities

Sample application stack Computational ecology, CFD, data exploration Applications CG, Bi. CGStab, etc. + combinatorial preconditioners (AMG, Vaidya) Preconditioned Iterative Methods Graph querying & manipulation, connectivity, spanning trees, geometric partitioning, nested dissection, NNMF, . . . Graph Analysis & Pattern Toolbox Arithmetic, matrix multiplication, indexing, solvers (, eigs) Distributed Sparse Matrices 62

Landscape connectivity modeling [Shah et al. ] • • Pumas in southern California: 12 million nodes, < 1 hour • 63 Habitat quality, gene flow, corridor identification, conservation planning Targeting larger problems: Yellowstone-to-Yukon corridor Figures courtesy of Brad Mc. Rae, NCEAS