7c98c7a6e35170b9a7aee2f825053f4e.ppt
- Количество слайдов: 17

Chair of Software Engineering Reasoning about Multiple Related Abstractions with Multi. Star Stephan van Staden, Cristiano Calcagno

Introduction Broad topic: reasoning about the correctness of OO programs In particular: well-behaved invariants Data abstractions pervade OO programs: • Language constructs: classes • Concepts: account, counter, person, stack 2

Abstract Predicate Families (APF) Purpose: data abstraction E. g. d + 100 < b x. deposits = d ˄ x. balance = b APF predicate x. A(deps: d, bal: b) • Logical abstractions of data • APF predicate arguments are the only visible properties of the abstraction • Think in terms of interface and implementation. This enforces high-level reasoning • APF predicates can have different implementations in different classes • Inheritance-aware 3

Related abstractions Abstractions are often related: x. A(deps: d, bal: b) x. C(cnt: d) * x. R(bal: b) Possible implementations: One class Client Account d: int b: int Account d: Counter b: Balance Inheritance Counter c: int Balance b: int Account 4

The opportunity Correctness of code often depends on such relationships, but the original proof system allows only to pass APF predicates around Assume library routine use_counter(x) {x. C(cnt: d)}_{x. C(cnt: d+20)} Client reasoning: {x. A(deps: d, bal: b)} x. A(deps: d, bal: b) x. C(cnt: d) * x. R(bal: b) {x. C(cnt: d) * x. R(bal: b)} use_counter(x) {x. C(cnt: d+20) * x. R(bal: b)} // Code that assumes x. A(deps: d+20, bal: b) Client infers an A-based specification for use_counter Access control & call protocols: x. A(deps: d, bal: b) x. C(cnt: d) * x. R(bal: b) 5

The problem Original APF system lacks ways to • Specify relationships among abstractions • Verify them • Reason about code that relies on them Solutions must be flexible, since a property may apply to • Instances of particular classes • A whole class hierarchy Further requirements: soundness, modularity, simplicity 6

Our approach We use two new specification mechanisms • Export clauses for properties of individual classes • Axiom clauses for properties of entire class hierarchies Export clauses • Class C contains export P • Verification checks whether P follows from the APF assumptions of C • Clients can assume P • The paper contains examples 7

Our approach Axiom clauses • Class C contains axiom l: P • C and all its subclasses must implement axiom l • Subclasses can refine (i. e. strengthen) an axiom • Clients can assume ∀x <: C P[x/Current] • Dynamic type information is not necessary to use this axiom information E. g. axiom a 1: A(deps: d, bal: b) C(cnt: d) * R(bal: b) Method body verification can use export and axiom information of all classes 8
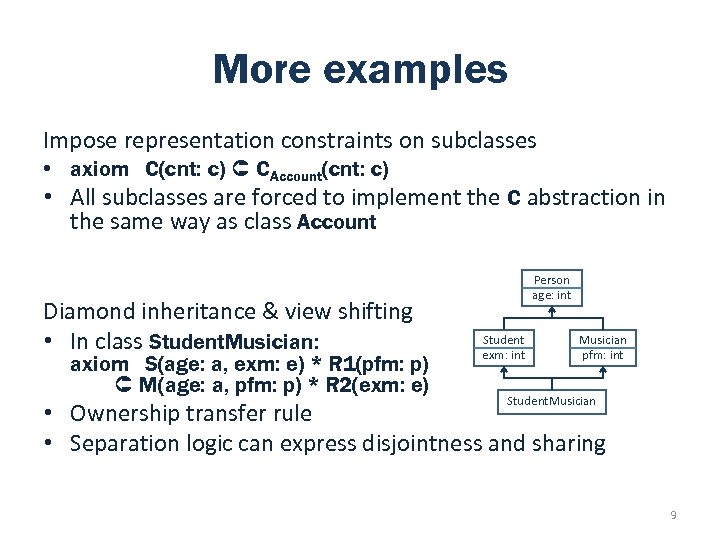
More examples Impose representation constraints on subclasses • axiom C(cnt: c) CAccount(cnt: c) • All subclasses are forced to implement the C abstraction in the same way as class Account Diamond inheritance & view shifting • In class Student. Musician: axiom S(age: a, exm: e) * R 1(pfm: p) M(age: a, pfm: p) * R 2(exm: e) Person age: int Student exm: int Musician pfm: int Student. Musician • Ownership transfer rule • Separation logic can express disjointness and sharing 9

More examples Relationships between predicate arguments • axiom A(deps: d, bal: b) d + 100 < b Properties of predicate arguments E. g. The number of deposits is non-negative • axiom A(deps: d, bal: b) 0 ≤ d Include 0 ≤ d in A predicate definitions: define x. AAccount(deps: d, bal: b) as 0 ≤ d ˄ … 10

More examples Axioms for aggregate structures that rely on other axioms Account f: Counter … Counter c: int For the Counter hierarchy: axiom cnt_non_neg: C(cnt: c) 0 ≤ c In class Account: define x. AAccount(deps: d, bal: b) as ∃y x. f ↦ y * y. C(cnt: d) * … axiom deps_nn: A(deps: d, bal: b) 0 ≤ d relies on Counter. cnt_non_neg 11

Observations Export/axiom information can be seen as well-behaved, operation-independent invariants of OO programs They are universal invariants – always hold Logical, not operational: cannot be violated by adding new methods (cf. class invariants) Idea is not to impose a methodology Only use exports and axioms where you really want them 12

Multi. Star Automated tool for verification Part of EVE, the Eiffel Verification Environment Front-end for Eiffel and back-end based on j. Star Back-end reasoning enhancements • Export and axiom clauses • Shared multiple inheritance (including interface inheritance, handling abstract classes and methods) Demonstration 13

Case study with Multi. Star Gobo data structure library’s iterator hierarchy Axiom of container hierarchy: Element. At(iter: i 1, elem: e 1, content: c 1, iters: i) * Element. At(iter: i 2, elem: e 2, content: c 1, iters: i) * Replaced(iter: i 1, value: e 2, newcontent: c 2, oldcontent: c 1, iters: i) * Replaced(iter: i 2, value: e 1, newcontent: c 3, oldcontent: c 2, iters: i) Swapped(iter 1: i 1, iter 2: i 2, newcontent: c 3, oldcontent: c 1, iters: i) 14

Other work in the paper: • Multi. Star implementation details • Formalization, proof of soundness • Related work 15

In conclusion • Two new specification mechanisms: export and axiom clauses • Simple, well-behaved and powerful • Sound proof system incorporating exports and axioms, based on separation logic and APFs • Accommodates shared multiple inheritance and interfaces • Implementation: Multi. Star verification tool 16

What about class invariants? Axioms are universal representation invariants Class invariants are properties which methods must preserve Further comparison: 17
7c98c7a6e35170b9a7aee2f825053f4e.ppt