Ch 8 Analysis Joosung Ko outline 1

Ch 8. Analysis Joosung, Ko

outline 1. 2. 3. 4. Introduction What do we want to analyze? Reachability analysis Structural analysis 1. Place invariants 2. Transition invariants 3. Automated calculation of invariants 5. Simulation 1. Example the taxi company 2. simulation using CPN Tools 6. Classical Petri nets Vs High level Petri nets 2

1. Introduction ¡ It is reasonable to make such a process model. ¡ Making a process model can help us to understand it better. ¡ A Petri-net-based process model can be used as a specification or a design of a system to be developed. ¡ A Petri-net-based process model can also be used for the analysis of a system. ¡ In this chapter, we study how to use Petri nets for the purpose of analysis.

2. What do we want to analyze? ¡ We can ask some questions to know about some systems. ¡ Two question types : qualitative and quantitative questions. ¡ If you answer, ‘yes’ or ‘no’ -> qualitative ¡ If you answer, ‘number, frequency’ -> quantitative ¡ There are two reasons to distinct these questions

3. Reachability Analysis ¡ In reachability analysis, the reachability graph of a Petri net is analyzed. ¡ With this graph of the Petri net, we can answer a number of qualitative Questions. ¡ By inspecting the reachability graph Of a high-level Petri net, we can gain insight into the occupation rates, efficiency, performance and costs of the modeled situation.

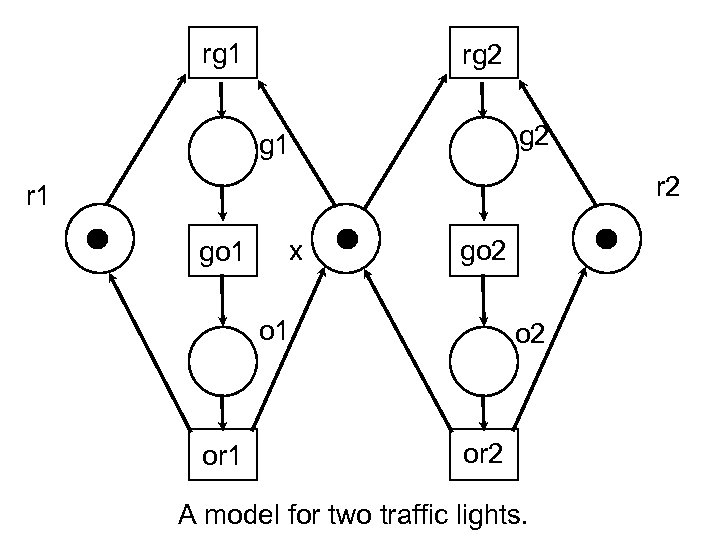rg 1 rg 2 g 1 r 2 r 1 go 1 x go 2 o 1 or 1 o 2 or 2 A model for two traffic lights.

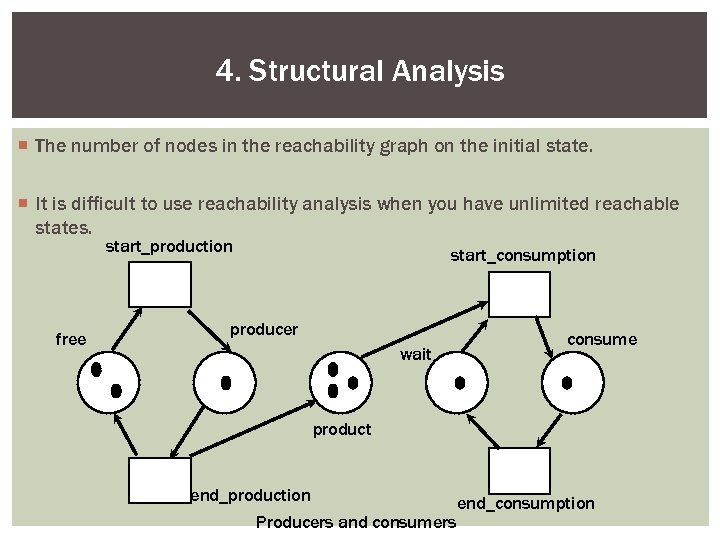4. Structural Analysis ¡ The number of nodes in the reachability graph on the initial state. ¡ It is difficult to use reachability analysis when you have unlimited reachable states. start_production free start_consumption producer wait consume product end_production Producers and consumers end_consumption

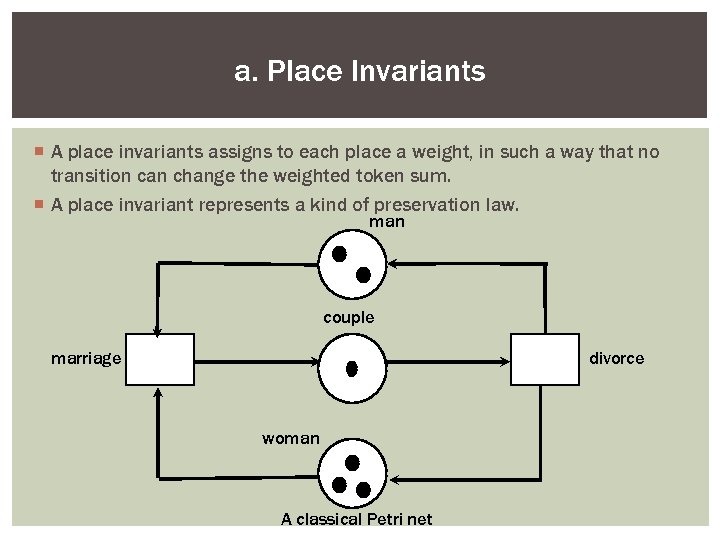a. Place Invariants ¡ A place invariants assigns to each place a weight, in such a way that no transition can change the weighted token sum. ¡ A place invariant represents a kind of preservation law. man couple marriage divorce woman A classical Petri net

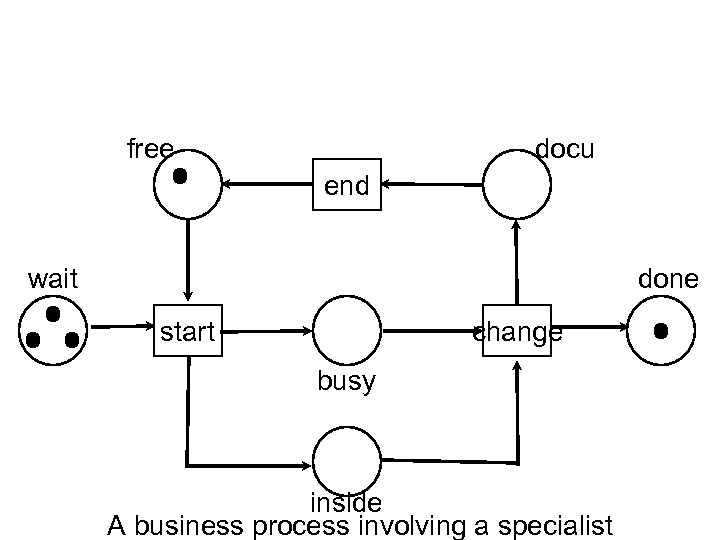free docu end wait done start change busy inside A business process involving a specialist

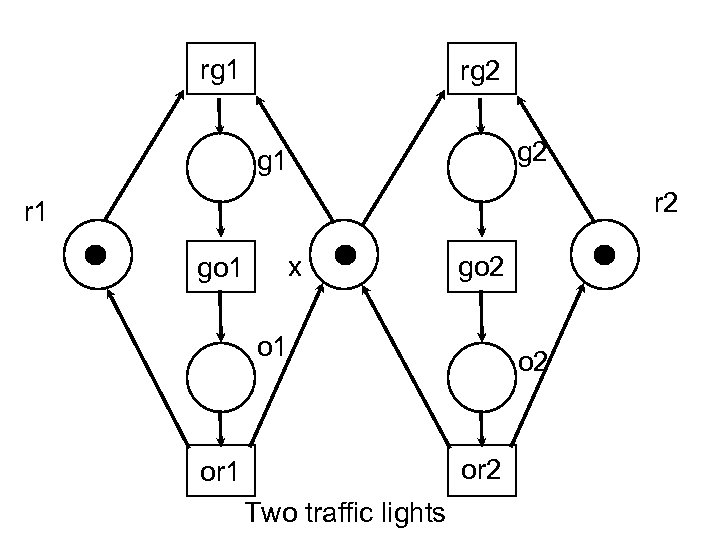rg 1 rg 2 g 1 r 2 r 1 go 1 x go 2 o 1 o 2 or 1 Two traffic lights

b. Transition invariants ¡ We use transition invariants to prove that a Petri net returns to the initial state after a certain series of firings ¡ A transition invariant assigns each transition t a weight wt in such a way that firing each transition t wt times does not change the state. The weight of a transition is not allowed to be a negative number. ¡ A transition invariant does not indicate in which order the transition should fire. Only the number of firings per transition is fixed. ¡ Transition invariants are the counterparts of place invariants. ¡ We can use invariants in two ways - We can verify whether previously determined properties indeed apply. - We can derive invariants and subsequently check which properties they represent.

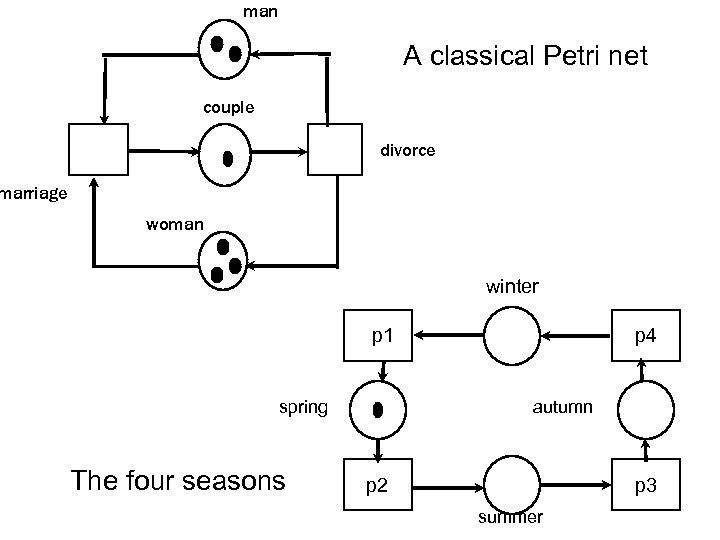man A classical Petri net couple divorce marriage woman winter p 1 spring The four seasons p 4 autumn p 2 p 3 summer

c. Automated calculation of invariants ¡ Place and transition invariants are structural techniques, and the invariants can be checked and calculated efficiently. ¡ We can simply describe how invariants can be computed. ¡ It is important to note that a Petri net can be represented by a matrix having a row for each place and a column for each T. ¡ The incidence matrix of a Petri net can be used for all kinds of analysis. ¡ It is not difficult to calculate a basis and there are many techniques to obtain the most interesting invariants.

5. Simulation ¡ The purpose of simulation is to avoid too costly or dangerous experiments. ¡ We study the simulation in the sense of experimenting with a high-level Petri net representing processes of reality. ¡ We can run the simulation through the reachability graph. ¡ To clarify things we need to discuss the concept “probability distribution” since these are typically used to specify delays in a simulation model. ¡ During the simulation all kinds of things can be measured. ¡ To determine the reliability of the measurements, the simulation run is often divided into a number of subruns.

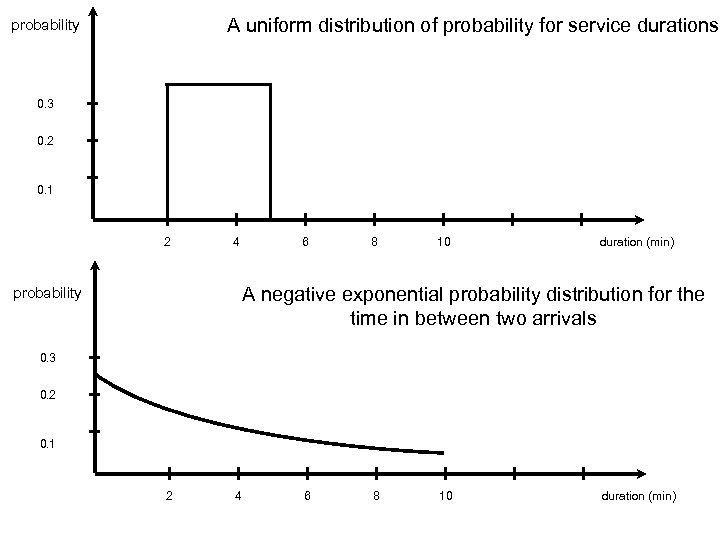A uniform distribution of probability for service durations probability 0. 3 0. 2 0. 1 2 4 6 8 10 duration (min) A negative exponential probability distribution for the time in between two arrivals probability 0. 3 0. 2 0. 1 2 4 6 8 10 duration (min)

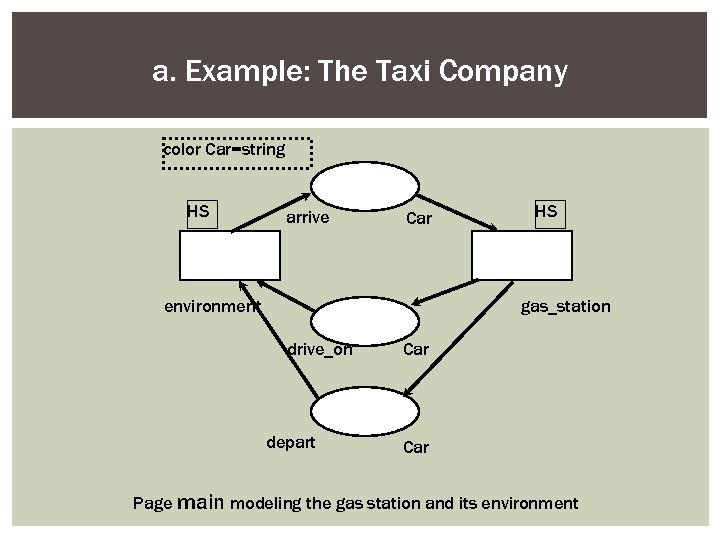a. Example: The Taxi Company color Car=string HS arrive Car environment HS gas_station drive_on depart Car Page main modeling the gas station and its environment

ln Car arrive c [len(q)<3] c put_in_queue drive_on q q^^[c] [] q q queue Queue c: : q q start () c@+uniform(2, 5) fill_up c c () pump_free Pump TCar () end color Car = string; color Pump = until; out color TCar = Car timed; color Queue = list Car; var c: Car; depart var q: Queue; fun len(q: Queue) = if q=[] then 0 else 1+len(tl(q)); c out Car drive_on Page gas_station Car

b. simulation using cpn tools

ln c arrive [len(q)<3] c Car put_in_queue q q 1 1’ 0 Queue c: : q q drive_on q q^^[c] [] queue [len(q)>=3] start () fill_up c@+discrete(2000, 5000) Car c () pump_free Pump c () 1 1’ 1@0 end c out depart out Car drive_on Car Page gas_station in CPN Tools

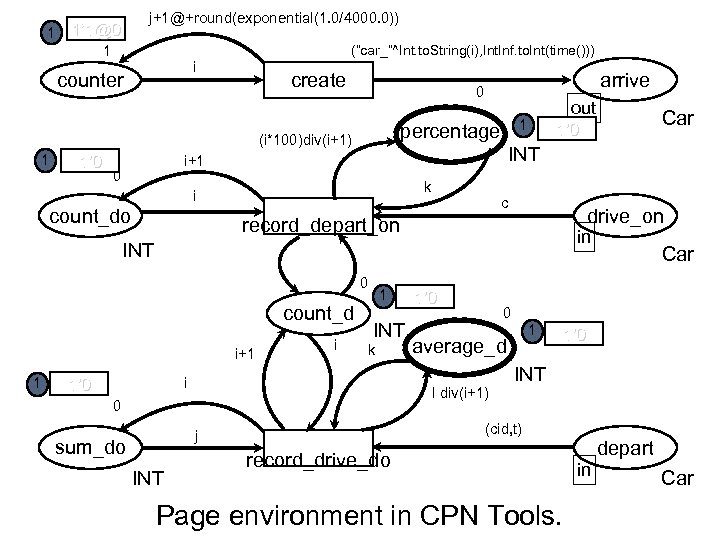j+1@+round(exponential(1. 0/4000. 0)) 1 1’ 1@0 (“car_”^Int. to. String(i), Int. Inf. to. Int(time())) 1 i counter create 1’ 0 k i count_do c drive_on record_depart_on in INT 0 count_d i+1 1 1’ 0 i 1 INT k i Car 0 1 average_d 1’ 0 INT (cid, t) j INT 1’ 0 I div(i+1) 0 sum_do Car 1’ 0 INT i+1 0 out 1 percentage (i*100)div(i+1) 1 arrive 0 record_drive_do Page environment in CPN Tools. depart in Car

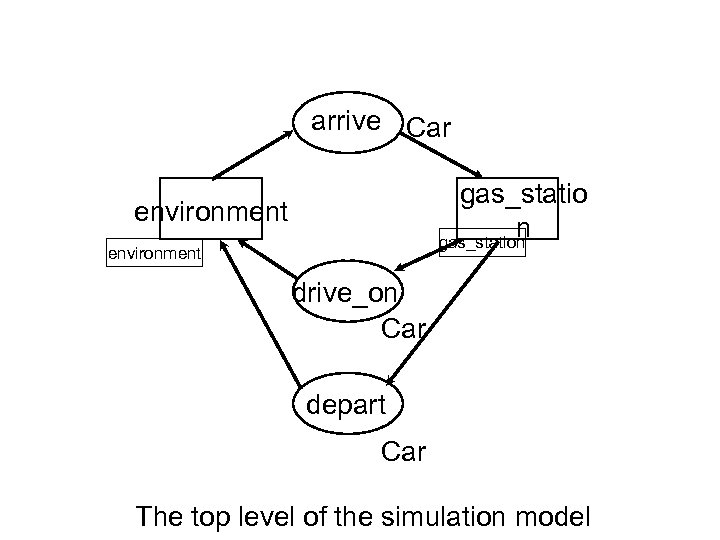arrive Car gas_statio n gas_station environment drive_on Car depart Car The top level of the simulation model

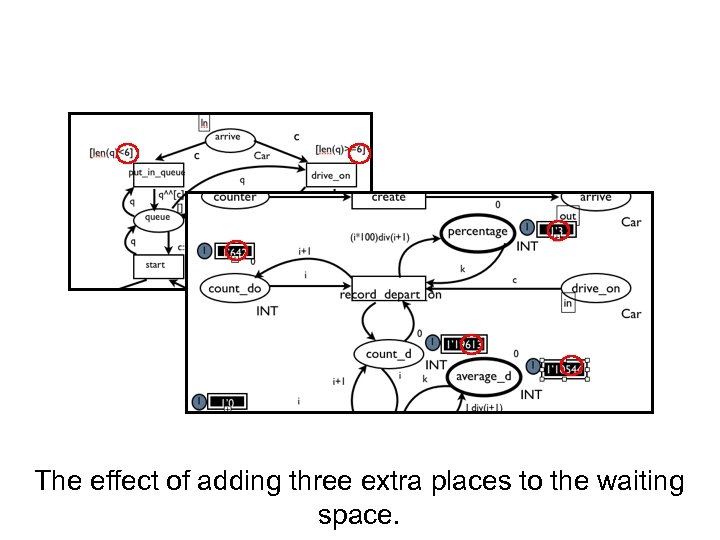The effect of adding three extra places to the waiting space.

6. classical petri nets Vs high-level petri nets ¡ The classical Petri net allows for many types of analysis and many questions are tractable ¡ To gain insight into applicability of analysis methods to high level nets we discuss each f the three extensions and their effect on analysis - The extension with color increases the expressive power of Petri nets considerably. - The extension with time adds a dimension to the Petri net - The extension with hierarchy allows for the construction of large and complex models but does not complicate analysis. 23

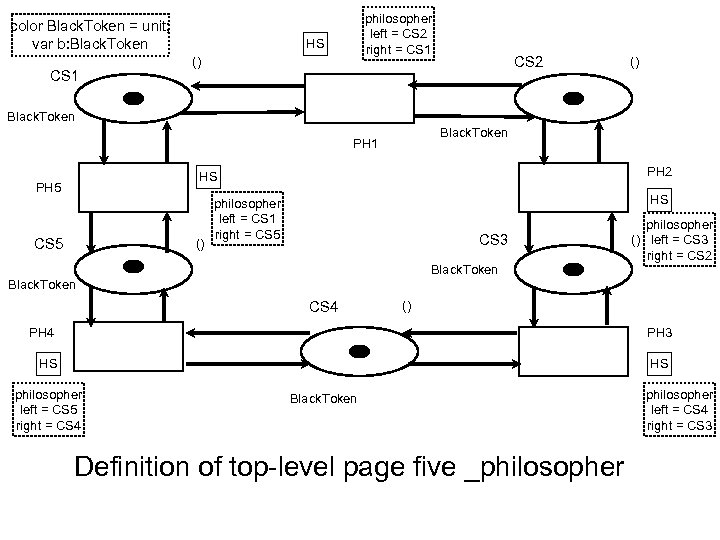color Black. Token = unit; var b: Black. Token CS 1 philosopher left = CS 2 right = CS 1 HS () CS 2 () Black. Token PH 1 PH 2 HS PH 5 CS 5 () HS philosopher left = CS 1 right = CS 5 CS 3 Black. Token philosopher () left = CS 3 right = CS 2 Black. Token CS 4 () PH 4 PH 3 HS HS philosopher left = CS 5 right = CS 4 Black. Token Definition of top-level page five _philosopher left = CS 4 right = CS 3

Thank you 25