Ch 5 Discounted Cash Flow Valuation Future

Ch. 5: Discounted Cash Flow Valuation • Future and Present Values of Multiple Cash Flows • Annuities and Perpetuities • Comparing Rates: Nominal (Stated, Quoted, APR), Periodic, Effective Annual Rates • Loan Types: Pure Discount, Interest-Only, Amortized 1

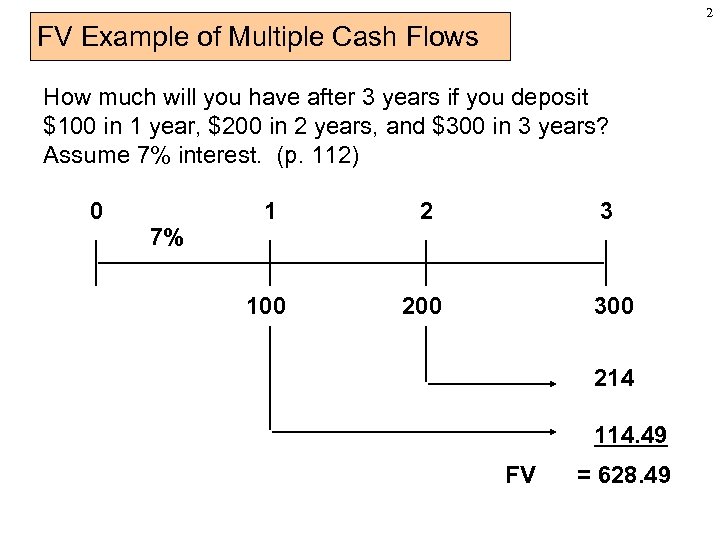2 FV Example of Multiple Cash Flows How much will you have after 3 years if you deposit $100 in 1 year, $200 in 2 years, and $300 in 3 years? Assume 7% interest. (p. 112) 0 7% 1 2 100 3 200 300 214 114. 49 FV = 628. 49

3 PV Ex. of Multiple Cash Flows What is the PV of an investment paying $200 in 1 year, $400 the next year, and $600 the next year? You can earn 12% on similar investments. (similar to p. 114) 0 178. 57 318. 88 427. 07 924. 52 = PV 2 200 12% 1 400 3 600

4 Annuities n n n An annuity is a series of equal payments at fixed intervals for a specified number of periods For an ordinary annuity the payments occur at the end of each period For an annuity due the payments occur at the beginning of each period

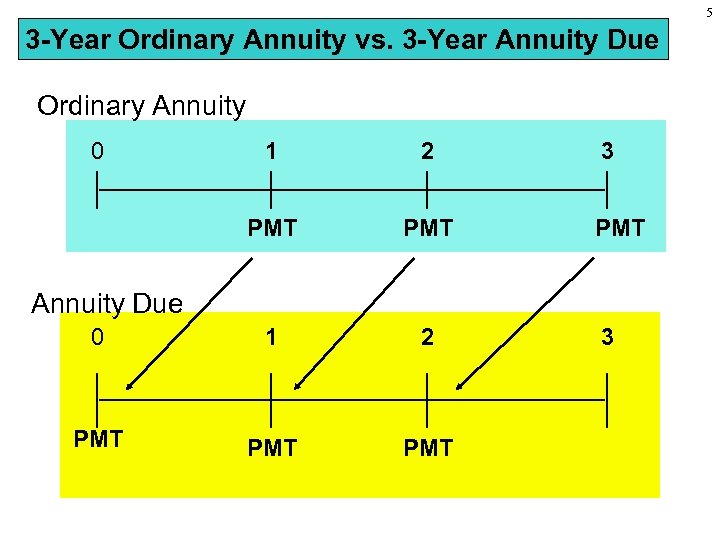5 3 -Year Ordinary Annuity vs. 3 -Year Annuity Due Ordinary Annuity 0 1 2 PMT PMT PMT 3 PMT Annuity Due 3

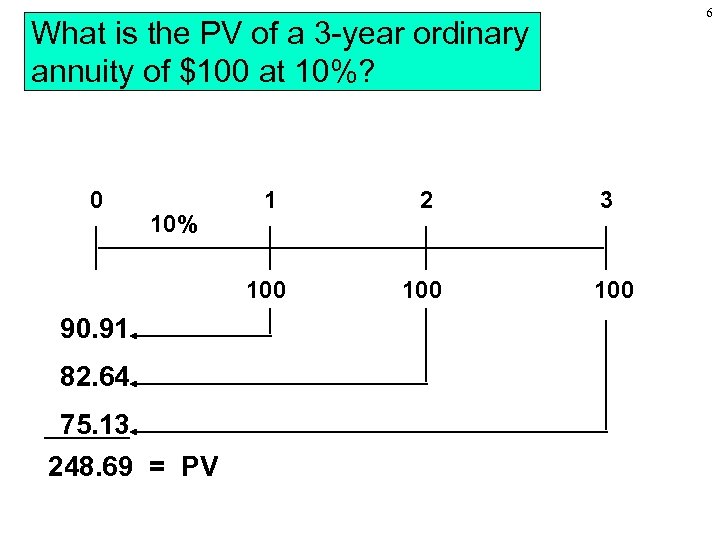6 What is the PV of a 3 -year ordinary annuity of $100 at 10%? 0 90. 91 82. 64 75. 13 248. 69 = PV 2 100 10% 1 100 3 100

7 HP-10 B Solution: INPUTS 10 N OUTPUT 3 I/YR 100 PV 0 PMT FV -248. 69 Excel FWiz: PV Table Solution: see Table A. 3: “Present value of an annuity of $1 period for t periods” Math Solution: For an annuity of $C period for t periods and interest rate r, Annuity present value = C X (1 - Present value factor)/r Formula derivation is on webpage

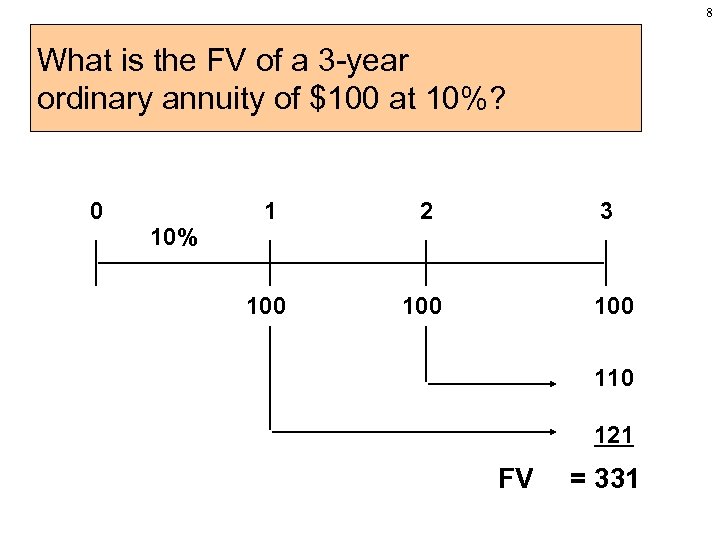8 What is the FV of a 3 -year ordinary annuity of $100 at 10%? 0 10% 1 2 100 3 100 110 121 FV = 331

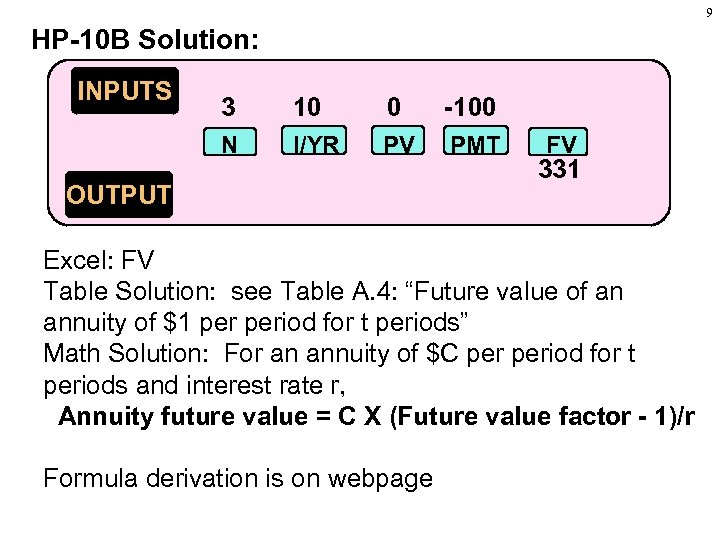9 HP-10 B Solution: INPUTS 3 10 0 -100 N I/YR PV PMT OUTPUT FV 331 Excel: FV Table Solution: see Table A. 4: “Future value of an annuity of $1 period for t periods” Math Solution: For an annuity of $C period for t periods and interest rate r, Annuity future value = C X (Future value factor - 1)/r Formula derivation is on webpage

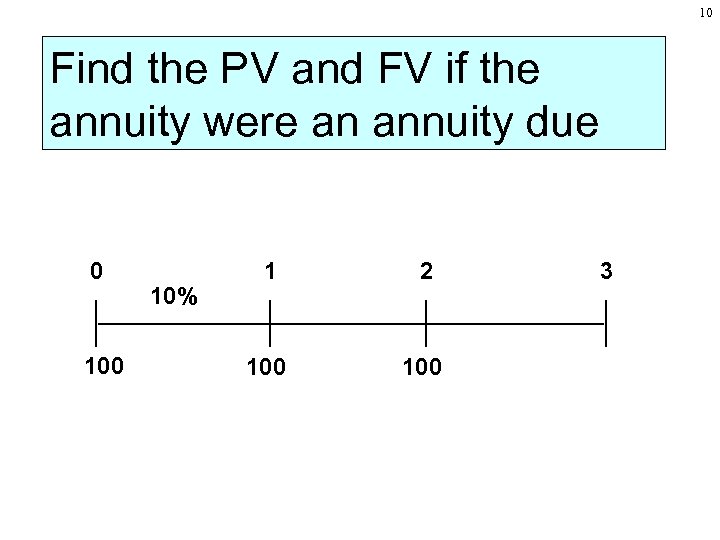10 Find the PV and FV if the annuity were an annuity due 0 10% 1 2 100 3

11 For an annuity due, switch calculator from “End” to “Begin”. Then enter variables to find PV = -$273. 55 INPUTS 3 N OUTPUT 10 I/YR PV 100 PMT 0 FV -273. 55 To find the FV of this annuity due, enter 0 for PV and solve for FV; FV = $364. 10 Be sure to finish by switching your calculator back to the “End” setting (by turning “Begin” off).

Examples • Convert a present value of $10, 000 to a fouryear ordinary annuity at 8% (Old Exam Q). • Suppose you can deposit $1, 862. 90 each January 1 from 1999 through 2002, but you need $10, 000 on January 1, 2002. What interest rate, with annual compounding, must you receive? • You have a $1000 credit-card balance, and the monthly interest rate is 1. 5%. How long will it take to pay off if you make the minimum payment of $20 per month? (pp. 121 -2) • Jackpot: annuity or lump sum? (p. 115) 12

13 Perpetuities n n A perpetuity is a stream of equal payments expected to continue forever. PV of a perpetuity = payment/interest rate Formula derivation is on webpage. Ex: What is the PV of $100 per year paid forever if the discount rate is 5%?

14 Interest Rates i. Nom = nominal rate per year (“stated, ” or “quoted”) i. Per = periodic rate (per period) EAR = EFF% = effective annual rate.

15 The Nominal Interest Rate, i. Nom • i. Nom is stated in contracts. Also known as stated or quoted rate (p. 127). Compounding periods per year (m) must also be known for calculations. APR (annual percentage rate) is the nominal rate. • Examples: 8%; Quarterly 8%, Daily interest (365 days) 8%, Daily interest (360 days) • Same as I/YR on HP-10 B

16 The Periodic Interest Rate, i. Per • Periodic rate = i. Per = i. Nom/m, where m is periods per year. m = 4 for quarterly and 360 or 365 for daily compounding. • Examples: – 8% quarterly: iper = 8/4 = 2% – 8% daily (365): iper = 8/365 = 0. 021918% • HP-10 B automatically computes the periodic rate, based on I/YR and P/YR. Most other calculators do not.

17 Will the FV of a lump sum be larger or smaller if we compound more often, holding i. Nom constant?

18 Effective Annual Rate The EAR (or EFF%) is the annual interest actually being earned. Use EAR for comparing interest rates. Ex: Beginning with $1, which quoted rate is better: a. 10% semiannually, or b. 9% quarterly? FV= PV(1 + inom/m)m FVa = 1*(1. 05)2 = 1. 1025; EAR = 10. 25% FVb = 1*(1. 0225)4 = 1. 0931; EAR = 9. 31%

19 Find EAR (= EFF%) on HP-10 B n n Ex: find EAR for a nominal rate of 10% compounded semiannually Press Clear All and check setting of P/YR Set P/YR = 2, NOM% = 10 Press EFF% to find the EAR (= 10. 25) Other calculators, Excel: either work with the periodic rate and find the annual interest actually earned, or solve the formula for EAR

20 Examples • A bank account pays 6% nominally, compounded monthly. Find the actual interest earned in a year. • You have a loan of $200, 000 for 2 years at 24% nominally, with monthly payments at the end of each month. Calculate the monthly payment. (Old Exam) • Second Bank offers 4% compounded semiannually (every 6 months) on savings deposits. Third Bank offers 4% compounded quarterly on savings deposits. Find the annual interest earned on an account at each bank. (Old Exam)

21 Given a stated rate of 10%, compare the effects of compounding annually, quarterly, monthly and daily (@ 360/yr) EARAnnual = 10% EARQ = = 10. 38% EARM = = 10. 47% EARD = = 10. 516%

22 Loan Types n n n Pure Discount: borrower receives money today and repays a single lump sum at some point in the future. Interest-Only: borrower pays interest each period and repays entire principal at some point in the future. Amortized: borrower repays part of principal plus interest each period. q business loans: interest plus a fixed amount of principal q consumer loans & mortgages: fixed payment

Examples • A borrower is willing to repay $50, 000 in five years on a pure discount loan at 12 percent annually. How much can she borrow now? • Find the cash flows for a four-year interest-only loan of $1 million at 10 percent annually. • Find the cash flows for a three-year business loan of $300, 000 at 12 percent annually amortized with 3 equal payments of principal. • You have $20, 000 for a down payment on a house. Closing costs are estimated to be 2% of loan value. Your salary is $36, 000, and the bank allows your monthly mortgage payment to be 28% of monthly income. Your mortgage is for 30 years, at 8% compounded monthly. 23

24 - continued How much will the bank lend you? What price house can you afford? Given the loan amount, how much would your monthly payment fall if interest rates drop to 7%? Recommended Practice Self-Test Problems 5. 1 - 5. 6 on pp. 134 -6 Problems 5, 7, 11, 13, 17, 19, 35, 37, 39, 41, 43, 55 on pp. 138 -43 (answers on p. 548)