CH 4751 Lecture Notes 7 -10 Erzeng Xue

CH 4751 Lecture Notes 7 -10 (Erzeng Xue) Introductory Chemistry B CH 4751 Lecture Notes 7 -10 Dr. Erzeng Xue

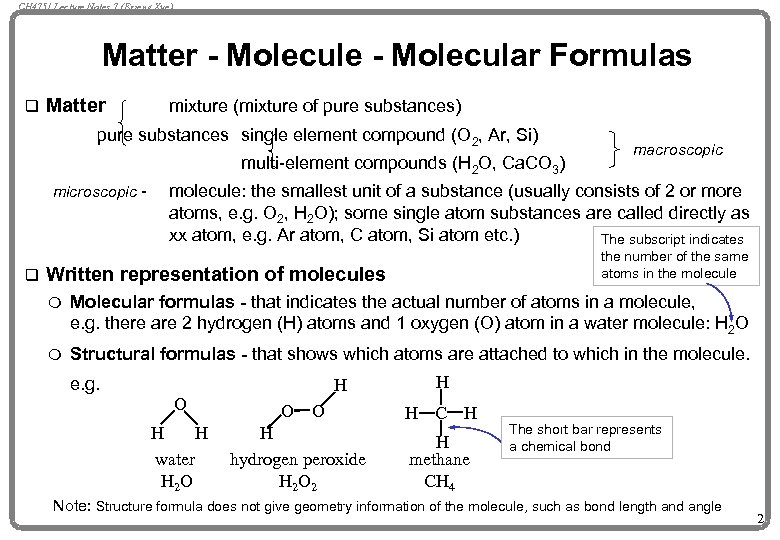CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - Molecule - Molecular Formulas q Matter mixture (mixture of pure substances) pure substances single element compound (O 2, Ar, Si) multi-element compounds (H 2 O, Ca. CO 3) microscopic - q macroscopic molecule: the smallest unit of a substance (usually consists of 2 or more atoms, e. g. O 2, H 2 O); some single atom substances are called directly as xx atom, e. g. Ar atom, C atom, Si atom etc. ) The subscript indicates the number of the same atoms in the molecule Written representation of molecules m Molecular formulas - that indicates the actual number of atoms in a molecule, e. g. there are 2 hydrogen (H) atoms and 1 oxygen (O) atom in a water molecule: H 2 O m Structural formulas - that shows which atoms are attached to which in the molecule. e. g. O H H water H 2 O H O O H hydrogen peroxide H 2 O 2 H H C H H methane CH 4 The short bar represents a chemical bond Note: Structure formula does not give geometry information of the molecule, such as bond length and angle 2

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole Counting the Atoms and Molecules q A molecule contains fixed number of atoms H 2 O, CO 2, Ca. CO 3, CH 4, C 4 H 10, etc. q In a specific chemical reaction v. A A + v. B B = v. C C + v. D D v. A, v. B, v. C and v. D are called reaction stoichiometry coefficients, which represent the ratio of number of molecules according to which the reaction proceeds. e. g. CH 4 + 2 O 2 = CO 2 + 2 H 2 O here, v. A=1, v. B=2, v. C=1 & v. D=2, which means that ONE molecule of CH 4 can react with TWO molecules of O 2, producing ONE molecule of CO 2 and TWO molecule of H 2 O. Exercise: 2 NO + O 2 = 2 NO 2 what are the values of stoichiometry coefficient? ð In the microscopic scale, the composition of a substance or a chemical reaction are quantified by the number of atoms or molecules 3

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole q In industry/lab the quantities of matter are accounted by g, tons, litre, m 3 etc e. g. we say 10 m 3 gas, 10 litres of water etc q Questions: 1) How to relate the a. m. u. of a H 2 O molecule to a daily mass scale, say, gram? 2) for the reaction: Ca. CO 3(s)=Ca. O+CO 2 - Can we say 1 kg Ca. CO 3 decompose to 1 kg Ca. O plus 1 kg CO 2? 3) for the reactions: CH 4+2 O 2=CO 2+2 H 2 O - Can we say 1 m 3 CH 4 reacts with 2 m 3 O 2 giving 1 m 3 CO 2 & 2 m 3 H 2 O? Why? - We need a quantitative conversion between the number of atoms/molecules and the everyday’s mass units (macroscopic). The conversion is done through the Mole, by definition I mole =6. 023 x 1023 molecules/atoms Avocados number or Avocados constant 4

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole and Molar Mass q For any substances, the number of atoms, molecules (including isotopes) and ions in ONE mole is a fixed number I mole =6. 023 x 1023 atoms/molecules/ions q Conversion of mass in a. m. u. scale to that in gram scale numerically: 1 a. m. u. x 6. 023 x 1023 = 1 gram q The mass of ONE mole of substance is called Molar Mass e. g. Mass of a carbon (C) atom=12. 0 a. m. u. number of C atoms in 1 mole=6. 023 x 1023 MOLAR MASS of C =12 x 1 gram/(a. m. u. x 6. 023 x 1023)=12 gram (per mole) Þ The molar mass has the same value as that of a. m. u for an atom/molecule, but it is in gram. Molar weight has the same value as that of molar mass on earth. 5

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole and Molar Mass I mole =6. 023 x 1023 molecules/atoms Molar Mass - The mass of one mole substance Element mass of one atom number of atoms in one mole The mass of one molar mass H 1. 008 a. m. u 6. 023 x 1023 1. 008 gram He 4. 009 a. m. u 6. 023 x 1023 4. 009 gram Li 6. 941 a. m. u 6. 023 x 1023 6. 941 gram molecule / ion mass of one molecule number of molecules /ions in one mole The mass of one molar mass CO 2 44 a. m. u. 6. 023 x 1023 44 gram H 2 O 18 a. m. u. 6. 023 x 1023 18 gram SO 4= 96 a. m. u. 6. 023 x 1023 96 gram 6

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole - Calculations Questions: 1). Calculate the number of molecules and the number of oxygen atoms in 0. 25 moles of calcium nitrate Ca(NO 3)2. 2). What is the molar mass of Ca(NO 3)2? What is the mass of 0. 25 mole of Ca(NO 3)2? 3). What is the number of moles of 82 gram of Ca(NO 3)2? How many nitrogen atoms in it? 1) Number of Ca(NO 3)2 molecules =0. 25 mol x 6. 022 x 1023 molecules/mol= 1. 5 x 1023 molecules Number of oxygen atoms = 0. 25 mol x 6. 022 x 1023 molecules/mol x 6 O atoms/molecule = 9. 0 x 1023 atoms 2) Molar mass =1 x 40(Ca)+2 x 14(N)+6 x 16(O)=164 gram/mole The mass of 0. 25 mole of Ca(NO 3)2 =0. 25 mol x 164 g/mole=41 gram 3) Number of moles =82 gram / 164 gram/mole=0. 5 moles Number of N atoms = 0. 5 mole x 6. 022 x 1023 molecules/mol x 2 N atoms/molecule = 6. 0 x 1023 atoms 7

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole - Calculations Questions: 1). Calculate the mass of 2 moles of H 2 SO 4 and the mass of of 2 moles of SO 4=. 2). Calculate the number of moles and the number of oxygen in 1 tea-spoon of sugar (2 g). 1) The mass of 2 moles of H 2 SO 4 = 2 mole x molar mass of H 2 SO 4 =2 x [2 x 1(H)+1 x 32(S)+4 x 16(O)]=2 x 98=196 gram The mass of 2 moles of SO 4= = 2 mole x molar mass of SO 4= =2 x [1 x 32(S)+4 x 16(O)]=2 x 96=192 gram 2) Number of moles of 2 gram C 12 H 22 O 11 molecules =2 g/ molar mass of C 12 H 22 O 11 =2/[12 x 12(C)+22 x 1(H)+11 x 16(O)]=2/342=0. 005848 mole Number of oxygen atoms = 0. 005848 mol x 6. 022 x 1023 molecules/mol x 11 O atoms/molecule=3. 874 x 1022 oxygen atoms 8

CH 4751 Lecture Notes 7 (Erzeng Xue) Matter - The Mole - Calculations Questions: 1). The gas fired central heating system at home involves combustion of methane with oxygen. The reaction occurs being: CH 4 + 2 O 2 = 2 H 2 O + CO 2 + Heat. It means that for every mole of methane burnt, two moles of oxygen are required and this gives, in addition to the heat, 2 moles of H 2 O and one mole of CO 2 as the result of the reaction. Calculate how many grams of CO 2 is generated by heating the house for 1 hour, assuming the rate of CH 4 consumption is 5 m 3 (STP) per hour and the density of gas is 1 kg/m 3. 1) 2) The mass of gas consumed in 1 hour = 1 kg/m 3 x 5 m 3/hour=5 kg/hour The number of moles of gas consumed in one hour =5 kg x 1000 g/kg / molar mass of CH 4=5000/[1 x 12(C)+4 x 1(H)]=312. 5 moles/hour 3) The number of moles of CO 2 generated 1 mole CO 2 per mole of CH 4 x moles of CH 4 consumed=1 x 312. 5=312. 5 moles CO 2/hour 4) The mass (weight) of CO 2 generated in one hour = 312. 5 mole x molar mass of CO 2 =312. 5 x [1 x 12(C)+2 x 16(O)]=312. 5 x 44=13750 gram 9

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Solution - The Molarity q When a solution (solute+solvent) is concerned, the concentration of solute is usually defined as the number of moles of solute in the total volume of solution. moles of solute Molarity = unit mol/L or referred as molar or M litres of solution e. g. If a sulphuric acid solution is marked as 4 M. It means that one litre of solution (water+sulphuric acid) contains 4 moles of H 2 SO 4. Note: Molarity refers to concentration. For a solution of the same molarity, the larger the volume is the more the number of moles of solute it contains. The volume used in calculating the molarity includes both solute and solvent. Question: 1) How many moles of H 2 SO 4 are there in 250 ml of 4 M H 2 SO 4 solution? 2) Are the molarities of the following solutions the same or different? 2 moles in 4 litres solution, 0. 4 moles in 800 ml solution 10

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Molarity Calculations Examples 1). What is the molarity of a solution made by dissolving 2. 355 g of sulphuric acid (H 2 SO 4) in water and diluting to a final volume of 50 ml? Molar mass of H 2 SO 4 = 2 x 1. 0(H)+1 x 32. 1(S)+4 x 16. 0(O)=98. 1 gram/mol number of moles in 2. 335 g H 2 SO 4 =2. 335(g) x 1/98. 1(g/mol)=0. 024 mol of H 2 SO 4 Molarity = moles of solute/ Litres of solution=0. 024 mol / 0. 05 L=0. 48 M. 2). If the above solution is added to another 50 ml water, what is the concentration of the resultant solution? Will the molarity of solution remain the same? Will the number of moles of H 2 SO 4 in the solution remains the same? 3). If the we take 10 ml of the solution in 1) and add it into another 100 ml of water, what is the concentration of resultant solution? molarity=[(0. 024 mol/50 ml)x 10 ml]/(10 ml+100 ml)=0. 0436 M (or mol/L) 11

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas q When a gas is concerned, the concentration of a gas, A, in a gas mixture, A+B, (usually in a confined space) can be expressed by means of mole fraction moles of A Mole fraction of A = total moles of A+B or moles of A mole percentage of A = total moles of A+B unit mol/mol or -/- x 100% Note: Unlike a solution, the volume of a gas is very sensitive to the temperature and pressure. Therefore, when quoting the volume of a gas, T & P must be given. e. g. Air contains 78% of nitrogen (N 2) and 21% of oxygen (O 2 ), which means that in every 100 moles of air there are 78 moles of N 2 and 21 moles of O 2 (There also trace amount of Ar, CO 2 and other gases). N 2 mole fraction=78/100=0. 78 N 2 mole % =(78/100)x 100%=78% O 2 mole fraction=21/100=0. 21 O 2 mole % =(21/100)x 100%=21% 12

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas q The pressure and concentration of a gas m m q Pressure by definition is the force exerted collectively by gas molecules colliding on the surface (in all walls of a container) of unit area. Within a same space (volume) at the same temperature, the more gas molecules there are, the more intense the collision of these molecules on the wall, thus a higher pressure it will be. For most common gases, the following relation is observed Where P - absolute pressure; V - volume of gas; n - number of mole of gas; R - gas constant; T - absolute temperature (Kelvin scale) (Note that the term n/V has meaning of ‘volume concentration’) The equation is called Ideal Gas Law (or Perfect Gas Law) m A gas which obeys this relation is called ideal gas (or perfect gas) m It is usually more convenient to measure the pressure of a gas. m 13

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas q Concept of partial pressure m If a gas mixture contains n 1 moles of A, n 2 moles of B, n 3 moles of C, …, the mixture is held in a container of vol. V and kept at temperature T, for each gas, we can write: where Ptotal=P 1+P 2+P 3+… ntotal=n 1+n 2+n 3+… mole ratio mole fraction pressure ratio pressure fraction volume ratio volume fraction m Pi is called partial pressure of a component i, which can be regarded as ‘a fraction of pressure’ contributed by each component to the overall pressure. m The pressure/volume ratio of gases in a mixture is directly proportional to their mole ratio m The pressure/volume fraction of a gas in a mixture is proportional to its mole fraction 14

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas q Some important concepts about gas m m For ideal gas its volume, V, is proportional to the number of moles of matter, n, and is independent of the type of substance - which means that ONE mole of any gases will have the same volume (molar volume) at the same pressure & temperature. m q Most common gases show behaviour close to ideal gas, especially at low pressure and high temperature (when gas molecules are far apart) From ideal gas law, any 3 of 4 variables (P-V-n-T) will determine the 4 th variable. Some usage of partial pressure concept m Quantifying each of gas components in a gas mixture m Characterising systems that contain multi-phase such as gas-liquid, gas solid etc. m Analysing systems that involve phase change m Describing reactions that have reactants and/or products present in both g&l phases m Relating certain solution properties with gas phase pressure (e. g. solubility) m etc. 15

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas Examples 1). Air contains 78% of N 2 and 21% of O 2 Þ these can be considered as mole fractions as well as volume fractions (Note: When quoting a percentage of a gas in a mixture, it is better to label the percentage sign with a proper abbreviation, e. g. : vol. % or wt. % to avoid confusion) if air pressure is 1 atm. , the N 2 partial pressure PN 2=0. 78 atm the O 2 partial pressure PO 2=0. 21 atm 2). A gas cylinder at 200 bar contains 5% hydrogen (H 2) in Argon (Ar). What is the mole fraction of each gas? What is the partial pressure of each gas? Þ When we say 5% H 2 in Ar, usually we mean the vol. %; as for gas the vol. % has the same value as that of mol%, we don’t normally put ‘vol. ’ before the % sign. The % here however, is definitely not wt. % (wt. % is rarely used to describe a gas mixture). mole fraction for H 2: 5%=0. 05, partial pressure: since for H 2 and for Ar: 0. 05 x 200=10 bar, for Ar: (100%-5%)95%=0. 95 x 200=190 bar 16

CH 4751 Lecture Notes 8 (Erzeng Xue) Matter - Quantities Concentration of a Gas Examples 1). Calculate from the ideal gas law the volume of 1 mole gas at 0°C and 20°C and 1 atm. at 0°C at 20°C 2). Reaction 2 NO + O 2 = 2 NO 2 occurs at 2 bar and 300°C. Initially there are 200 moles of NO and 200 moles of O 2. After time t, 120 moles of NO is converted. Calculate the partial pressure of each component in the gas phase at t, assuming the pressure remains constant. Ans. initial moles change at t 2 NO 200 -120 200 -60 + 0 +120 O 2 = 2 NO 2 total moles at t gas mixture at t 200 -120=80 200 -60=140 120 mole fraction(ni /ntotal) 80/340=0. 235 140/340=0. 411 pressure fraction (Pi /Ptotal)0. 235 0. 412 0. 353 since Ptotal=2 bar the partial pressure at t, PNO=0. 470 PO 2=0. 824 ntotal=80+140+120=340 120/340=0. 353 PNO 2=0. 706 bar 17

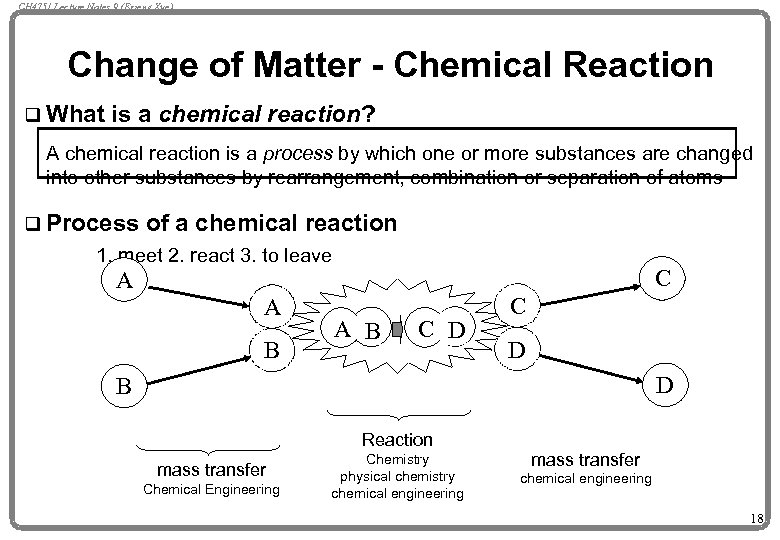CH 4751 Lecture Notes 9 (Erzeng Xue) Change of Matter - Chemical Reaction q What is a chemical reaction? A chemical reaction is a process by which one or more substances are changed into other substances by rearrangement, combination or separation of atoms q Process of a chemical reaction 1. meet 2. react 3. to leave C A A B C D D B Reaction mass transfer Chemical Engineering Chemistry physical chemistry chemical engineering mass transfer chemical engineering 18

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Topics To Study q What we are going to study in this module m Quantitative representation of a chemical reaction Ø m Factors deciding if a chemical reaction can proceed in the direction specified Ø m Reaction thermodynamics If a chemical reaction can proceed, what conversion level can be achieved? Ø m Reaction stoichiometry / reaction equation Chemical equilibrium If a chemical reaction can proceed, how fast it will go? Reaction kinetics Ø Catalysis Ø m q Types of chemical reaction commonly encountered What are the objectives we want to achieve after study m When you encounter a chemical reaction You should be able to make judgement if a reaction is feasible Ø If reaction is feasible, you should be able predict the level of conversion Ø You should be able to understand some basic concepts of reaction kinetics Ø 19

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Reaction Equation q Chemical reaction equation (D H T ) v. AA + v. BB = v. CC + v. DD Ø It shows the substances participating in reaction (reactants) and the substances that are formed as the consequence of the reaction (products). Ø It shows the ‘direction’ of reaction (reactants on the left & products on the right). Ø It shows the ratio of number of molecules or moles of reactants as well as products, the ratios are given by v. A, v. B, v. C & v. D which are reaction stoichiometry coefficients. stoichiometry coefficient v. A v. B v. C v. D e. g. CH 4 + 2 O 2 = CO 2 + 2 H 2 O Ca. CO 3 = Ca. O + CO 2 C 6 H 12 O 6 + 6 O 2 = 6 CO 2+ 6 H 2 O Ø Sometime 1 2 1 - 1 1 1 6 6 6 additional information, e. g. the amount reaction heat involved is indicated. 20

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Reaction Equation q More on reaction equation Sometime a chemical equation may appear in different forms: v. AA + v. BB = v. CC + v. DD v. AA + v. BB ® v. CC + v. DD v. AA + v. BB v. CC + v. DD m The sign between reactants and products Ø If an equal sign ‘=’ is used, it indicates the exact number of reactant molecules required to react each other and the number of product molecules to form e. g 2 NO+O 2=2 NO 2 (2 moles of NO react with 1 mole of O 2 forming 2 moles of NO 2) Ø If an arrow sign ‘®’ is used, it usually indicates the substances to react and the substances formed without emphasising the no. of molecules of each substances e. g NO+O 2=NO 2 (NO will react with O 2 giving NO 2) Ø If a sign ‘ ’ is used, it usually indicates that the reactants cannot convert completely to products because the presence of reverse reaction (equilibrium controlled) e. g 2 NO+O 2 2 NO 2 (Reaction of NO with O 2 forming NO 2 is equilibrium controlled) 21

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Reaction Stoichiometry q More on reaction equation m v. AA + v. BB = v. CC + v. DD The reaction stoichiometry coefficients, v. A, v. B, v. C & v. D Ø These numbers are usually integral, Sometime fraction numbers are seen in literature. Generally integral number is preferred. Ø When the value of a coefficient is ‘ 1’, it is commonly omitted. Ø The coefficients are determined in such way that the sum of each atom in all reactants should be equal to the sum of the same atom in all products. m The process to determine these coefficients is called balancing reaction equation General methods of balancing reaction equation Ø Simple Ø When Ø From reaction equation - by inspection no. of coefficients - 1 £ no. of atom types Þ solve coefficient equations oxidation state changes. 22

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Balancing Reaction Equation q Balancing equation by inspection m Start with most complex formula Þ balance by changing adjustable coefficients Þ leave H and O until last Þ check your answer by the sum of no. atoms on each side e. g. Al + HCl ® Al. Cl 3 + H 2 Al. Cl 3 most complex Þ 3 Cl on r. h. s. , 1 Cl on l. h. s. Þ set 3 for HCl Þ Al + 3 HCl ® Al. Cl 3 + H 2 3 H on l. h. s. , 2 H on r. h. s. Þ set 6 for HCl and 3 for H 2 and 2 for Al. Cl 3 Þ Al + 6 HCl ® 2 Al. Cl 3 + 3 H 2, 1 Al on l. h. s. , 2 Al on r. h. s. Þ set 2 for Al, Þ we now have: 2 Al + 6 HCl = 2 Al. Cl 3 + 3 H 2 Check: Al: 2 on l. h. s. º 2 on r. h. s. ; Cl: 6 on l. h. s. º 6 on r. h. s. ; 23 H: 6 on l. h. s. º 6 on r. h. s. 6. Þ Balancing completed.

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Balancing Reaction Equation q Balancing equation by solving coefficient equations adjustable coefficients a C 2 H 4 + b O 2 ® m CO 2 + n H 2 O e. g. l. h. s: [C]L = 2 a, [H]L = 4 a, [O]L = 2 b r. h. s: [C]R= m, [H]R = 2 n, [O]R = 2 m+n For [C]L = [C]R Þ 2 a = m not adjustable coefficient equations [H]L = [H]R Þ 4 a = 2 n [O]L = [O]R Þ 2 b = 2 m+n There are 4 coefficients and 3 equations. Let a =1, the rest coefficients can be solved. We have m = 2, n =2, b = 3 C 2 H 4 + 3 O 2 = 2 CO 2 + 2 H 2 O Balancing completed. 24

CH 4751 Lecture Notes 9 (Erzeng Xue) Chemical Reactions Balancing Reaction Equation q Balancing equation by oxidation state changes a Mn. O 4 - + b C 2 O 42 - + c H+ ® d Mn 2+ + e H 2 O + f CO 2 +7 +3 +4 +2 Coefficient equation method fails to produce the coefficient. reduction oxidation r. h. s. coeff. eqns Mn a d a=d Gain 5 e- / from Mn. O 4 to Mn 2+ m I. h. s. O 4 a+4 b e+2 f 4 a+4 b=e+2 f Lost e- by C 2 O 42 - = gain e- by Mn. O 4 - C 2 b f 2 b=f H c 2 e c=2 e Lose 1 e- / C or 2 e- / C 2 O 4 2 - - m 2 - - Þ ratio C 2 O 4 : Mn. O 4 is 5 : 2 Þ 2 Mn. O 4 - + 5 C 2 O 42 - + H+ ® Mn 2+ + H 2 O + CO 2 m By inspection 2 Mn. O 4 - + 5 C 2 O 42 - + 16 H+ = 2 Mn 2+ + 8 H 2 O + 10 CO 2 Check: l. h. s. : 2 Mn, 28 O, 10 C and 16 H; [l. h. s. ] º [r. h. s. ] r. h. s. 2 Mn, 28 O, 10 C and 16 H balancing is complete 25

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Types of Chemical Reactions q Based on the ways substances change in a chemical reaction, we can classify chemical reactions into 5 basic types m Combination reactions m Decomposition reactions m Double displacement or exchange reactions m Neutralisation reactions m Oxidation - Reduction - (redox) reactions 26

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Combination Reactions q Two or more substances react and forms one product Combination reaction e. g. A + B ® C 2 H 2 + O 2 ® 2 H 2 O Ca. O + H 2 O ® Ca(OH)2 m Many elements react with each other in combination reactions to form compounds e. g. m N 2 + 3 H 2 ® 2 NH 3 A combination reaction betw. a metal & a nonmetal produces an ionic compound e. g. 2 Mg + O 2 ® 2 Mg. O 27

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Decomposition Reactions q One substance undergoes a reaction producing more than 1 products Decomposition reaction A ® B + C e. g. 2 H 2 O ® 2 H 2 + O 2 2 Na. N 3 ® 2 Na + 3 N 2 Ø m A decomposition reaction used to inflate the air bag in cars. On impact reaction is ignited and produce quickly a large volume gas (10 g Na. N 3 gives 50 litres N 2) Many compounds undergo decomposition when heated e. g. Ø Ca. CO 3 ® Ca. O + CO 2 A commercial process to produce lime from limestone decomposition. 28

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Double Displacement or Exchange Reactions q Exchange ionic partners between two ionic compounds Double displacement reaction A X + B Y ® A Y + B X where A, B are cations (positive ions) X, Y are anions (negative ions) e. g. 2 Na. OH (aq) + Mg(NO 3)2(aq) ® Mg(OH)2(s) + 2 Na. NO 3 (aq) KCl (aq) + Ag. NO 3(aq) ® Ag. Cl(s) + KNO 3(aq) Ø Precipitates are often formed in this type of reaction. 29

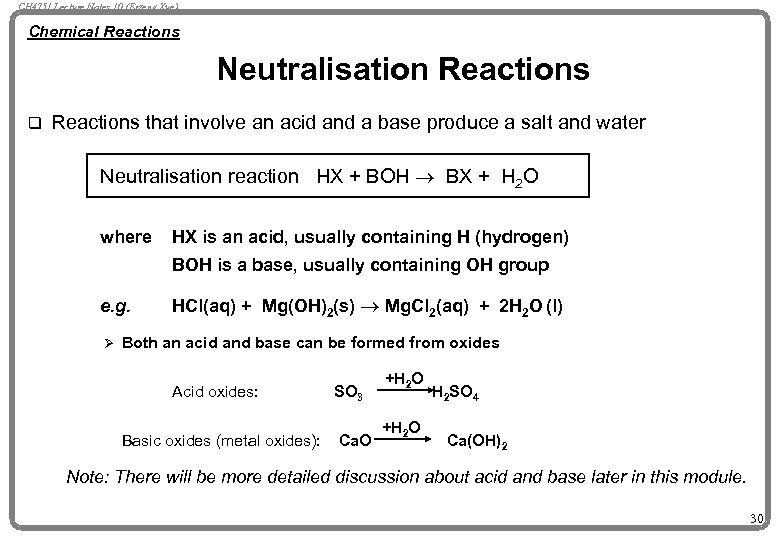CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Neutralisation Reactions q Reactions that involve an acid and a base produce a salt and water Neutralisation reaction HX + BOH ® BX + H 2 O where HX is an acid, usually containing H (hydrogen) BOH is a base, usually containing OH group e. g. Ø HCl(aq) + Mg(OH)2(s) ® Mg. Cl 2(aq) + 2 H 2 O (l) Both an acid and base can be formed from oxides Acid oxides: Basic oxides (metal oxides): SO 3 Ca. O +H 2 O H 2 SO 4 Ca(OH)2 Note: There will be more detailed discussion about acid and base later in this module. 30

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions Oxidation-Reduction Reactions q Reactions that involve oxidation of one reactant and reduction of another gains e-’s Oxidation-Reduction reaction A + BZ ® AZ + B loses e-’s Oxidation - a chemical process by which an entity loses electrons. Reduction - a chemical process by which an entity gains electrons. (Remember as: OIL RIG - Oxidation Is Loss, Reduction Is Gain) e. g. is reduced 2 Mg 0 + O 20 ® 2 Mg 2+O 2 - (2 Mg. O) H 20 + F 20 ® 2 H+F- (2 HF) Mg (loses 2 e-’s) is oxidised, O (gains 2 e-’s) H (loses 1 e-) is oxidised, F (gains 1 e-) is reduced Ø Each electron that is gained by one species must be lost by another, which means the oxidation and reduction always occurs in pair. Ø This type reaction is often referred as Redox reaction (Reduction Oxidation) (Note: The Redox reaction does not necessitate the participation of oxygen. ) 31

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions More about Redox Reactions BZ gains e-’s - being reduced ® called oxidant (oxidising A) Redox reaction A + BZ ® AZ + B A loses e-’s - being oxidised ® called reductant (reducing BZ) m In the rxn reactant A is oxidised by reactant BZ; in the meantime BZ is reduced by A. Ø Ø m The reactant that oxidises another is called oxidant (e. g. BZ in the above reaction), the oxidant itself is reduced as the result of oxidising the other reactant (A). The reactant that reduces another is called reductant (e. g. A in the above rxn), the reductant itself is oxidised as the result of reducing the other reactant (BZ). A species carries electronic charge if gained or lost electrons. The sign and magnitude of the charge is called Oxidation State or Oxidation Number. e. g. In Mg. O the O. S. of Mg is 2+ & O is 2 - H 20 + F 20 ® 2 H+F- (2 HF) Ø 2 Mg 0 + O 20 ® 2 Mg 2+O 2 - (2 Mg. O) In HF the O. S. of H is 1+ & F is 1 - Oxidation state of some elements in compounds: - Usually H: 1+, O: 2 -, halogens (F, Cl, Br, I) 1 -. - Metal ions: 1 A group 1+, 2 A group 2+, transition groups variable, but all metal ions are invariably positive. - Some elements have variable o. s. , depending on the compounds they are in, e. g. Cu+, Cu 2+, S+2, S+6, S+7. 32

CH 4751 Lecture Notes 10 (Erzeng Xue) Chemical Reactions q Examples Classify the following reactions HNO 3 (aq) + Na. OH (aq) ® Na. NO 3 (aq) + H 2 O Cu(OH)2(s) ® Cu. O(s) Neutralisation + H 2 O(l) Decomposition Ba. Cl 2(aq) + K 2 SO 4(aq) ® Ba. SO 4(s) + 2 KCl(aq) 2 Ca(s) + O 2(g) ® 2 Ca. O(s) Exchange Redox / combination Cl 2(g) + 2 Na. Br(aq) ® 2 Na. Cl(aq) + Br 2(aq) Redox q Calculate the oxidation state of S in 1) SCl 2, 2) SO 42 -, 3) S 2 O 82 - & Mn in KMn. O 4 1). In a molecule, the sum of O. S. (charges) of all atoms in the molecule is zero (O. S. [S]) + 2 x(O. S. [Cl])=(0) Þ (O. S. [S]) + 2 x(1 -)=(0) Þ (O. S. [S])=(2+) 2). In an ion, the sum of O. S. of all atoms in the ions equal to overall charge (O. S. [S]) + 4 x(O. S. [O])=(2 -) Þ (O. S. [S]) + 4 x(2 -)=(2 -) Þ (O. S. [S])=(6+) 3) 2 x(O. S. [S]) + 8 x(O. S. [O])=(2 -) Þ 2 x(O. S. [S]) + 8 x(2 -)=(2 -) Þ (O. S. [S])=(7+) 4) (O. S. [K])+(O. S. [Mn])+4 x(O. S. [O])=(0) Þ (1+)+(O. S. [Mn])+4 x(2 -)=(0) Þ (O. S. [Mn])=(7+) 33