Ch 4 — Electrons in Atoms I Waves

Ch. 4 - Electrons in Atoms I. Waves & Particles

Light and Electrons z. Because light and electrons have common properties, understanding one helps to understand the other.

Electromagnetic radiation z. Energy that exhibits wave-like behavior as it travels z. Includes: gamma rays, X-rays, infrared, visible spectrum, microwaves, ultraviolet rays, radio and TV waves

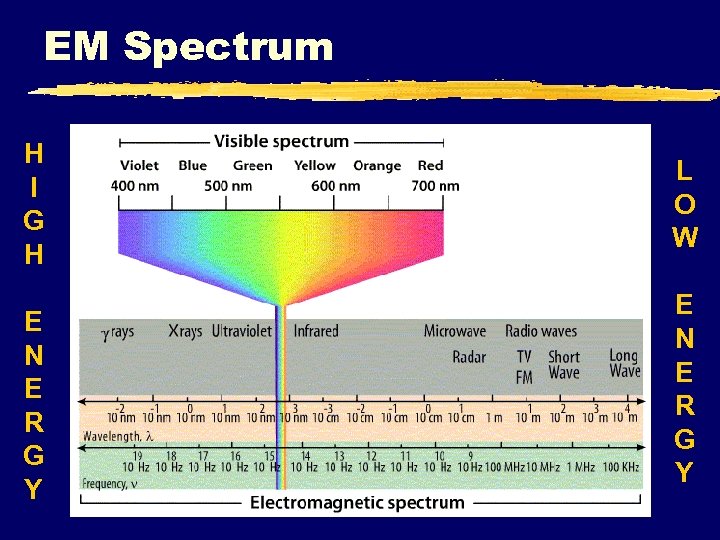EM Spectrum H I G H E N E R G Y L O W E N E R G Y

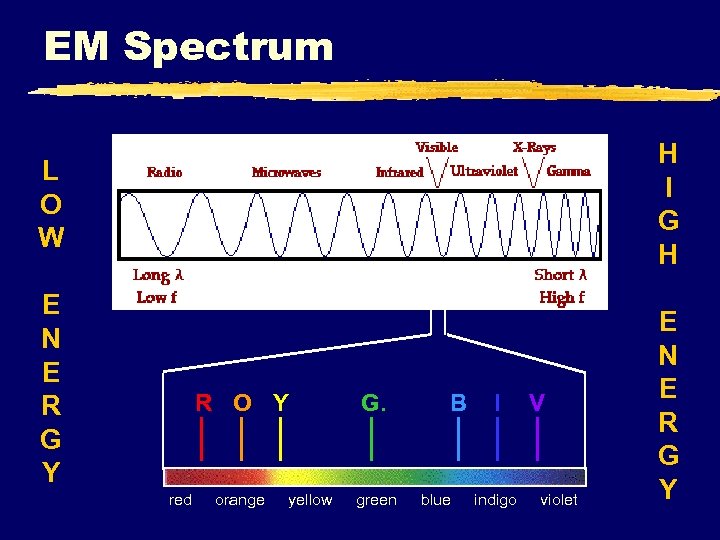EM Spectrum H I G H L O W E N E R G Y R O Y red G. orange green yellow B blue I indigo V violet E N E R G Y

Waves z. Wavelength ( ) - length of one complete wave (measured in m, cm, nm) z. Frequency ( ) - # of waves that pass a point during a certain time period yhertz (Hz) = 1/s (s-1) z. Amplitude (A) - distance from the origin to the trough or crest

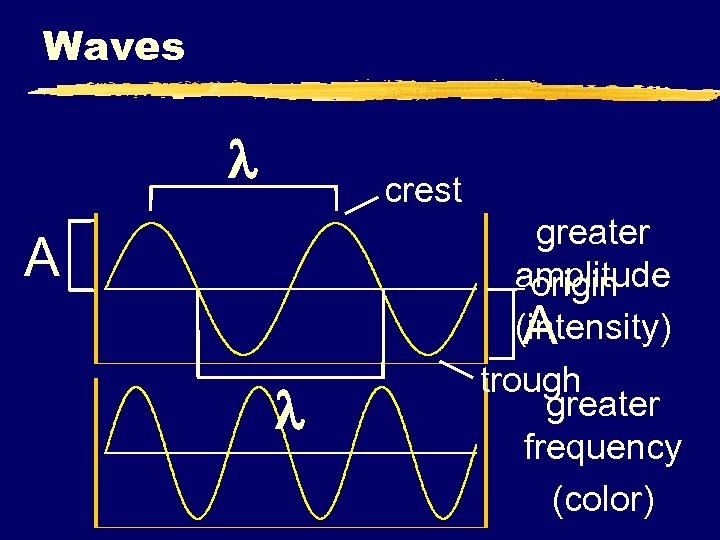Waves crest A greater amplitude origin (intensity) A trough greater frequency (color)

EM Spectrum z. Frequency & wavelength are inversely proportional c = c: speed of light (3. 00 108 m/s) : wavelength (m, nm, etc. ) : frequency (Hz)

EM Spectrum z. EX: Calculate the wavelength of radiation whose frequency is 7. 50 x !012 Hz. GIVEN: WORK: = 7. 50 x !012 =c = 3. 00 108 m/s Hz =? c = 3. 00 108 m/s 7. 50 1012 Hz = 4. 00 10 -5 m

Light as Particles z. A property which could not be explained in terms of waves was a phenomenon known as the photoelectric effect – refers to the emission of electrons from a metal when heated or lit.

Quantum Theory z. Planck (1900) y. Observed - emission of light from hot objects y. Concluded - energy is emitted in small, specific amounts (quanta) y. Quantum - minimum amount of energy change

Quantum Theory z. Planck (1900) vs. Classical Theory Quantum Theory

Quantum Theory z. The energy of a photon is proportional to its frequency. E = h E: energy (J, joules) h: Planck’s constant (6. 6262 10 -34 J·s) : frequency (Hz)

Quantum Theory z. EX: Find the energy of a photon with a frequency of 3. 55 1017 Hz. GIVEN: WORK: E=? E = h = 3. 55 1017 Hz E = (6. 6262 10 -34 J·s) h = 6. 6262 10 -34 (3. 55 1017 J·s Hz) -16

Quantum Theory z. Einstein (1905) y. Observed - photoelectric effect

Quantum Theory z. Einstein (1905) y. Concluded - light has properties of both waves and particles “wave-particle duality” y. Photon - particle of light, having zero mass, carrying a quantum of energy

Quantum Theory z. Radiation is emitted and absorbed only in whole numbers of photons

Ch. 4 - Electrons in Atoms II. Bohr Model of the Atom

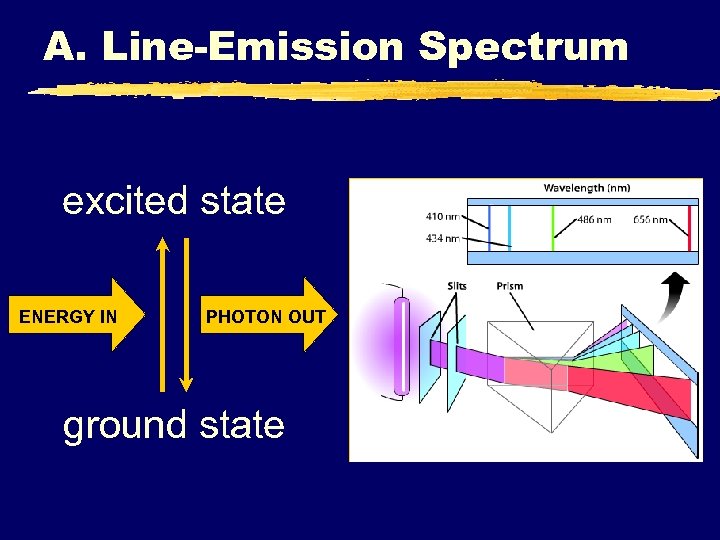A. Line-Emission Spectrum excited state ENERGY IN PHOTON OUT ground state

B. Bohr Model z. Linked the atom’s electron with photon emission ze- exist only in paths, or orbits, with specific amounts of energy called energy levels z. Therefore… ye- can only gain or lose certain amounts of energy yonly certain photons are produced

B. Bohr Model 65 4 3 2 1 z. Energy of photon depends on the difference in energy levels ze- jumps up when energy is absorbedgives off light when is falls back down

C. Other Elements z. Each element has a unique bright-line emission spectrum. y“Atomic Fingerprint” Helium z. Bohr’s calculations only worked for hydrogen!

z. Bohr’s model of the atom explained electrons as particles.

A. Electrons as Waves z. Louis de Broglie (1924) y. Applied wave-particle theory to e ye exhibit wave properties

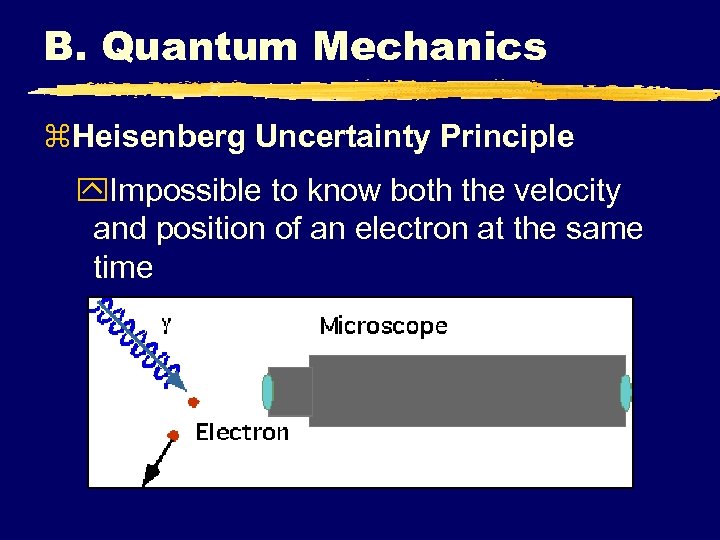B. Quantum Mechanics z. Heisenberg Uncertainty Principle y. Impossible to know both the velocity and position of an electron at the same time

B. Quantum Mechanics z. Schrödinger Wave Equation (1926) ytreated e- moving around the nucleus as waves ydefines probability of finding an eydefines mathematically the wave properties of electrons

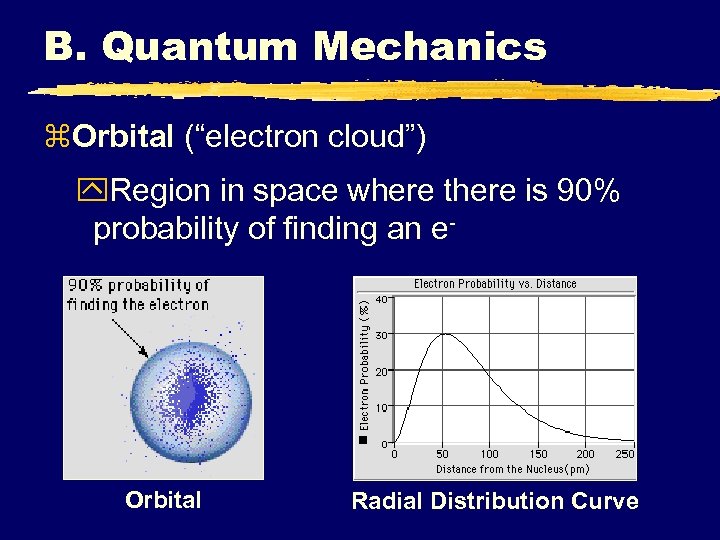B. Quantum Mechanics z. Orbital (“electron cloud”) y. Region in space where there is 90% probability of finding an e- Orbital Radial Distribution Curve