159643999a1fdf3b5d383202fca22bcb.ppt
- Количество слайдов: 38
 Ch. 2 - Time Value of Money 1
Ch. 2 - Time Value of Money 1
 Time Value of Money (applications) n Implied Interest Rates n Internal Rate of Return n Time necessary to accumulate funds 2
Time Value of Money (applications) n Implied Interest Rates n Internal Rate of Return n Time necessary to accumulate funds 2
 Example : Finding Rate of Return or Interest Rate n A broker offers you an investment (a zero coupon bond) that pays you $1, 000 five years from now for the cost of $740 today. n What is your annual rate of return? 3
Example : Finding Rate of Return or Interest Rate n A broker offers you an investment (a zero coupon bond) that pays you $1, 000 five years from now for the cost of $740 today. n What is your annual rate of return? 3
 4
4
 The Time Value of Money Compounding and Discounting Cash Flow Streams 0 1 2 3 4 5
The Time Value of Money Compounding and Discounting Cash Flow Streams 0 1 2 3 4 5
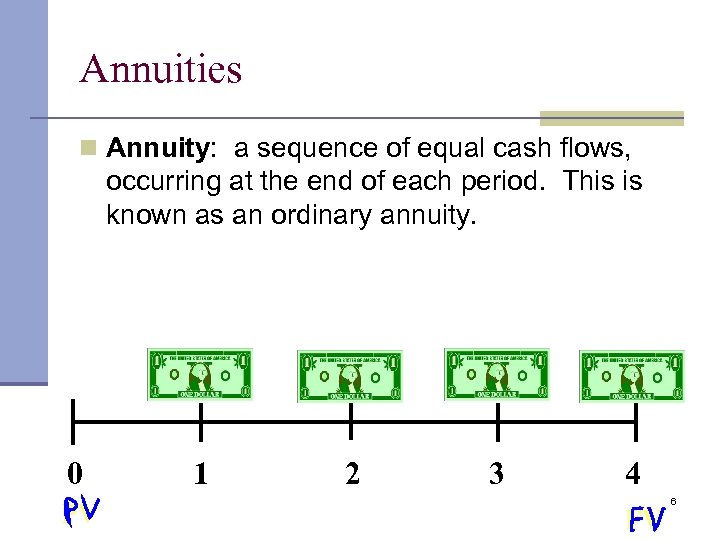 Annuities n Annuity: a sequence of equal cash flows, occurring at the end of each period. This is known as an ordinary annuity. 0 PV 1 2 3 4 FV 6
Annuities n Annuity: a sequence of equal cash flows, occurring at the end of each period. This is known as an ordinary annuity. 0 PV 1 2 3 4 FV 6
 Examples of Ordinary Annuities: n If you buy a bond, you will receive equal semi- annual coupon interest payments over the life of the bond. n If you borrow money to buy a house or a car, you will re-pay the loan with a stream of equal payments. 7
Examples of Ordinary Annuities: n If you buy a bond, you will receive equal semi- annual coupon interest payments over the life of the bond. n If you borrow money to buy a house or a car, you will re-pay the loan with a stream of equal payments. 7
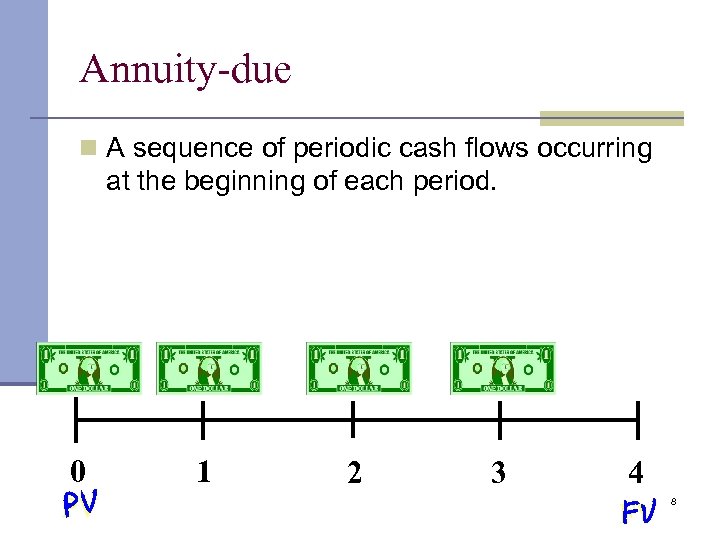 Annuity-due n A sequence of periodic cash flows occurring at the beginning of each period. 0 PV 1 2 3 4 FV 8
Annuity-due n A sequence of periodic cash flows occurring at the beginning of each period. 0 PV 1 2 3 4 FV 8
 Examples of Annuities-due n Monthly Rent payments: due at the beginning of each month. n Car lease payments. n Cable & Satellite TV and most internet service bills. 9
Examples of Annuities-due n Monthly Rent payments: due at the beginning of each month. n Car lease payments. n Cable & Satellite TV and most internet service bills. 9
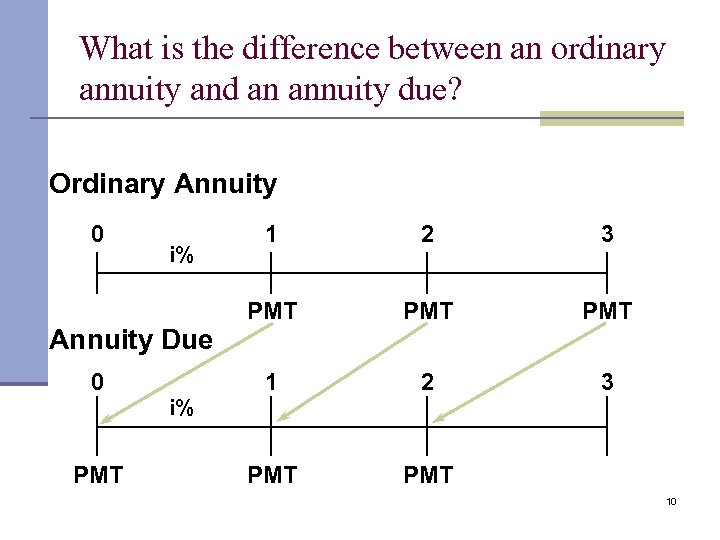 What is the difference between an ordinary annuity and an annuity due? Ordinary Annuity 0 i% Annuity Due 0 PMT i% 1 2 3 PMT PMT 1 2 3 PMT 10
What is the difference between an ordinary annuity and an annuity due? Ordinary Annuity 0 i% Annuity Due 0 PMT i% 1 2 3 PMT PMT 1 2 3 PMT 10
 Solving for FV: 3 -year ordinary annuity of $100 at 10% n $100 payments occur at the end of each period, but there is no PV. OUTPUT 3 10 0 -100 N INPUTS I/YR PV PMT FV 331 11
Solving for FV: 3 -year ordinary annuity of $100 at 10% n $100 payments occur at the end of each period, but there is no PV. OUTPUT 3 10 0 -100 N INPUTS I/YR PV PMT FV 331 11
 Solving for PV: 3 -year ordinary annuity of $100 at 10% n $100 payments still occur at the end of each period, but now there is no FV. OUTPUT 3 10 N INPUTS I/YR 100 PV 0 PMT FV -248. 69 12
Solving for PV: 3 -year ordinary annuity of $100 at 10% n $100 payments still occur at the end of each period, but now there is no FV. OUTPUT 3 10 N INPUTS I/YR 100 PV 0 PMT FV -248. 69 12
 Solving for FV: 3 -year annuity due of $100 at 10% n Now, $100 payments occur at the beginning of each period. n FVAdue= FVAord(1+I) = $331(1. 10) = $364. 10. n Alternatively, set calculator to “BEGIN” mode and solve for the FV of the annuity: BEGIN OUTPUT 3 10 0 -100 N INPUTS I/YR PV PMT FV 364. 10 13
Solving for FV: 3 -year annuity due of $100 at 10% n Now, $100 payments occur at the beginning of each period. n FVAdue= FVAord(1+I) = $331(1. 10) = $364. 10. n Alternatively, set calculator to “BEGIN” mode and solve for the FV of the annuity: BEGIN OUTPUT 3 10 0 -100 N INPUTS I/YR PV PMT FV 364. 10 13
 Solving for PV: 3 -year annuity due of $100 at 10% n Again, $100 payments occur at the beginning of each period. n PVAdue= PVAord(1+I) = $248. 69(1. 10) = $273. 55. n Alternatively, set calculator to “BEGIN” mode and solve for the PV of the annuity: BEGIN OUTPUT 3 10 N INPUTS I/YR 100 PV 0 PMT FV -273. 55 14
Solving for PV: 3 -year annuity due of $100 at 10% n Again, $100 payments occur at the beginning of each period. n PVAdue= PVAord(1+I) = $248. 69(1. 10) = $273. 55. n Alternatively, set calculator to “BEGIN” mode and solve for the PV of the annuity: BEGIN OUTPUT 3 10 N INPUTS I/YR 100 PV 0 PMT FV -273. 55 14
 Annuities Applications n Value of payments n Implied interest rate for an annuity n Calculation of periodic payments Mortgage payment n Annual income from an investment payout n Future Value of annual payments n 15
Annuities Applications n Value of payments n Implied interest rate for an annuity n Calculation of periodic payments Mortgage payment n Annual income from an investment payout n Future Value of annual payments n 15
 Example: Invest Early in an IRA n How much would you have at age 65 if you deposit $2, 400 at the end of each year in an investment account with a 9% expected annual return starting at: (A) age 44? n (B) age 22? n 16
Example: Invest Early in an IRA n How much would you have at age 65 if you deposit $2, 400 at the end of each year in an investment account with a 9% expected annual return starting at: (A) age 44? n (B) age 22? n 16
 A) Start at age 44 17
A) Start at age 44 17
 B) Start at age 22 18
B) Start at age 22 18
 Solving for PMT: How much must the 44 -year old deposit annually to catch the 22 -year old? n To find the required annual contribution, enter the number of years until retirement and the final goal of $1, 058, 030 and solve for PMT. OUTPUT 21 9 0 N INPUTS I/YR PV 1, 058, 030 PMT FV -18, 639 19
Solving for PMT: How much must the 44 -year old deposit annually to catch the 22 -year old? n To find the required annual contribution, enter the number of years until retirement and the final goal of $1, 058, 030 and solve for PMT. OUTPUT 21 9 0 N INPUTS I/YR PV 1, 058, 030 PMT FV -18, 639 19
 Now about this? n Let’s assume that the 44 -year old has already accumulated $120, 000 in the IRA account. How much would he have to deposit on an annual basis at the 9% expected annual return to catch up with the 22 -year old and be a millionaire at age 65? 20
Now about this? n Let’s assume that the 44 -year old has already accumulated $120, 000 in the IRA account. How much would he have to deposit on an annual basis at the 9% expected annual return to catch up with the 22 -year old and be a millionaire at age 65? 20
 21
21
 More Annuity Fun! n Springfield mogul Montgomery Burns, age 85, wants to retire at age 100 so he can steal candy from babies full time. Once Mr. Burns retires, he wants to withdraw $100 million at the beginning of each year for 10 years from a special off-shore account that will pay 20% annually. In order to fund his retirement, Mr. Burns will make 15 equal end-of-the-year deposits in this same special account that will pay 20% annually. How large of an annual deposit must be made to fund Mr. Burns’ retirement plans? 22
More Annuity Fun! n Springfield mogul Montgomery Burns, age 85, wants to retire at age 100 so he can steal candy from babies full time. Once Mr. Burns retires, he wants to withdraw $100 million at the beginning of each year for 10 years from a special off-shore account that will pay 20% annually. In order to fund his retirement, Mr. Burns will make 15 equal end-of-the-year deposits in this same special account that will pay 20% annually. How large of an annual deposit must be made to fund Mr. Burns’ retirement plans? 22
 23
23
 Perpetuities n Suppose you will receive a fixed payment every period (month, year, etc. ) forever. This is an example of a perpetuity. n PV of Perpetuity Formula PMT = periodic cash payment i = interest rate 24
Perpetuities n Suppose you will receive a fixed payment every period (month, year, etc. ) forever. This is an example of a perpetuity. n PV of Perpetuity Formula PMT = periodic cash payment i = interest rate 24
 Perpetuities & Annuities Example - Perpetuity You want to create an endowment to fund a football scholarship, which pays $15, 000 per year, forever, how much money must be set aside today if the rate of interest is 5%? 25
Perpetuities & Annuities Example - Perpetuity You want to create an endowment to fund a football scholarship, which pays $15, 000 per year, forever, how much money must be set aside today if the rate of interest is 5%? 25
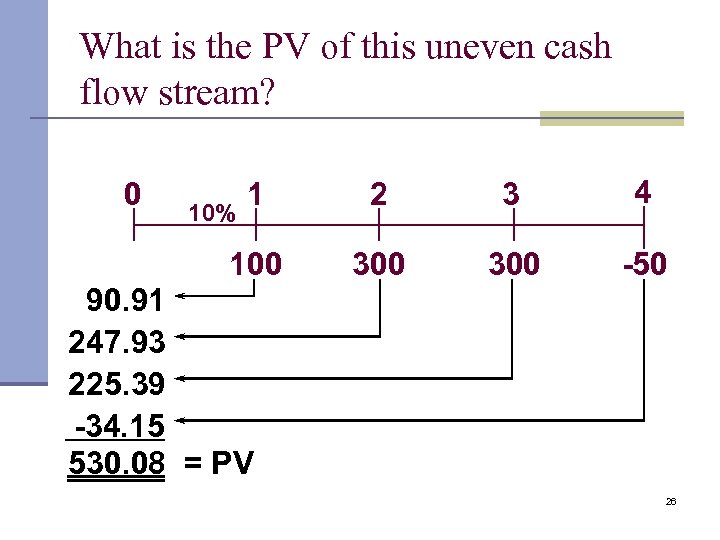 What is the PV of this uneven cash flow stream? 1 2 3 4 100 0 300 -50 10% 90. 91 247. 93 225. 39 -34. 15 530. 08 = PV 26
What is the PV of this uneven cash flow stream? 1 2 3 4 100 0 300 -50 10% 90. 91 247. 93 225. 39 -34. 15 530. 08 = PV 26
 Solving for PV: Uneven cash flow stream n Input cash flows in the calculator’s “CF” register: CF 0 = 0 n CF 1 = 100 n CF 2 = 300 n CF 3 = 300 n CF 4 = -50 n n Under NPV, enter I = 10, down arrow, and press CPT button to get NPV = $530. 087. (Here NPV = PV. ) 27
Solving for PV: Uneven cash flow stream n Input cash flows in the calculator’s “CF” register: CF 0 = 0 n CF 1 = 100 n CF 2 = 300 n CF 3 = 300 n CF 4 = -50 n n Under NPV, enter I = 10, down arrow, and press CPT button to get NPV = $530. 087. (Here NPV = PV. ) 27
 The Time Value of Money Non-annual Interest Compounding and Discounting 28
The Time Value of Money Non-annual Interest Compounding and Discounting 28
 Classifications of interest rates n Nominal rate (INOM) – also called the quoted or state rate. An annual rate that ignores compounding effects. n INOM is stated in contracts. Periods must also be given, e. g. 8% Quarterly or 8% Daily interest. n Periodic rate (IPER) – amount of interest charged each period, e. g. monthly or quarterly. n IPER = INOM / M, where M is the number of compounding periods per year. M = 4 for quarterly and M = 12 for monthly compounding. 29
Classifications of interest rates n Nominal rate (INOM) – also called the quoted or state rate. An annual rate that ignores compounding effects. n INOM is stated in contracts. Periods must also be given, e. g. 8% Quarterly or 8% Daily interest. n Periodic rate (IPER) – amount of interest charged each period, e. g. monthly or quarterly. n IPER = INOM / M, where M is the number of compounding periods per year. M = 4 for quarterly and M = 12 for monthly compounding. 29
 Classifications of interest rates n Effective (or equivalent) annual rate (EAR = EFF%) – the annual rate of interest actually being earned, accounting for compounding. n EFF% for 10% semiannual investment EFF% = ( 1 + INOM / M )M - 1 = ( 1 + 0. 10 / 2 )2 – 1 = 10. 25% n Should be indifferent between receiving 10. 25% annual interest and receiving 10% interest, compounded semiannually. 30
Classifications of interest rates n Effective (or equivalent) annual rate (EAR = EFF%) – the annual rate of interest actually being earned, accounting for compounding. n EFF% for 10% semiannual investment EFF% = ( 1 + INOM / M )M - 1 = ( 1 + 0. 10 / 2 )2 – 1 = 10. 25% n Should be indifferent between receiving 10. 25% annual interest and receiving 10% interest, compounded semiannually. 30
 Why is it important to consider effective rates of return? n Investments with different compounding intervals provide different effective returns. n To compare investments with different compounding intervals, you must look at their effective returns (EFF% or EAR). n See how the effective return varies between investments with the same nominal rate, but different compounding intervals. EARANNUAL EARQUARTERLY EARMONTHLY EARDAILY (365) 10. 00% 10. 38% 10. 47% 10. 52% 31
Why is it important to consider effective rates of return? n Investments with different compounding intervals provide different effective returns. n To compare investments with different compounding intervals, you must look at their effective returns (EFF% or EAR). n See how the effective return varies between investments with the same nominal rate, but different compounding intervals. EARANNUAL EARQUARTERLY EARMONTHLY EARDAILY (365) 10. 00% 10. 38% 10. 47% 10. 52% 31
 When is each rate used? n INOM written into contracts, quoted by banks and brokers. Not used in calculations or shown on time lines. n IPER Used in calculations and shown on time lines. If M = 1, INOM = IPER = EAR. n EAR Used to compare returns on investments with different payments per year. Used in calculations when annuity payments don’t match compounding periods. 32
When is each rate used? n INOM written into contracts, quoted by banks and brokers. Not used in calculations or shown on time lines. n IPER Used in calculations and shown on time lines. If M = 1, INOM = IPER = EAR. n EAR Used to compare returns on investments with different payments per year. Used in calculations when annuity payments don’t match compounding periods. 32
 FV and PV with non-annual interest compounding n = number of years m = number of times interest is paid per year inom = stated annual rate (APR) inom /m = periodic rate Single CF FVnm = PV(1 + inom/m)nm PV = FVnm/(1 + inom/m)nm Annuities: n Use periodic rate and number of annuity payment and compounding periods if interest compounding period annuity payment period are the same. n Otherwise, need to find effective interest rate for each annuity payment period. n n 33
FV and PV with non-annual interest compounding n = number of years m = number of times interest is paid per year inom = stated annual rate (APR) inom /m = periodic rate Single CF FVnm = PV(1 + inom/m)nm PV = FVnm/(1 + inom/m)nm Annuities: n Use periodic rate and number of annuity payment and compounding periods if interest compounding period annuity payment period are the same. n Otherwise, need to find effective interest rate for each annuity payment period. n n 33
 What is the FV of $100 after 3 years under 10% semiannual compounding? Quarterly compounding? 34
What is the FV of $100 after 3 years under 10% semiannual compounding? Quarterly compounding? 34
 Futurama Value Revisited n How much money would Fry have in his bank account in the year 3000 from the $0. 93 deposited in the year 2000 if the 2. 25% annual rate was compounded quarterly? 35
Futurama Value Revisited n How much money would Fry have in his bank account in the year 3000 from the $0. 93 deposited in the year 2000 if the 2. 25% annual rate was compounded quarterly? 35
 Let’s buy a car! n Prof. Outback decides to purchase a brand-new 2007 Jeep Liberty Limited 4 WD with heated premium leather seats, sunroof, and satellite radio for $28, 800. After paying tax and license, Prof. Outback has $4, 000 as a down payment. Jeep offers Prof the choice of 3. 9% APR financing for 60 months or a $3, 000 rebate. Prof. Outback can receive 6. 25% APR financing for 60 months through E-Loan if the rebate option is selected. n n Which option would result in the lower monthly payment? At what APR along without the rebate would the Prof. be indifferent between the two options? 36
Let’s buy a car! n Prof. Outback decides to purchase a brand-new 2007 Jeep Liberty Limited 4 WD with heated premium leather seats, sunroof, and satellite radio for $28, 800. After paying tax and license, Prof. Outback has $4, 000 as a down payment. Jeep offers Prof the choice of 3. 9% APR financing for 60 months or a $3, 000 rebate. Prof. Outback can receive 6. 25% APR financing for 60 months through E-Loan if the rebate option is selected. n n Which option would result in the lower monthly payment? At what APR along without the rebate would the Prof. be indifferent between the two options? 36
 Monthly Payments 37
Monthly Payments 37
 Indifference APR 38
Indifference APR 38


