47f61ea350c28ed12ca3f656f4a488b3.ppt
- Количество слайдов: 73

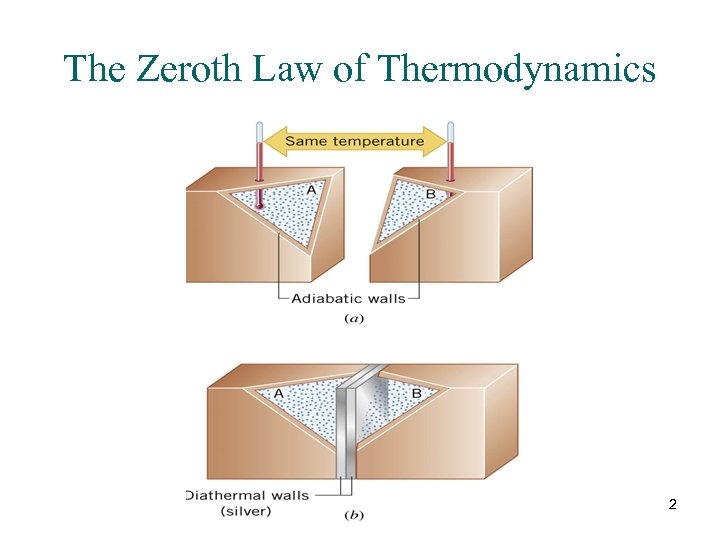
Ch 15. Thermodynamics is the branch of physics that is built upon the fundamental laws that heat and work obey. In thermodynamics the collection of objects on which attention is being focused is called the system, while everything else in the environment is called the surroundings. The system and its surroundings are separated by walls of some kind. Walls that permit heat to flow through them, such as those of the engine block, are called diathermal walls. Perfectly insulating walls that do not permit heat to flow between the system and its surroundings are known as adiabatic walls. 1
The Zeroth Law of Thermodynamics 2

Thermal equilibrium: Two systems are said to be in thermal equilibrium if there is no net flow of heat between them when they are brought into thermal contact. Temperature is the indicator of thermal equilibrium in the sense that there is no net flow of heat between two systems in thermal contact that have the same temperature. THE ZEROTH LAW OF THERMODYNAMICS Two systems individually in thermal equilibrium with a third system* are in thermal equilibrium with each other. 3
The First Law of Thermodynamics 4

THE FIRST LAW OF THERMODYNAMICS The internal energy of a system changes from an initial value Ui to a final value of Uf due to heat Q and work. Q is positive when the system gains heat and negative when it loses heat. W is positive when work is done by the system and negative when work is done on the system. 5
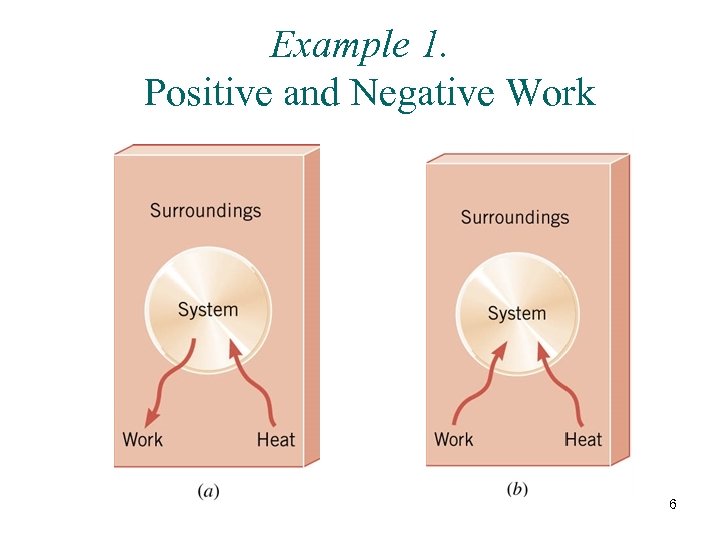
Example 1. Positive and Negative Work 6

The figure illustrates a system and its surroundings. In part a, the system gains 1500 J of heat from its surroundings, and 2200 J of work is done by the system on the surroundings. In part b, the system also gains 1500 J of heat, but 2200 J of work is done on the system by the surroundings. In each case, determine the change in the internal energy of the system. (a) (b) 7

Example 2. An Ideal Gas The temperature of three moles of a monatomic ideal gas is reduced from Ti = 540 K to Tf = 350 K by two different methods. In the first method 5500 J of heat flows into the gas, while in the second, 1500 J of heat flows into it. In each case find (a) the change in the internal energy and (b) the work done by the gas. (a) (b) 8

Check Your Understanding 1 A gas is enclosed within a chamber that is fitted with a frictionless piston. The piston is then pushed in, thereby compressing the gas. Which statement below regarding this process is consistent with the first law of thermodynamics? a. The internal energy of the gas will increase. b. The internal energy of the gas will decrease. c. The internal energy of the gas will not change. d. The internal energy of the gas may increase, decrease, or remain the same, depending on the amount of heat the gas gains or loses. (d) 9

Thermal Processes quasi-static means that it occurs slowly enough that a uniform pressure and temperature exist throughout all regions of the system at all times. An isobaric process is one that occurs at constant pressure. 10
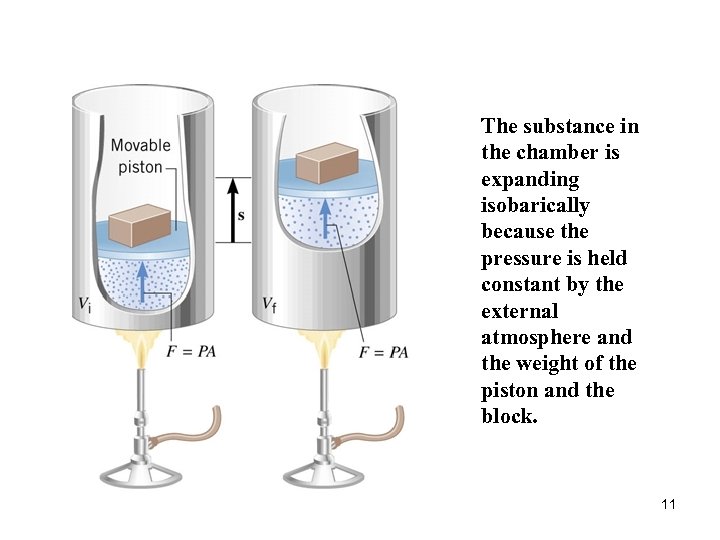
The substance in the chamber is expanding isobarically because the pressure is held constant by the external atmosphere and the weight of the piston and the block. 11

Example 3. Isobaric Expansion of Water One gram of water is placed in the cylinder in above figure, and the pressure is maintained at 2. 0 × 105 Pa. The temperature of the water is raised by 31 C°. In one case, the water is in the liquid phase and expands by the small amount of 1. 0 × 10– 8 m 3. In another case, the water is in the gas phase and expands by the much greater amount of 7. 1 × 10– 5 m 3. For the water in each case, find (a) the work done and (b) the change in the internal energy. c = 4186 J/(kg·C°) c. P = 2020 J/(kg·C°). 12

(a) (b) 13
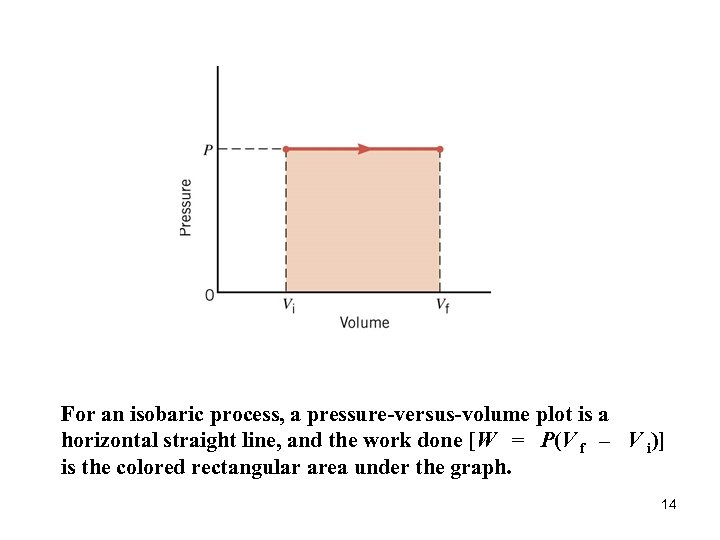
For an isobaric process, a pressure-versus-volume plot is a horizontal straight line, and the work done [W = P(V f – V i)] is the colored rectangular area under the graph. 14
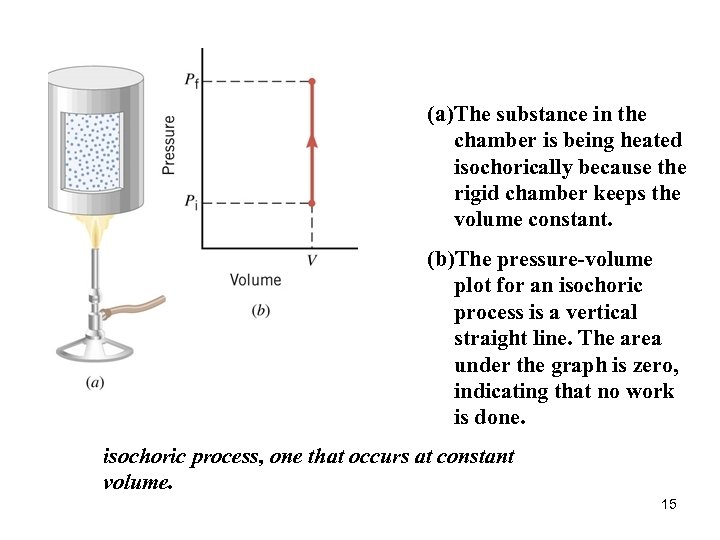
(a) The substance in the chamber is being heated isochorically because the rigid chamber keeps the volume constant. (b)The pressure-volume plot for an isochoric process is a vertical straight line. The area under the graph is zero, indicating that no work is done. isochoric process, one that occurs at constant volume. 15

isothermal process, one that takes place at constant temperature. (when the system is an ideal gas. ) There is adiabatic process, one that occurs without the transfer of heat. Since there is no heat transfer, Q equals zero, and the first law indicates that U = Q – W = –W. Thus, when work is done by a system adiabatically, W is positive and the internal energy of the system decreases by exactly the amount of the work done. When work is done on a system adiabatically, W is negative and the internal energy increases correspondingly. 16
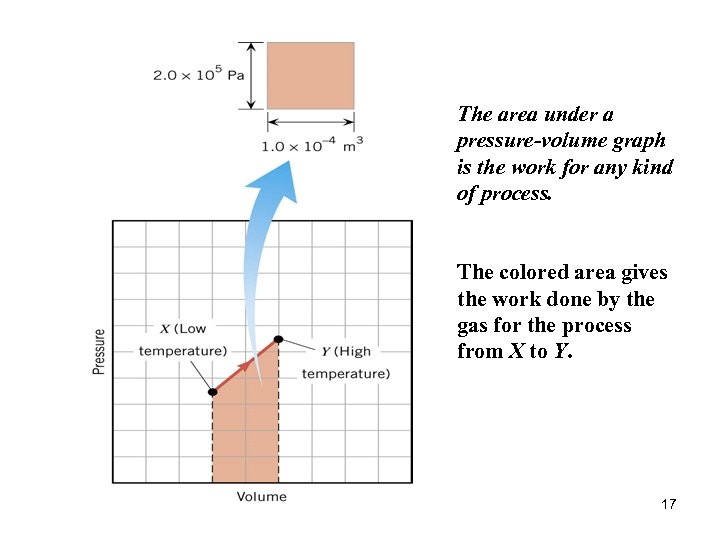
The area under a pressure-volume graph is the work for any kind of process. The colored area gives the work done by the gas for the process from X to Y. 17
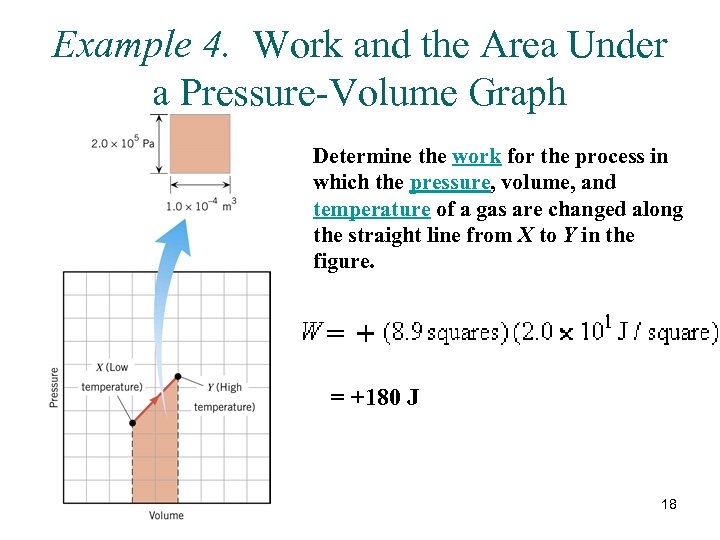
Example 4. Work and the Area Under a Pressure-Volume Graph Determine the work for the process in which the pressure, volume, and temperature of a gas are changed along the straight line from X to Y in the figure. = +180 J 18

Check Your Understanding 2 The drawing shows a pressure-versusvolume plot for a three -step process: A to B, B to C, and C to A. For each step, the work can be positive, negative, or zero. Which answer below correctly describes the work for the three steps? 19

A B B C C A a. Positive Negative b. Positive c. Negative Positive d. Positive e. Negative Positive Negative Zero (b) 20
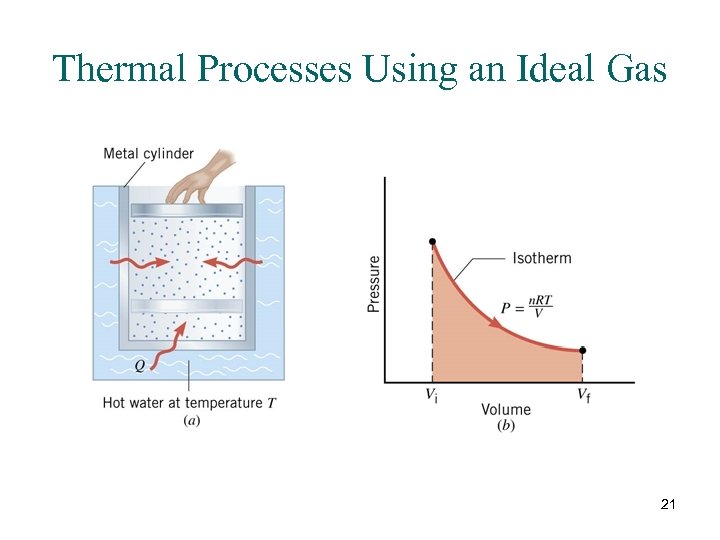
Thermal Processes Using an Ideal Gas 21

ISOTHERMAL EXPANSION OR COMPRESSION P = n. RT/V W = P DV = P(Vf – Vi) 22

Example 5. Isothermal Expansion of an Ideal Gas Two moles of the monatomic gas argon expand isothermally at 298 K, from an initial volume of Vi = 0. 025 m 3 to a final volume of Vf = 0. 050 m 3. Assuming that argon is an ideal gas, find (a) the work done by the gas, (b) the change in the internal energy of the gas, and (c) the heat supplied to the gas. . (a) (b) (c) 23

ADIABATIC EXPANSION OR COMPRESSION 24
![[Ti = Pi. Vi/(n. R)] [Tf = Pf. Vf/(n. R)]. 25 [Ti = Pi. Vi/(n. R)] [Tf = Pf. Vf/(n. R)]. 25](https://present5.com/presentation/47f61ea350c28ed12ca3f656f4a488b3/image-25.jpg)
[Ti = Pi. Vi/(n. R)] [Tf = Pf. Vf/(n. R)]. 25

Type of Thermal Process Work Done First Law of Thermodynamics (DU = Q – W) Isobaric (constant pressure) W = P(Vf – Vi) Isochoric (constant volume) W = 0 J (for an ideal gas) (for a monatomic ideal gas) Isothermal (constant temperature) Adiabatic (no heat flow) 26

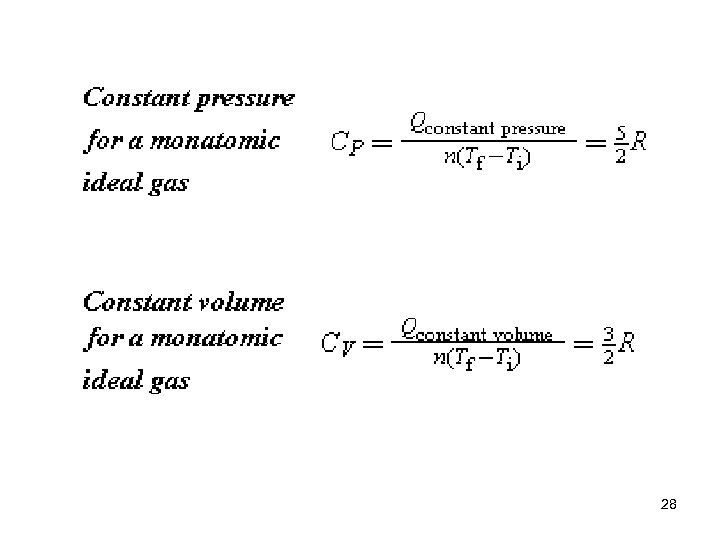
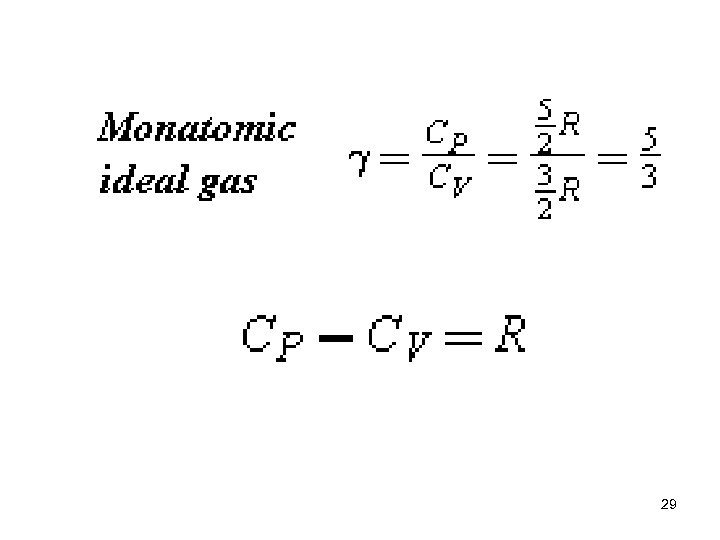
Specific Heat Capacities where the capital letter C refers to the molar specific heat capacity in units of J/(mol·K). 27
28
29

The Second Law of Thermodynamics THE SECOND LAW OF THERMODYNAMICS: THE HEAT FLOW STATEMENT Heat flows spontaneously from a substance at a higher temperature to a substance at a lower temperature and does not flow spontaneously in the reverse direction. 30
31

Heat Engines A heat engine is any device that uses heat to perform work. It has three essential features: 1. Heat is supplied to the engine at a relatively high input temperature from a place called the hot reservoir. 2. Part of the input heat is used to perform work by the working substance of the engine, which is the material within the engine that actually does the work (e. g. , the gasoline-air mixture in an automobile engine). 3. The remainder of the input heat is rejected to a place called the cold reservoir, which has a temperature lower than the input temperature. 32
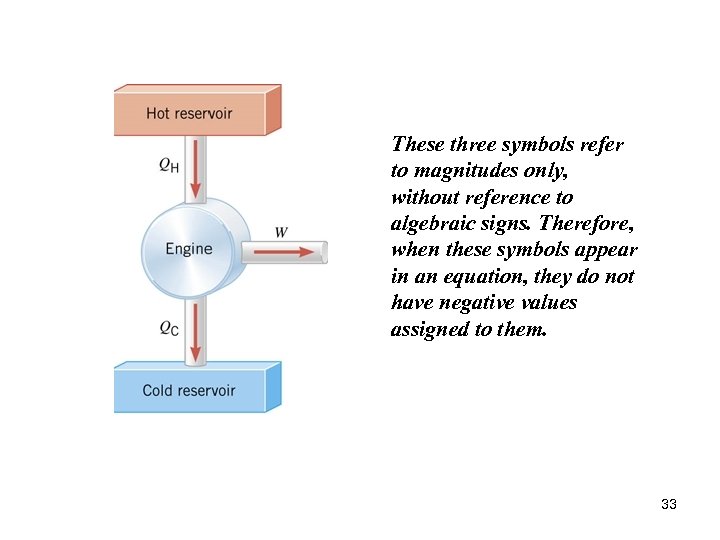
These three symbols refer to magnitudes only, without reference to algebraic signs. Therefore, when these symbols appear in an equation, they do not have negative values assigned to them. 33

Efficiencies are often quoted as percentages obtained by multiplying the ratio W/QH by a factor of 100. 34

Example 6. An Automobile Engine An automobile engine has an efficiency of 22. 0% and produces 2510 J of work. How much heat is rejected by the engine? 35

Carnot's Principle and the Carnot Engine A reversible process is one in which both the system and its environment can be returned to exactly the states they were in before the process occurred. CARNOT’S PRINCIPLE: AN ALTERNATIVE STATEMENT OF THE SECOND LAW OF THERMODYNAMICS No irreversible engine operating between two reservoirs at constant temperatures can have a greater efficiency than a reversible engine operating between the same temperatures. Furthermore, all reversible engines operating between the same temperatures have the same efficiency. 36
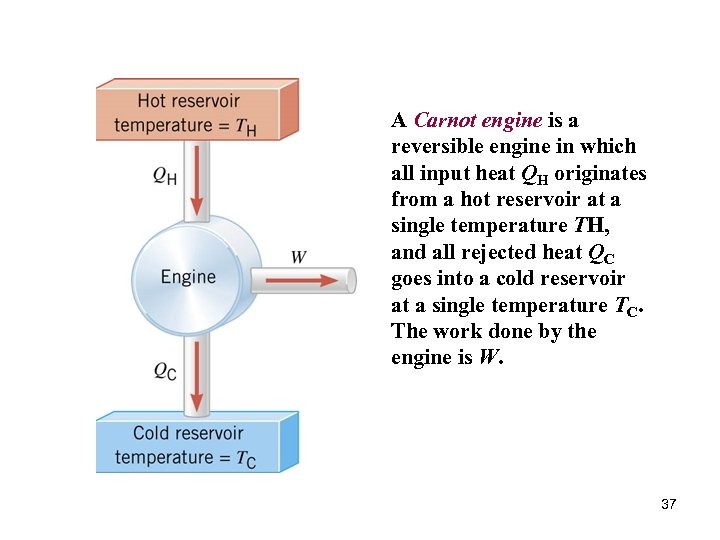
A Carnot engine is a reversible engine in which all input heat QH originates from a hot reservoir at a single temperature TH, and all rejected heat QC goes into a cold reservoir at a single temperature TC. The work done by the engine is W. 37

where the temperatures TC and TH must be expressed in kelvins. 38

Example 7. A Tropical Ocean as a Heat Engine Water near the surface of a tropical ocean has a temperature of 298. 2 K (25. 0 °C), whereas water 700 m beneath the surface has a temperature of 280. 2 K (7. 0 °C). It has been proposed that the warm water be used as the hot reservoir and the cool water as the cold reservoir of a heat engine. Find the maximum possible efficiency for such an engine. TH = 298. 2 K and TC = 280. 2 K 39

Conceptual Example 8. Limits on the Efficiency of a Heat Engine Consider a hypothetical engine that receives 1000 J of heat as input from a hot reservoir and delivers 1000 J of work, rejecting no heat to a cold reservoir whose temperature is above 0 K. Decide whether this engine violates the first or the second law of thermodynamics, or both. It is the second law, not the first law, that limits the efficiencies of heat engines to values less than 100%. 40

Refrigerators, Air Conditioners, and Heat Pumps In the refrigeration process, work W is used to remove heat QC from the cold reservoir and deposit heat QH into the hot reservoir. 41
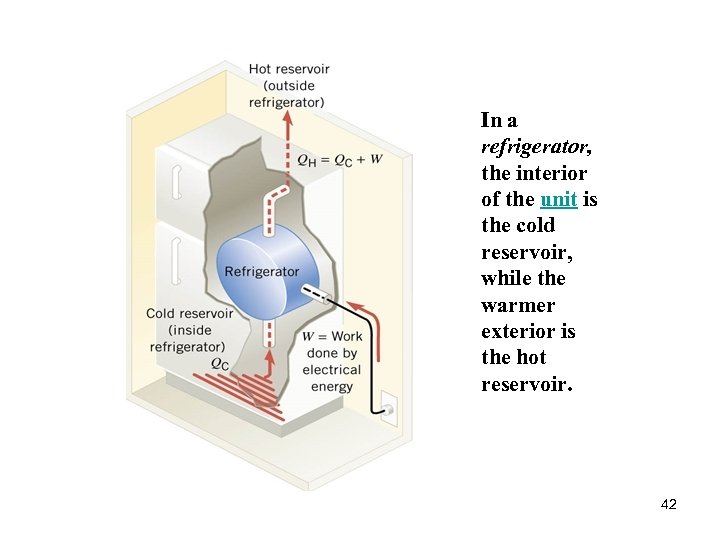
In a refrigerator, the interior of the unit is the cold reservoir, while the warmer exterior is the hot reservoir. 42
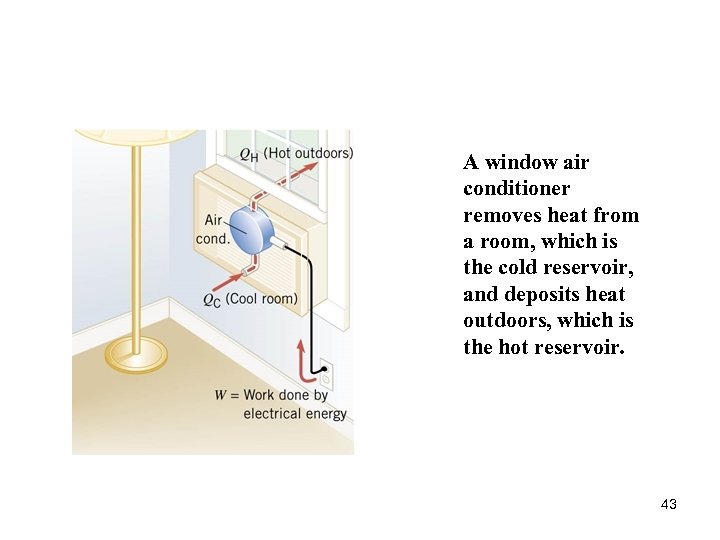
A window air conditioner removes heat from a room, which is the cold reservoir, and deposits heat outdoors, which is the hot reservoir. 43

Conceptual Example 9. You Can’t Beat the Second Law of Thermodynamics Is it possible to cool your kitchen by leaving the refrigerator door open or cool your bedroom by putting a window air conditioner on the floor by the bed? Rather than cooling the kitchen, the open refrigerator warms it up. The air conditioner actually warms the bedroom. 44

45
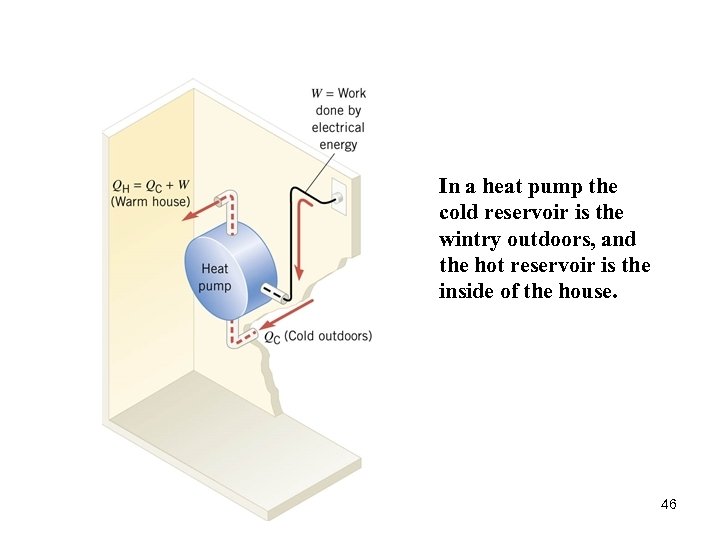
In a heat pump the cold reservoir is the wintry outdoors, and the hot reservoir is the inside of the house. 46
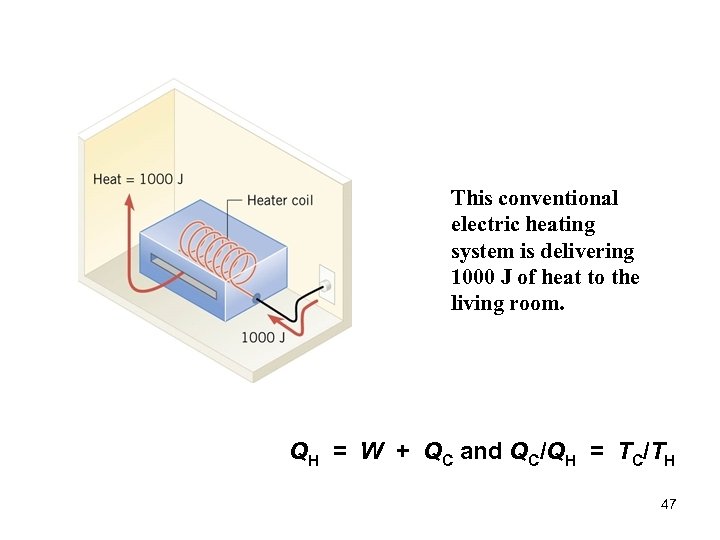
This conventional electric heating system is delivering 1000 J of heat to the living room. QH = W + QC and QC/QH = TC/TH 47

Example 10. A Heat Pump An ideal or Carnot heat pump is used to heat a house to a temperature of TH = 294 K (21 °C). How much work must be done by the pump to deliver QH = 3350 J of heat into the house when the outdoor temperature TC is (a) 273 K (0 °C) and (b) 252 K (– 21 °C)? (a) (b) 48

49
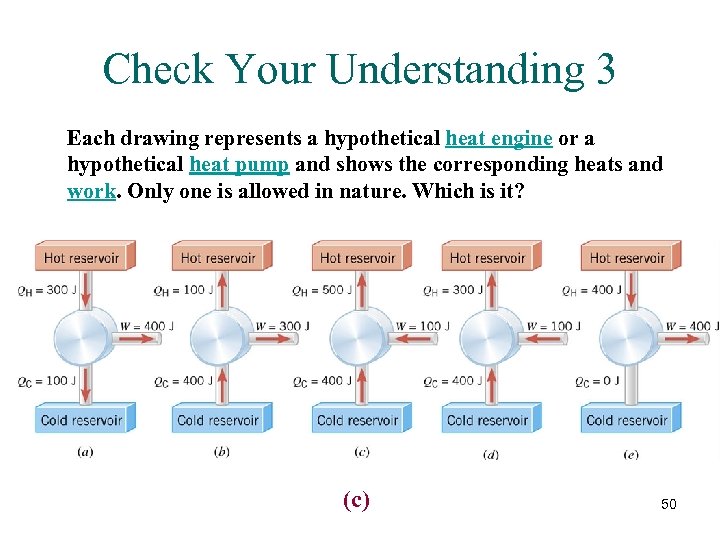
Check Your Understanding 3 Each drawing represents a hypothetical heat engine or a hypothetical heat pump and shows the corresponding heats and work. Only one is allowed in nature. Which is it? (c) 50

Entropy In general, irreversible processes cause us to lose some, but not necessarily all, of the ability to perform work. This partial loss can be expressed in terms of a concept called entropy. Reversible processes do not alter the total entropy of the universe. 51
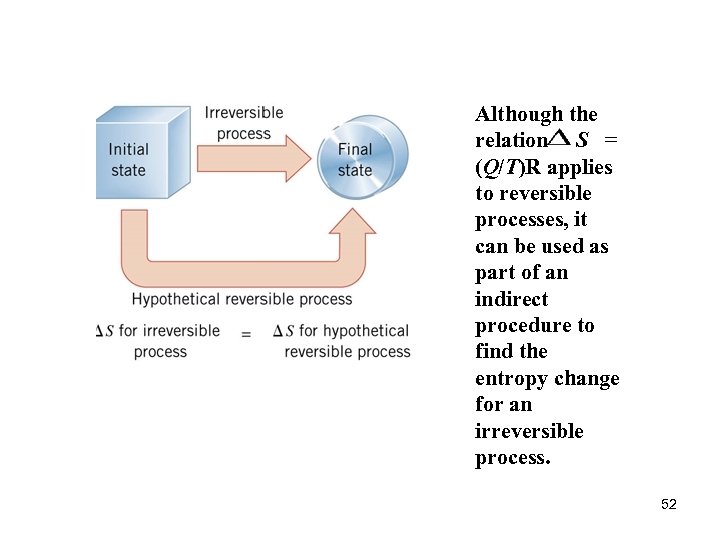
Although the relation S = (Q/T)R applies to reversible processes, it can be used as part of an indirect procedure to find the entropy change for an irreversible process. 52

Example 11. The Entropy of the Universe Increases 1200 J of heat flow spontaneously through a copper rod from a hot reservoir at 650 K to a cold reservoir at 350 K. Determine the amount by which this irreversible process changes the entropy of the universe, assuming that no other changes occur. 53
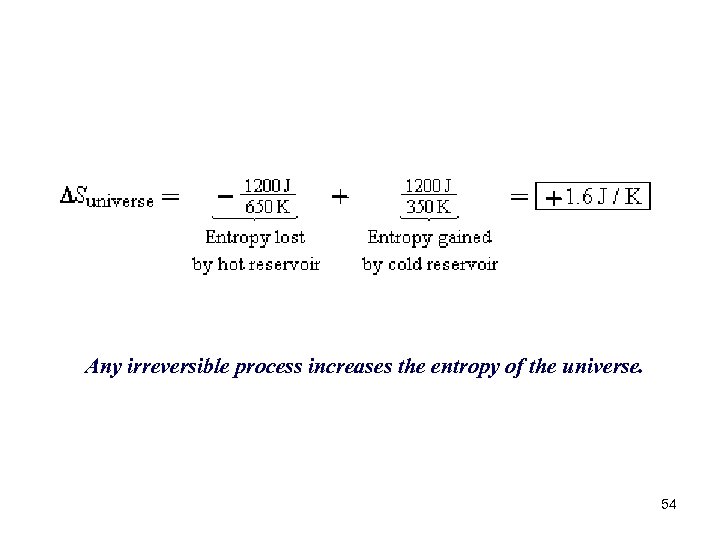
Any irreversible process increases the entropy of the universe. 54

THE SECOND LAW OF THERMODYNAMICS STATED IN TERMS OF ENTROPY The total entropy of the universe does not change when a reversible process occurs ( Suniverse = 0 J/K) and does increases when an irreversible process occurs ( Suniverse > 0 J/K). 55
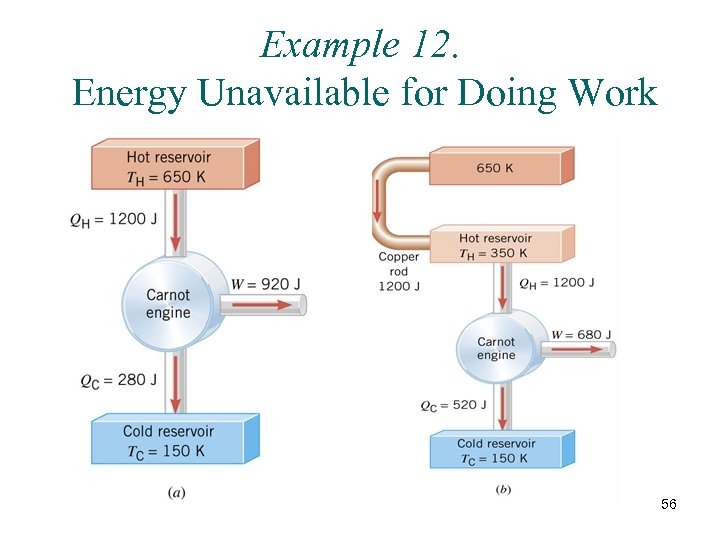
Example 12. Energy Unavailable for Doing Work 56

Suppose that 1200 J of heat is used as input for an engine under two different conditions. In Figure part a the heat is supplied by a hot reservoir whose temperature is 650 K. In part b of the drawing, the heat flows irreversibly through a copper rod into a second reservoir whose temperature is 350 K and then enters the engine. In either case, a 150 -K reservoir is used as the cold reservoir. For each case, determine the maximum amount of work that can be obtained from the 1200 J of heat. 57

where T 0 is the Kelvin temperature of the coldest heat reservoir. 58
A block of ice is an example of an ordered system relative to a puddle of water. 59

Example 13. Order to Disorder Find the change in entropy that results when a 2. 3 -kg block of ice melts slowly (reversibly) at 273 K (0 °C). 60

Check Your Understanding 4 Two equal amounts of water are mixed together in an insulated container. The initial temperatures of the water are different, but the mixture reaches a uniform temperature. Do the energy and the entropy of the water increase, decrease, or remain constant as a result of the mixing process? (d) Energy of the Water Entropy of the Water a. Increases b. Decreases c. Remains constant Decreases d. Remains constant Increases 61

The Third Law of Thermodynamics THE THIRD LAW OF THERMODYNAMICS It is not possible to lower the temperature of any system to absolute zero (T = 0 K) in a finite number of steps. 62

Concepts & Calculations Example 14. The Sublimation of Zinc The sublimation of zinc (mass per mole = 0. 0654 kg/mol) occurs at a temperature of 6. 00 × 102 K, and the latent heat of sublimation is 1. 99 × 106 J/kg. The pressure remains constant during the sublimation. Assume that the zinc vapor can be treated as a monatomic ideal gas and that the volume of solid zinc is negligible compared to the corresponding vapor. What is the change in the internal energy of the zinc when 1. 50 kg of zinc sublimates? Q = DU + W, Q = m. Ls, W = n. RT 63
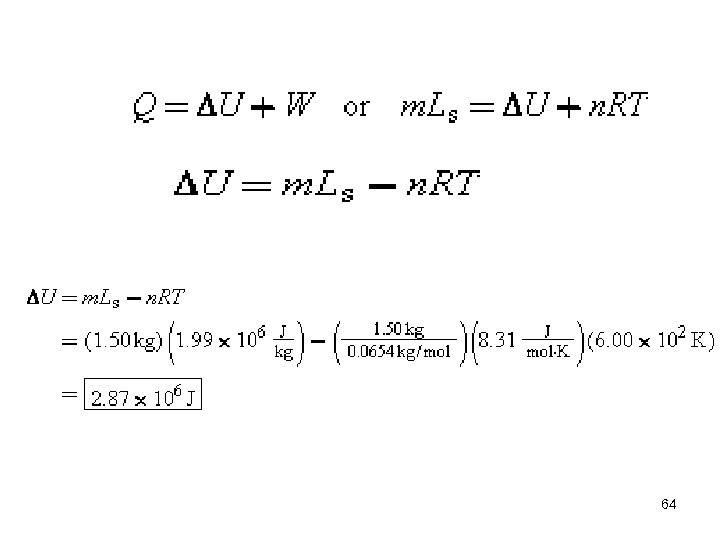
64
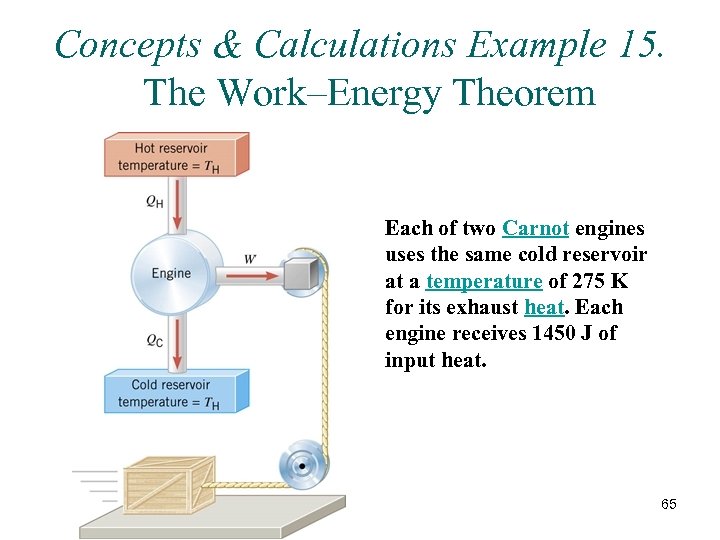
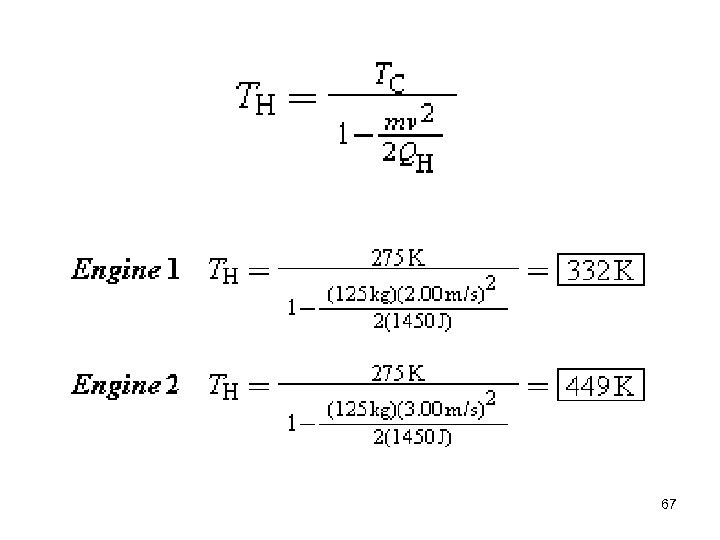
Concepts & Calculations Example 15. The Work–Energy Theorem Each of two Carnot engines uses the same cold reservoir at a temperature of 275 K for its exhaust heat. Each engine receives 1450 J of input heat. 65

The work from either of these engines is used to drive a pulley arrangement that uses a rope to accelerate a 125 -kg crate from rest along a horizontal frictionless surface. With engine 1 the crate attains a speed of 2. 00 m/s, while with engine 2 it attains a speed of 3. 00 m/s. Find the temperature of the hot reservoir for each engine. 66
67

Conceptual Question 14 REASONING AND SOLUTION The efficiency of a Carnot engine is given by Equation 15. 15 . Three reversible engines A, B, and C, use the same cold reservoir for their exhaust heats. They use different hot reservoirs with the following temperatures: (A) 1000 K; (B) 1100 K; and (C) 900 K. We can rank these engines in order of increasing efficiency according to the following considerations. The ratio is inversely proportional to the value of TH. The ratio will be smallest for engine B; therefore, the quantity 1 – will be largest for engine B. Thus, engine B has the largest efficiency. Similarly, the ratio will be largest for engine C; therefore, the quantity 1 – will be smallest for engine C. Thus, engine C has the smallest efficiency. Hence, the engines are, in order of increasing efficiency: engine C, engine A, and engine B. 68

Conceptual Question 15 REASONING AND SOLUTION The efficiency of a Carnot engine is given by Equation 15. 15: a. Lowering the Kelvin temperature of the cold reservoir by a factor of four makes the ratio one-fourth as great. b. Raising the Kelvin temperature of the hot reservoir by a factor of four makes the ratio one-fourth as great. c. Cutting the Kelvin temperature of the cold reservoir in half and doubling the Kelvin temperature of the hot reservoir makes the ratio one-fourth as great. Therefore, all three possible improvements have the same effect on the efficiency of a Carnot engine. 69

Problem 51 REASONING AND SOLUTION The efficiency of the engine is e = 1 - (TC/TH) so (i) Increase TH by 40 K; e = 1 - [(350 K)/(690 K)] = 0. 493 (ii) Decrease TC by 40 K; e = 1 - [(310 K)/(650 K)] = 0. 523 The greatest improvement is made by lowing the temperature of the cold reservoir. 70

Problem 63 REASONING AND SOLUTION Let CP denote the coefficient of performance. By definition (Equation 15. 16), CP = QC/W, so that Thus, the amount of heat that is pumped out of the back of the air conditioner is 71

The temperature rise in the room can be found as follows: QH = CV n T 72

Problem 64 REASONING AND SOLUTION The amount of heat removed from the ice QC is QC = m. Lf = (2. 0 kg)(33. 5 * 104 J/kg) = 6. 7 * 105 J The amount of heat leaving the refrigerator QH is therefore QH = QC(TH/TC) = (6. 7 * 105 J)(300 K)/(258 K) = 7. 8 * 105 J The amount of work done by the refrigerator is therefore, W = QH - QC = 1. 1 * 105 J At $0. 10 per k. Wh (or $0. 10 per 3. 6 * 106 J), the cost is 73
47f61ea350c28ed12ca3f656f4a488b3.ppt