Ч 1 Лекция 2 Булева алгебра и логические

Ч 1. Лекция 2 Булева алгебра и логические элементы Лектор: Люличева И. А. 1

Рассматриваются вопросы n n Булева алгебра и логические функции двух переменных. Законы булевой алгебры. Логические элементы и их условные обозначения. Логические функции нескольких переменных. Синтез и преобразование логических функций. 2

2. 1 Булева алгебра и логические функции 2 -х переменных n n n Для формального описания узлов ЭВМ и других цифровых систем при их анализе и синтезе используется аппарат алгебры логики. Основные положения алгебры логики разработал в 19 веке математик Джордж Буль, поэтому алгебру логики называют также булевой алгеброй. В булевой алгебре различают двоичные переменные и булевы функции. Двоичные переменные могут принимать два значения: 0 и 1. Они называются также логическими или булевыми переменными и обозначаются символами x 1, x 2, x 3, …

2. 1 Булева алгебра и логические функции 2 -х переменных n n Булевы функции как и аргументы, могут принимать лишь два значения: 0 или 1. Булевы функции называют также логическими или переключательными функциями. Будем обозначать логиеские функции в виде f(x 1, x 2, x 3, …) указывая в скобках аргументы, либо в виде y 1, y 2, y 3, … Булевы функции в свою очередь могут служить аргументами еще более сложных логических функций. Следовательно, можно построить переключательные функции любой заранее заданной сложности, пользуясь ограниченным числом логических связей.

2. 1 Булева алгебра и логические функции 2 -х переменных n n n Булевы функции принято задавать таблицами истинности, в которых для всех наборов переменных указываются соответствующие им значения булевых функции. Формирование значений в таблице истинности выполняется в соответствии с логикой работы устройства (мультивибратора, дешифратора, сумматора, сдвигающего регистра, и т. д. ). Рассмотрим сначала простейшие булевы функции.

Булевы функции 2 -х переменных n n Множество всех логических функций двух переменных – бинарные логические операции – представлено в таблице 3. Число всех функций равно числу перестановок из 2 по 4 то есть 16. Таблица 3 6

Булевы функции 2 -х переменных n n n В таблице 3 представлены следующие функции: ψ0, ψ15 – функции констант 0 и 1; ψ1 – повторение х1 (х2 – фиктивная переменная); ψ2 – повторение х2 (х1 – фиктивная переменная); ψ3 – x 1 (х2 – фиктивная переменная); ψ4 – x 2 (х1 – фиктивная переменная); 7

Булевы функции 2 -х переменных n n n ψ5 – х1+х2; х1∨х2 – дизъюнкция (ИЛИ); ψ6 – 1 2 x + x ; х1↓х2 – стрелка Пирса (ИЛИ-НЕ); ψ7 – x 1&x 2; x 1∧x 2; x 1⋅x 2 – конъюнкция (И); ψ8 – штрих Шеффера (И-НЕ); ψ9 – x 1⊕x 2; x 1≡x 2 – сложение по модулю 2 (функция неравнозначности); ψ10 – НЕ x ⊕ x ; x 1~x 2; x 1≡x 2 – эквивалентность, равнозначность, отрицание сложения по модулю 2; 8

Булевы функции 2 -х переменных n n n n ψ11 – x 1→x 2; x 1⊃x 2 – импликация (х1 влечёт за собой х2); ψ12 – 1 2 x → x – отрицание импликант (функция запрета); ψ13 – x 2→x 1; x 2⊃x 1 – импликация (х2 влечёт за собой х1); ψ14 – 2 1 x → x – отрицание импликант (функция запрета). Логические функции трех и более переменных обычно задаются (наряду с таблицами истинности) также формулами, состоящими из символов переменных и знаков унарных и бинарных операций. Значение любой логической формулы, содержащей знаки логических операций, можно вычислить для любого набора значений переменных, используя таблицу 3. Наиболее полезные ЛФ приведены в Таблице 4. 9

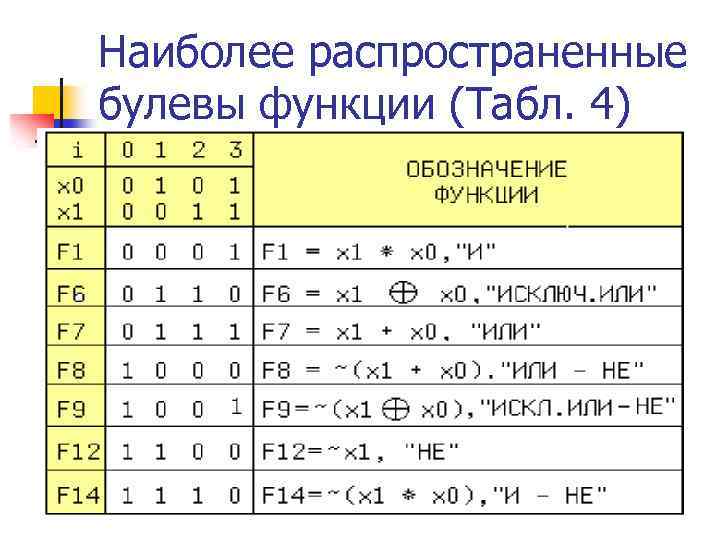
Наиболее распространенные булевы функции (Табл. 4)

2. 2 Законы булевой алгебры n n В булевой алгебре используются четыре основных закона: переместительный, сочетательный, распределительный, инверсии. Эти законы позволяют проводить эквивалентные преобразования логических функций (ЛФ), записанных с помощью операций НЕ, И, ИЛИ, т. е. приводить выражения ЛФ к более простому виду. Рассмотрим некоторые законы.

2. 2 Законы булевой алгебры n 1. Переместительный закон аналогичен n переместительному закону обычной алгебры и записывается в виде: а) для дизъюнкции n б) для конъюнкции n Таким образом: от перемены мест слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

2. 2 Законы булевой алгебры n 2. Сочетательный закон также аналогичен n сочетательному закону обычной алгебры и записывается в виде: а) для дизъюнкции n б) для конъюнкции n Следовательно, можно группировать переменные, объединенные знаком дизъюнкции или конъюнкции, это не меняет значений функции. Имеет смысл для ЛФ 3 и более переменных.

2. 2 Законы булевой алгебры n n n Закон инверсии: а) для дизъюнкции т. е. отрицание суммы логических переменных эквивалентно произведению отрицаний этих переменных; б) для конъюнкции т. е. отрицание произведения переменных эквивалентно сумме отрицаний этих переменных. Справедливость этих выражений доказывается путем составления таблиц истинности для левой и правой частей каждого выражения и их сравнения на совпадение для одних и тех же наборов переменных.

2. 2 Законы булевой алгебры n n n Из законов алгебры логики выводится ряд важных правил, которые полезны при выполнении эквивалентных преобразований 1. Выражения, имеющие всегда значение 1: х+1=1 2. Выражения, имеющие всегда значение 0: х*0=0

2. 2 Законы булевой алгебры 3. Двойное отрицание: NOT (NOT x) = x n 4. Повторение: x AND x = x x OR x = x n 5. Склеивание: .

2. 2 Законы булевой алгебры n n Пример формального сокращения с учётом основных законов: (a and b) or (not a and b) or (a and not b) = ((a and b) or (not a and b)) or (a and not b) = ((a or not a) and b) or (a and not b) = (1 and b) or (a and not b) = b or (a and not b) = a or b

2. 3 Логические элементы n Логический элемент в электронных схемах – это устройство, реализующее ту или иную логическую функцию. При этом логические сигналы 0 и 1 задаются разными уровнями напряжения. Сигнал логического нуля обычно представляется низким уровнем напряжения U 0, логической единицы – высоким U 1. Такая логика получила название положительной. В ряде случаев используют отрицательную логику, где логический нуль представляется высоким уровнем напряжения, а логическая единица – низким. 18

Что такое логические элементы Для изображения логических схем всегда используются условные графические обозначения элементов, описывающие только выполняемую элементами функцию и не зависящие от его схемы. В настоящее время в мире существует несколько общепринятых стандартов условных обозначений. 19

Что такое логические элементы n Наиболее распространенными являются американский стандарт milspec 806 В и стандарт МЭК 117 -15 А, созданный Международной Электротехнической Комиссией. Часто в литературе используются также обозначения в европейской системе DIN 4070. В отечественной литературе условные обозначения элементов в основном соответствуют ГОСТ 2. 743 -82. 20

Основные логические операции и логические элементы Рис. 2. Условные обозначения логического элемента ИЛИ: а) по ГОСТ, б) по стандарту МЭК, в) по стандарту DIN, г) по стандарту milspec 21

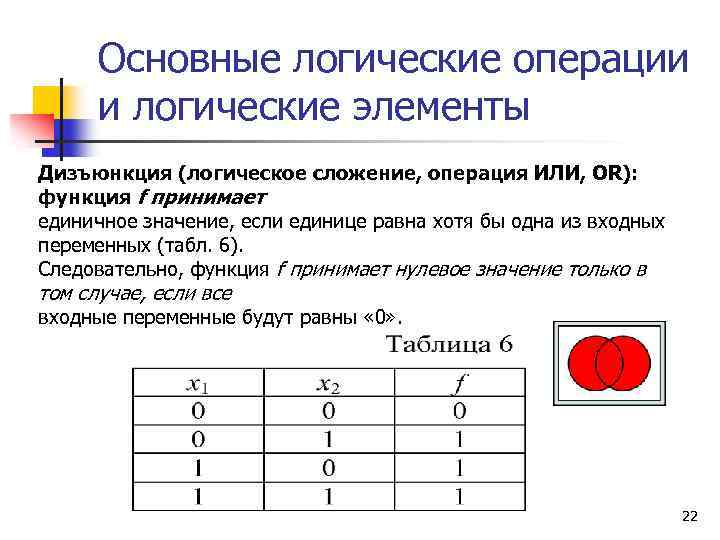
Основные логические операции и логические элементы Дизъюнкция (логическое сложение, операция ИЛИ, OR): функция f принимает единичное значение, если единице равна хотя бы одна из входных переменных (табл. 6). Следовательно, функция f принимает нулевое значение только в том случае, если все входные переменные будут равны « 0» . 22

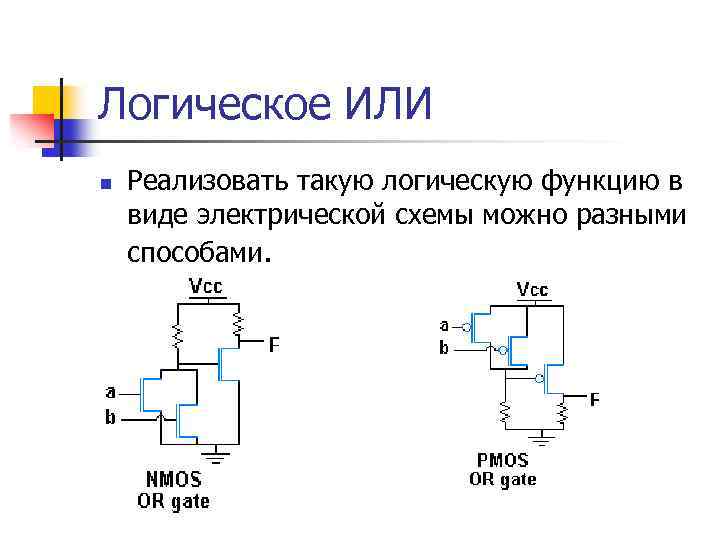
Логическое ИЛИ n Реализовать такую логическую функцию в виде электрической схемы можно разными способами.

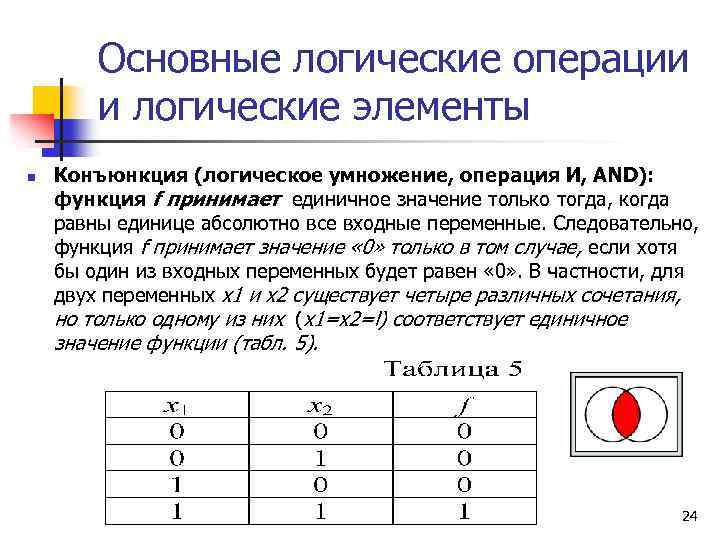
Основные логические операции и логические элементы n Конъюнкция (логическое умножение, операция И, AND): функция f принимает единичное значение только тогда, когда равны единице абсолютно все входные переменные. Следовательно, функция f принимает значение « 0» только в том случае, если хотя бы один из входных переменных будет равен « 0» . В частности, для двух переменных х1 и х2 существует четыре различных сочетания, но только одному из них (х1=х2=l) соответствует единичное значение функции (табл. 5). 24

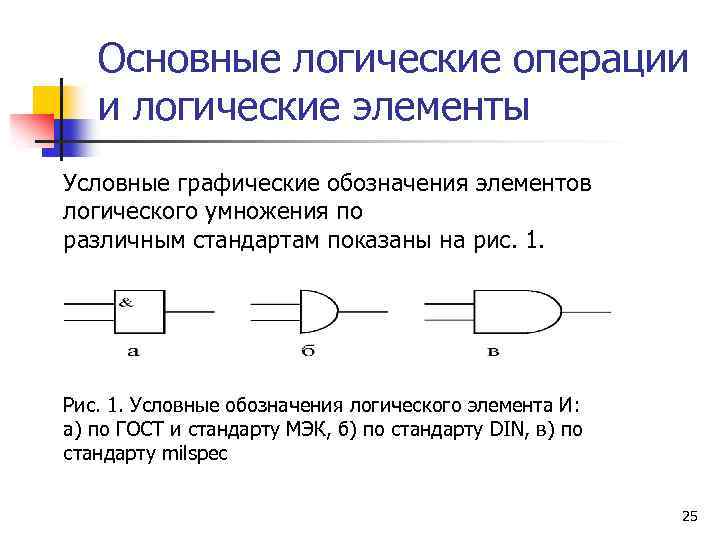
Основные логические операции и логические элементы Условные графические обозначения элементов логического умножения по различным стандартам показаны на рис. 1. Рис. 1. Условные обозначения логического элемента И: а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec 25

Основные логические операции и логические элементы n Инверсия (отрицание, операция НЕ, NOT): функция одной переменной, принимает единичное значение, если входная переменная равна « 0» . Функция равна « 0» , если входная переменная равна « 1» (табл. 7). 26

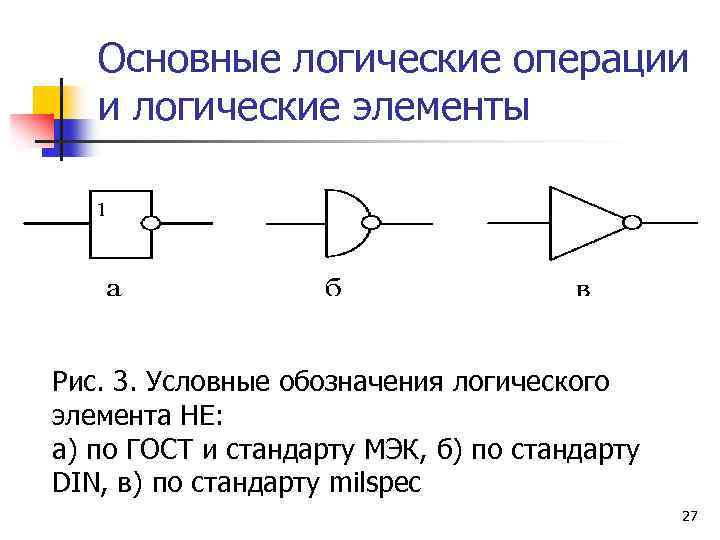
Основные логические операции и логические элементы Рис. 3. Условные обозначения логического элемента НЕ: а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec 27

Реализация логического элемента НЕ

Распространённые логические операции и логические элементы n n Наряду с простейшими распространены и более сложные логические элементы, сочетающие в себе несколько простейших операций. Такими являются логические элементы И-НЕ, ИЛИ-НЕ, ЭКВИВАЛЕНТНОСТЬ, ИСКЛЮЧАЮЩЕЕ ИЛИ и т. п. Штрих Шеффера. Элемент И-НЕ реализует функцию «штрих Шеффера» двух переменных 1 2 f = х ⋅ х и имеет соответствующую таблицу истинности (табл. 3). Условное обозначение логического элемента И-НЕ в любом стандарте объединяет в себе обозначение элемента И и кружок, являющийся признаком элемента НЕ. 30

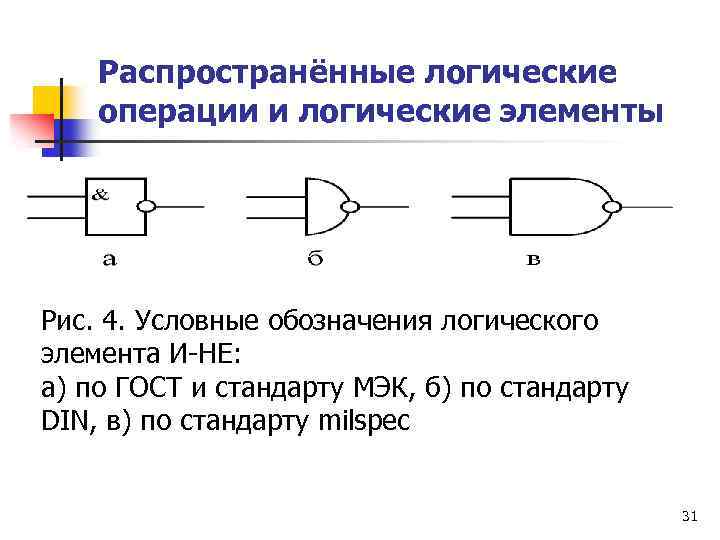
Распространённые логические операции и логические элементы Рис. 4. Условные обозначения логического элемента И-НЕ: а) по ГОСТ и стандарту МЭК, б) по стандарту DIN, в) по стандарту milspec 31

Распространённые логические операции и логические элементы Стрелка Пирса. Элемент ИЛИ-НЕ реализует функцию «стрелка Пирса» : 1 2 f = х ∨ х , описанную в табл. 3. Условные обозначения объединяют в себе обозначение элемента ИЛИ и кружок – символ операции отрицания НЕ(рис. 5). Рис. 5. Условные обозначения логического элемента ИЛИ-НЕ: а) по ГОСТ, б) по стандарту МЭК, в) по стандарту DIN, г) по стандарту milspec 32

Распространённые логические операции и логические элементы Эквивалентность. Элемент ЭКВИВАЛЕНТНОСТЬ (РАВНОЗНАЧНОСТЬ) описывается функцией ψ10 из табл. 3. В ней выходная переменная f принимает единичные значения только при равенстве входных переменных x 1=x 2. Функция имеет собственное обозначение и может быть выражена через простейшие логические операции. Условное обозначение логического элемента ЭКВИВАЛЕНТНОСТЬ 33

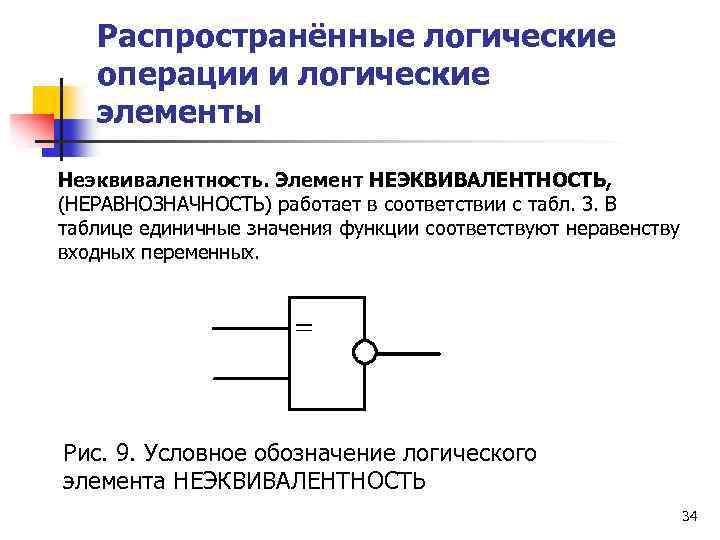
Распространённые логические операции и логические элементы Неэквивалентность. Элемент НЕЭКВИВАЛЕНТНОСТЬ, (НЕРАВНОЗНАЧНОСТЬ) работает в соответствии с табл. 3. В таблице единичные значения функции соответствуют неравенству входных переменных. Рис. 9. Условное обозначение логического элемента НЕЭКВИВАЛЕНТНОСТЬ 34

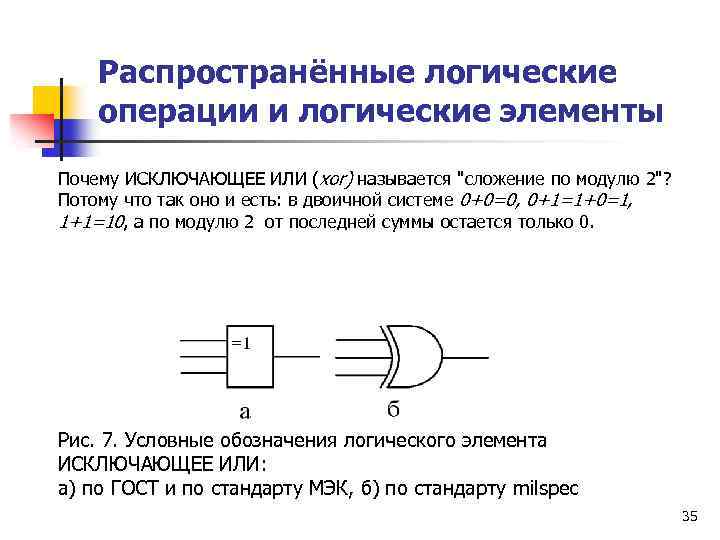
Распространённые логические операции и логические элементы Почему ИСКЛЮЧАЮЩЕЕ ИЛИ (xor) называется "сложение по модулю 2"? Потому что так оно и есть: в двоичной системе 0+0=0, 0+1=1+0=1, 1+1=10, а по модулю 2 от последней суммы остается только 0. Рис. 7. Условные обозначения логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ: а) по ГОСТ и по стандарту МЭК, б) по стандарту milspec 35

Распространённые логические операции и логические элементы Включение функции xor в джентльменский набор вызвано её замечательными свойствами. Во-первых, при инвертировании одного из аргументов эта функция также инвертируется. Во-вторых, эта функция показывает, когда аргументы не равны (а при инвертировании одного из аргументов - когда равны). В-третьих, она позволяет проводить управляемое инвертирование: при нулевом аргументе другой аргумент не меняется, при единичном же значении второй аргумент инвертируется. Наконец, эта функция инволютивна (её повторное применение возвращает к исходному аргументу): если (x 3=x 1 xor x 2), то (x 3 xor x 1=x 2) и (x 3 xor x 2=x 1). 36

2. 4 Логические функции нескольких переменных n n Любая логическая функция нескольких переменных однозначно задается в виде. Таблицы истинности, в левой части которой выписаны все возможные наборы значений её аргументов x 1, …, xn, а правая часть представляет собой столбец значений функций, соответствующих этим наборам. Набор значений переменных, на котором функция принимает значение f = 1, называется единичным набором функции f; множество всех единичных наборов – единичным множеством функции f.

Таблица истинности n n Аналогично набор значений, на котором f = 0, называется нулевым набором функции f, а множество нулевых наборов – нулевым множеством. В общем случае таблица истинности для функции от n переменных должна иметь 2^n строк. Переменная х в функции f называется фиктивной (несущественной), если значение переменной х не влияет на значение булевой функции. Фиктивные переменные могут быть удалены или введены в набор переменных функций. 38

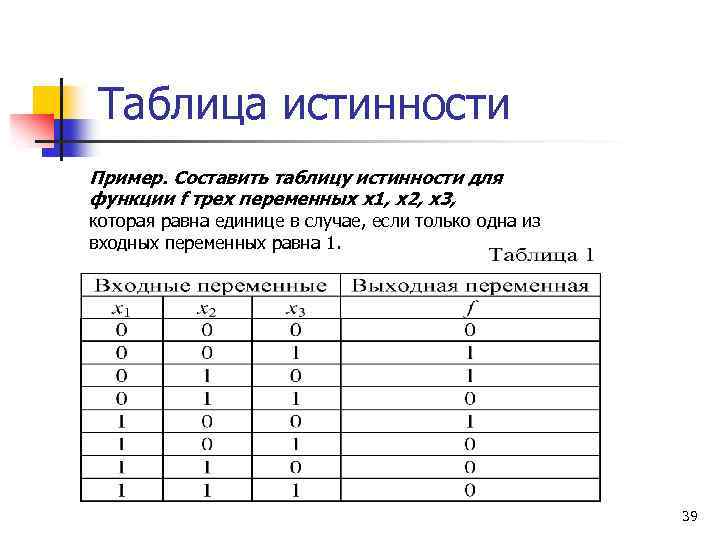
Таблица истинности Пример. Составить таблицу истинности для функции f трех переменных x 1, x 2, x 3, которая равна единице в случае, если только одна из входных переменных равна 1. 39

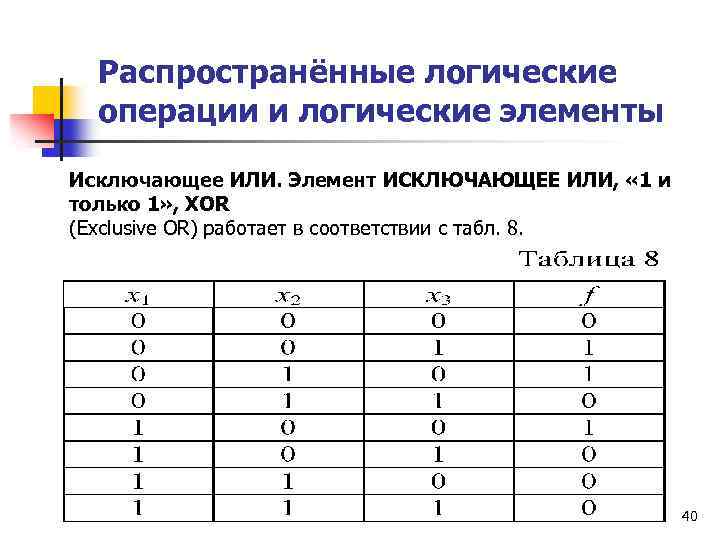
Распространённые логические операции и логические элементы Исключающее ИЛИ. Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, « 1 и только 1» , XOR (Exclusive OR) работает в соответствии с табл. 8. 40

2. 4 Логические функции нескольких переменных В таблице единичные значения функции соответствуют строкам, в которых младший разряд арифметической суммы входных переменных равен 1: f =x 1⊕x 2⊕x 3. Рис. 8. Условное обозначение логического элемента СУММА ПО МОДУЛЮ 2 для 3 переменных. 41

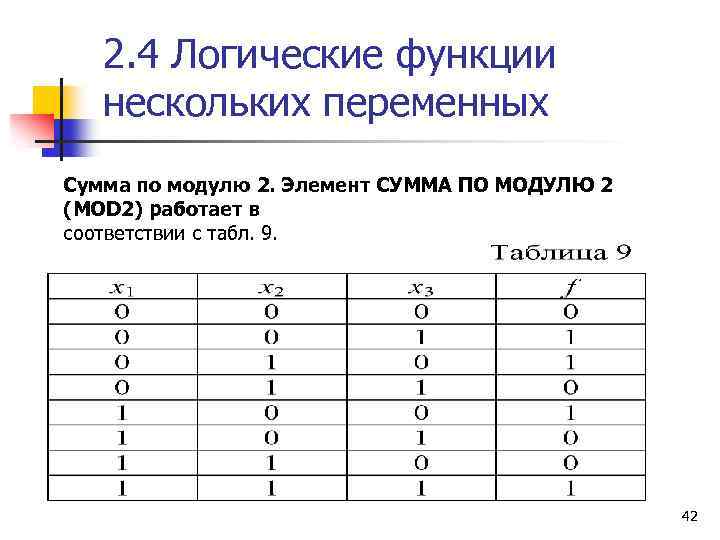
2. 4 Логические функции нескольких переменных Сумма по модулю 2. Элемент СУММА ПО МОДУЛЮ 2 (MOD 2) работает в соответствии с табл. 9. 42

2. 4 Логические функции нескольких переменных n n Существуют также логические функции 4 х и более элементов. Промышленностью выпускается большое количество микросхем для реализации логических функций 2 и более аргументов или НЕСКОЛЬКО простейших функций.

Вопросы для самоконтроля 1. Что такое логические элементы? 2. Что такое булевы функции двух переменных? 3. Перечислите основные логические операции и логические элементы. 4. Приведите таблицу истинности а) И б) ИЛИ в) И-НЕ для 2 х переменных. 5. Какие функции 3 х логических элементов вы знаете? 6. Таблица истинности функции И для 3 х переменных. 44