Centre for Industrial Mathematical Modelling School of Mathematical

Centre for Industrial Mathematical Modelling School of Mathematical Sciences

Introduction Industry faces many mathematicallychallenging problems – Simulation of large complex systems (e. g. electromagnetic compatibility in high speed electrical systems) – Pattern recognition and image analysis problems (e. g. face recognition, signal analysis) – Optimization of industrial processes (e. g. separation technologies in the oil and chemical industries) – Modelling chemically complex systems (e. g. oxidation of polymeric implants)

Introduction Industry faces many mathematicallychallenging problems – Simulation of large complex systems electromagnetic compatibility in high speed electrical systems – Pattern recognition and image analysis problems (e. g. face recognition, signal analysis) – Optimization of industrial processes (e. g. separation technologies in the oil and chemical industries) – Modelling chemically complex systems (e. g. oxidation of polymeric implants)

Introduction Industry faces many mathematicallychallenging problems – Simulation of large complex systems electromagnetic compatibility in high speed electrical systems – Pattern recognition and image analysis problems face recognition, signal analysis – Optimization of industrial processes (e. g. separation technologies in the oil and chemical industries) – Modelling chemically complex systems (e. g. oxidation of polymeric implants)

Introduction Industry faces many mathematicallychallenging problems – Simulation of large complex systems electromagnetic compatibility in high speed electrical systems – Pattern recognition and image analysis problems face recognition, signal analysis – Optimization of industrial processes separation technologies in the oil and chemical industries – Modelling chemically complex systems (e. g. oxidation of polymeric implants)

Introduction Industry faces many mathematicallychallenging problems – Simulation of large complex systems electromagnetic compatibility in high speed electrical systems – Pattern recognition and image analysis problems face recognition, signal analysis – Optimization of industrial processes separation technologies in the oil and chemical industries – Modelling chemically complex systems oxidation of polymeric medical implants

Why Nottingham? 1. In top 5 in UK for industrial funding 2. Interdisciplinary research culture 3. Broad range of mathematical expertise 4. State of the art HPC facility 5. Advanced facilities for experimental investigation and model validation 6. Strong international links

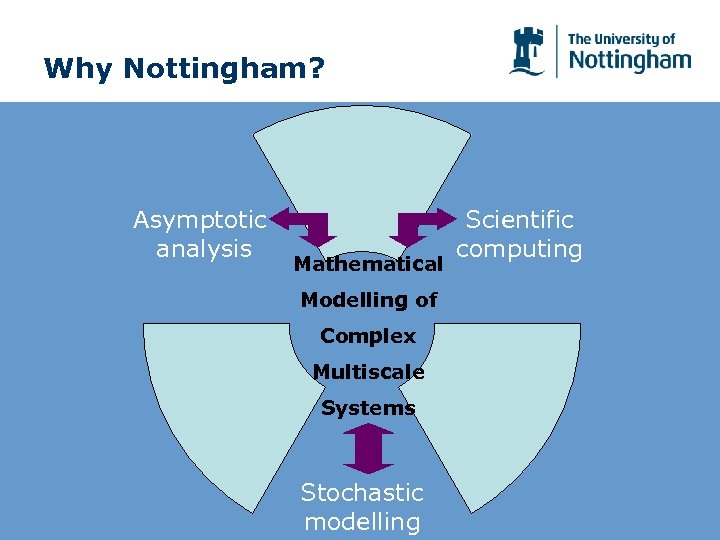Why Nottingham? Asymptotic analysis Mathematical Modelling of Complex Multiscale Systems Stochastic modelling Scientific computing

Track Record • Total of 30 permanent staff in Theoretical Mechanics and Statistics • Past and current collaborations with Engineering Schools and external industry – Rolls Royce University Technology Centre – Unilever, AEA Technology, HSL, Magnox Electric, Qineti. Q, Waltham Pet Centre, … • Existing collaborations with biomedical sciences through the Centre for Mathematical Medicine

Recent Developments • Recent new chairs in Industrial and Computational Mathematics – Billingham, Cliffe, Houston • Closer links between Statistics and Applied Mathematics – Joint supervision of 10 Ph. D students through a Marie Curie Early Stage Training award + 2 existing Ph. D students • University commitment to this proposal – Five new Ph. D studentships – Business Development Officer – Computing time on HPC facility – Office space

Basic Structure • Initially, four projects • Four PDRAs, seven graduate students (five University-funded) • Regular project and inter-project meetings • Regular meetings with industrial project partners • One interdisciplinary conference per year • At least two Visiting Fellows per year • Regular seminar series

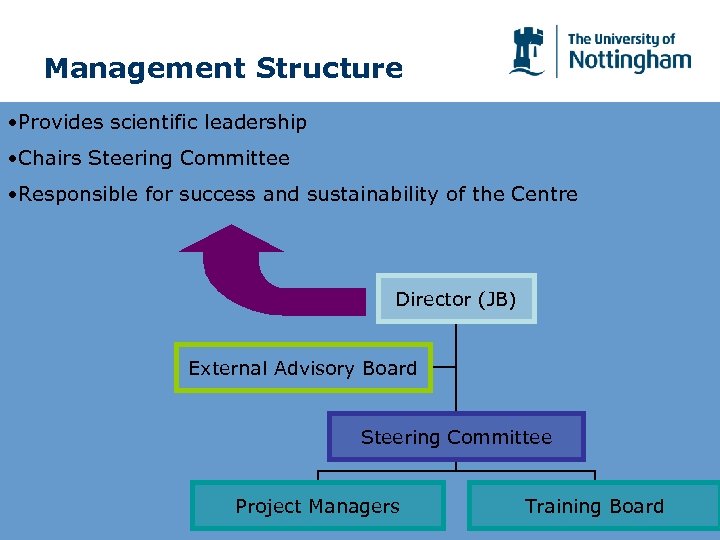Management Structure • Provides scientific leadership • Chairs Steering Committee • Responsible for success and sustainability of the Centre Director (JB) External Advisory Board Steering Committee Project Managers Training Board

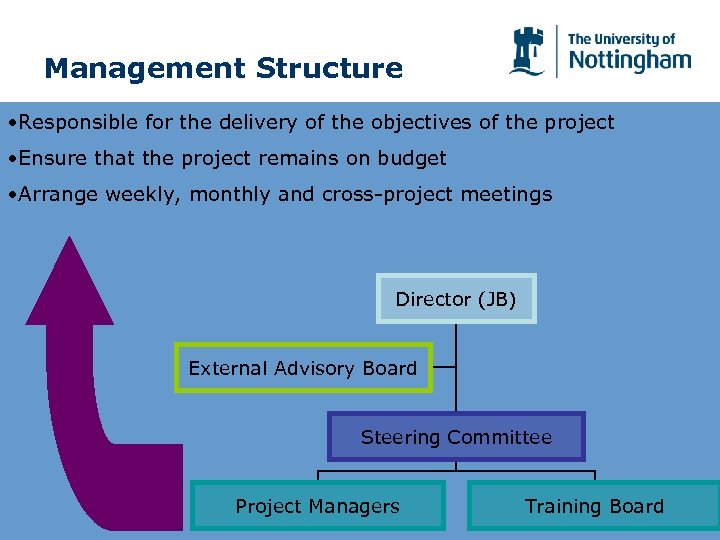Management Structure • Responsible for the delivery of the objectives of the project • Ensure that the project remains on budget • Arrange weekly, monthly and cross-project meetings Director (JB) External Advisory Board Steering Committee Project Managers Training Board

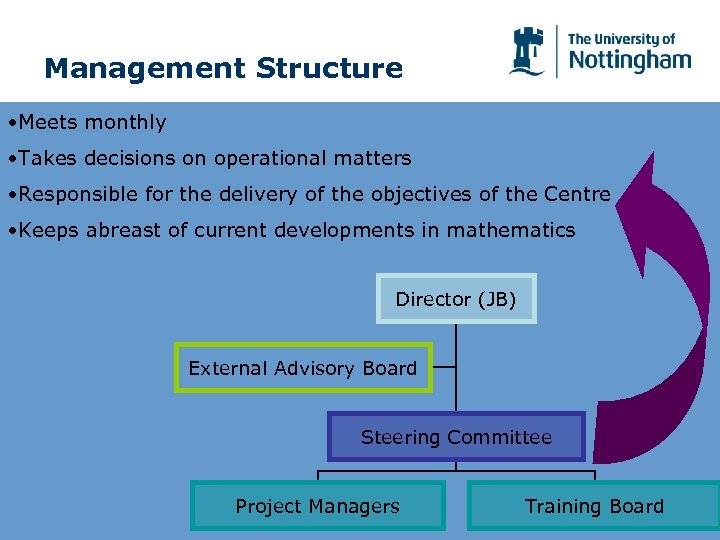Management Structure • Meets monthly • Takes decisions on operational matters • Responsible for the delivery of the objectives of the Centre • Keeps abreast of current developments in mathematics Director (JB) External Advisory Board Steering Committee Project Managers Training Board

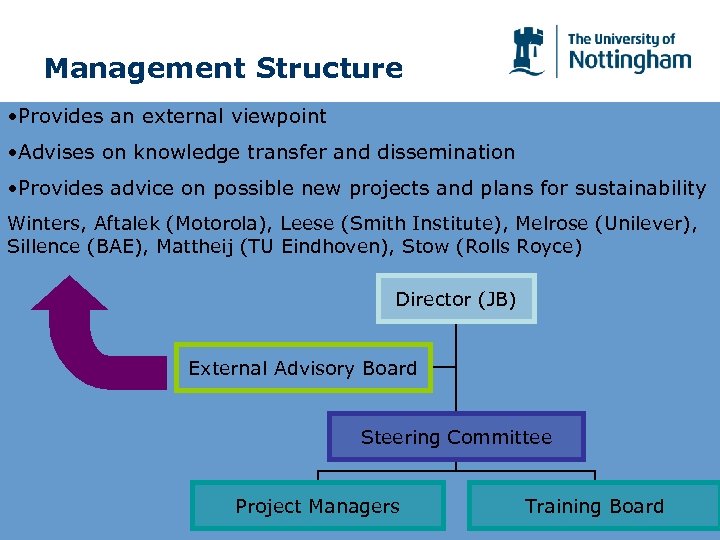Management Structure • Provides an external viewpoint • Advises on knowledge transfer and dissemination • Provides advice on possible new projects and plans for sustainability Winters, Aftalek (Motorola), Leese (Smith Institute), Melrose (Unilever), Sillence (BAE), Mattheij (TU Eindhoven), Stow (Rolls Royce) Director (JB) External Advisory Board Steering Committee Project Managers Training Board

Management Structure • Oversee training programmes for individual Ph. D students and PDRAs • Liaise with industrial partners on placements • Oversee organization of graduate lecture courses and short courses Director (JB) External Advisory Board Steering Committee Project Managers Training Board

Measures of Success By the end of the initial five year funding period: • • New external funding: £ 1 M New projects: 5 New companies involved: 10 Number of different sectors involved : 6 (e. g. communications, defence, pharmaceuticals) • Number of interdisciplinary conferences held: 5 • Number of Visiting Fellows accommodated: 10

The Four Initial Projects Reducing complexity in electromagnetic compatibility problems Industrial Partners BAE Systems

The Four Initial Projects Project Team • Houston, Tew, King (Math. Sciences) • Christopoulos, Sewell (Elec. Eng. ) • PDRA, Ph. D student x 2 Scientific Challenges • Multiscale modelling • Homogenization theory • Numerical methods for EM fields in complex geometries

The Four Initial Projects Statistical shape and image analysis in industrial applications Industrial Partners Audata, Pet. Screen, TSEnse Diagnostics

The Four Initial Projects Project Team • Dryden, Wood (Math. Sciences) • Bai Li (Computer Science) • PDRA, Ph. D student x 2 Scientific Challenges • Statistical analysis of geometrical objects • Shape and image analysis • High-dimension, low sample size (HDLSS) data • Stochastic modelling and Bayesian inference for HDLSS data

The Four Initial Projects Multiphase flow in liquid/liquid separators Industrial Partners Chevron, Shell, Prospect Flow Solutions

The Four Initial Projects Project Team • Cliffe, Hibberd, Riley (Math. Sciences) • Azzopardi (Chem. Eng. ), Yan (Built Env. ) • PDRA, Ph. D student x 2 Scientific Challenges • Lattice-Boltzmann for multiphase flow • Constitutive laws for separation in plate packs

The Four Initial Projects The oxidation of polymeric artificial joint replacements Industrial Partners Perplas

The Four Initial Projects Project Team • Billingham (Math. Sciences) • Everitt (Mech. Eng. ), George (Chemistry) • PDRA, Ph. D student Scientific Challenges • Multiscale and multiphysics modelling • Modelling the chemistry of irradiated UHMWPE • Stochastic homogenization

Mathematical Challenges • The construction of tractable, realistic, models that give insight into real industrial problems • Nonlinear mathematics (homogenization, free boundary problems, gradient flows, …) • Scientific computing and numerical analysis • Modelling with uncertainty in industrial applications

Scientific Computing High Performance Computing Facility • Grid: 1024 Opteron Cluster with 80 TB storage (value £ 3 M) • £ 1 M from SRIF 3 to add to existing cluster Centre for Computational Sciences • Expertise – Computational Applied Mathematics Group (Cliffe, Houston, Hibberd, …) – Significant University strength across a wide spectrum: Engineering, Pharmacy, Physics & Astronomy, Chemistry, Computer Science, … • Training – MSc in Computational Science with: CFD; Continuum Mechanics; Systems Biology; Industrial Mathematics (from 2007)

Statistical Themes • Stochastic homogenization • Locations of cables in multi-wire looms have random variations – global effect? • Small random/deterministic departures from local periodicity -> major global effects • Validation of models from experimental data – statistical inference • Stochastic geometry for amorphous and crystalline grains • Image segmentation and registration

Statistical Themes Statistical shape and image analysis • Stochastic face/signature modelling and recognition [biometrics: security applications] • Proteomic mass-spectrometry and ECG analysis • Fast real-time initial estimates from computational algorithms. Use Bayesian methodology to model uncertainty -> credibility intervals + risk. • Temporal sequences of shape data: moving heads and dynamic signature recognition • Non-Euclidean geometry of shape space • High-dimension, low sample size data analysis is a very challenging and topical area.

The Referees VJTNMX: ‘… a rare … opportunity… to fund a really significant proposal. ’ 35 IUHN: ‘… this situation is light years away from just throwing money at a group and hoping for the best. ’ UJF 949: ‘… a well thought-out proposal… to be encouraged. ’ LR 4 UXH: ‘… well-constructed…cogently argued…deserves to be funded. ’ R 35 QEZ: `… an impressive group of academics. ’ , `… a very strong group of industrial collaborations. ’

Dissemination and Outreach • • At least two Visiting Fellows each year Annual interdisciplinary conferences Annual plenary meeting Liaison with Smith Institute (KTN for Industrial Mathematics) Frequent presentations at conferences Outreach meetings for new and existing industrial partners Web site Journal publications

Key Points • An opportunity to fund timely, high quality interdisciplinary research of relevance to the needs of British industry • Builds on existing strengths to promote the generation of new collaborations and new mathematical insights and methods • Training and dissemination an integral part of the strategy of the Centre • An investment in a Centre that will become selfsustaining over the initial five year period