ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Содержание Центральная симметрия

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Содержание • Центральная симметрия • Построение • Центральная симметрия в окружающем мире • Заключение

Центральная симметрия M A M 1 • Точки М 1 называются симметричными относительно точки А, если A – середина MM 1. • A – центр симметрии

• Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

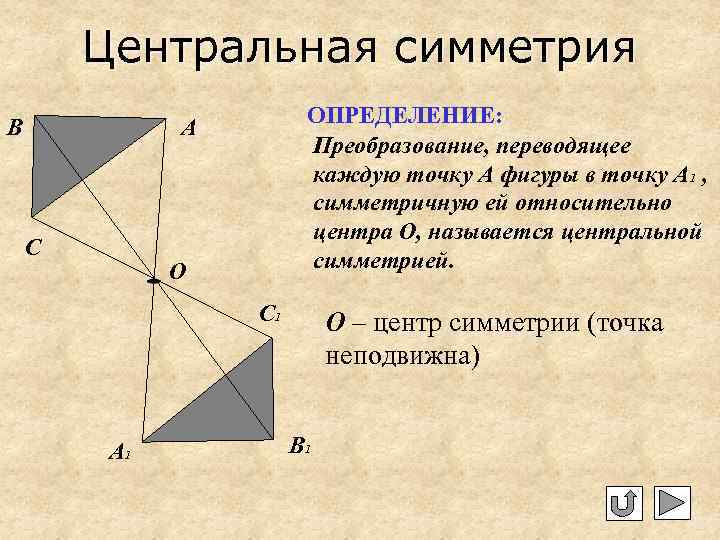Центральная симметрия B ОПРЕДЕЛЕНИЕ: Преобразование, переводящее каждую точку А фигуры в точку А 1 , симметричную ей относительно центра О, называется центральной симметрией. А C О C 1 А 1 О – центр симметрии (точка неподвижна) B 1

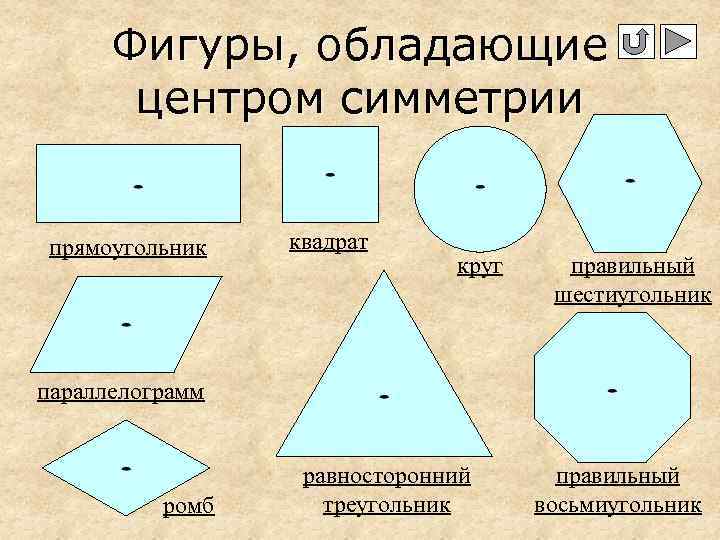Фигуры, обладающие центром симметрии прямоугольник квадрат круг правильный шестиугольник параллелограмм ромб равносторонний треугольник правильный восьмиугольник

Фигуры, не обладающие центральной симметрией Угол Произвольный треугольник Неправильный многоугольник трапеция

Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному

Построение точки, симметричной данной M О 1. ОМ = ОМ 1 2. М 1 – искомая точка M 1 Определение

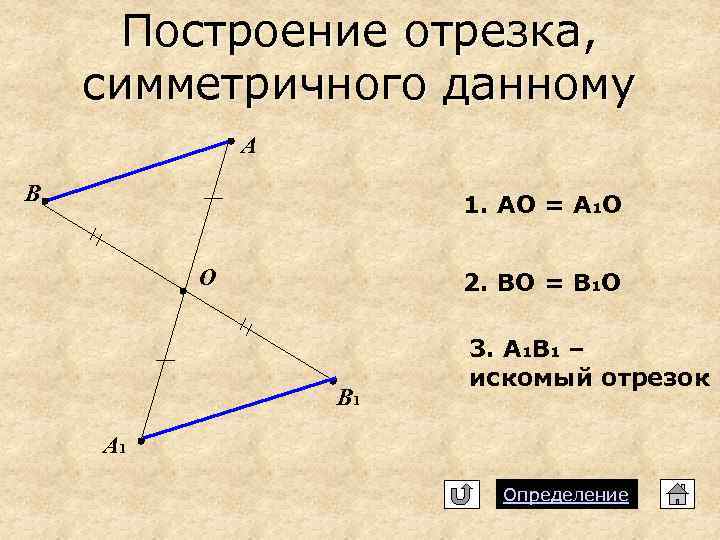Построение отрезка, симметричного данному А B 1. АО = А 1 О О 2. ВО = В 1 О B 1 3. А 1 В 1 – искомый отрезок А 1 Определение

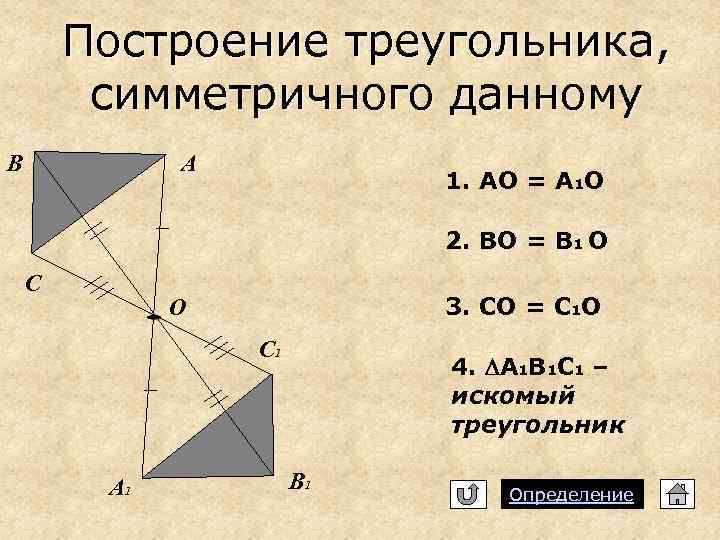Построение треугольника, симметричного данному B А 1. АО = А 1 О 2. ВО = В 1 О C 3. СО = С 1 О О C 1 А 1 4. А 1 В 1 С 1 – искомый треугольник B 1 Определение

Заключение Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство» .