9112b762a0b08aaea476d779d01183b5.ppt
- Количество слайдов: 22

Center for MHD Studies Turbulent MHD flow in a cylindrical vessel excited by a misaligned magnetic field A. Kapusta and B. Mikhailovich Center for MHD Studies Ben-Gurion University of the Negev Beer-Sheva, Israel FLOWCOMAG-2004

Center for MHD Studies It is well-known that there a lot of difficulties in calculations of MHD turbulent rotating flows, and certain approximations are required. In practice, semi-empirical models are frequently used. One of such models is used in our presentation. The matter in point is so called “external” friction approximation described in [1] and modified in [2, 3], where a quasi-linear dissipative term –analog of the divergence of stress tensor- appears. In this case, we can determine azimuthal component of the mean velocity assuming that all turbulent effects including the effect of secondary flows on mean velocity are accounted for through the “external” friction coefficient. FLOWCOMAG-2004

Center for MHD Studies It is defined as where is the mean vorticity of the flow, is an empirical coefficient, - is a parameter defining the flow structure , in the present case, FLOWCOMAG-2004

Center for MHD Studies Note that the “external” friction approximation is based on the results of numerous experimental data and gives reliable results when calculating mean velocities of turbulent rotating MHD flows both under the action of a rotating magnetic field (RMF) and in homeopolar facilities [4]. Moreover, the model has proved to be applicable also to the analysis of the behavior of vortical structures in a turbulent wake behind a bluff body [5]. It is noteworthy that we have managed to obtain a universal dependence of the angular velocity of turbulent flow core on the only dimensionless parameter Q within the frames of this model where FLOWCOMAG-2004

Center for MHD Studies We study the effect of misalignment between the magnetic field rotation axis Z 0 and the symmetry axis of the cylindrical vessel Z on two-dimensional structure of the mean turbulent flow excited by rotating magnetic field (RMF) in non-inductive approximation using the “external” friction model. In practical applications of RMF, for example, in metallurgical processes, the axis of the vessel with melt can be shifted with respect to the inductor axis. Therefore, the characteristics of the mean flow (its structure) can be changed depending both on MHD interaction parameter N and on the eccentricity e. Note that the eccentricity can also change the structure of surface waves on the free surface of a rotating fluid [6]. FLOWCOMAG-2004

Center for MHD Studies If the axes Z 0 and Z coincide, mean radial and azimuthal components of dimensionless electromagnetic body forces are described by the following expressions under the condition (1) where p is the number of pole pairs of the inductor exciting RMF, Fig. 1. Coordinate systems layout FLOWCOMAG-2004

Center for MHD Studies Using the formulas of coordinate and vectorial components transformation at the transition from a certain cylindrical coordinate system to another one we obtain for parallel Z 0 and Z : (2) (3) where (later on we use without upper lines). FLOWCOMAG-2004

Center for MHD Studies Our next step is to estimate z-component of be written as: that can (4) After differentiating (2), (3) and substituting into (4), we obtain: (5) where FLOWCOMAG-2004

Center for MHD Studies In this case a dimensionless equation for z-component of the velocity vector potential can be written as follows (6) which should be solved under the boundary conditions: (7) Neglecting laminar friction in comparison with turbulent one, we seek the solution of (6)-(7) in the form of a sum of even and odd (with respect to j ) solutions: FLOWCOMAG-2004

Center for MHD Studies In the zero approximation, the problem acquires the form: (8) and (9) where It follows from the evenness of F (r, j) function and the operator D with respect to coordinate j that is also even, and the problem (8)-(9) is solved in the form: (10) where are the roots of the equations for Bessel functions: FLOWCOMAG-2004

Center for MHD Studies Substituting (10) into (8) and performing the procedure of Galerkin’s method, we obtain: (11) (12) where FLOWCOMAG-2004

Center for MHD Studies In the first approximation, the problem can be written as: (13) and It follows from the oddness of the F*(r, j) function with respect to coordinate j that the problem (13) can be solved in the form: (14) FLOWCOMAG-2004

Center for MHD Studies Substituting (14) into (13) and performing the procedure of Galerkin’s method, and taking into account the fact that we obtain (15) where FLOWCOMAG-2004

Center for MHD Studies We have found exact solutions in the cases of p=1 and p=2. At p=1: (16) At p=2: (17) FLOWCOMAG-2004
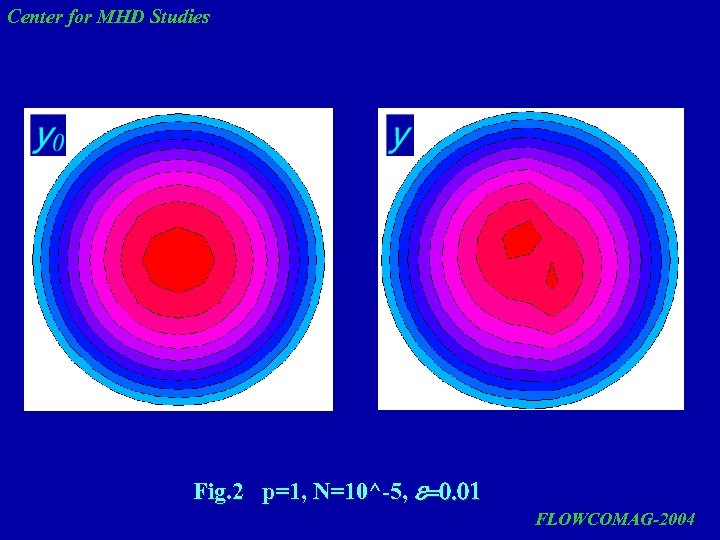
Center for MHD Studies Fig. 2 p=1, N=10^-5, e=0. 01 FLOWCOMAG-2004
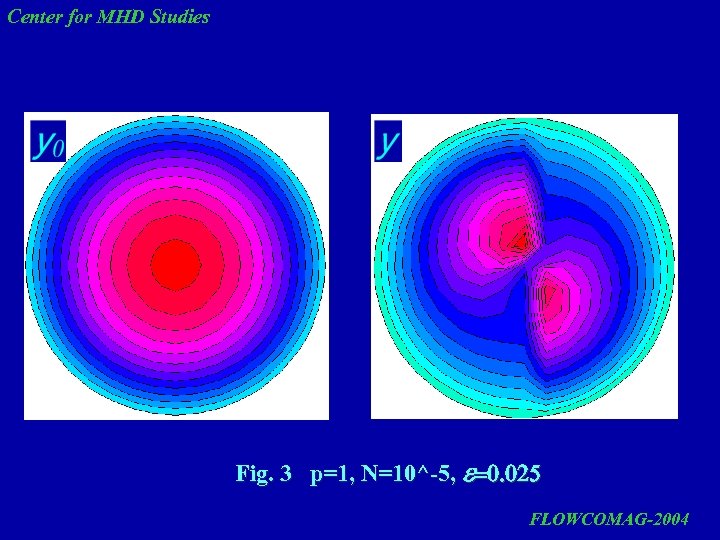
Center for MHD Studies Fig. 3 p=1, N=10^-5, e=0. 025 FLOWCOMAG-2004
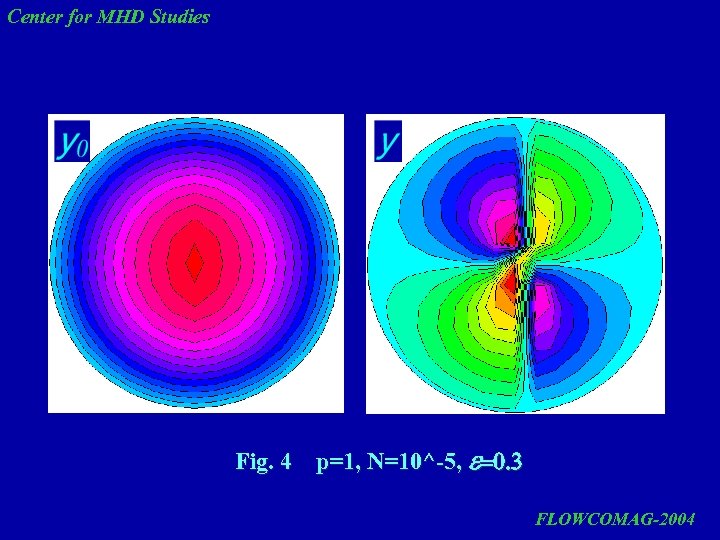
Center for MHD Studies Fig. 4 p=1, N=10^-5, e=0. 3 FLOWCOMAG-2004
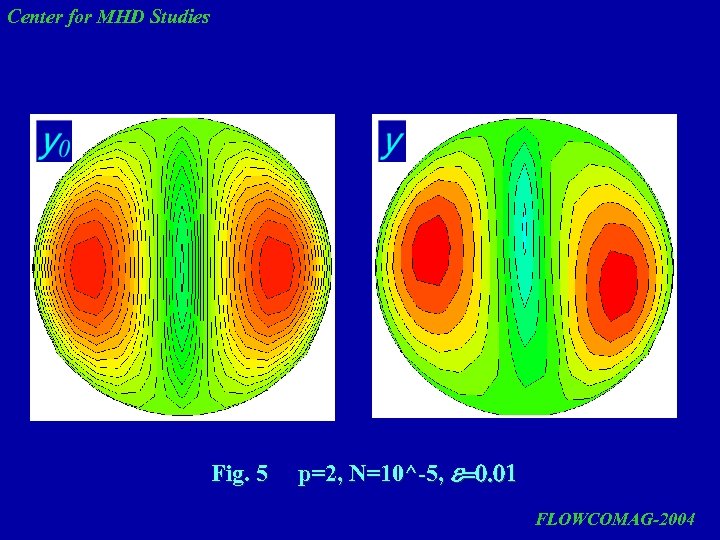
Center for MHD Studies Fig. 5 p=2, N=10^-5, e=0. 01 FLOWCOMAG-2004
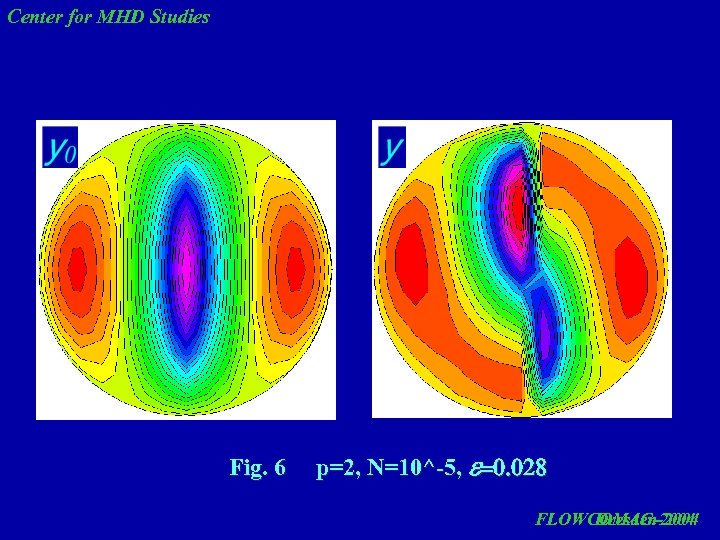
Center for MHD Studies Fig. 6 p=2, N=10^-5, e=0. 028 FLOWCOMAG-2004 Dresden-2004
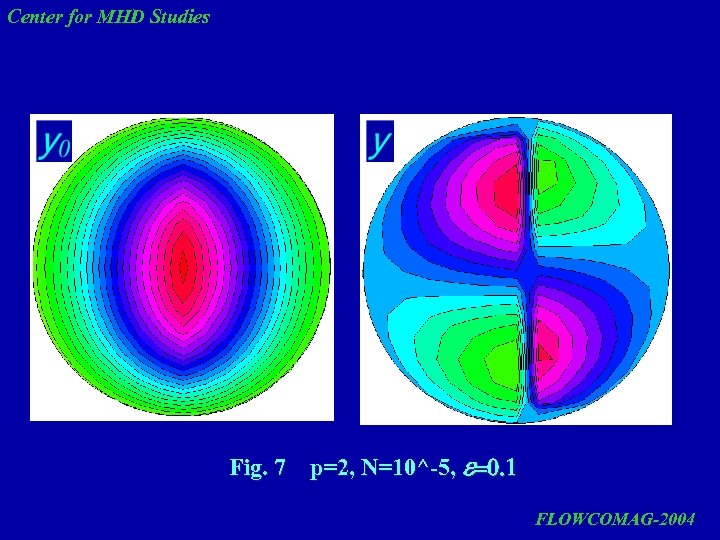
Center for MHD Studies Fig. 7 p=2, N=10^-5, e=0. 1 FLOWCOMAG-2004

Center for MHD Studies The results of flow streamlines calculations show that linear approximation (first term of solution) gives a rotating flow, which gets deformed in the core at increasing eccentricity. The account for nonlinearity changes the flow pattern. In this case, all effects occur in the core on the background of mean rotating flow. It is desirable to perform experimental checking of the computed results, since the appearance of such structures may be useful for technological applications as a possible means of controlling liquid metal behavior under a rotating magnetic field. FLOWCOMAG-2004

Center for MHD Studies References 1. Kapusta, A. B. , Levitsky, L. D. , On the universalization of the model of turbulent magnetohydrodynamic rotation, Magnitnaya Gidrodinamika, 3 (1991 a) 134 -136. 2. Kapusta, A. B. , Shamota, V. P. , Quasi-laminar and turbulent flows of a conductive fluid, Magnetohydrodynamics, 32 (1996) 43 -49. 3. A. Kapusta, B. Mikhailovich, Golbraikh, E. 2002. Semiempirical model of turbulent rotating MHD flows. Proc. 5 th Internat. PAMIR Conf, I-227230. 4. Branover et al. 2002. Turbulent MHD rotation of a conducting fluid in a cylindrical vessel. Proc. 5 th Internat. PAMIR Conf. , 2002, I-169 -171. 5. Kapusta, A. , B. Mikhailovich, E. Golbraikh, 2000. On the development of a turbulent vortex in an axial magnetic field, Proc. 4 th International Conference on Magnetohydrodynamics PAMIR, 627 -630. 6. Golbraikh, E. , Kapusta, A. and Mikhailovich, B. 2002. Standing waves on the surface of a conducting fluid rotating in a magnetic field. Proc. 9 th European Turbulence Conf. , 2002, 885. FLOWCOMAG-2004
9112b762a0b08aaea476d779d01183b5.ppt