ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ Презентацию составили Лапина

ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ. Презентацию составили: Лапина Мария Баженова Мария Лебедева Анастасия

ОПРЕДЕЛЕНИЕ УРАВНЕНИЯ ЦЕЛЫМ УРАВНЕНИЕМ С ОДНОЙ ПЕРЕМЕННОЙ НАЗЫВАЕТСЯ УРАВНЕНИЕ, ЛЕВАЯ И ПРАВАЯ ЧАСТИ КОТОРОГО – ЦЕЛЫЕ ВЫРАЖЕНИЯ. Примеры целых уравнений: 0, 7 x 7 -3 x 5 -x=5 Любое уравнение можно преобразовать в равносильное ему уравнение вида P(x)=0 Известно что алгебраическая сумма и произведение многочленов, есть многочлен, поэтому с помощью тождественных преобразований каждое целое рациональное выведении можно представить в виде многочлена.

СТЕПЕНЬ УРАВНЕНИЯ. Степенью уравнение вида P(x)=0, где P(x)многочлен стандартного вида, называется степень этого многочлена. Степенью произвольного целого уравнения называется степень равносильного ему уравнения указанного вида.

ТЕОРЕМА. ЕСЛИ УРАВНЕНИЕ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ ИМЕЕТ ЦЕЛЫЙ КОРЕНЬ, ТО МОЖНО ИСПОЛЬЗОВАТЬ СЛЕДУЮЩУЮ ТЕОРЕМУ. Т. Если уравнение A 0 xn+A 1 xn-1+…+An-1 x+An=0, в котором все коэффициенты целые числа, при чем свободный член отличный от нуля, имеет целый корень, то этот корень является делителем свободного члена.

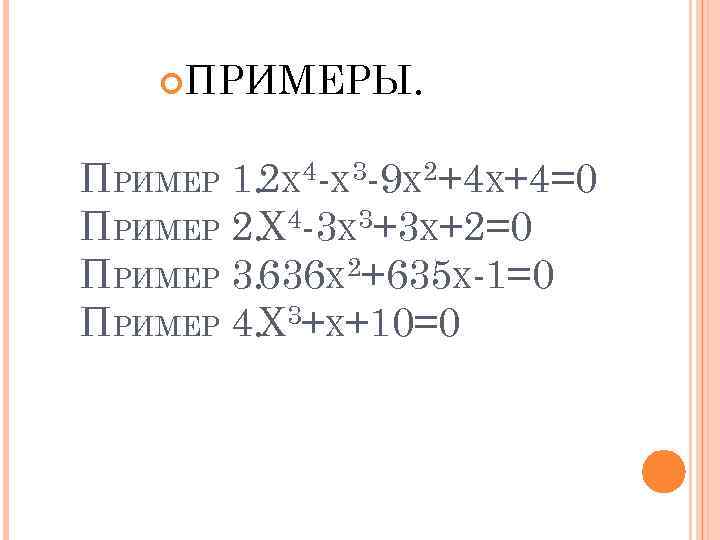ПРИМЕРЫ. ПРИМЕР 1. 2 X 4 -X 3 -9 X 2+4 X+4=0 ПРИМЕР 2. X 4 -3 X 3+3 X+2=0 ПРИМЕР 3. 636 X 2+635 X-1=0 ПРИМЕР 4. X 3+X+10=0

КАК РЕШАТЬ ТАКИЕ ПРИМЕРЫ? Делителями свободного члена явлются числа 1, -1, 2, -2, 4, -4. Подставляя эти числа в уравнения, найдем, что его левая часть обращается в нуль, при x, равном 1, -2, 2. Значит, уравнение имеет три целых корня X 1=1 X 2=-2 X 3=2. Ответ: 1, -2, 2.

Для уравнений пятой степени и более высоких степеней, как доказал в 20 -х годах 19 века норвежский математик Н. Абель (1802 -1829), формул вообще не существует.