Целочисленное программирование Целочисленным или дискретным

Целочисленное программирование

• Целочисленным (или дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна. • Методы целочисленной оптимизации можно разделить на три основные группы: а) методы отсечения; б) комбинированные методы; в) приближенные методы. • Рассмотрим один из методов отсечения — метод Гомори. Сущность методов отсечения состоит в том, что сначала задача решается без учета условия целочисленности. Если полученный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: а) оно должно быть линейным; б) должно отсекать найденный оптимальный нецелочисленный план; в) не должно отсекать ни одного целочисленного плана.

Дополнительное ограничение, обладающее этими свойствами, называется правильным отсечением. Задача целочисленного линейного программирования формулируется также, как и задача линейного программирования. Разница состоит в том, что на переменные в оптимальном решении накладывается дополнительное требование их целочисленности. Это обусловлено тем, что в ряде задач (например, при определении оптимального плана выпуска машин, агрегатов, размещения оборудования, предприятий и т. п. ) переменные характеризуют физически неделимые единицы, и поэтому должны принимать только целые значения.

В общем случае задача целочисленного линейного программирования формулируется следующим образом: найти максимум или минимум функции при ограничениях Если r=n, то задача будет полностью целочисленной; если r < n, то - частично целочисленной.

Решение полностью целочисленной задачи методом Гомори Этот метод основан на симплекс-методе. Симплексным методом находится оптимальное решение задачи без учета целочисленности переменных Если оптимальное решение оказывается целочисленным, то решение задачи заканчивается. Если полученное оптимальное решение нецелочисленное, то из последней системы ограничений выбирается уравнение, для которого дробная часть координаты оптимального решения имеет наибольшее значение. На его основе составляется дополнительное ограничение. Дополнительное ограничение отсекает от области допустимых решений нецелочисленное оптимальное решение, но при этом сохраняет целочисленные вершины этой области.

Пусть получено оптимальное решение задачи целочисленного линейного программирования симплекс-методом, и в этом решении переменная x k нецелое число. Выпишем соответствующее ограничение задачи, находящееся в последней симплексной таблице: где xk - базисная переменная в уравнении; h k j – коэффициенты при неизвестных (коэффициенты разложений векторов условий по базису опорного решения); x j – свободные переменные в системе уравнений; f k – правая часть уравнения (координата оптимального решения), которая является дробным числом.

Разобьем каждый коэффициент и свободный член этого уравнения на два слагаемых: целую и дробную части. Целая часть числа а – это наиболее близкое к этому числу целое число, не превосходящее самого числа. Обозначим целую часть числа так [a]. Дробная часть числа а находится как разность этого числа и его целой части. Дробная часть числа всегда неотрицательна и меньше единицы. Дробную часть числа будем обозначать {a}. Тогда:

Для числа Например : • целая часть =2 • дробная часть равна Для числа : • целая часть • дробная часть равна

Уравнение (1) запишем в следующем виде: На его основе имеем дополнительное ограничение: следующее

Заменяя это неравенство уравнением и добавляя его к ранее решенной задаче, получаем новую задачу. Решаем ее симплекс-методом. Если новое оптимальное решение не будет целочисленным, то по последней симплексной таблице составляем новое дополнительное ограничение. Если в оптимальном плане несколько дробных x k, то дополнительное ограничение составляется для max {x k }. Процесс присоединения дополнительных ограничений повторяют до тех пор, пока не будет найден целочисленный опорный оптимальный план или не будет доказано, что задача не имеет целочисленных планов. Это имеет место в том случае, когда для дробного x k все коэффициенты при других неизвестных в этой строке окажутся целыми.

Пример при ограничениях: xi ≥ 0, xi – целые, i=1, 2, 3, 4, 5.

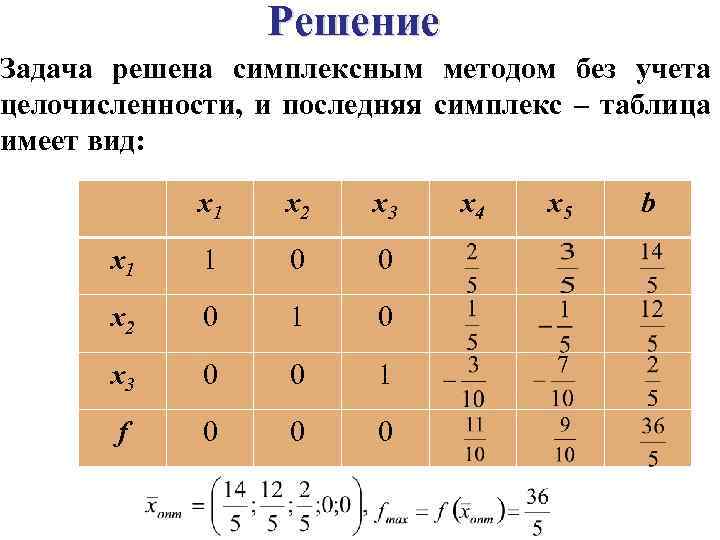Решение Задача решена симплексным методом без учета целочисленности, и последняя симплекс – таблица имеет вид: . x 1 x 2 x 3 x 1 1 0 0 x 2 0 1 0 x 3 0 0 1 f 0 0 0 x 4 x 5 b

Полученное оптимальное решение -нецелочисленное: - нецелые числа. Выберем из них число с наибольшей дробной частью: Итак, выбираем правую часть, соответствующую переменной x 1. Из таблицы выписываем строку, содержащую переменную x 1:

Следовательно, дополнительное ограничение имеет вид или (при замене его уравнением) где x 6 – балансовая переменная, x 6 ≥ 0. Присоединив это ограничение к исходной задаче, получаем новую задачу. Для ее решения в последнюю симплекс – таблицу исходной задачи добавляем строку, соответствующую введенному ограничению.

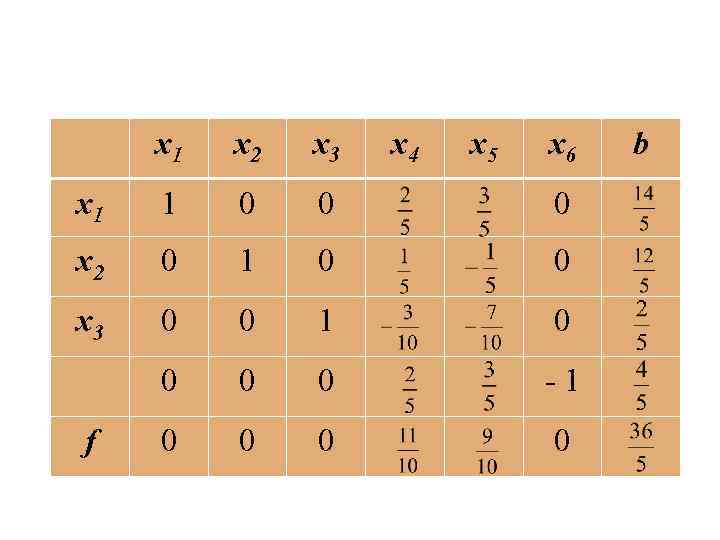x 1 x 2 x 3 x 1 1 0 0 0 x 2 0 1 0 0 x 3 0 0 1 0 0 -1 0 0 f x 4 x 5 x 6 b

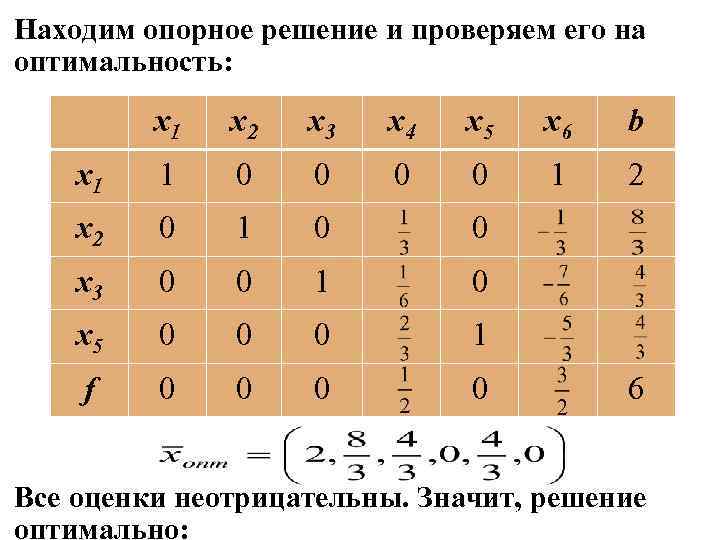Находим опорное решение и проверяем его на оптимальность: x 1 x 2 x 3 x 4 x 5 x 6 b x 1 1 0 0 1 2 x 2 0 1 0 0 x 3 0 0 1 0 x 5 0 0 0 1 f 0 0 6 Все оценки неотрицательны. Значит, решение оптимально:

Однако нарушается условие целочисленности. Поэтому требуется составить еще одно дополнительное ограничение на основе последней симплексной таблицы. Выписываем из нее вторую строку: Дополнительное ограничение имеет вид: или

Добавив в последнюю симплекс-таблицу дополнительное ограничение, получим новую задачу: x 1 x 2 x 3 x 4 x 5 x 6 x 7 b x 1 x 2 x 3 x 5 f 1 0 0 0 1 0 0 0 0 -1 0 2 6

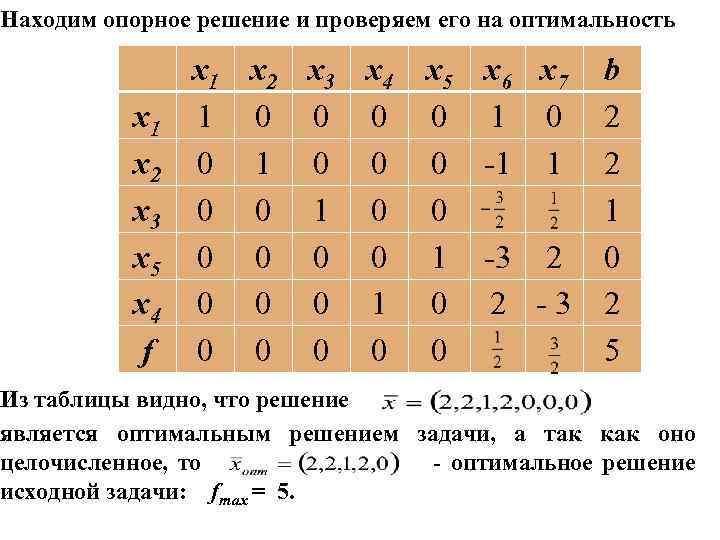Находим опорное решение и проверяем его на оптимальность x 1 x 2 x 3 x 5 x 4 f x 1 x 2 x 3 x 4 x 5 x 6 x 7 1 0 0 0 -1 1 0 0 0 0 1 -3 2 0 0 0 1 0 2 -3 0 0 0 b 2 2 1 0 2 5 Из таблицы видно, что решение является оптимальным решением задачи, а так как оно целочисленное, то - оптимальное решение исходной задачи: fmax = 5.