Цель урока Показать как используется скалярное произведение векторов

Цель урока: Показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, между прямой и плоскостью.

П. 52, • № 464(б, в, г), № 466 (б), • № 471, № 467 (б) – двумя способами • Готовиться к зачету

Повторяем теорию: • Как находят координаты вектора, если известны координаты его начала и конца? • Как находят координаты середины отрезка? • Как находят длину вектора? • Как находят расстояние между точками?

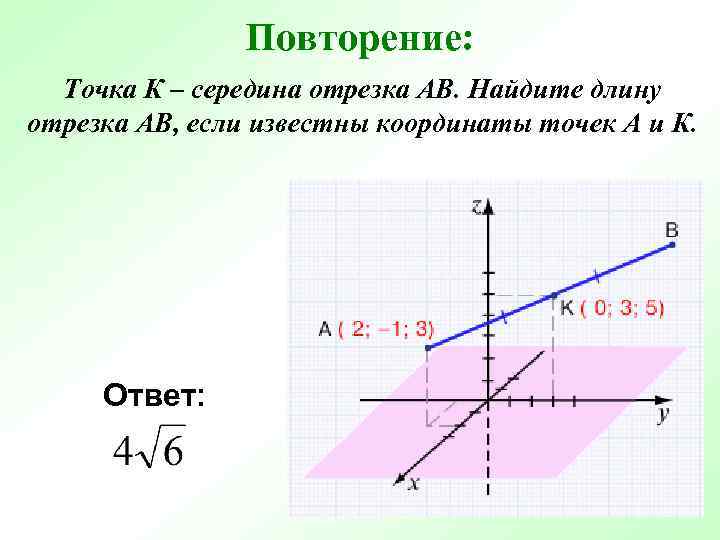Повторение: Точка К – середина отрезка АВ. Найдите длину отрезка АВ, если известны координаты точек А и К. Ответ:

Повторение: Дан куб АВСDA 1 B 1 C 1 D 1. Найдите угол между векторами: а) и б) и B 1 450 A 1 C 1 D 1 450 B в) и 1350 A C D

Повторяем теорию: • Какие векторы называются перпендикулярными? • Что называется скалярным произведением векторов? • Чему равно скалярное произведение перпендикулярных векторов? • Чему равен скалярный квадрат вектора? 0 • При каком условии скалярное произведение ненулевых векторов положительно ? отрицательно? равно 0?

11 класс.

ал ери ат йм овы Н

Направляющий вектор прямой а В А Определение: Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо на прямой, параллельной ей.

№ 1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых. а) б) θ θ φ=θ φ = 1800 - θ

I. Угол между двумя прямыми Если , направляющие векторы прямых a и b, то a b=

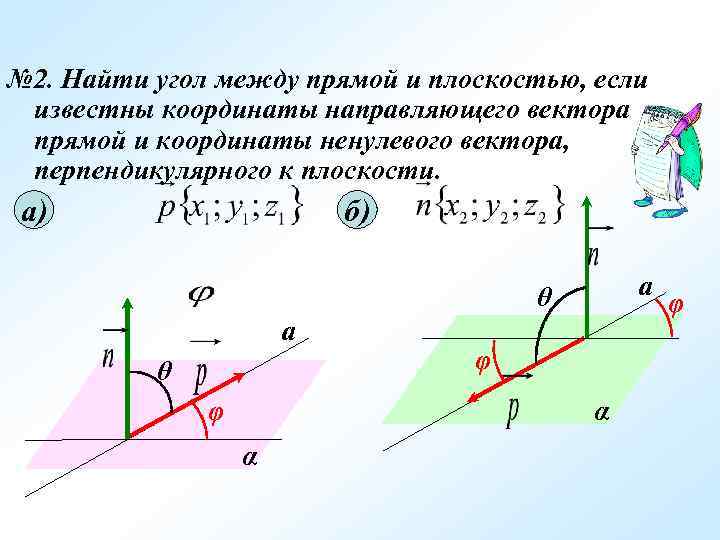№ 2. Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости. а) б) а θ φ φ α α φ

II. Угол между прямой и плоскостью Если прямой a, - направляющий вектор - вектор, перпендикулярный к плоскости, то

№ 464 (а) Дано: Найти: угол между прямыми АВ и CD. Ваши предложения… 1. Найдем координаты векторов и 2. Воспользуемся формулой: φ = 300

№ 466 (а) Дано: куб АВСDA 1 B 1 C 1 D 1 точка М принадлежит АА 1 АМ : МА 1 = 3 : 1; N – середина ВС Вычислить косинус угла между прям. MN и DD 1 z 1. Введем систему координат. D 1 2. Рассмотрим DD 1 и МN. A 1 3. Пусть АА 1= 4, тогда 4. Найдем координаты векторов DD 1 и MN. 5. По формуле найдем cosφ. Ответ: C 1 B 1 М D A у C B N х

Задача. Дано: прямоугольный параллелепипед АВСDA 1 B 1 C 1 D 1; DA = 2; DC = 2; DD 1 = 3. Найти: СВ 1 , D 1 B Решение: 1. Введем систему координат Dxyz 2. Рассмотрим направляющие A 1 прямых D 1 B и CB 1. z D 1 C 1 B 1 3 3. По формуле найдем cosφ. D arccos …. 2 х A 2 C B у

№ 467 (а) Дано: прямоугольный параллелепипед АВСDA 1 B 1 C 1 D 1; АВ = ВС = ½ АА 1 Найти: 1 способ: ВD , CD 1 1. Введем систему координат Bxyz 2. Пусть АА 1= 2, тогда A 1 АВ = ВС = 1. z C 1 B 1 3. Координаты векторов: х D 4. Находим косинус угла между прямыми: у A C B

№ 467 (а) Дано: прямоугольный параллелепипед АВСDA 1 B 1 C 1 D 1; АВ = ВС = ½ АА 1 Найти угол между прямыми ВD и CD 1. 2 способ: D 1 1. Т. к. СD 1|| ВА 1, то углы между ВD и ВА 1; ВD и СD 1 – A 1 равны. 2. В ΔВDА 1: ВА 1 = √ 5, А 1 D = √ 5 z C 1 B 1 3. ΔВDА: по теореме Пифагора х D 4. По теореме косинусов: у A C B

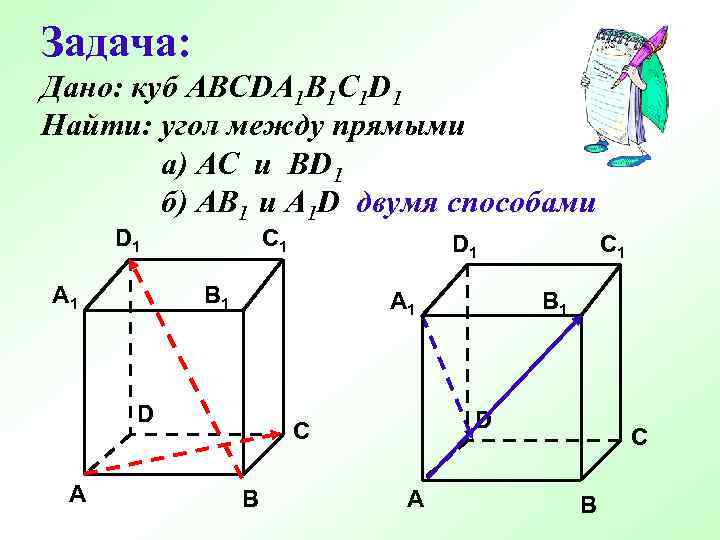Задача: Дано: куб АВСDA 1 B 1 C 1 D 1 Найти: угол между прямыми а) АС и BD 1 б) AB 1 и A 1 D двумя способами D 1 A 1 C 1 В 1 A 1 D A D 1 В 1 D C B C 1 A C B

Что скажут о тебе другие, если ты сам о себе ничего сказать не можешь. Кузьма Прутков Самостоятельная работа Удачи!!!

№ 450 Дано: A(0; 1; -2), В( ; 1; 2), С( ; 2; 1), Д(0; 2; 1) Докажите: АВСД – квадрат План: 1) 2) 3) АВСД – параллелограмм АВСД – ромб АВСД – квадрат