CE 1205 CONSTRUCTION MATERIALS WEEK 3 Chapter 2

CE 1205 CONSTRUCTION MATERIALS WEEK 3 Chapter 2 (Part 2/2) Mechanical Properties of Metals Power. Point® Slides by Salmaliza Salleh Last Updated: © LMS SEGi education group 1

Learning Objectives • Last Updated: To teach the students to draw and interpret stress-strain diagram. © LMS SEGi education group 2

Learning Outcomes • Last Updated: At the end of the class, students must be able to draw and interpret stress-strain diagram. © LMS SEGi education group 3

Concepts of Stress and Strain (tension and compression) • To compare specimens of different sizes, the load is calculated per unit area. Engineering stress: σ = F / Ao • • Last Updated: F is load applied perpendicular to specimen cross section; Ao is cross-sectional area (perpendicular to the force) before application of the load. © LMS SEGi education group 4

Engineering strain: ε = Δl / lo (× 100 %) • Last Updated: Δl is change in length, lo is the original length. Stress and strain are positive for tensile loads, negative for compressive loads © LMS SEGi education group 5

Concepts of Stress and Strain (shear and torsion) Shear stress: τ = F / Ao • F is load applied parallel to the upper and lower faces each of which has an area Ao. Shear strain: γ = tanθ (× 100 %) • Last Updated: θ is strain angle © LMS SEGi education group 6

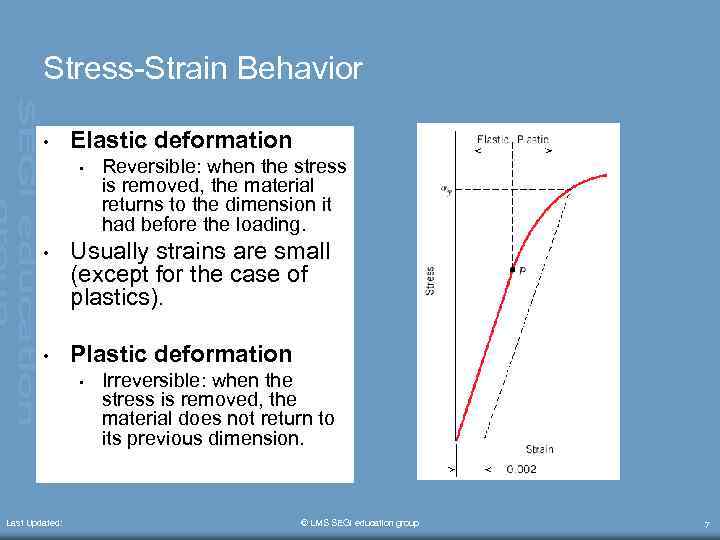Stress-Strain Behavior • Elastic deformation • Reversible: when the stress is removed, the material returns to the dimension it had before the loading. • Usually strains are small (except for the case of plastics). • Plastic deformation • Last Updated: Irreversible: when the stress is removed, the material does not return to its previous dimension. © LMS SEGi education group 7

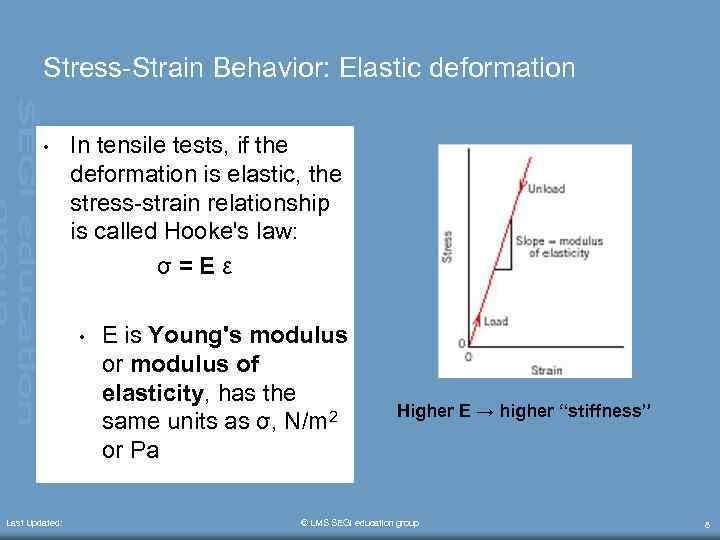Stress-Strain Behavior: Elastic deformation • In tensile tests, if the deformation is elastic, the stress-strain relationship is called Hooke's law: σ=Eε • Last Updated: E is Young's modulus or modulus of elasticity, has the same units as σ, N/m 2 or Pa Higher E → higher “stiffness” © LMS SEGi education group 8

Elastic Deformation: Poisson’s ratio • • • Last Updated: Materials subject to tension, shrink laterally. Those subject to compression, bulge. The ratio of lateral (transverse) and axial strains is called the Poisson's ratio υ. UNLOADED © LMS SEGi education group LOADED 9

Elastic Deformation: Poisson’s ratio • Assuming that the material is compressed along the axial direction: where • • • Last Updated: ν is the resulting Poisson's ratio, is transverse strain (negative for axial tension, positive for axial compression) is axial strain (positive for axial tension, negative for axial compression). Rectangular specimen subject to compression © LMS SEGi education group 10

υ is dimensionless, sign shows that lateral strain is in opposite sense to longitudinal strain Theoretical value for isotropic material: 0. 25 Maximum value: 0. 50, Typical value: 0. 24 0. 30 • • • *"isotropic" means having identical values of a property; uniformity in all directions Last Updated: © LMS SEGi education group 11

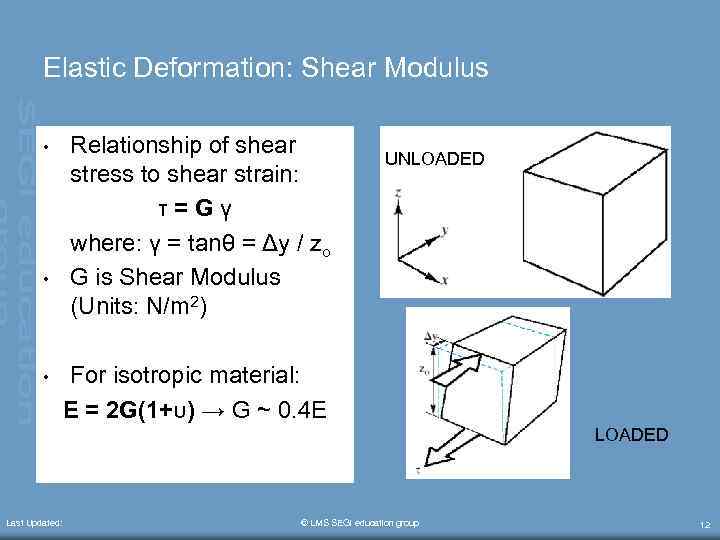Elastic Deformation: Shear Modulus • • • Relationship of shear stress to shear strain: τ=Gγ where: γ = tanθ = Δy / zo G is Shear Modulus (Units: N/m 2) UNLOADED For isotropic material: E = 2 G(1+υ) → G ~ 0. 4 E LOADED Last Updated: © LMS SEGi education group 12

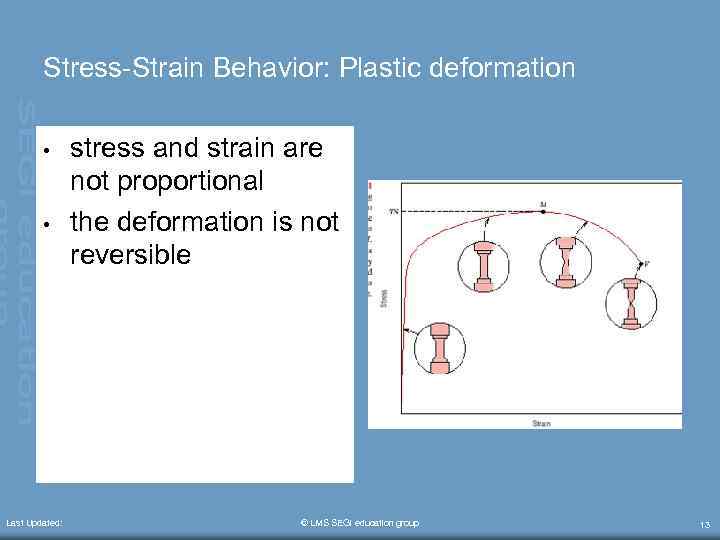Stress-Strain Behavior: Plastic deformation • • Last Updated: stress and strain are not proportional the deformation is not reversible © LMS SEGi education group 13

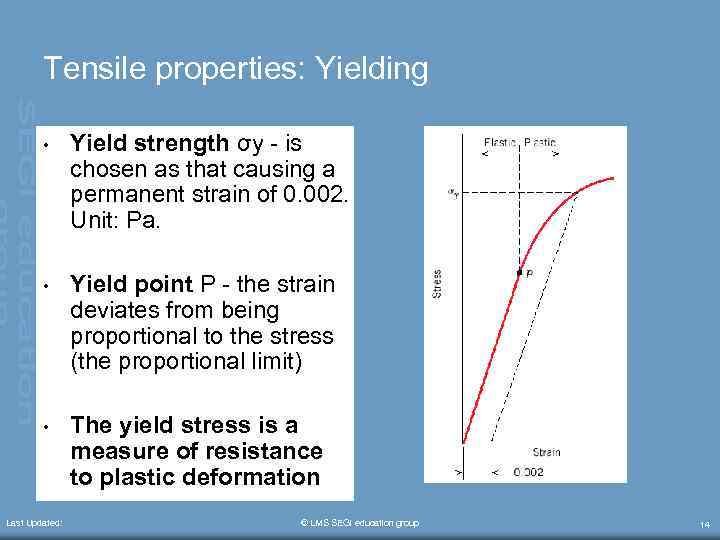Tensile properties: Yielding • Yield strength σy - is chosen as that causing a permanent strain of 0. 002. Unit: Pa. • Yield point P - the strain deviates from being proportional to the stress (the proportional limit) • The yield stress is a measure of resistance to plastic deformation Last Updated: © LMS SEGi education group 14

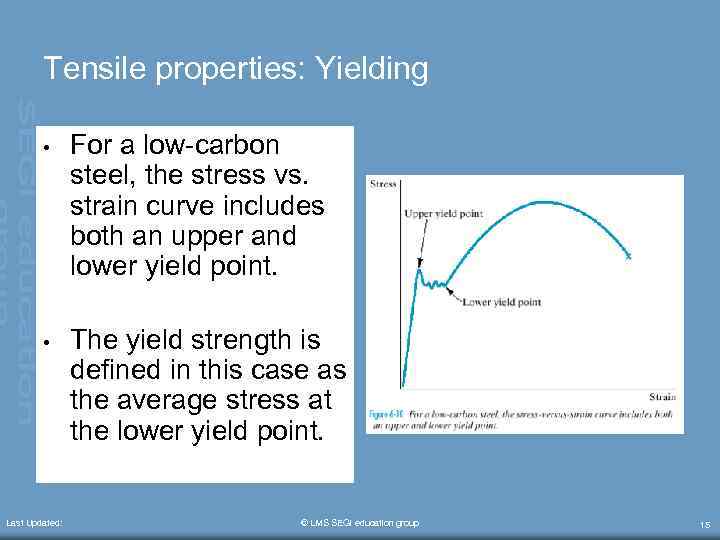Tensile properties: Yielding • For a low-carbon steel, the stress vs. strain curve includes both an upper and lower yield point. • The yield strength is defined in this case as the average stress at the lower yield point. Last Updated: © LMS SEGi education group 15

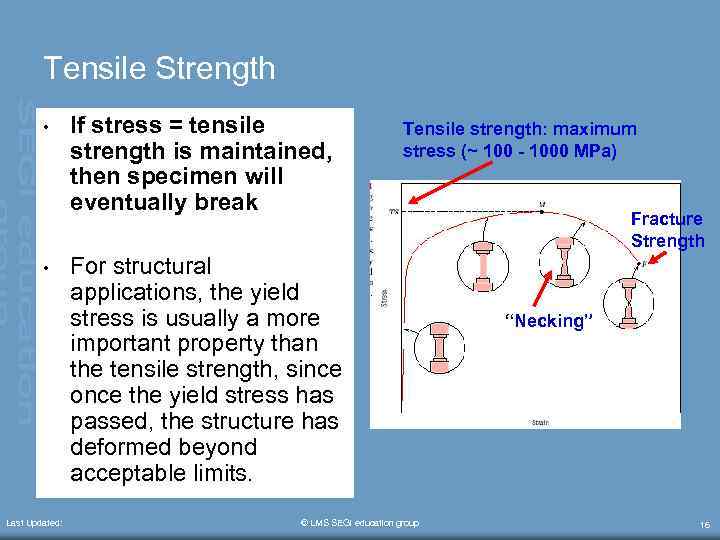Tensile Strength • • Last Updated: If stress = tensile strength is maintained, then specimen will eventually break Tensile strength: maximum stress (~ 100 - 1000 MPa) For structural applications, the yield stress is usually a more important property than the tensile strength, since once the yield stress has passed, the structure has deformed beyond acceptable limits. © LMS SEGi education group Fracture Strength “Necking” 16

Stress-Strain Relationships in Metals • • If a piece of mild structural steel is subjected to an increase of tensile load, it will begin to elongate constantly within certain limit. Then, the elongation will still increase without the increase in stress. • Elastic limit: the largest stress which a material can withstand without being permanently deformed. • Yield point, fy: at which the curve exhibits increase in strain without an increase in stress. • Last Updated: The shape of diagram varies with different loading, type of metal & temperature. Modulus of elasticity, E: is the slope of the stressstrain curve. © LMS SEGi education group 17

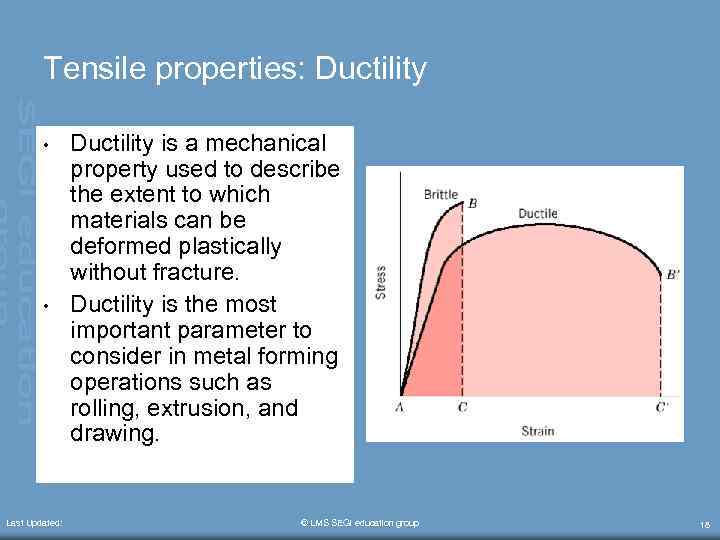Tensile properties: Ductility • • Last Updated: Ductility is a mechanical property used to describe the extent to which materials can be deformed plastically without fracture. Ductility is the most important parameter to consider in metal forming operations such as rolling, extrusion, and drawing. © LMS SEGi education group 18

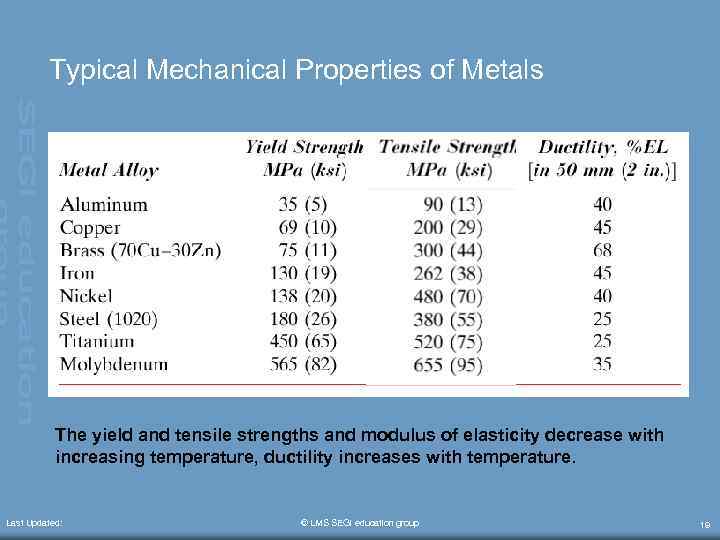Typical Mechanical Properties of Metals The yield and tensile strengths and modulus of elasticity decrease with increasing temperature, ductility increases with temperature. Last Updated: © LMS SEGi education group 19

Hardness • • • Last Updated: Hardness is a measure of the material’s resistance to localized plastic deformation e. g. dent or scratch A qualitative Moh’s scale, determined by the ability of a material to scratch another material: from 1 (softest = talc) to 10 (hardest = diamond). © LMS SEGi education group DENT SCRATCH 20

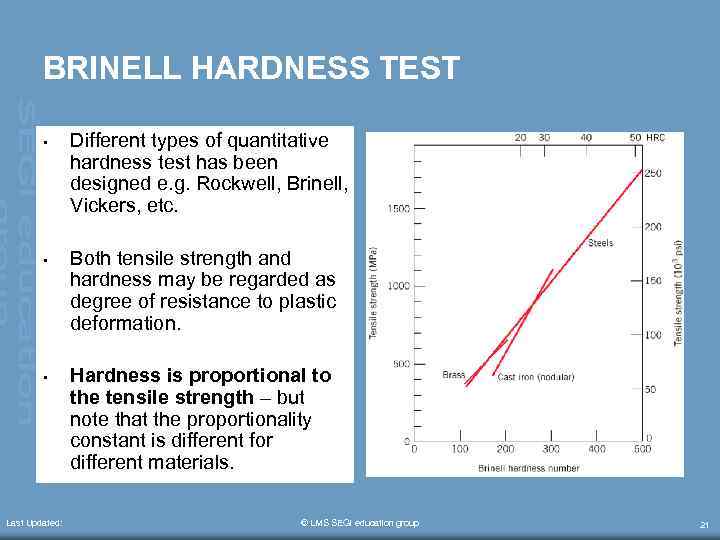BRINELL HARDNESS TEST • Different types of quantitative hardness test has been designed e. g. Rockwell, Brinell, Vickers, etc. • Both tensile strength and hardness may be regarded as degree of resistance to plastic deformation. • Hardness is proportional to the tensile strength – but note that the proportionality constant is different for different materials. Last Updated: © LMS SEGi education group 21

REFERENCES • http: //www. materialsengineer. com/CAcorrosion. htm • http: //www. tis-gdv. de/tis_e/misc/korro. htm • http: //www. engineeringtoolbox. com/corrosiond_986. html • http: //www. tech. plym. ac. uk/sme/mats 340/cpintro. pdf Last Updated: © LMS SEGi education group 22

ANY QUESTIONS? Last Updated: © LMS SEGi education group 23