CDO correlation smile and deltas under different correlations

CDO correlation smile and deltas under different correlations Jens Lund 1 November 2004

Outline l Standard CDO’s l Gaussian copula model l Implied correlation l Correlation smile in the market l Compound correlation base correlation l Delta hedge amounts l New copulas with a smile l Are deltas consistent? 2 1 November 2004 CDO correlation smile and deltas under different correlations

Standardized CDO tranches 100% l l i. Traxx Europe – 125 liquid names – Underlying index CDSes for sectors – 5 standard tranches, 5 Y & 10 Y – First to default baskets – US index CDX Has done a lot to provide liquidity 88% Super senior 22% Mezzanine in structured credit l Reliable pricing information available Implied correlation information 3 1 November 2004 CDO correlation smile and deltas under different correlations 3% equity 12% 9% 6% 3%

Reference Gaussian copula model l N credit names, i = 1, …, N l Default times: l curves bootstrapped from CDS quotes l Ti correlated through the copula: ~ Fi(Ti) = (Xi) with X = (X 1, …, XN)t ~ N(0, ) correlation matrix, variance 1, constant correlation l 4 In model: correlation independent of product to be priced 1 November 2004 CDO correlation smile and deltas under different correlations

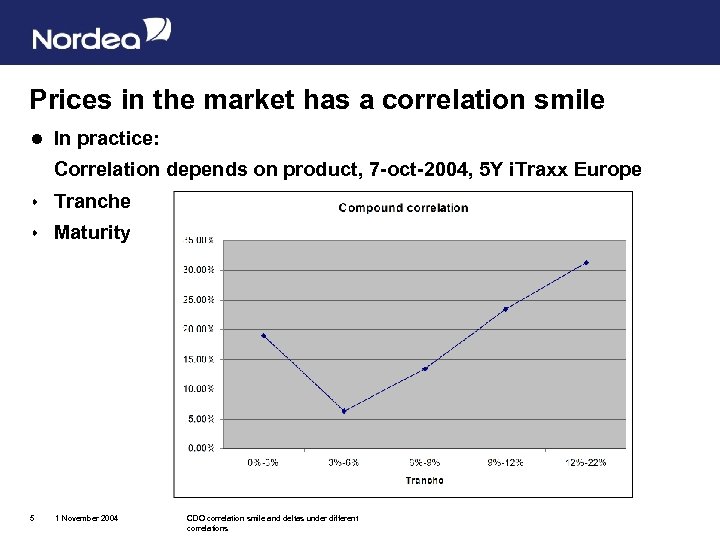Prices in the market has a correlation smile l In practice: Correlation depends on product, 7 -oct-2004, 5 Y i. Traxx Europe s Tranche s Maturity 5 1 November 2004 CDO correlation smile and deltas under different correlations

Why do we see the smile? l Spreads not consistent with basic Gaussian copula l Different investors in different tranches have different preferences l If we believe in the Gaussian model: Market imperfections are present and we can arbitrage! – However, we are more inclined to another conclusion: l Underlying/implied distribution is not a Gaussian copula l We will not go further into why we see a smile, but rather look at how to model it. . . 6 1 November 2004 CDO correlation smile and deltas under different correlations

Compound correlations l The correlation on the individual tranches l Mezzanine tranches have low correlation sensitivity and even non-unique correlation for given spreads l No way to extend to, say, 2%-5% tranche or bespoke tranches l 7 What alternatives exists? 1 November 2004 CDO correlation smile and deltas under different correlations

Base correlations l Started in spring 2004 l Quote correlation on all 0%-x% tranches l Prices are monotone in correlation, i. e. uniqueness l 2%-5% tranche calculated as: – Long 0%-5% – Short 0%-2% l Can go back and forth between base and compound correlation l Still no extension to bespoke tranches 8 1 November 2004 CDO correlation smile and deltas under different correlations

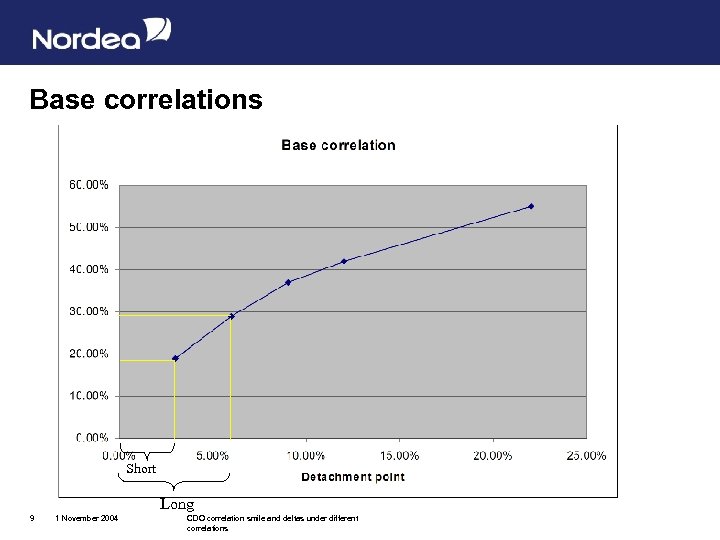Base correlations Short Long 9 1 November 2004 CDO correlation smile and deltas under different correlations

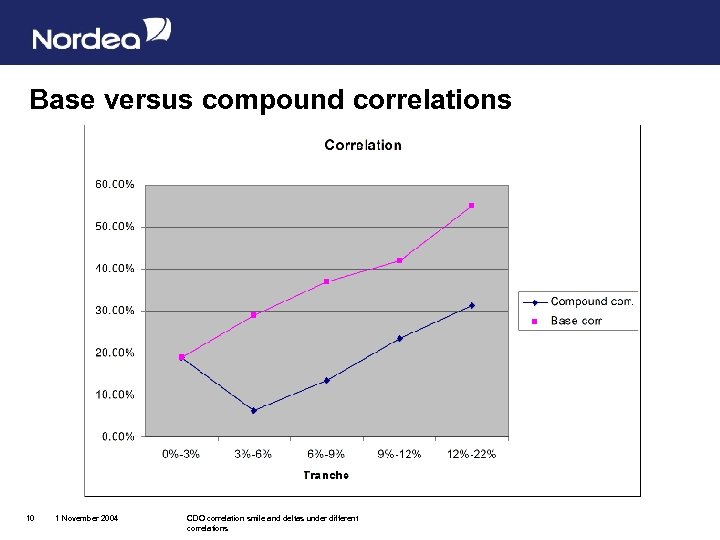Base versus compound correlations 10 1 November 2004 CDO correlation smile and deltas under different correlations

Delta hedges l CDO tranches typical traded with initial credit hedge l Conveniently quoted as amount of underlying index CDS to buy in order to hedge credit risk l Base correlation: find by long/short strategy l l 11 Base and compound correlation deltas are different 1 November 2004 CDO correlation smile and deltas under different correlations

What does the smile mean? l The presence of the smile means that the Gaussian copula does not describe market prices – Otherwise the correlation would have been constant over tranches and maturities l 12 How to fix this “problem”? 1 November 2004 CDO correlation smile and deltas under different correlations

Is base correlations a real solution? l No, it is merely a convenient way of describing prices l An intermediate step towards better models that exhibit a smile l No smile dynamics l Correlation smile modelling, versus l Models with a smile and correlation dynamics l So how to find a solution? 13 1 November 2004 CDO correlation smile and deltas under different correlations

In theory… l Sklar’s theorem: – Every simultaneous distribution of the survival times with marginals consistent with CDS prices can be described by the copula approach l So in theory we should just choose the correct copula, i. e. l Choose the correct simultaneous distribution of Xi. 14 1 November 2004 CDO correlation smile and deltas under different correlations

In practice however… l So far we have chosen from a rather limited set of copulas: s Gaussian, T-distribution, Archimedian copulas s A lot of parameters (correlation matrix) which we do not know how to choose s None of these have produced a smile that match market prices s Or the copulas have not provided the “correct” distributions 15 1 November 2004 CDO correlation smile and deltas under different correlations

So the search for better copulas has started. . . l “Better” means – describing the observed prices in the market for i. Traxx – produces a correlation smile – has a reasonable low number of parameters one can have a view on and interpret – has a plausible dynamics for the correlation smile – constant parameters can be used on a range of – tranches – maturities – (portfolios) l 16 Start from Gaussian model described as a 1 factor model 1 November 2004 CDO correlation smile and deltas under different correlations

Implementation of Gaussian copula l Factor decomposition: M, Zi independent standard Gaussian, Xi low early default l FFT/Recursive: – Given T: use independence conditional on M and calculate loss distribution analyticly, next integrate over M l 17 Simulation: – Simulate Ti, straight forward – Slower, in particular for risk, but more flexible – All credit risk can be calculated in same simulation run as the basic pricing 1 November 2004 CDO correlation smile and deltas under different correlations

Copulas with a smile, some posibilities l Start from factor model: l Let M and Zi have different distributions Hull & White, 2004: Uses T-4 distributions, seems to work well l Let a be random l Correlate M, Zi, a and RR in various ways Andersen & Sidenius, 2004 l Changes weight between systematic M and idiosyncratic Zi l Limits on variations as we still want nice mathematical properties l Distribution function H for Xi needed in all cases: Fi(Ti) = H(Xi) 18 1 November 2004 CDO correlation smile and deltas under different correlations

Andersen & Sidenius 2004, two point model Random Correlation Dependent on Market l Let a be a function of the market factor M l , m ensures var=1, mean=0 l Interpretation for > and small: Most often correlation is small, but in bad times we see a large correlation. Senior investors benefit from this. 19 1 November 2004 CDO correlation smile and deltas under different correlations

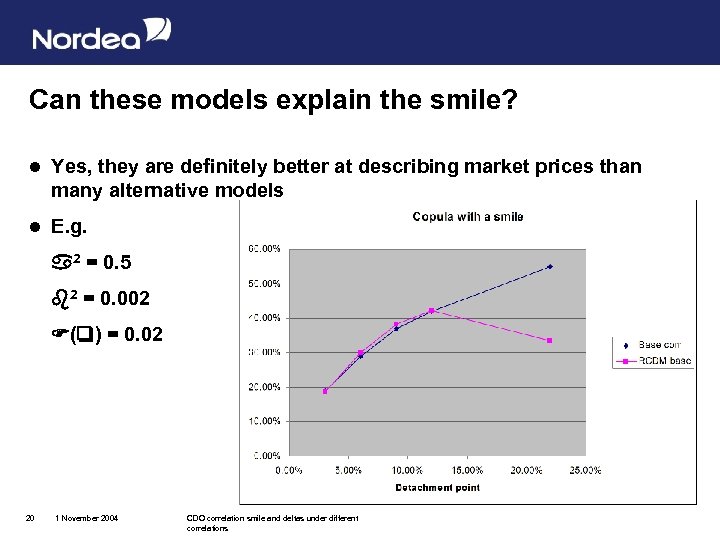Can these models explain the smile? l Yes, they are definitely better at describing market prices than many alternative models l E. g. 2 = 0. 5 2 = 0. 002 ( ) = 0. 02 20 1 November 2004 CDO correlation smile and deltas under different correlations

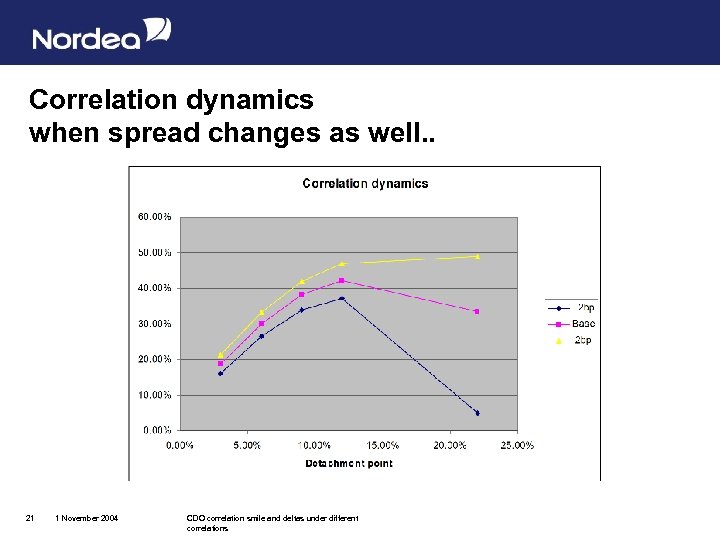Correlation dynamics when spread changes as well. . 21 1 November 2004 CDO correlation smile and deltas under different correlations

Delta with model generating smile l Deltas differ between models: l Agreement on delta amounts requires model agreement l New “market standard copula” will emerge? – Will have to be more complex than the Gaussian 22 1 November 2004 CDO correlation smile and deltas under different correlations

Different models has different deltas. . . l This does not necessarily imply any inconsistencies – On the other hand it might give problems! CDS spread l Different parameter spaces in different models give different deltas l 23 Model 2 We want models with stable parameters Makes it easier to hedge risk l Model 1 Corr/ /. . . Beware of parameters, say , moving when other parameters move: 1 November 2004 CDO correlation smile and deltas under different correlations

Conclusion l The market is still evolving fast l More and more information available l Models will have to be developed further – Smile description – Smile dynamics – Delta amounts – Bespoke tranches (no implied market) – Will probably go through a couple of iterations 24 1 November 2004 CDO correlation smile and deltas under different correlations