APPLYING SENSITIVITY ANALYSIS_RUS.pptx
- Количество слайдов: 31

Case 3: Изменения коэффициентов базисных переменных xj (при фиксированном j) является базисной переменной оптимального решения в окончательной симплекс таблице, изменения вносятся только в коэффициенты этой переменной. Симплекс таблица должна быть в надлежащей форме по методу исключения Гаусса (столбец небазисных переменных может быть состоять из каких угодно значений, поэтому Case 2 a не затрагивается). Для Case 3, коэффициент базисной переменной xj = 1 в своей строке и 0 в каждой второй строке (включая строку 0).

После того, как рассчитаны изменения в столбце xj окончательной симплекс таблицы, необходимо применить метод исключения Гаусса для восстановления этой формы. Это приведет к изменению значения текущего базисного решения, и оно станет либо невозможным, либо неоптимальным (поэтому требуется повторная оптимизация). Для Case 3 необходимы все этапы общей процедуры. До применения метода исключения Гаусса, формулы для пересмотра столбца xj такие же, как для случая 2 а.

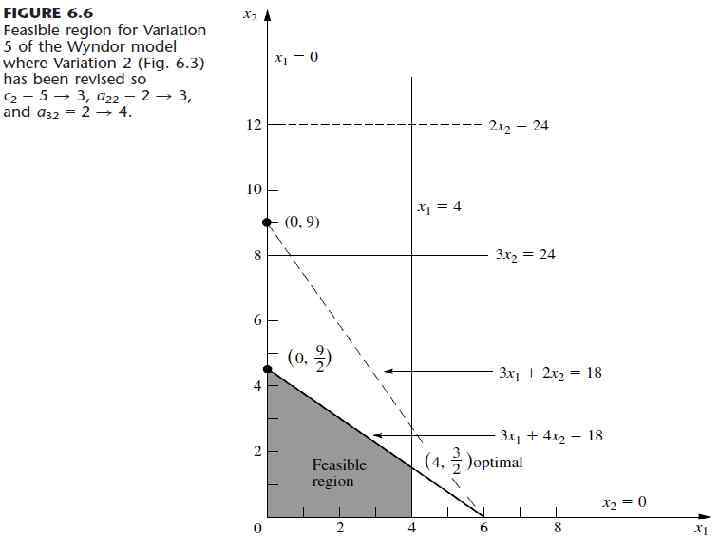
• Пример (вариант 5 модели задачи о заводе): Так как x 2 является базисной переменной для Варианта 2, его коэффициенты анализа чувствительности подходят для Case 3. Учитывая, что текущее оптимальное решение (x 1 = 0, x 2 = 9), продукт 2 единственный новый продукт, который вводится, и его производство должно быть относительно большим ключевым вопросом является то, переоценили ли первоначальные оценки, давшие коэффициенты x 2 текущей модели (вариант 2), привлекательность продукта 2. Проверка самых пессимистических оценок для этих коэффициентов (c 2 = 3, a 22 = 3, a 32 = 4) изменения, которые должны быть проанализированы (вариант 5):

• Графически это выражается в том, что изменяется область допустимых значений. Оптимальное решение (x 1, x 2) = (0, 9) - решение угловых точек, лежащих на пересечении границ ограничений x 1 = 0 and 3 x 1 + 2 x 2 = 18. Пересмотр ограничений соответствующее решение угловых точек (0, 9/2). Это решение больше не является оптимальным, поскольку пересмотренная целевая функция Z = 3 x 1 + 3 x 2 теперь дает новое оптимальное решение (x 1, x 2) = (4, 3/2).

• Анализ варианта 5. Так как единственные изменения в модели - изменения коэффициентов x 2, единственные изменения в окончательной симплекс таблице - в колонке x 2 используем формулы для повторного вычисления только в этом столбце.


• (Аналогично, может быть использован анализ приращения Δc 2 = -2, Δa 22 = 1, и Δa 32 = 2 таким же образом для того, чтобы получить этот столбец). Новые коэффициенты x 2 не имеют необходимых значений, поэтому на следующем этапе необходимо преобразование в надлежащую форму по методу исключения Гаусса (делением строки 2 на 2, вычитая 7 раз новую строку 2 от строки 0, добавляя новую строку 2 к строке 3). Получившаяся вторая таблица дает новое значение текущего базисного решения, x 3 = 4, x 2 = 9/2 , x 4 = 21/2(x 1 = 0, x 5 = 0), переменные неотрицательны решение все еще допустимо. x 1 имеет отрицательный коэффициент в строке 0 оно уже неоптимальное.

• Чтобы найти новое оптимальное решение, применим симплекс-метод, взяв это решение в качестве исходного ОД решения. Исходная введенная переменная x 1, в то время как x 3 уходящая переменная. Здесь необходима одна итерация для достижения нового оптимального решения x 1 = 4, x 2 = 3/2, x 4 = 39/2 (x 3 = 0, x 5 = 0). Данный анализ предполагает, что c 2, а 22, а 32 относительно чувствительные параметры. Дополнительные данные для их более точной оценки получены только путем запуска пробной партии производство продукта 2 рекомендовано начать сразу же, и в малых масштабах (x 2 = 3/2). Этот опыт использовался для управления решением о том, куда должны быть выделены оставшиеся производственные мощности - на продукт 2 или продукт 1.

• Допустимый диапазон для сохранения оптимальности. Если xj является базисной переменной, необходимо преобразование в надлежащую форму по методу исключения Гаусса перед проверкой на оптимальность. Учитывая вариант 5 модели с (c 2 = 3, a 23 = 4). Так как х2 является базисной переменной для оптимального решения (c 2 = 3), шаги, необходимые, чтобы найти допустимый диапазон для сохранения оптимальности для с2:

• 1. Коэффициент базисной переменной x 2 в новой окончательной строке 0 автоматически становится z 2* - c 2 = 0 до того, как c 2 изменяется от своего текущего значения до 3. 2. Увеличение c 2 = 3 by ∆c 2 (so c 2 = 3 + ∆c 2). Это приводит к изменению коэффициента: z 2* - c 2 = ∆c 2, что меняет строку 0 на Строку 0 = [0, -∆c 2, 3/4, 0, 3/4, 33/2]. 3. С ненулевым коэффициентом, восстановим надлежащий вид по методу исключения Гаусса. Для получения новой строки 0, надо прибавить к строке 0 произведение Δc 2 и строки 2.

• 4. Используя эту новую строку 0, найдем такое решение для диапазона значений Δc 2, при котором коэффициенты небазисных переменных (x 3 и x 5) остаются неотрицательными. 5. Так как с2 = 3 + Δc 2, прибавим 3 к этому диапазону значений, что дает 0 ≤ c 2 ≤ 4 в качестве допустимого диапазона для сохранения оптимальности для c 2.

• Целевая функция Z = 3 x 1 + c 2 x 2, текущее значение c 2 = 3 оптимальное решение (4, 3/2). При увеличении c 2, решение остается оптимальным только для c 2 ≤ 4. Для c 2 ≥ 4, (0, 9/2) становится оптимальным (при c 2 = 4), из-за границ ограничений 3 x 1 + 4 x 2 = 18. Если c 2 уменьшается, (4, 3/2) остается оптимальным только для c 2 ≥ 0. Для c 2 ≤ 0, (4, 0) становится оптимальным из-за границы ограничения x 1 = 4. Допустимый диапазон для сохранения оптимальности для c 1 (при c 2 = 3) может быть получен либо алгебраически или графически, чтобы c 1 ≥ 9/4 допустимое уменьшение для c 1 от текущего значения 3 возможно только до 3/4.

• Можно уменьшить c 1 на большую величину, не изменяя оптимального решения, если c 2 также уменьшается на достаточную величину. Например, предположим, что c 1 и c 2 снизились на 1 от текущего значения 3, так что целевая функция изменяется от Z = 3 x 1 + 3 x 2 до Z = 2 x 1 + 2 x 2. В соответствии с правилом 100% для одновременных изменений в коэффициентах целевой функции, процент допустимых изменений - 133 1/3% и 33 1/3%, их сумма превышает 100%. Наклон линии целевой функции не изменился, поэтому (4, 3/2) попрежнему является оптимальным.

• Case 4: Введение нового ограничения Введение в модель после ее решения, поскольку ограничение изначально было упущено или потому, что возникли новые обстоятельства, после того как была сформулирована модель. Или ограничение было намеренно удалено, чтобы снизить вычислительные затраты, поскольку оно было менее ограничивающим, чем другие. Но теперь оно должно быть сверено с полученным оптимальным решением. Чтобы убедиться, что текущее оптимальное решение будет затронуто новым ограничением, нужно непосредственно проверить, удовлетворяет ли оптимальное решение ограничению.

• Если это так, то оно все равно останется лучшим допустимым решением (т. е. оптимальным решением). Новое ограничение может только устранить некоторые ранее допустимые решения без добавления каких-либо новых. Если новое ограничение на самом деле устраняет текущее оптимальное решение, и вы хотите найти новое решение, надо ввести это ограничение в окончательную симплекс таблицу (в качестве дополнительной строки) так же, как если бы это была исходная таблица, где обычные дополнительные переменные (фиктивные переменные или искусственные переменные) будут использоваться в качестве основных переменных для этой новой строки.

• Поскольку новая строка будет иметь ненулевые коэффициенты для некоторых других базисных переменных, на следующем этапе выполняется преобразование в надлежащую форму по Гауссу, а затем повторная оптимизация. Вопрос в том, является ли ранее оптимальное решение все еще допустимым, так что шаг 5 (проверка на оптимальность) опускается. Шаг 4 (анализ допустимости) заменен на более быструю проверку на допустимость (удовлетворяет ли ранее оптимальное решение новым ограничениям? ) выполняется после шага 1 (пересмотр модели). Только в том случае, если эта проверка дает отрицательный ответ, и нужна повторная оптимизация, используются шаги 2, 3 и 6 (пересмотр окончательной таблицы, преобразование в надлежащую форму по Гауссу и повторная оптимизация).

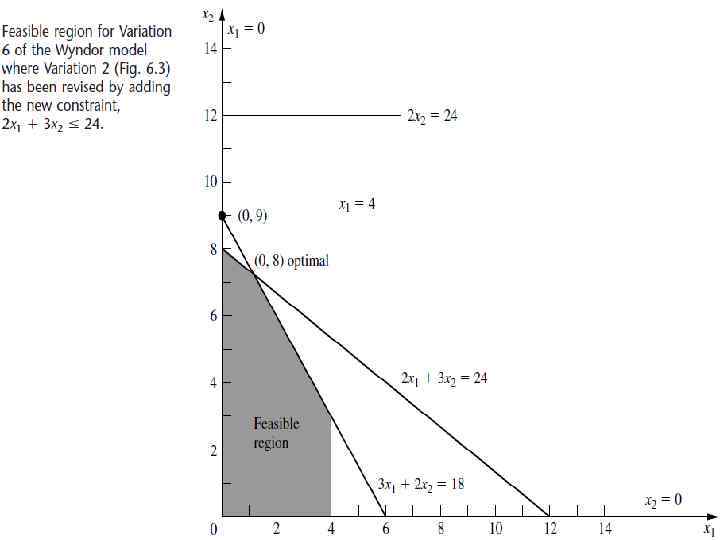
• Пример (вариант 6). Вводим новые ограничения 2 x 1 + 3 x 2 ≤ 24 в вариант 2 модели. Предыдущее оптимальное решение (0, 9) нарушает новое ограничение, поэтому оптимальное решение меняется на (0, 8). (0, 9) дает 2 x 1 + 3 x 2 = 27 > 24, так что это предыдущее оптимальное решение не является больше допустимым. Таким образом, добавляем новые ограничения в текущую окончательную симплекс таблицу, с фиктивной переменной x 6 в качестве исходной базисной переменной. Преобразование в надлежащую форму по Гауссу требует вычитания из новой строки произведения, 3 умножить на строку 2, которая определяет текущее базисное решение x 3 = 4, x 2 = 9, x 4 = 6, x 6 = -3 (x 1 = 0, x 5 = 0), как показано на второй таблицы. Применение двойственного симплекс-метода приводит к новому оптимальному решению только за одну итерацию.


Систематический анализ чувствительности Параметрическое программирование: Другой подход к анализу чувствительности заключается в изменении одного или нескольких параметров непрерывно на протяжении некоторого интервала, чтобы увидеть, когда изменится оптимальное решение. В варианте 2, вместо анализа отдельных изменений от b 2 = 12 до =24, положим = 12 +θ и непрерывно изменяем θ от 0 до 12. Линия ограничения 2 х2 = 12 смещается вверх до 2 x 2 = 12+θ, при увеличении от 0 до 12. Результат в том, что исходное оптимальное решение УДТ (2, 6) сдвигает линию ограничения 3 x 1 + 2 x 2 =18 до (-2, 12). Это решение остается оптимальным до тех пор, пока оно допустимо (x 1 = 0), после чего (0, 9) становится оптимальным решением. Алгебраические расчеты влияния ∆b 2 =θ аналогичны для случая 1 - пример, где Δb 2 = 12. Мы используем выражения для Z * и b* для случая 1

где сейчас И где y* и S* даны в середине таблицы в рамочке. Эти уравнения показывают, что оптимальное решение

• - это для θ небольших настолько, что данное решение все еще является допустимым, то есть для θ ≤ 6. Для θ> 6, двойственный симплекс-метод выдает таблицу, за исключением значения x 4. Таким образом, Z = 45, x 3 = 4, х2 = 9 (x 1 = 0, x 5 = 0), и выражение для b* дает x 4 = b 3 = 0 (4) + 1 (12 + θ) - 1 (18 ) = -6 + θ. Эта информация может быть использована (с другими данными, не входящими в модель по увеличению b 2), чтобы решить, следует ли сохранить исходное оптимальное решение и, если нет, насколько увеличить b 2. Мы можем исследовать влияние изменения сразу нескольких параметров на оптимальное решение. Когда мы меняем только параметры bi, мы выражаем новое значение bi , используя исходное bi следующим образом: для i 1, 2, . . . , m, где значения ai – введенные константы , устанавливающие желаемый уровень повышения (положительный или отрицательный) соответствующей правой части при увеличении θ.

• Предположим, что можно переместить часть производства текущего продукта с завода 2 на завод 1, тем самым увеличивая b 2 за счет уменьшения b 3. Также предположим, что b 3 уменьшается вдвое быстрее, чем увеличивается b 2. Тогда • Где (неотрицательное) значение θ измеряет измененный объем производства. ( a 1=0, a 2=1, a 3=-2) Геометрический смысл в том, что увеличиваясь от 0, ограничительная линия 2 x 2 = 12 перемещается к 2 x 2 = 12 +θ (игнорируя линию 2 x 2 = 24) и одновременно линия ограничения 3 x 1 + 2 x 2 = 18 перемещается вниз к 3 x 1 + 2 x 2 = 18 - 2θ.

• Оригинальный оптимальное решение УДТ (2, 6) лежит на пересечении линий 2 x 2 = 12 и 3 x 1 + 2 x 2 = 18, так смещение этих линий вызывает смещение этого решения угловых точек. Целевая функция Z = 3 x 1 + 5 x 2 решение остается оптимальным, пока оно допустимо (x 1 ≥ 0). Изменение b 2 и b 3 включает использование формул Варианта 1 (при неизвестном θ) для расчета окончательных изменений в окончательной таблице:

Оптимальное решение: - Это для θ, настолько небольших, что это решение все еще допустимо, т. e. , для θ≤ 2. Z уменьшается, в то время как θ увеличивается от 0. Это что лучший выбор для θ θ= 0, поэтому не следует перемещать производство. Изменяя несколько параметров cj одновременно одинаково. Мы выражаем новое значение используя исходное cj как для j 1, 2, . . . , n, где значения ai – введенные константы , устанавливающие желаемый уровень повышения (положительный или отрицательный) соответствующей правой части при увеличении θ. Нужно пересмотреть анализ чувствительности c 1 и c 2 для задачи о заводе, выполненный ранее.

Начиная с Варианта 2 мы рассмотрели влияние изменения c 1 от 3 до 4 (самые оптимистичные оценки) и c 2 от 5 до 3 (самые пессимистические оценки). Теперь можно одновременно рассматривать оба изменения, а также различные промежуточные случаи с меньшими изменениями, установив • где значение θ измеряет долю от максимально возможного изменения, которые сделаны. Результат состоит в замене исходной целевой функции Z = 3 x 1 + 5 x 2 на функцию от θ Z(θ) = (3 + θ)x 1 + (5 - 2θ)x 2,

• Оптимизация может быть выполнена для любого желаемого значения θ между 0 и 1. Проверяя влияние увеличения θ, когда оно возрастает от 0 до 1, мы выясним, когда и как меняется оптимальное решение при увеличении ошибки в первоначальной оценке этих параметров. Логично учитывать эти изменения одновременно, если есть факторы, которые заставляют параметры изменяться совместно. Конкурируют ли продукты между собой, так что большая прибыль на единицу продукции одного предполагает меньшую прибыль на единицу продукции для другого? Влияют ли на них такие факторы, как реклама конкурента? Можно ли одновременно изменить прибыль от обоих за счет соответствующего смещения персонала и оборудования? В области допустимых значений, геометрическая интерпретация изменения целевой функции от Z = 3 x 1 +5 x 2 до to Z(θ) = (3+θ )x 1+(5 -2θ)x 2 - то, что мы изменяем наклон линии исходной целевой функции (Z = 45 = 3 x 1 + 5 x 2), которая проходит через оптимальное решение (0, 9).

• Если θ увеличивается достаточно, этот наклон будет меняться, так оптимальное решение перейдет от (0, 9) к другому решению УДТ (4, 3) (проверка θ ≤ 1). Хотя изменения выражены через θ, а не конкретные численные суммы, θ рассматривается как неизвестное число. Таблица отображает соответствующие строки (строка 0 и строка для основной переменной x 2). Первая показанная таблица - окончательная таблица для текущей версии модели (до того, как изменены c 1 и c 2). Только изменения в пересмотренной окончательной таблице показаны дальше - Δc 1 и Δc 2 вычитаются из строки 0 коэффициентов x 1 и x 2. Для преобразования этой таблицы в надлежащую форму по Гауссу, мы вычитаем 2θ умноженное на строку 2 из строки 0, что дает последнюю таблицу.
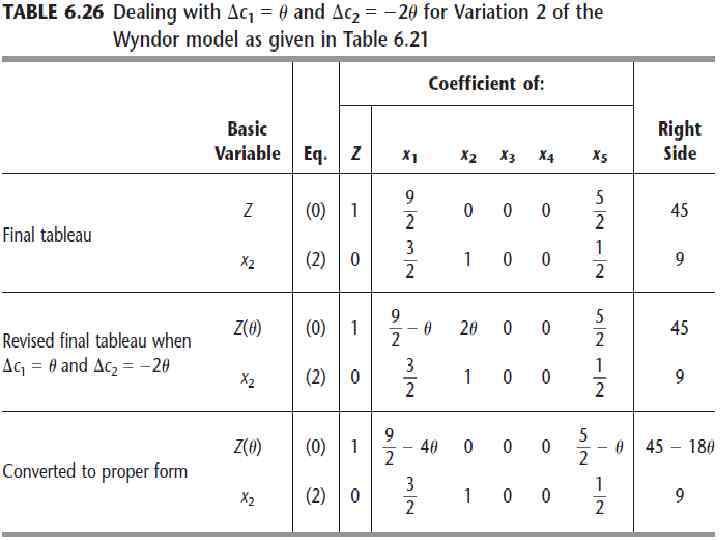

Выражения через θ для коэффициентов неосновных переменных x 1 и x 5 в строке 0 этой таблицы показывают, что текущее ОД решение остается оптимальным для θ ≤ 9/8. Так как θ = 1 является максимальным значением, это означает, что c 1 и c 2 вместе являются нечувствительными параметрами по отношению к Варианту 2 модели. Не нужно оценивать эти параметры более точно, если только не будут меняться другие параметры (как в варианте 5). Этот способ непрерывного изменения нескольких параметров одновременно называется параметрическим линейным программированием.
APPLYING SENSITIVITY ANALYSIS_RUS.pptx