Cascade Physics at Ba Bar and Glue X

Cascade Physics at Ba. Bar and Glue. X with Selected LASS-Glue. X Comparisons Veronique Ziegler (SLAC) Glue. X Workshop Jefferson Lab, March 6 -8, 2008 1

Overview 1. Relevance of Cascades to Baryon Spectroscopy 2. Cascade Physics from Charm Baryon Decay (*) • Ba. Bar as a Charm Baryon Factory • Measurement of the W- spin [PRL 97, 112001 (2006)] • • Motivation for quasi-two-body approach to Cascade Resonance study Application to Lc+ → K+ X(1530)0, X(1530)0 → X- + • • Dalitz plot [to be submitted to Phys. Rev. D] Application to Lc+ → K+ X(1690)0, X(1690)0 → L K 0 • • Measure X(1530) spin; shortcomings of quasi-two-body approach; need for understanding of entire Quasi-two-body approach again inadequate; performed full Dalitz plot analysis [Proceedings of MENU & NSTAR conferences; Phys. Rev. D article in preparation] Comparison of Detector Characteristics Relevant to Cascade Physics • Ba. Bar − Glue. X • LASS − Glue. X Possible Cascade Studies with Glue. X Summary 2 ==================================================================== Note: The inclusion of charge conjugate states is implied for Ba. Bar analyses. (*)Ph. D. Thesis: SLAC-R-868

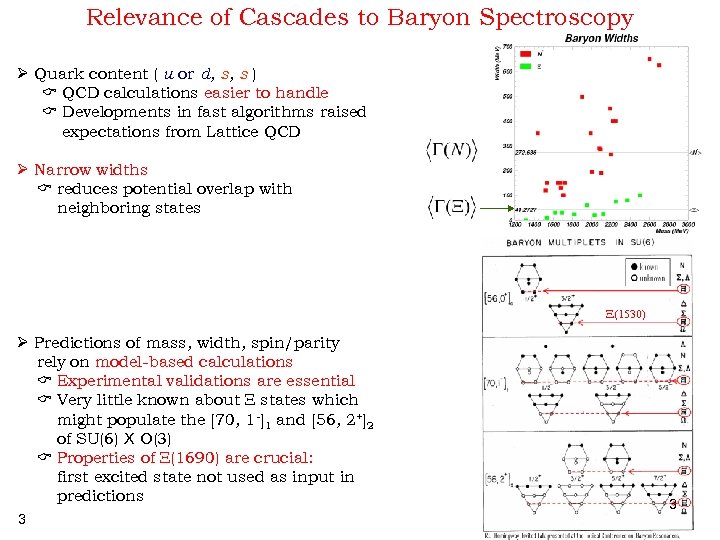
Relevance of Cascades to Baryon Spectroscopy Ø Quark content ( u or d, s, s ) QCD calculations easier to handle Developments in fast algorithms raised expectations from Lattice QCD Ø Narrow widths reduces potential overlap with neighboring states X(1530) Ø Predictions of mass, width, spin/parity rely on model-based calculations Experimental validations are essential Very little known about X states which might populate the [70, 1 -]1 and [56, 2+]2 of SU(6) X O(3) Properties of X(1690) are crucial: first excited state not used as input in predictions 3 3

Cascade Physics from Charm Baryon Decay 4

Ba. Bar as a Charm Baryon Factory Present data sample contains = s L) : (N > 490 M U(4 S) → BB events(s = 1. 05 nb) > 1500 > M e+e- Excellent → qq events (s = 3. 39 nb) resolution 600 M e+e- → cc events (s = 1. 30 nb) Charm Baryon (& Meson) Factory High statistics charm baryon production Large Samples of Charm Baryon Two-body & Quasi-two-body Decays Rare Decay Modes Accessible with Reasonable Statistics Hyperon & Hyperon Resonance Cottage Industry 5 Can Study Hyperon & Hyperon Resonance properties with high precision e. g. W- Spin [PRL 97, 112001(2006)]] 5

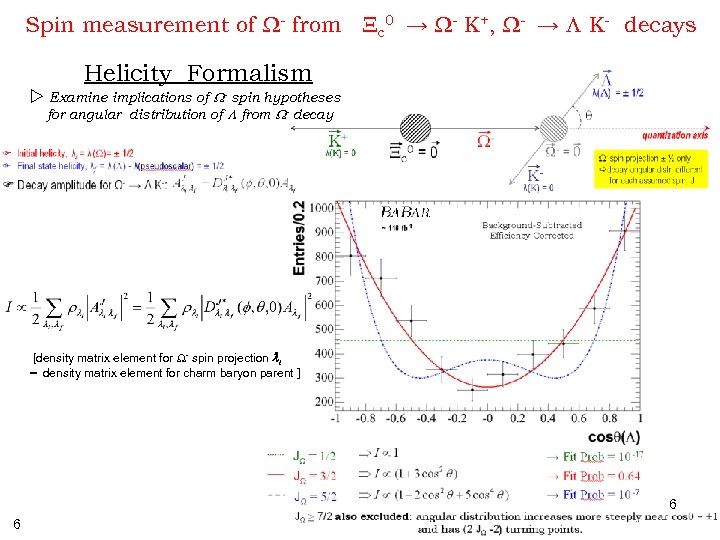
Spin measurement of W- from Xc 0 → W- K+, W- → L K- decays Helicity Formalism w Examine implications of W- spin hypotheses for angular distribution of L from W- decay [density matrix element for W- spin projection li = density matrix element for charm baryon parent ] 6 6

The X(1530)0 From Lc+ → X- + K+ Decay 7

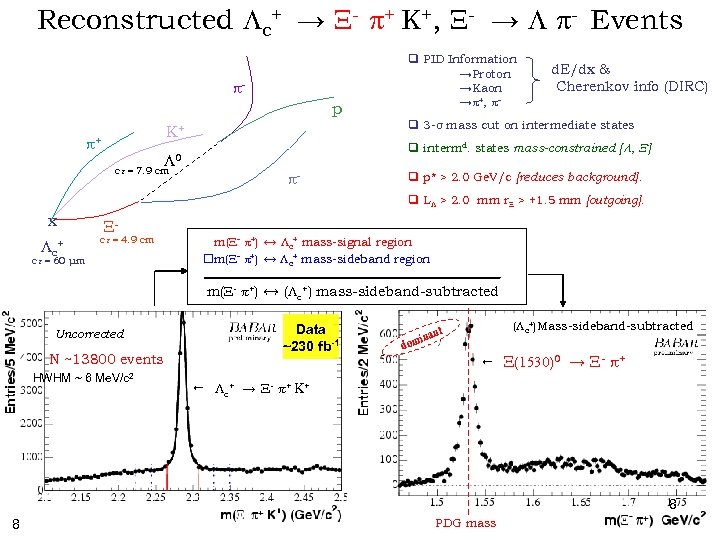
Reconstructed Lc+ → X- + K+, X- → L - Events q PID Information →Proton →Kaon → +, - p q 3 -σ mass cut on intermediate states K+ + d. E/dx & Cherenkov info (DIRC) q intermd. states mass-constrained [ L, X-] L 0 ct = 7. 9 cm - q p* > 2. 0 Ge. V/c [reduces background]. q LL > 2. 0 mm r. X > +1. 5 mm [outgoing]. x Lc + X- ct = 4. 9 cm ct = 60 μm m(X- +) ↔ Lc+ mass-signal region m(X- +) ↔ Lc+ mass-sideband region . . m(XUncorrected N ~13800 events HWHM ~ 6 Me. V/c 2 +) ↔ (Lc+) mass-sideband-subtracted Data ~230 fb-1 d nt mina o (Lc+)Mass-sideband-subtracted X(1530)0 → X- + Lc+ → X- + K+ 8 8 PDG mass

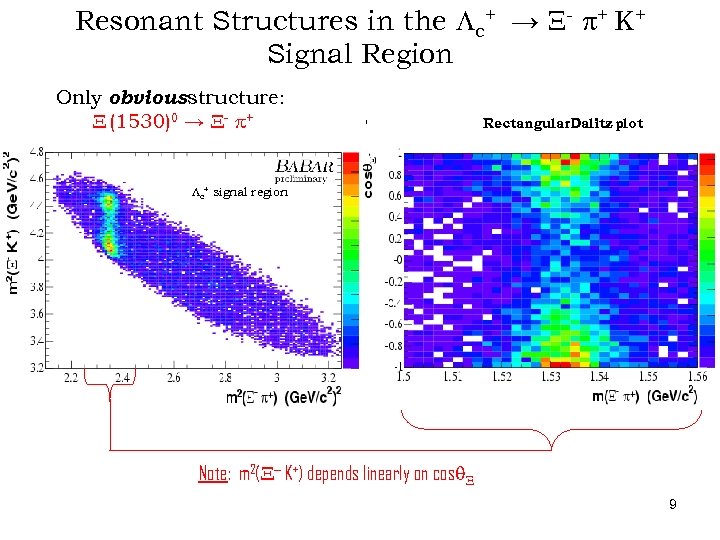
Resonant Structures in the Lc+ → X- + K+ Signal Region Only obviousstructure: X (1530)0 → X- + Rectangular. Dalitz plot Lc+ signal region Note: m 2(X- K+) depends linearly on cosq. X 9

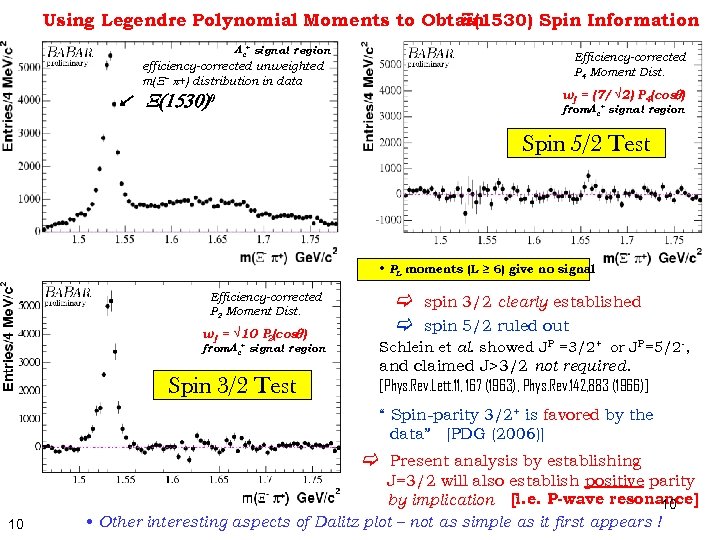
Using Legendre Polynomial Moments to Obtain X(1530) Spin Information Lc+ signal region efficiency-corrected unweighted m(X- p+) distribution in data Efficiency-corrected P 4 Moment Dist. wj = (7/ √ 2) P 4(cosq) X(1530)0 from. Lc+ signal region Spin 5/2 Test • PL moments (L ≥ 6) give no signal Efficiency-corrected P 2 Moment Dist. wj = √ 10 P (cosq) 2 from. Lc+ signal region Spin 3/2 Test spin 3/2 clearly established spin 5/2 ruled out Schlein et al. showed JP =3/2+ or JP=5/2 -, and claimed J>3/2 not required. [Phys. Rev. Lett. 11, 167 (1963), Phys. Rev. 142, 883 (1966)] “ Spin-parity 3/2+ is favored by the data” [PDG (2006)] 10 Present analysis by establishing J=3/2 will also establish positive parity by implication [i. e. P-wave resonance] 10 • Other interesting aspects of Dalitz plot – not as simple as it first appears !

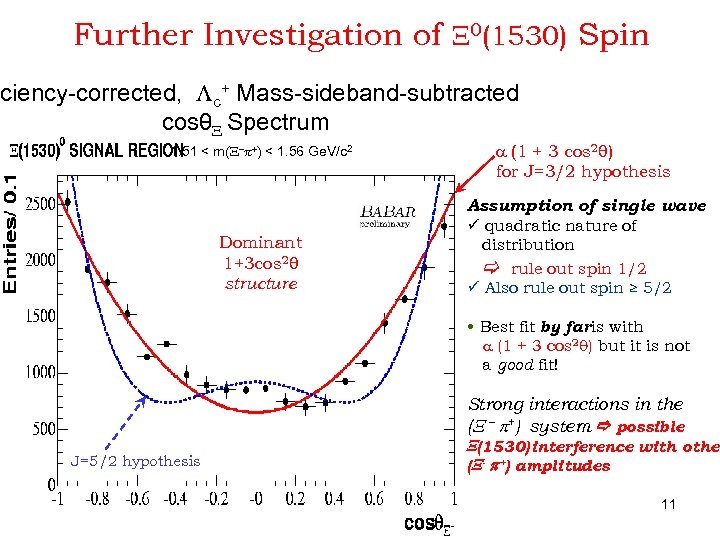
Further Investigation of X 0(1530) Spin iciency-corrected, Lc+ Mass-sideband-subtracted cosθX Spectrum 1. 51 < m(X- +) < 1. 56 Ge. V/c 2 Dominant 1+3 cos 2θ structure a (1 + 3 cos 2θ) for J=3/2 hypothesis Assumption of single wave ü quadratic nature of distribution rule out spin 1/2 ü Also rule out spin ≥ 5/2 • Best fit by far is with a (1 + 3 cos 2θ) but it is not a good fit! Strong interactions in the (X – p+) system possible J=5/2 hypothesis X(1530) interference with other (X- p+) amplitudes 11

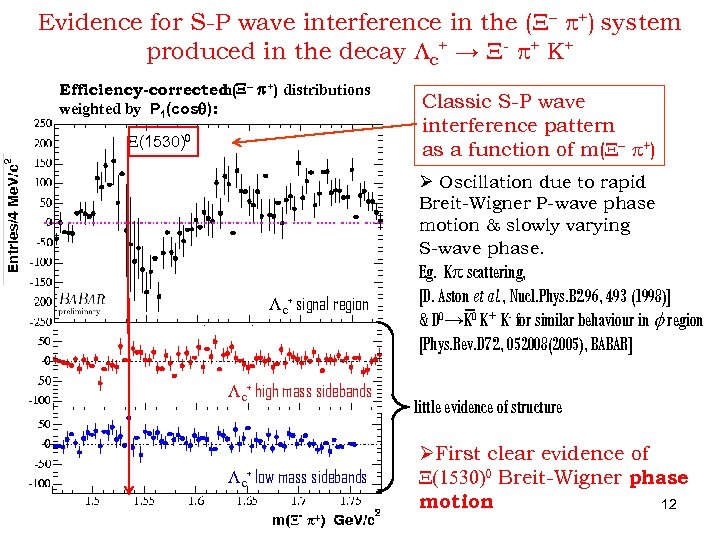
Evidence for S-P wave interference in the (X- +) system produced in the decay Lc+ → X- + K+ Efficiency-corrected - p+) distributions m(X weighted by P 1(cosq): X(1530)0 Classic S-P wave interference pattern as a function of m(X- +) Ø Oscillation due to rapid Breit-Wigner P-wave phase motion & slowly varying S-wave phase. Lc+ signal region Lc+ high mass sidebands Lc+ low mass sidebands Eg. K scattering, [D. Aston et al. , Nucl. Phys. B 296, 493 (1998)] & D 0→K 0 K+ K- for similar behaviour in f region [Phys. Rev. D 72, 052008(2005), BABAR] little evidence of structure ØFirst clear evidence of X(1530)0 Breit-Wigner phase motion 12

Partial wave amplitude description of the (X- +) system produced in the decay Lc+ →→ X + K+ Amplitudes of the (X- +) system: (X(1530)) & (non-resonant) Angular distribution of the X- produced in the decay of the (X- +) system: Total Intensity I = 13

Helicity Formalism Relationship between |L, S> states & helicity states [M. Jacob & C. G. Wick On the General Theory of Collisions for Particles with Spin Annals of Physics 7, 401 (1959)] AJl in terms of S, P, D waves J=1/2 J=3/2 Interference (Assuming r 1/2= r-1/2) S-P interf. Cannot distinguish P-D interf. between (S 1/2 + P 3/2) nor between (P 3/2 + D 3/2) [ Minami ambiguity ] ~ however strong P 3/2 wave suggests term containing S 1/2, P 3/2 amplitudes dominates simple model assuming only S 1/2 and P 3/2 amplitudes Try 14

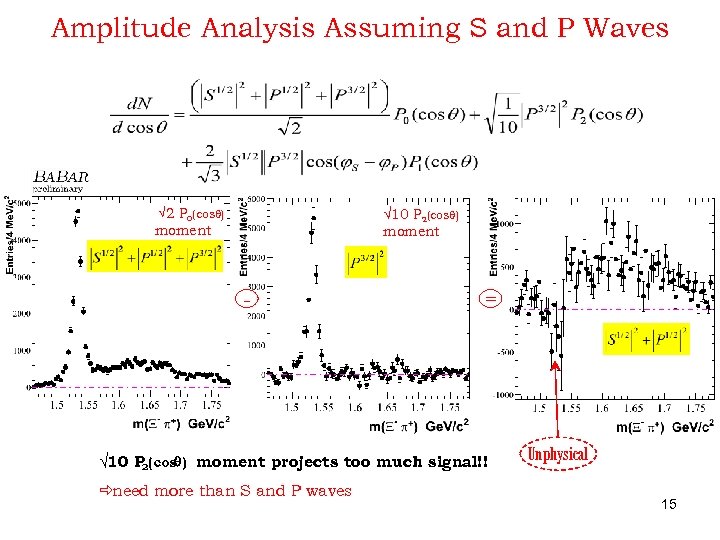
Amplitude Analysis Assuming S and P Waves √ 2 P 0(cosq) √ 10 P 2(cosq) moment - = √ 10 P 2(cosq) moment projects too much signal!! ðneed more than S and P waves Unphysical 15

Implication of Fits to the X(1530)0 Lineshape Efficiency-corrected P 2(cosq) moment P-wave BW Efficiency-corrected P 0(cosq) moment 4 P-wave BW 4 mi p. q S ai mi P-wave BW p. q S ai i=1 PDG ( m, G ) Data - Fit Residuals Poor fit due to interference with other waves? i=1 PDG ( m, G ) Data - Fit Effect should disappear in P 0(cosq) moment distribution Data - Fit Residuals Data - Fit Expected improvement in fit quality not realized Structure in X- K+ i. e. another isobar ? Or (K+p+) I=3/2 amplitude contribution? 16

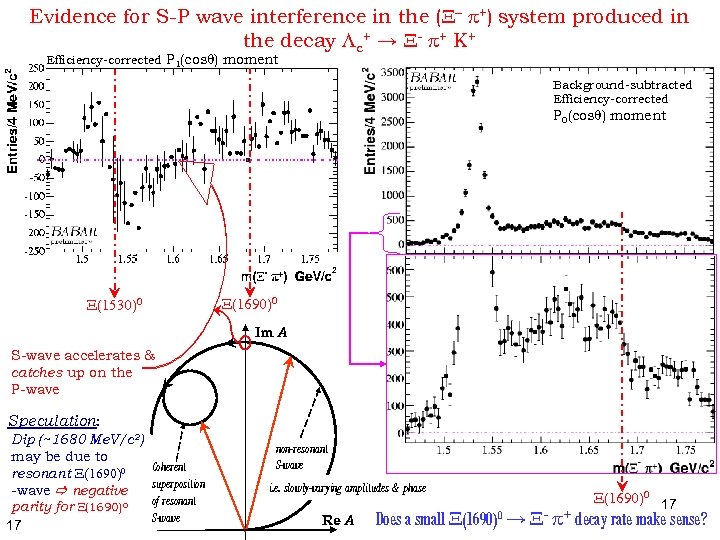
Evidence for S-P wave interference in the (X- +) system produced in the decay Lc+ → X- + K+ Efficiency-corrected P 1(cosq) moment Background-subtracted Efficiency-corrected P 0(cosq) moment X(1690)0 X(1530)0 Im A S-wave accelerates & catches up on the P-wave Speculation: Dip (~1680 Me. V/c 2) may be due to resonant X(1690)0 -wave negative parity for X(1690)0 17 Coherent S superposition of resonant S-wave non-resonant S-wave i. e. slowly-varying amplitudes & phase Re A X(1690)0 17 Does a small X(1690)0 → X- + decay rate make sense?

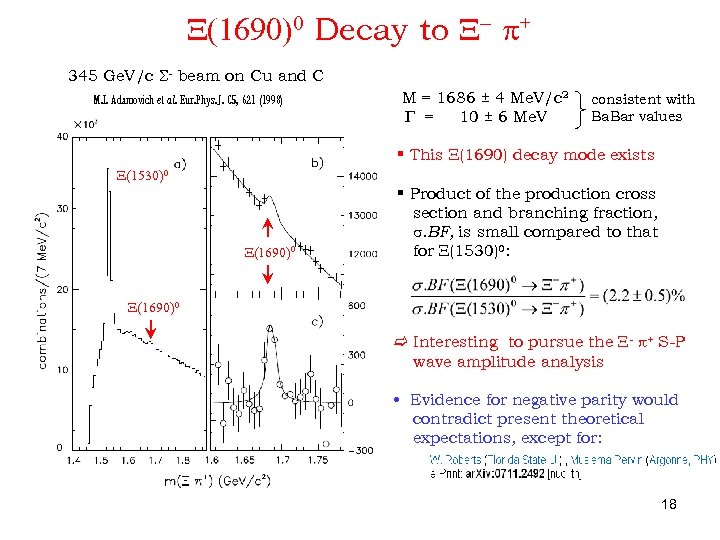
X(1690)0 Decay to X- + 345 Ge. V/c S- beam on Cu and C M. I. Adamovich et al. Eur. Phys. J. C 5, 621 (1998) M = 1686 ± 4 Me. V/c 2 G = 10 ± 6 Me. V consistent with Ba. Bar values § This X(1690) decay mode exists X(1530)0 X(1690)0 § Product of the production cross section and branching fraction, s. BF, is small compared to that for X(1530)0: X(1690)0 Interesting to pursue the X- + S-P wave amplitude analysis • Evidence for negative parity would contradict present theoretical expectations, except for: 18

The X(1690)0 From Lc+ → L K 0 K+ Decay 19

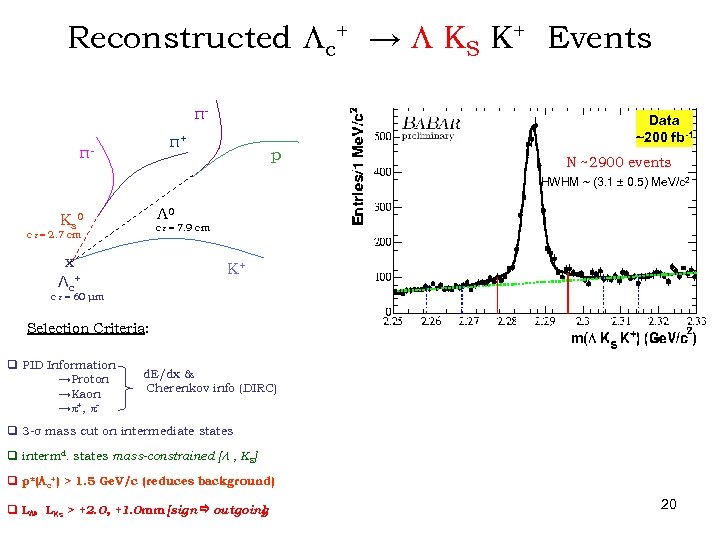
Reconstructed Lc+ → L KS K+ Events π- Data ~200 fb-1 π+ π- p N ~2900 events HWHM ~ (3. 1 ± 0. 5) Me. V/c 2 Λ 0 Ks 0 ct = 7. 9 cm ct = 2. 7 cm x Λ c+ K+ ct = 60 μm Selection Criteria: q PID Information →Proton →Kaon → +, - d. E/dx & Likelihood Selectors Cherenkov info (DIRC) q 3 -σ mass cut on intermediate states q intermd. states mass-constrained [ L , KS] q p*(Lc+) > 1. 5 Ge. V/c (reduces background) q LL, LKs > +2. 0, +1. 0 mm [sign outgoing ]. 20

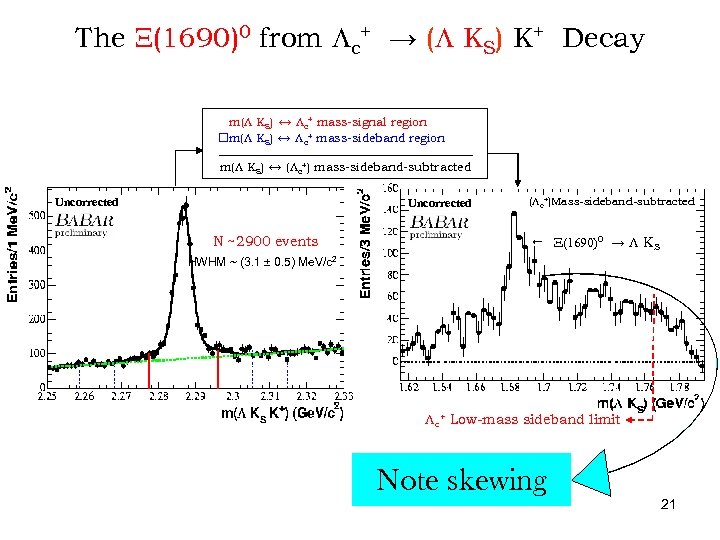
The X(1690)0 from Lc+ → (L KS) K+ Decay m(L KS) ↔ Lc+ mass-signal region m(L KS) ↔ Lc+ mass-sideband region. m(L KS) ↔ (Lc +) . mass-sideband-subtracted Uncorrected N ~2900 events (Lc+)Mass-sideband-subtracted X(1690)0 → L KS HWHM ~ (3. 1 ± 0. 5) Me. V/c 2 Lc+ Low-mass sideband limit Note skewing 21

Using Legendre Polynomial Moments to Obtain X(1690) Spin Information ▬ efficiency-corrected, background-subtracted unweightedm(L KS) distribution in data wj = (7/ √ 2) P 4(cosq) from. Lc+ signal region Spin 5/2 Test X(1690) → 0 ) ] 90 6 wj = √ 10 P (cosq) 2 from. Lc+ signal region Efficiency-corrected P 4 Moment Dist. Efficiency-corrected P 2 Moment Dist. Spin 3/2 Test t Su s ge J( 1 X[ 2 1/ = efficiency-corrected, bckgr. -subtracted dist. in data for 1. 665<m(L KS)<1. 705 Ge. V/c 2 g …however cosq. L clearly not flat as expected for J = 1/2 22 WHY? 22

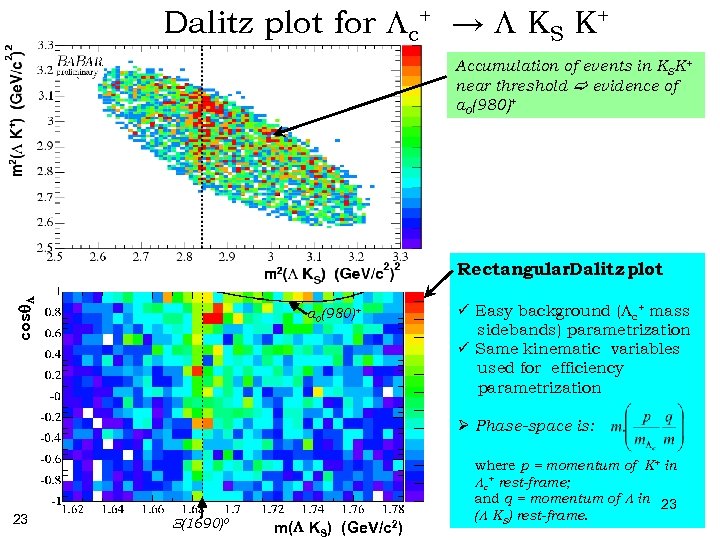
Dalitz plot for Lc+ → L KS K+ Accumulation of events in KSK+ near threshold evidence of a 0(980)+ cosq. L Rectangular. Dalitz plot a 0(980)+ ü Easy background (Lc+ mass sidebands) parametrization ü Same kinematic variables used for efficiency parametrization Ø Phase-space is: 23 X(1690)0 m(L KS) (Ge. V/c 2) where p = momentum of K+ in Lc+ rest-frame; and q = momentum of L in 23 (L KS) rest-frame.

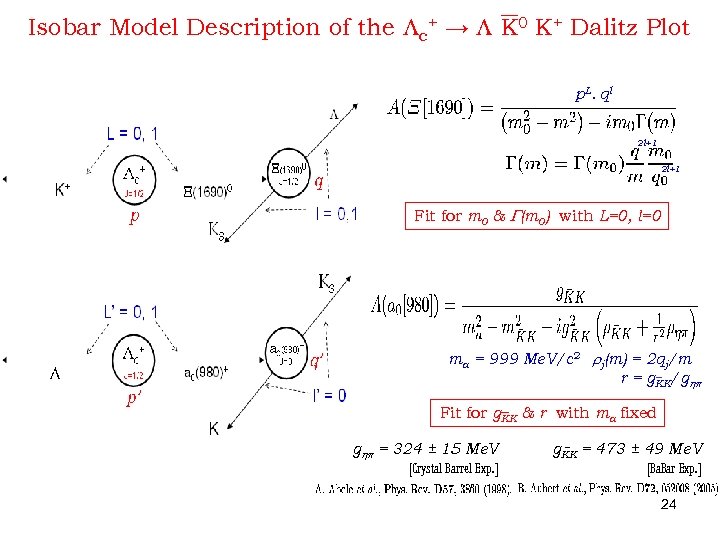
Isobar Model Description of the Lc+ → L K 0 K+ Dalitz Plot p L. q l 2 l+1 Fit for m 0 & G(m 0) with L=0, l=0 ma = 999 Me. V/c 2 rj(m) = 2 qj/m r = g. KK/ghp Fit for g. KK & r with ma fixed ghp = 324 ± 15 Me. V [Crystal Barrel Exp. ] g. KK = 473 ± 49 Me. V [Ba. Bar Exp. ] 24

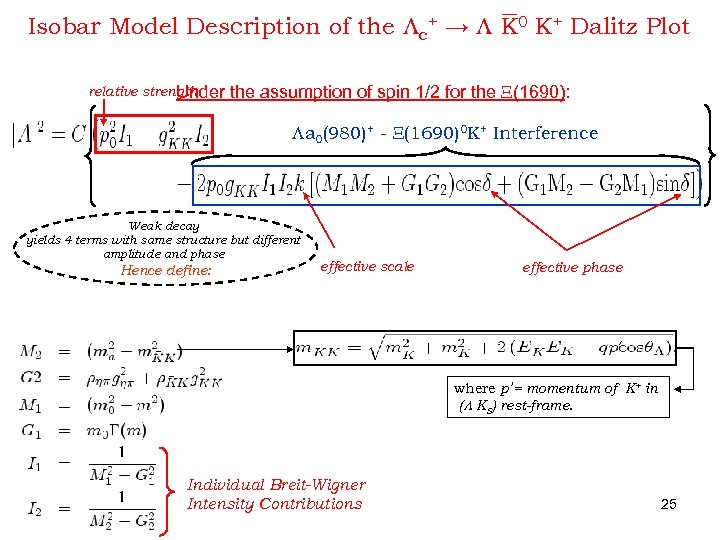
Isobar Model Description of the Lc+ → L K 0 K+ Dalitz Plot relative strength Under the assumption of spin 1/2 for the X(1690): La 0(980)+ - X(1690)0 K+ Interference Weak decay yields 4 terms with same structure but different amplitude and phase Hence define: effective scale effective phase ‘ where p’ = momentum of K+ in (L KS) rest-frame. Individual Breit-Wigner Intensity Contributions 25

Comparison of. Max. Likelihood Fit Result the Signal Projections to For J(X[1690]) = 1/2 1. 615 < m(LKs) < 1. 765 Ge. V/c 2 Excellent reproduction of skewed lineshape and of cosq. L distribution Background-subtracted, efficiency-corrected data ― Integrated signal function smearedby mass resolution [Histogram] ― Signal function with no resolution smearing ― |A(a 0(980)|2 contribution ― |A(X(1690)|2 contribution ― Interference term contribution c 2/NDF = 188. 4/192 C. L. = 56. 4 % 26

Fit Results For J(X[1690]) = 1/2 X(1690)0 signal region Actual X(1690) signal significantly smaller (~25%) than apparent signal because of interference effects 27 27

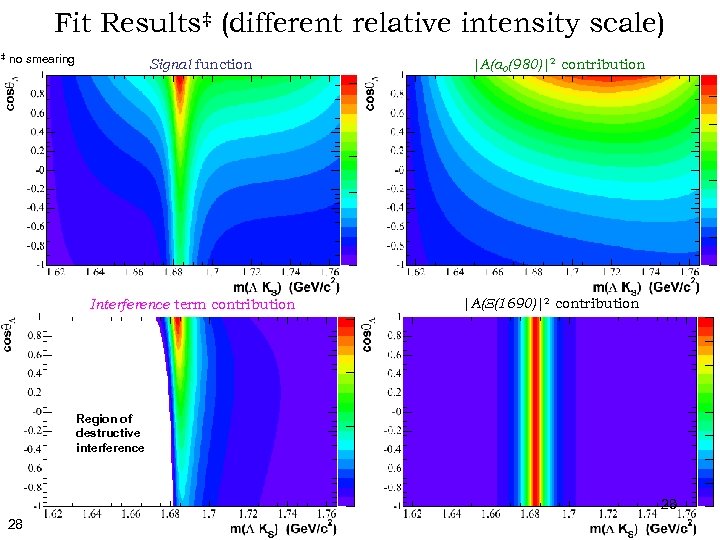
Fit Results‡ (different relative intensity scale) ‡ no smearing Signal function Interference term contribution |A(a 0(980)|2 contribution |A(X(1690)|2 contribution Region of destructive interference 28 28

X(1690)0 Spin Study Conclusions ØModel based on coherent superposition of amplitudes describing Lc+ isobar modes Ø J[X(1690)] = 1/2 favored by the data (C. L. 56. 4%) Ø J[X(1690)] = 3/2 (C. L. 1. 9%) & 5/2 (C. L. 17. 4%) yield poorer fits and systematically fail to reproduce the skewed X(1690)0 lineshape ØDiscrimination should be improved with final 29 Ba. Bar statistics

Comparison of Detector Characteristics Relevant to Cascade Physics 30

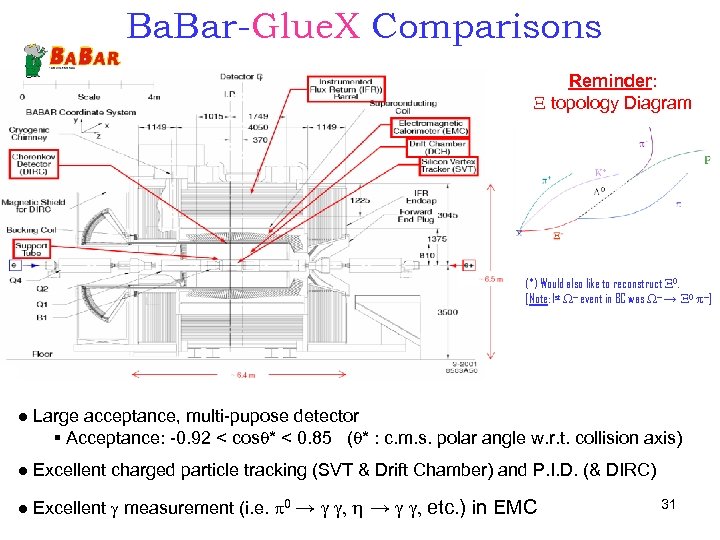
Ba. Bar-Glue. X Comparisons Reminder: X topology Diagram (*) Would also like to reconstruct X 0. [Note: 1 st W- event in BC was W- → X 0 -] ● Large acceptance, multi-pupose detector § Acceptance: -0. 92 < cosq* < 0. 85 (q* : c. m. s. polar angle w. r. t. collision axis) ● Excellent charged particle tracking (SVT & Drift Chamber) and P. I. D. (& DIRC) ● Excellent g measurement (i. e. 0 → g g, h → g g, etc. ) in EMC 31

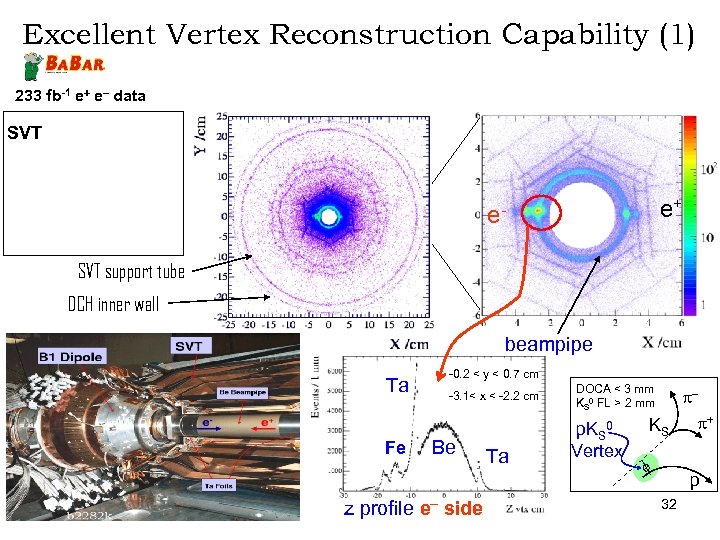
Excellent Vertex Reconstruction Capability (1) 233 fb-1 e+ e- data SVT e+ e. SVT support tube DCH inner wall beampipe Ta Fe -0. 2 < y < 0. 7 cm -3. 1< x < -2. 2 cm Be Ta DOCA < 3 mm KS 0 FL > 2 mm p. KS 0 Vertex KS + p z profile e- side 32

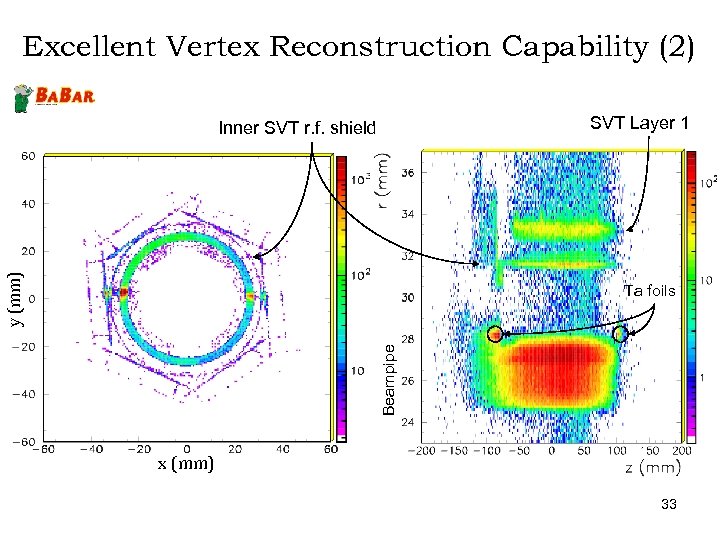
Excellent Vertex Reconstruction Capability (2) SVT Layer 1 y (mm) Inner SVT r. f. shield Beampipe Ta foils x (mm) 33

Excellent Vertex Reconstruction Capability (3) (10 mm) Radial Vertex Resolution ~ 90 mm ○ measured + fit 34

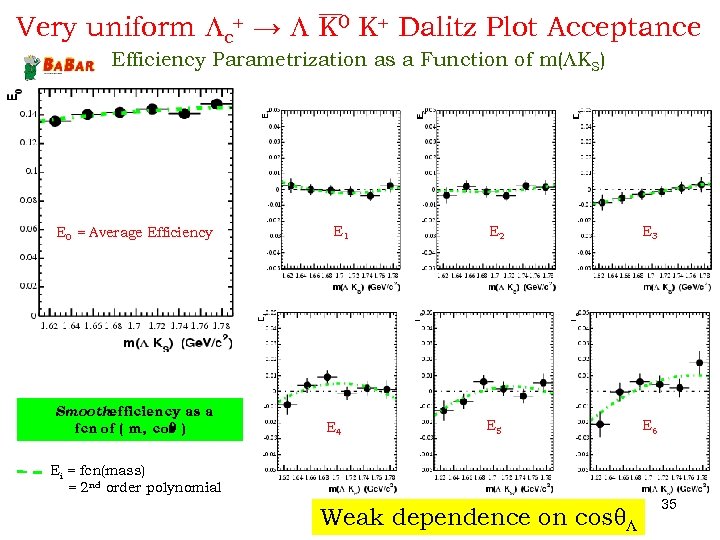
Very uniform Lc+ → L K 0 K+ Dalitz Plot Acceptance Efficiency Parametrization as a Function of m(LKS) E 0 = Average Efficiency Smoothefficiency as a fcn of ( m, cos ) q E 1 E 4 E 2 E 3 E 5 E 6 Ei = fcn(mass) = 2 nd order polynomial Weak dependence on cosq. L 35

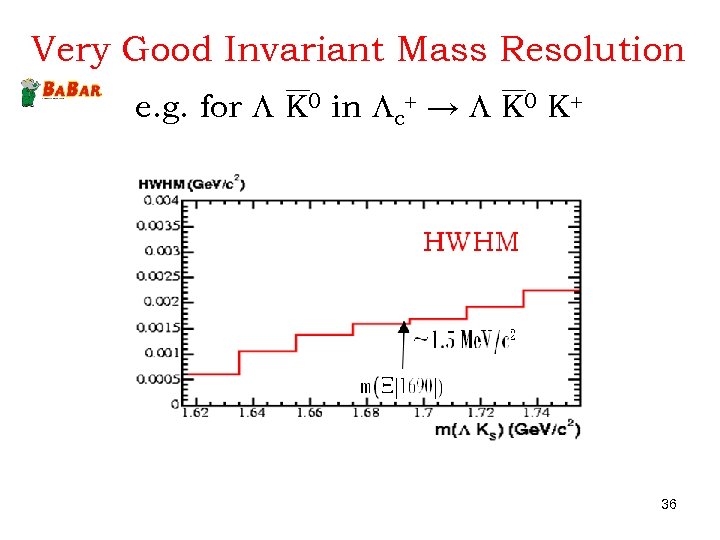
Very Good Invariant Mass Resolution e. g. for L K 0 in Lc+ → L K 0 K+ 36

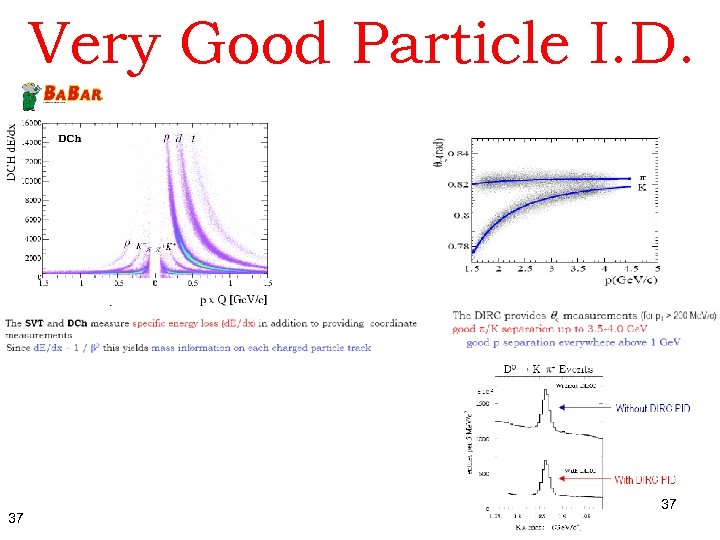
Very Good Particle I. D. 37 37

Q: How do Ba. Bar and Glue. X Compare ? Ba. Bar Yes 0. 85 > cosq* > -0. 92 • • Multiple purpose Acceptance • Charged-particle tracking Excellent Photon detection Vertex resolution Mass resolution Particle ID • • For – X Studies Glue. X Yes ~4 ; problem with polar angle charged tracks? Excellent Use Inclusive charm baryon production; high multiplicity environment select large p* events; single production mechanism; no initial polarization, etc… A: Very well Overall ! low Very good Good (? ) Very good Inclusive AND Exclusive Production; constrained kinematic fits improve substantially; multiple production mechanisms; polarization information. 38

LASS-Glue. X: A More Direct Comparison [ SLAC-R– 298, (1986) ] Innovations: K- @ 11 Ge. V/c Solenoid (2. 2 T) + Dipole (30 k. G m) ~ 4 Acceptance and Trigger Run in "Interaction Mode“ ; ~ Electronic Bubble Chamber First use of microprocessor farm in HEP : 9 370 -168 E processors built by Paul Kunz + 1 Tech. 2 3081 E processors later for MC and kinematic fitting First use of a Solenoidal Vertex magnet + detector in a fixed target experiment. 39

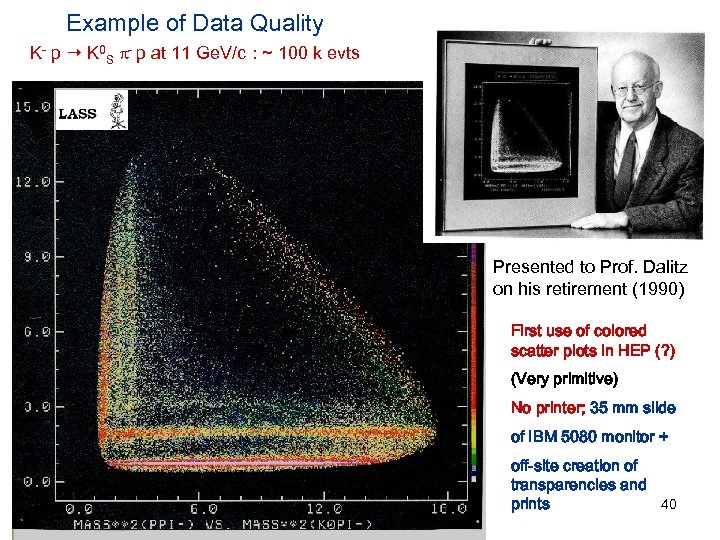
Example of Data Quality K- p K 0 S - p at 11 Ge. V/c : ~ 100 k evts Presented to Prof. Dalitz on his retirement (1990) First use of colored scatter plots in HEP (? ) (Very primitive) No printer; 35 mm slide of IBM 5080 monitor + off-site creation of transparencies and 40 prints

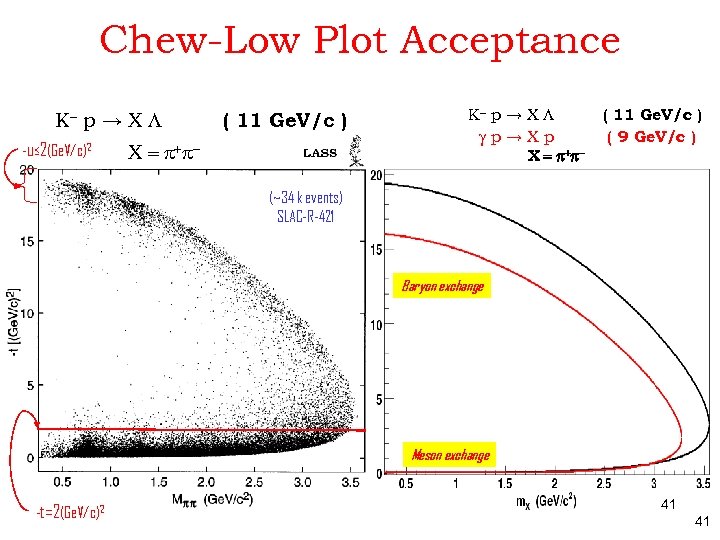
Chew-Low Plot Acceptance K- p → X L -u≤ 2(Ge. V/c)2 ( 11 Ge. V/c ) X = + - K- p → X L gp→Xp X = p+p- ( 11 Ge. V/c ) ( 9 Ge. V/c ) (~34 k events) SLAC-R-421 Baryon exchange Meson exchange -t=2(Ge. V/c)2 41 41

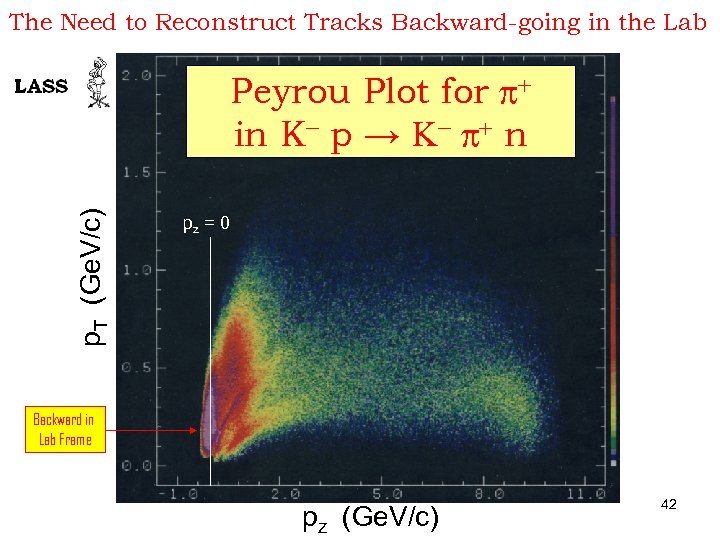
The Need to Reconstruct Tracks Backward-going in the Lab p. T (Ge. V/c) Peyrou Plot for + in K- p → K- + n pz = 0 Backward in Lab Frame pz (Ge. V/c) 42

Q: How do LASS and Glue. X Compare ? LASS • • Multiple purpose Acceptance • Charged-particle tracking spacings P. C. ’s) • • Photon detection Vertex resolution Mass resolution Particle ID For – – X Studies – 43 Glue. X [no Somewhat g detection] ~4 ; dipole covers low q Yes ~4 ; problem with polar angle charged tracks? low O. K. (2 mm wire- Very good [ 0 from missing mass] Very good Non-existent Good (? ) O. K. Very good O. K Very good Very Limited Inclusive: large flight length required (>2 cm) Exclusive: substantial gains from overall fits to topology and kinematics; multiple production mechanisms; polarization information Inclusive AND Exclusive Production; constrained kinematic fits improve substantially; multiple production mechanisms; polarization information. 43 A: Glue. X should do much better than LASS !

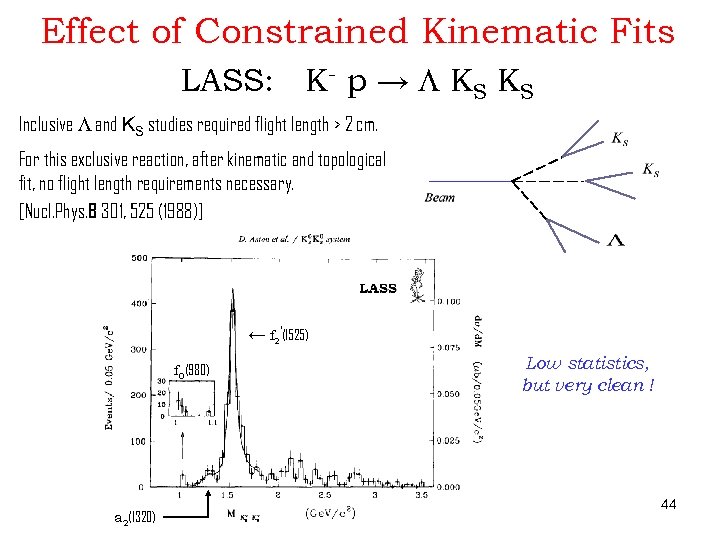
Effect of Constrained Kinematic Fits LASS: K- p → L KS KS Inclusive L and KS studies required flight length > 2 cm. For this exclusive reaction, after kinematic and topological fit, no flight length requirements necessary. [Nucl. Phys. B 301, 525 (1988)] ← f 2’(1525) f 0(980) a 2(1320) Low statistics, but very clean ! 44

Possible X Studies with Glue. X 1. Survey Processes to Provide an Overview of X(*) Photoproduction • Inclusive X- (X 0 ? ) Production – – • Feynman x and p. T 2 distributions Chew-Low plot(s) Polarization measurements Etc… Similar Studies for Cascade Resonance Production (e. g. X(1530)→X- +) and Associated Spectra – Note: In the LASS search for W*- states, the inclusive mass distribution for (X- +K-) showed nothing; however when the (X - +) was selected to correspond to the X(1530)0, a signal for the W(2250)- was observed. 45

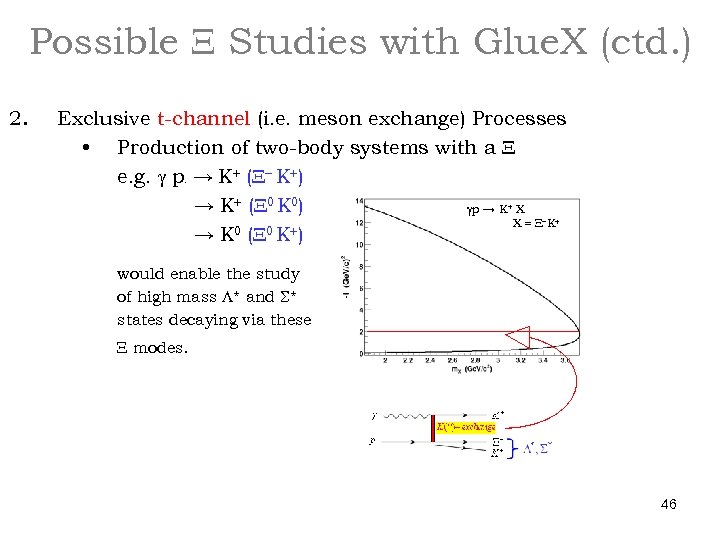
Possible X Studies with Glue. X (ctd. ) 2. Exclusive t-channel (i. e. meson exchange) Processes • Production of two-body systems with a X • e. g. g p → K+ (X- K+) • → K+ (X 0 K 0) gp → K X X=X K 0 (X 0 K+) • →K. + - • • • would enable the study of high mass L* and S* states decaying via these • + X modes. 46

Possible X Studies with Glue. X (ctd. ) • Production of three-body systems with a X, or a X* system with two-body decay: with a forward K 0: S*, L* • e. g. g p → K 0 (X- +) K+, K 0 (X 0 0) K+, K 0 (X 0 K 0) + States analyzed • → K 0 (L K 0) K+ gp → K 0 X . X = X- + K+ - can observe in a totally different context in Lc+ decay • with a forward K+: • • • e. g. g p → K+ (X- +) K 0, K+ (X- 0) K+ → K+ (X 0 -) K+, K+ (X 0 0) K 0 → K+ (L K-) K+ • • Interesting four-body possibilities when add pion • m(Lc+) e. g. g p → K+ (L K- +) K+, . . − accessible at Ba. Bar via Xc 0→ LK- +, complicated Dalitz plot 47

Possible X Studies with Glue. X (ctd. ) 3. Exclusive u-channel (i. e. baryon exchange) Processes • All of the t-channel processes discussed have corresponding uchannel counterparts in which the bachelor K+ or K 0 is attached to the proton vertex • At 9 Ge. V/c, such processes should have small cross section values; however with very large statistics and an interaction trigger, interesting results may be obtained. E. g. in LASS, the forward-produced K+K- system in K -p → L(K+K-) was studied, but when K-p →(L K-)fwd K+ was examined, a nice X(1820) signal was observed. So in g p → (X- K+)fwd K+ may see some interesting L*/S* distributions! K-p → (L K-)fwd K+ @ 11 Ge. V/c (4 c fits) ← X(1820) 48

SUMMARY 1. Three-body systems involving two-body Cascade resonance decays require analysis of the entire Dalitz plot when the statistical level is such that the shortcomings of a quasi-two-body approach become apparent. Glue. X should be in this statistical situation. 2. In terms of acceptance, track and vertex reconstruction (after kinematic fits), and particle identification capability, Glue. X should be able to perform Cascade studies of the kind suggested in section 4) provided the relevant cross section values are large enough. 49

BACKUP SLIDES 50

MIGRAD FIT PARAMETER VALUES Fit c 2/NDF = 188. 4/192 Prob. . = 56. 4% SLAC-R-868 51

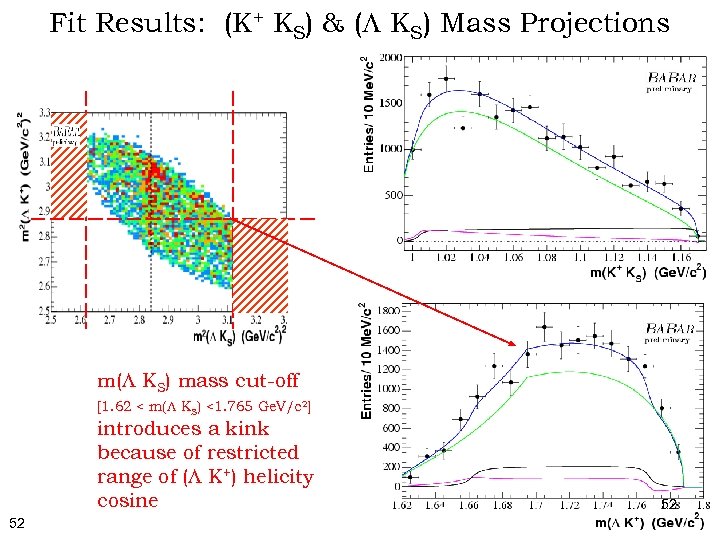
Fit Results: (K+ KS) & (L KS) Mass Projections m(L KS) mass cut-off [1. 62 < m(L KS) <1. 765 Ge. V/c 2] introduces a kink because of restricted range of (L K+) helicity cosine 52 52

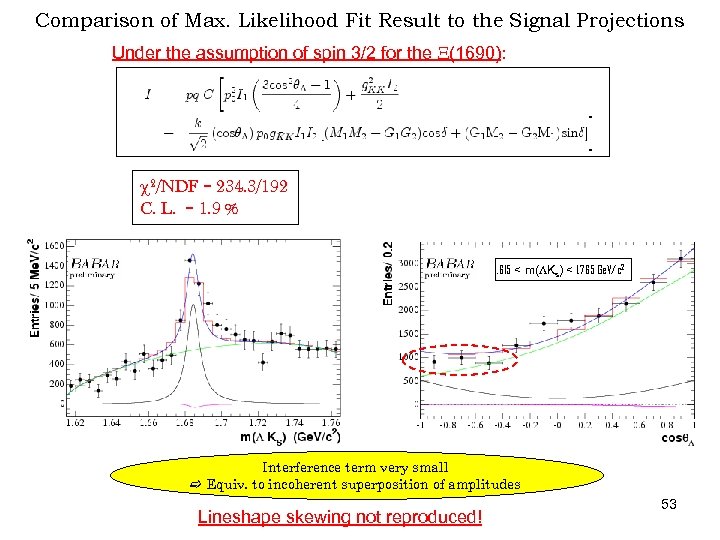
Comparison of Max. Likelihood Fit Result to the Signal Projections Under the assumption of spin 3/2 for the X(1690): c 2/NDF = 234. 3/192 C. L. = 1. 9 % 1. 615 < m(LKs) < 1. 765 Ge. V/c 2 Interference term very small Equiv. to incoherent superposition of amplitudes Lineshape skewing not reproduced! 53

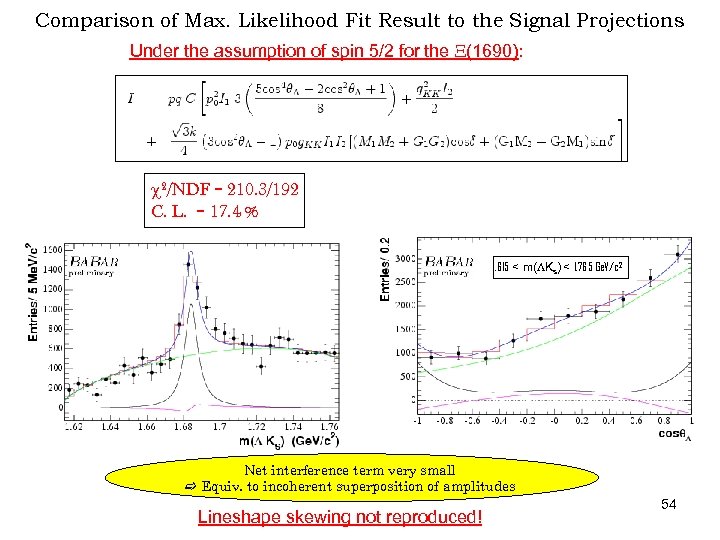
Comparison of Max. Likelihood Fit Result to the Signal Projections Under the assumption of spin 5/2 for the X(1690): c 2/NDF = 210. 3/192 C. L. = 17. 4 % 1. 615 < m(LKs) < 1. 765 Ge. V/c 2 Net interference term very small Equiv. to incoherent superposition of amplitudes Lineshape skewing not reproduced! 54

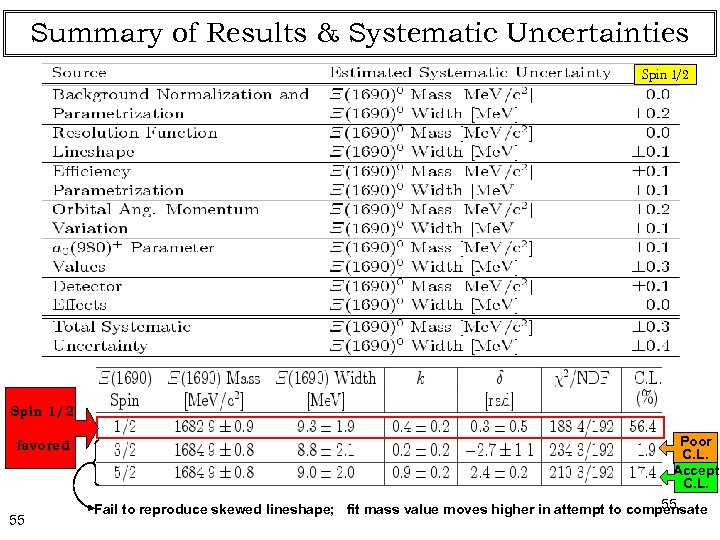
Summary of Results & Systematic Uncertainties Spin 1/2 favored 55 Poor C. L. Accept. C. L. 55 Fail to reproduce skewed lineshape; fit mass value moves higher in attempt to compensate