CARRY SAVE ADDER CSA Dima

CARRY SAVE ADDER (CSA)

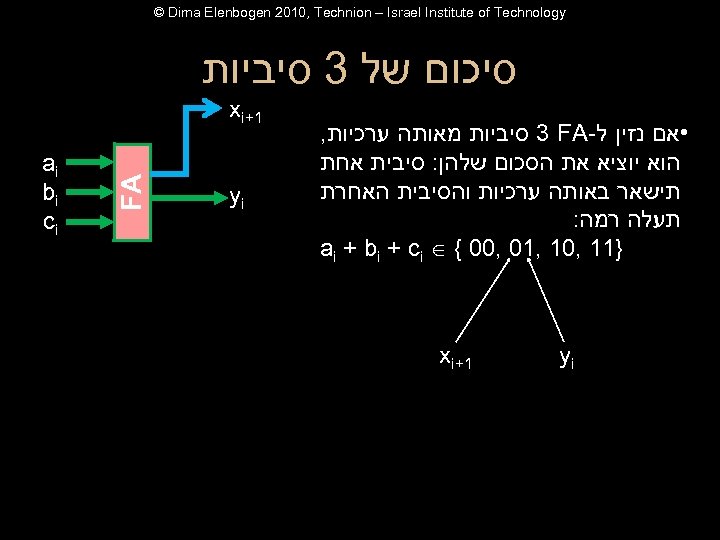© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3 סיביות yi 1+ xi yi FA • אם נזין ל- 3 FA סיביות מאותה ערכיות, הוא יוציא את הסכום שלהן: סיבית אחת תישאר באותה ערכיות והסיבית האחרת תעלה רמה: }11 , 01 , 10 , 00 { ai + bi + ci 1+ xi ai bi ci

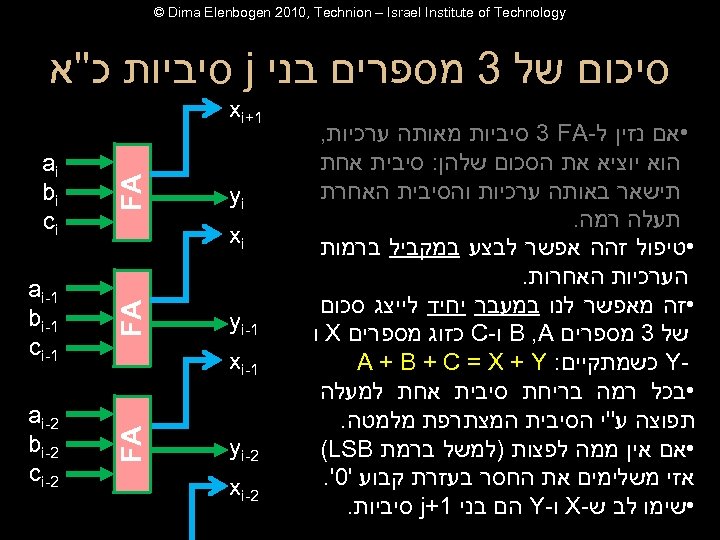© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3 מספרים בני j סיביות כ''א FA FA yi ai bi ci 1 - ai 1 - bi 1 - ci FA • אם נזין ל- 3 FA סיביות מאותה ערכיות, הוא יוציא את הסכום שלהן: סיבית אחת תישאר באותה ערכיות והסיבית האחרת תעלה רמה. • טיפול זהה אפשר לבצע במקביל ברמות הערכיות האחרות. • זה מאפשר לנו במעבר יחיד לייצג סכום של 3 מספרים B , A ו- C כזוג מספרים X ו Y כשמתקיים: A + B + C = X + Y • בכל רמה בריחת סיבית אחת למעלה תפוצה ע''י הסיבית המצתרפת מלמטה. • אם אין ממה לפצות )למשל ברמת (LSB אזי משלימים את החסר בעזרת קבוע '0'. • שימו לב ש- X ו- Y הם בני 1+ j סיביות. 1+ xi 2 - ai 2 - bi 2 - ci xi 1 - yi 1 - xi 2 - yi 2 - xi

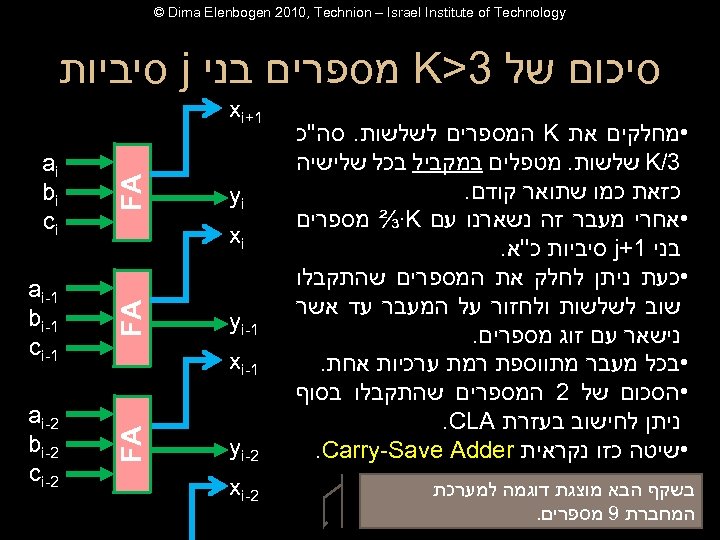© Dima Elenbogen 2010, Technion – Israel Institute of Technology סיכום של 3> K מספרים בני j סיביות FA FA בשקף הבא מוצגת דוגמה למערכת המחברת 9 מספרים. yi ai bi ci 1 - ai 1 - bi 1 - ci FA • מחלקים את K המספרים לשלשות. סה''כ 3/ K שלשות. מטפלים במקביל בכל שלישיה כזאת כמו שתואר קודם. • אחרי מעבר זה נשארנו עם ⅔∙K מספרים בני 1+ j סיביות כ''א. • כעת ניתן לחלק את המספרים שהתקבלו שוב לשלשות ולחזור על המעבר עד אשר נישאר עם זוג מספרים. • בכל מעבר מתווספת רמת ערכיות אחת. • הסכום של 2 המספרים שהתקבלו בסוף ניתן לחישוב בעזרת . CLA • שיטה כזו נקראית . Carry-Save Adder 1+ xi 2 - ai 2 - bi 2 - ci xi 1 - yi 1 - xi 2 - yi 2 - xi

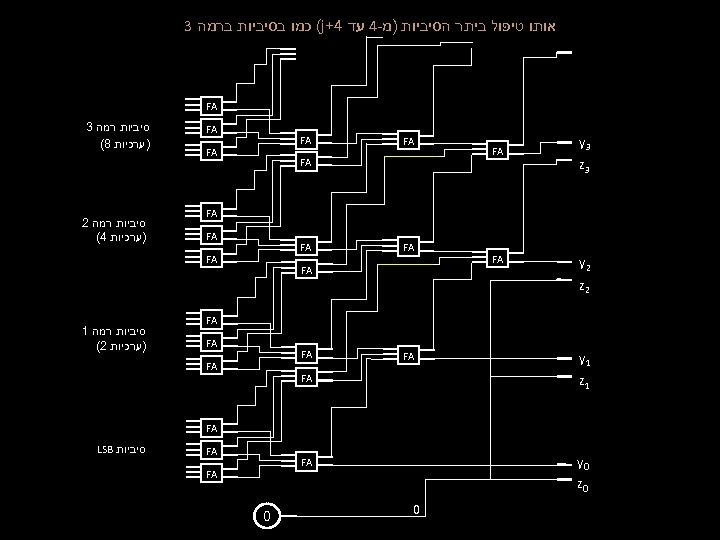אותו טיפול ביתר הסיביות )מ-4 עד 4+ (j כמו בסיביות ברמה 3 FA 3 y 3 z FA FA 2 y FA FA FA 1 z סיביות רמה 2 )ערכיות 4( סיביות רמה 1 )ערכיות 2( FA FA 0 y )ערכיות 8( FA FA 2 z סיביות רמה 3 FA FA 0 z 0 0 סיביות LSB

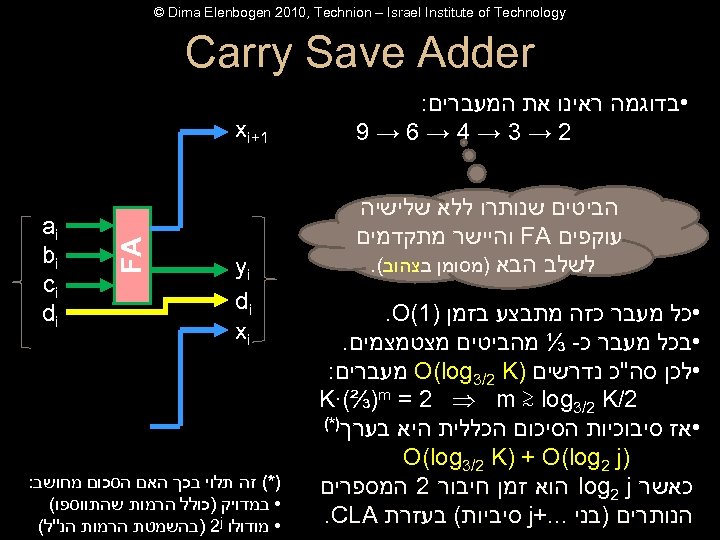© Dima Elenbogen 2010, Technion – Israel Institute of Technology Carry Save Adder • בדוגמה ראינו את המעברים: 2 → 3 → 4 → 6 → 9 • כל מעבר כזה מתבצע בזמן )1(. O • בכל מעבר כ- ⅓ מהביטים מצטמצמים. • לכן סה''כ נדרשים ) O(log 3/2 K מעברים: 2/ K∙(⅔)m = 2 m ≳ log 3/2 K • אז סיבוכיות הסיכום הכללית היא בערך)*( ) O(log 3/2 K) + O(log 2 j כאשר log 2 j הוא זמן חיבור 2 המספרים הנותרים )בני. . . + j סיביות( בעזרת . CLA yi di xi FA הביטים שנותרו ללא שלישיה עוקפים FA והיישר מתקדמים לשלב הבא )מסומן בצהוב(. 1+ xi ai bi ci di )*( זה תלוי בכך האם הסכום מחושב: • במדויק )כולל הרמות שהתווספו( • מודולו ) 2 j בהשמטת הרמות הנ''ל(

© Dima Elenbogen 2011, Technion – Israel Institute of Technology ביט j מכפל מהיר של 2 מספרים בני מחוברים j 2 סיביות כ''א j-1 בני AND מחושב בעזרת שער axby כל זוג Ø

© Dima Elenbogen 2011, Technion – Israel Institute of Technology השהיית המכפל המהיר O(log 3/2 j) + O(log 2 (2 j-1))

© Dima Elenbogen 2011, Technion – Israel Institute of Technology שאלה ממבחן עליך לתכנן מסכם carry save המסכם ביעילות j מילים של k ביטים כל אחת לרשותך הרכיבים הרגילים שהם מספר בלתי מוגבל של יחידות FA ומסכם CLA יחיד. מלבד זאת לרשותך מחוללי קבועים ומספר לא מוגבל של רכיבי סיכום של שתי מילים של 4 ביטים כל אחד המחשבים את תוצאת הסיכום ואת ה- ) carry כמתואר בשירטוט(: נניח כאן שלכל הרכיבים השהיית זמן של יחידה ושאורך המילים לסיכום ) (k גדול. בכמה זמן יתקצר זמן החישוב אם ייעשה שימוש אופטימלי ביחידות אלו? Cin 4 bit adder Cout 1 + Lat. OLD = O(log 3/2 j) + 1 = log 3/2 j + CO 1 + Lat. NEW = O(log 9/5 j) + 1 = log 9/5 j + CN

© Dima Elenbogen 2011, Technion – Israel Institute of Technology פיתרון השאלה מהמבחן Lat. OLD = log 3/2 j + CO + 1 Lat. NEW = log 9/5 j + CN + 1 Lat. OLD log 3/2 j log 2 j / log 2 3/2 log 2 9/5 Lat. NEW log 9/5 j log 2 j / log 2 9/5 log 2 3/2 lim ───── = ────── j ∞ הזמן יירד בערך פי log 2(9/5) / log 2(3/2)