Скачать презентацию Carry Look Ahead CLA Yohai Devir Скачать презентацию Carry Look Ahead CLA Yohai Devir

667ca6b3c876692a892806dd434a517e.ppt

  • Количество слайдов: 22

Carry Look Ahead (CLA) Carry Look Ahead (CLA)

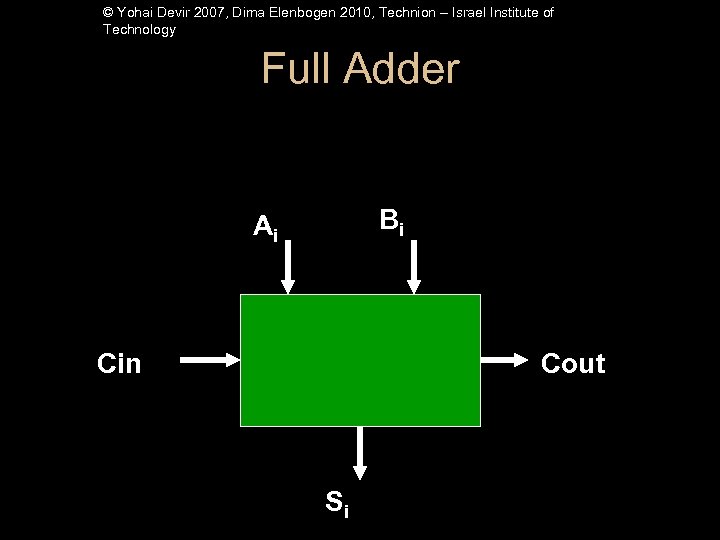© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Full © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Full Adder Bi Ai Cin Cout Si

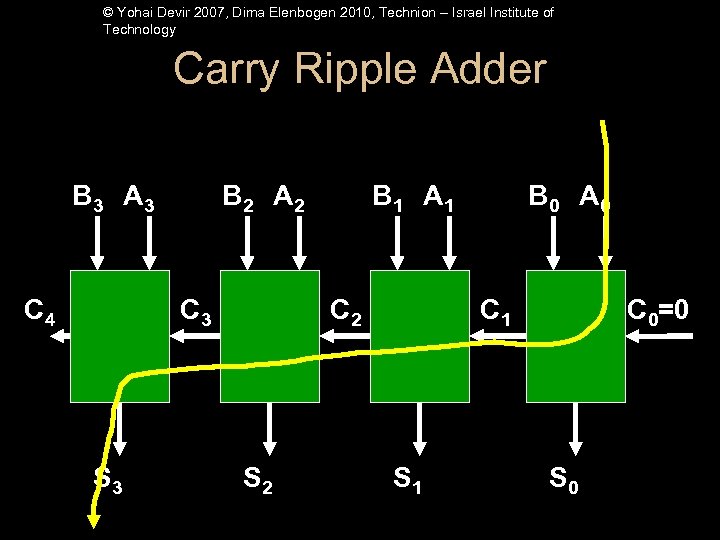© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Carry © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Carry Ripple Adder B 3 A 3 C 4 B 2 A 2 C 3 S 3 B 1 A 1 C 2 S 2 B 0 A 0 C 1 S 1 C 0=0 S 0

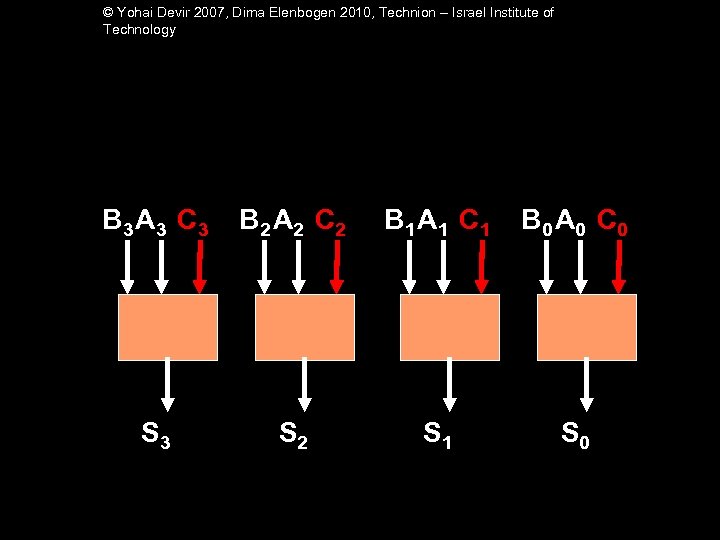© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology B © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology B 3 A 3 C 3 B 2 A 2 C 2 B 1 A 1 C 1 B 0 A 0 C 0 S 3 S 2 S 1 S 0

© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Reduction © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Reduction • Changing the goal to: Calculate the Carry vector • We can calculate S out of A, B, C in O(1) • We’d like to improve the complexity of calculating C (less than linear)

© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Three © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Three Cases 1 1 Generate: Gi ? 1 0 Propagate: Pi ? 0 ? 0 Kill Gi Pi

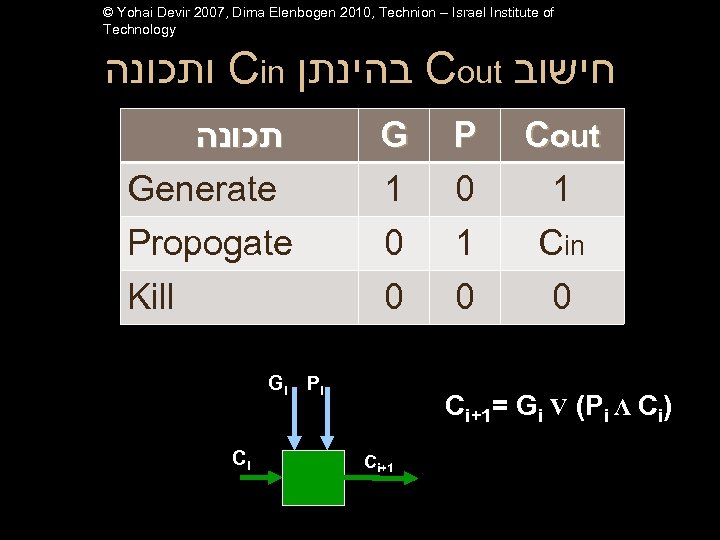© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology ותכונה © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology ותכונה Cin בהינתן Cout חישוב תכונה Generate Propogate G 1 0 P 0 1 Cout 1 Cin Kill 0 0 0 Gi Pi Ci Ci+1= Gi V (Pi Λ Ci) Ci+1

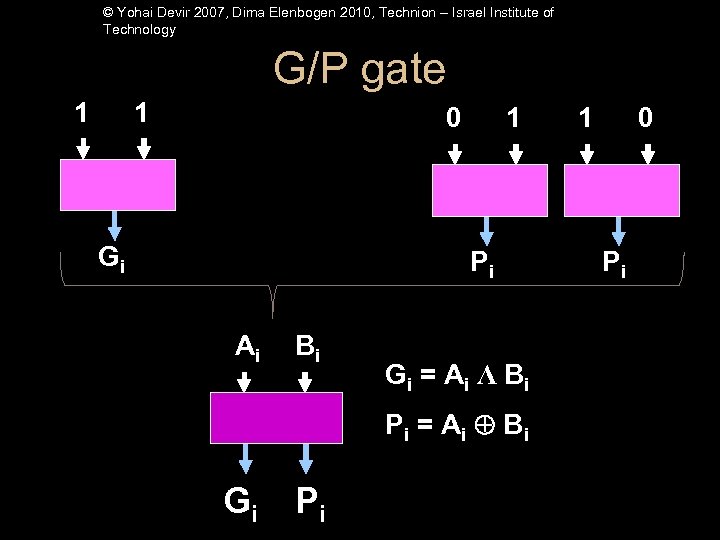© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology G/P © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology G/P gate 1 1 0 Gi 1 Pi Ai Bi G i = A i Λ Bi Pi = A i Bi Gi Pi 1 0 Pi

Calculate using 2 G/P pairs Pi+1 Pi Gi Gi+1 Ci+2=1 Gi+1 V (Gi Λ Calculate using 2 G/P pairs Pi+1 Pi Gi Gi+1 Ci+2=1 Gi+1 V (Gi Λ Pi+1) Ci Ci+1 Ci+2=Ci Pi Λ Pi+1 Ci+2=0 otherwise Gi+1 Pi+1 Gi Pi G’ = Gi+1 V (Gi Λ Pi+1) P’ = Pi Λ Pi+1 G’ P’ © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

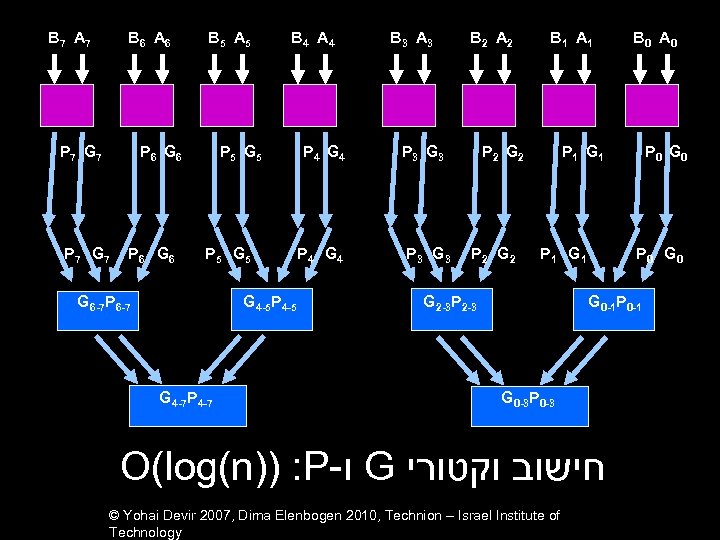B 7 A 7 B 6 A 6 P 7 G 7 B 5 B 7 A 7 B 6 A 6 P 7 G 7 B 5 A 5 P 6 G 6 P 7 G 7 P 6 G 6 B 4 A 4 P 5 G 5 G 6 -7 P 6 -7 G 4 -5 P 4 -5 G 4 -7 P 4 -7 P 4 G 4 B 3 A 3 B 2 A 2 P 3 G 3 B 1 A 1 P 2 G 2 B 0 A 0 P 1 G 1 G 2 -3 P 2 -3 P 0 G 0 G 0 -1 P 0 -1 G 0 -3 P 0 -3 O(log(n)) : P- ו G חישוב וקטורי © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

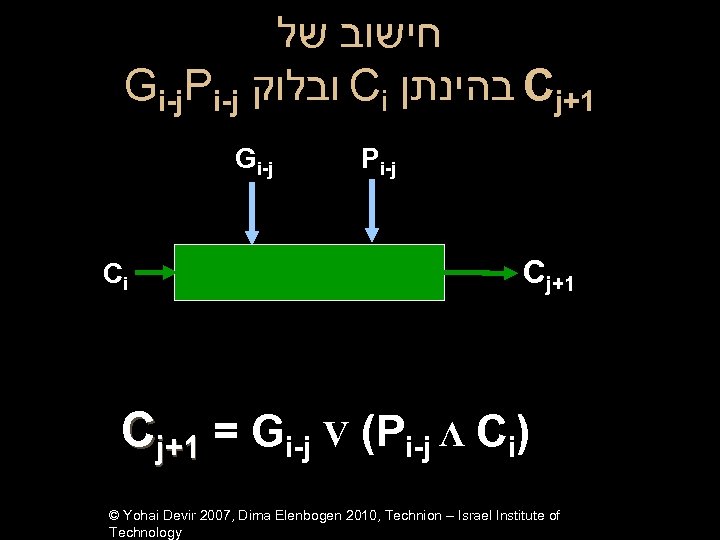חישוב של Gi-j. Pi-j ובלוק Ci בהינתן Cj+1 Gi-j Ci Pi-j Cj+1 = חישוב של Gi-j. Pi-j ובלוק Ci בהינתן Cj+1 Gi-j Ci Pi-j Cj+1 = Gi-j V (Pi-j Λ Ci) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

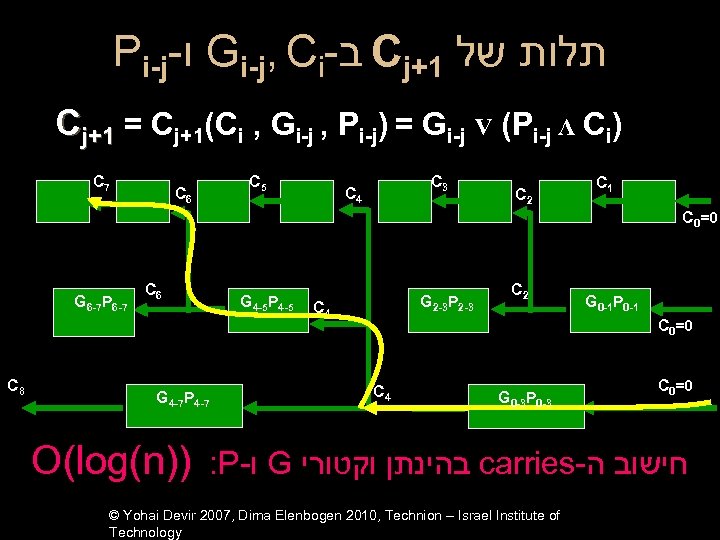Pi-j- ו Gi-j, Ci- ב Cj+1 תלות של Cj+1 = Cj+1(Ci , Gi-j , Pi-j- ו Gi-j, Ci- ב Cj+1 תלות של Cj+1 = Cj+1(Ci , Gi-j , Pi-j) = Gi-j V (Pi-j Λ Ci) C 7 C 5 C 6 C 3 C 4 C 2 C 1 C 0=0 G 6 -7 P 6 -7 C 8 C 6 G 4 -5 P 4 -5 G 4 -7 P 4 -7 O(log(n)) G 2 -3 P 2 -3 C 4 C 2 G 0 -1 P 0 -1 C 0=0 C 4 G 0 -3 P 0 -3 C 0=0 : P- ו G בהינתן וקטורי carries- חישוב ה © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

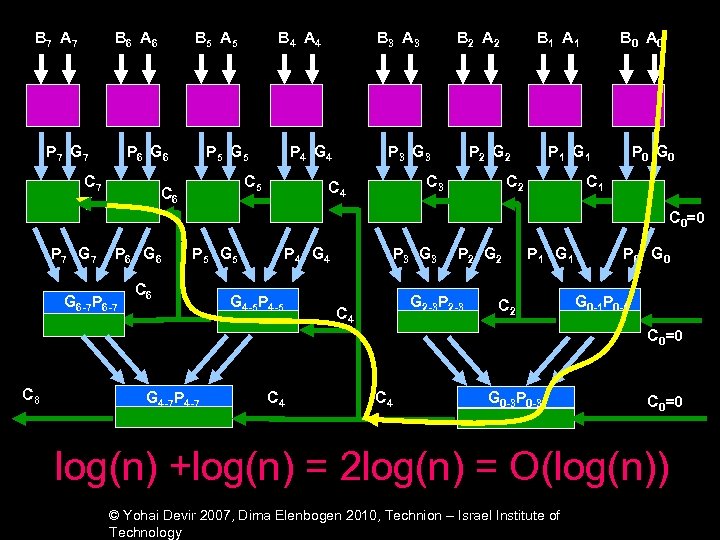B 7 A 7 B 6 A 6 P 7 G 7 B 5 B 7 A 7 B 6 A 6 P 7 G 7 B 5 A 5 P 6 G 6 C 7 B 4 A 4 P 5 G 5 P 4 G 4 C 5 C 6 B 3 A 3 B 2 A 2 P 3 G 3 P 2 G 2 C 3 C 4 B 1 A 1 B 0 A 0 P 1 G 1 C 2 P 0 G 0 C 1 C 0=0 P 7 G 7 P 6 G 6 -7 P 6 -7 P 5 G 5 C 6 P 4 G 4 -5 P 4 -5 P 3 G 3 P 2 G 2 -3 P 2 -3 C 4 P 1 G 1 C 2 P 0 G 0 -1 P 0 -1 C 0=0 C 8 G 4 -7 P 4 -7 C 4 G 0 -3 P 0 -3 C 0=0 log(n) +log(n) = 2 log(n) = O(log(n)) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

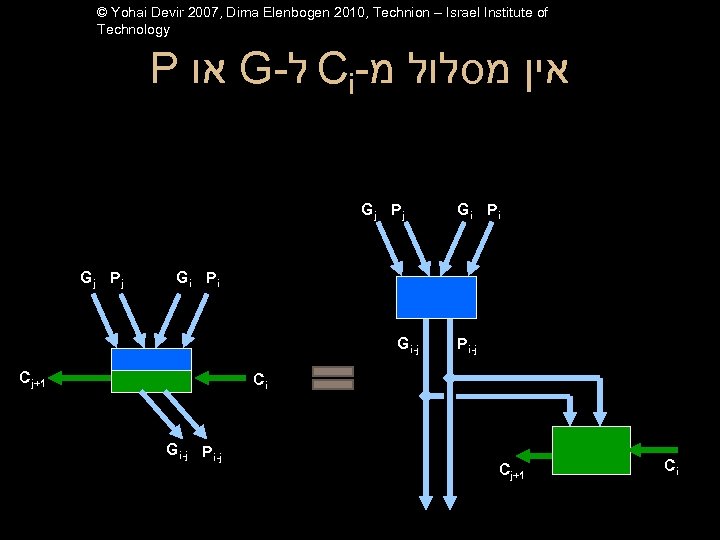© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology P © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology P או G- ל Ci- אין מסלול מ Gj Pj Gi Pi G 0 -1 P 0 -1 Gi-j G 0 -1 P 0 -1 Cj+1 Gi Pi Pi-j Ci Gi-j Pi-j Cj+1 Ci

Timeline of Calculations for n=8 C 0 is 0 from the beginning. Ai Bi Timeline of Calculations for n=8 C 0 is 0 from the beginning. Ai Bi 1) Gi. Pi for each 0 ≤ i < 8 2) C 1 (by C 0 and G 0 P 0) Gi Pi G 0 -1 P 0 -1, G 2 -3 P 2 -3, G 4 -5 P 4 -5, G 6 -7 P 6 -7 4) C 3 (by C 2 and G 2 P 2) 3) C 2 (by C 0 and G 0 -1 P 0 -1) C 4 (by C 0 and G 0 -3 P 0 -3) G 0 -3 P 0 -3, G 4 -7 P 4 -7 5) C 5 (by C 4 and G 4 P 4) // Now all G. . . P. . . are known C 6 (by C 4 and G 4 -5 P 4 -5) 6) C 7 (by C 6 and G 6 P 6) © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology

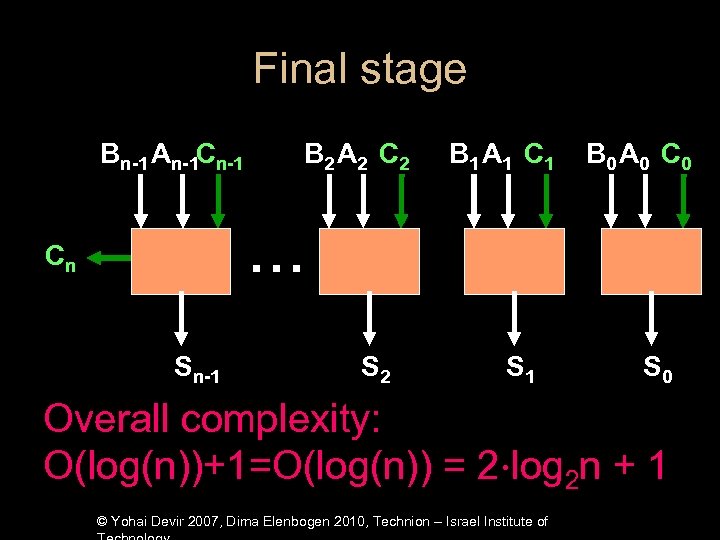Final stage Bn-1 An-1 Cn-1 B 2 A 2 C 2 B 1 A Final stage Bn-1 An-1 Cn-1 B 2 A 2 C 2 B 1 A 1 C 1 B 0 A 0 C 0 . . . Cn Sn-1 S 2 S 1 S 0 Overall complexity: O(log(n))+1=O(log(n)) = 2⋅log 2 n + 1 © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of

Example 2 from. pdf No! Adder Calculation Time Ripple-Carry n Carry-Look-Ahead 2∙log 2 n Example 2 from. pdf No! Adder Calculation Time Ripple-Carry n Carry-Look-Ahead 2∙log 2 n + 1 CLA is better when: 2∙log 2 n + 1 < n n≥ 6 © Dima Elenbogen 2010, Technion – Israel Institute of Technology

© Yohai Devir 2007, Dima Elenbogen 2011, Technion – Israel Institute of Technology 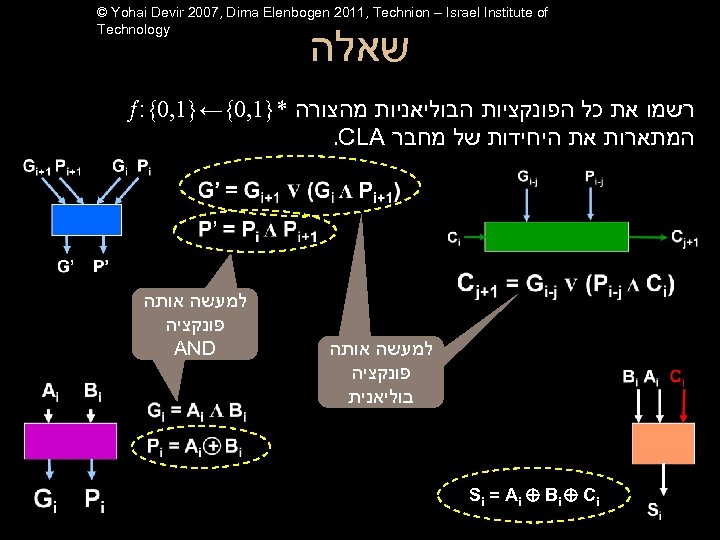© Yohai Devir 2007, Dima Elenbogen 2011, Technion – Israel Institute of Technology שאלה רשמו את כל הפונקציות הבוליאניות מהצורה *}1, 0{←}1, 0{: המתארות את היחידות של מחבר . CLA למעשה אותה פונקציה בוליאנית AND Si = A i Bi Ci למעשה אותה פונקציה AND

© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Example © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Example 3 from. pdf Pi+2 Ci+3 Gi+2 Pi+1 Ci+2 Gi+1 Pi Gi Ci+1 Ci G* = Gi+2 + Gi+1 Pi+2 + Gi. Pi+1 Pi+2 P* = Pi Pi+1 Pi+2

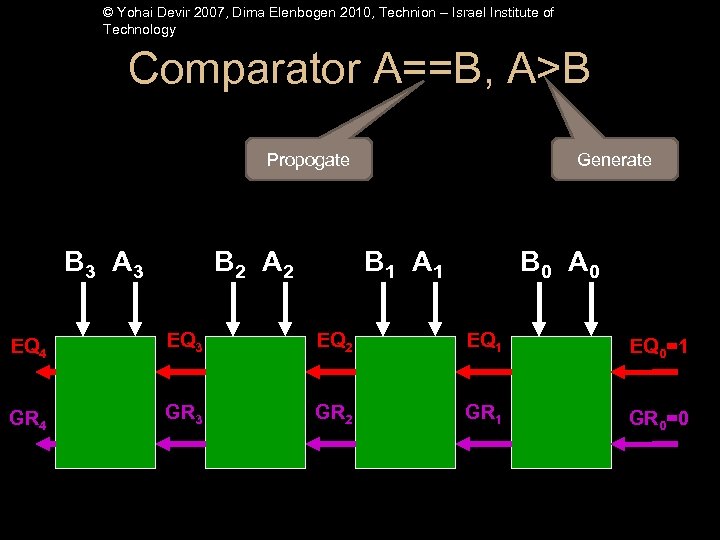© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Comparator © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Comparator A==B, A>B Propogate B 3 A 3 B 2 A 2 Generate B 1 A 1 B 0 A 0 EQ 4 EQ 3 EQ 2 EQ 1 EQ 0=1 GR 4 GR 3 GR 2 GR 1 GR 0=0

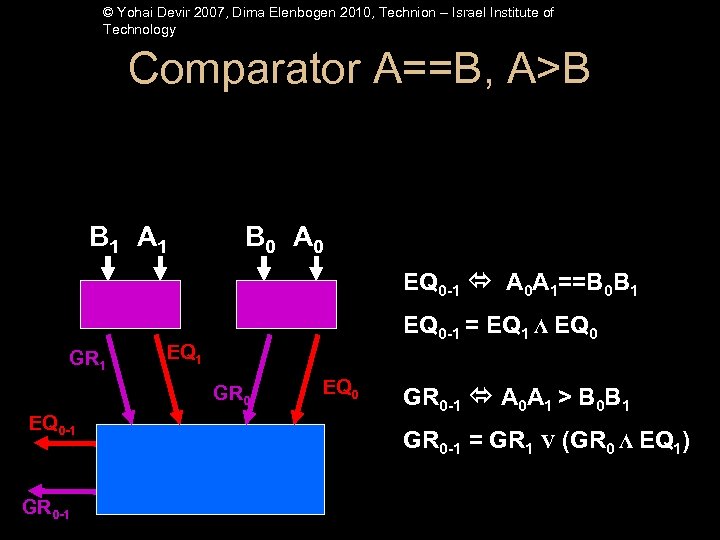© Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Comparator © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology Comparator A==B, A>B B 1 A 1 B 0 A 0 EQ 0 -1 A 0 A 1==B 0 B 1 GR 1 EQ 0 -1 = EQ 1 Λ EQ 0 EQ 1 GR 0 EQ 0 -1 GR 0 -1 EQ 0 GR 0 -1 A 0 A 1 > B 0 B 1 GR 0 -1 = GR 1 V (GR 0 Λ EQ 1)

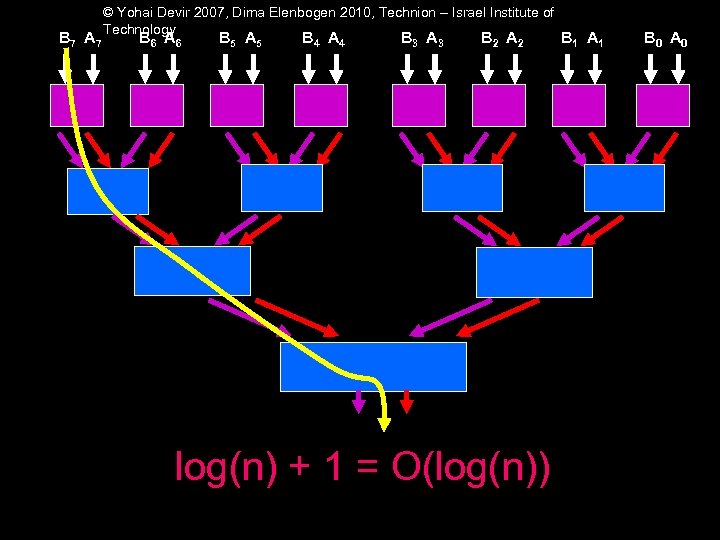B 7 A 7 © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel B 7 A 7 © Yohai Devir 2007, Dima Elenbogen 2010, Technion – Israel Institute of Technology B 6 A 6 B 5 A 5 B 4 A 4 B 3 A 3 B 2 A 2 log(n) + 1 = O(log(n)) B 1 A 1 B 0 A 0