4d370526ba8ae872da156e19a41a93fa.ppt
- Количество слайдов: 21

Can we quantify controls of snowalbedo feedback using satellitebased snow & albedo estimations? Hongxu Zhao and Richard Fernandes Canada Centre for Remote Sensing

Outline Part 1: • Motivation & Hall et al’s work • A new snow cover dataset Part 2: • Quantifying Snow-albedo feedback(SAF) • Summary
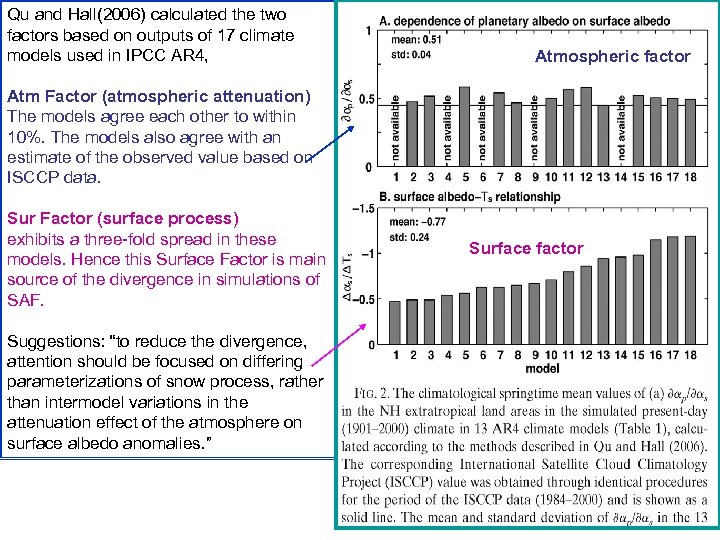
Qu and Hall(2006) calculated the two Snow albedo feedback (SAF) factors based on outputs of 17 climate models used in IPCC AR 4, Atmospheric factor Atm Factor (atmospheric attenuation) Following Qu and Hall (2006, 2007), and Cess and Potter (1988), the The models agree SAF can be determined by the product of two terms, one strength of each other to within 10%. The models also agree with an of planetary albedo on surface albedo and the representing the dependence estimate of the observed valuechangeon surface albedo induced by a unit surface other representing the based in ISCCP data. air temperature change. Sur Factor (surface process) exhibits a three-fold spread in these models. Hence this Surface Factor is main source of the divergence in simulations of SAF. Atmosp surface Surface factor Suggestions: “to reduce the divergence, Where Q (constant) and Qnet are the incoming and net shortwave attention should be focused on differing radiation snow process, rather parameterizations ofat TOA, αs is the surface albedo, and αp is the planetary albedo. than intermodel variations in the attenuation effect of the atmosphere on surface albedo anomalies. ”
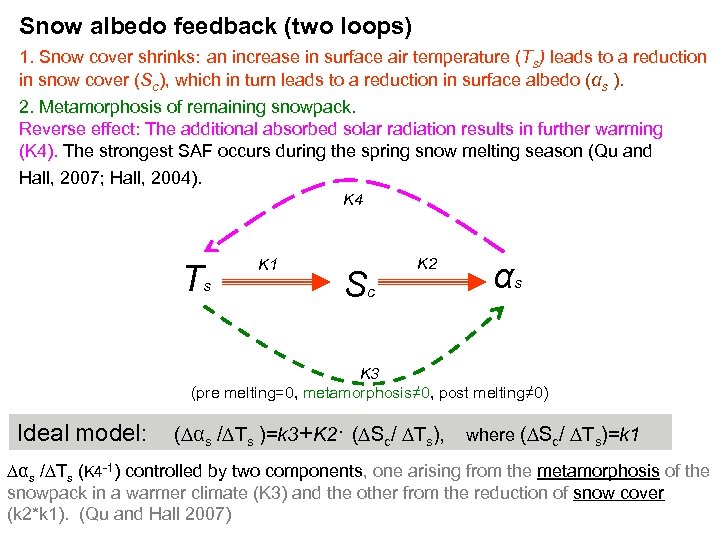
Snow albedo feedback (two loops) 1. Snow cover shrinks: an increase in surface air temperature (Ts) leads to a reduction in snow cover (Sc), which in turn leads to a reduction in surface albedo (αs ). 2. Metamorphosis of remaining snowpack. Reverse effect: The additional absorbed solar radiation results in further warming (K 4). The strongest SAF occurs during the spring snow melting season (Qu and Hall, 2007; Hall, 2004). K 4 Ts K 1 Sc K 2 αs K 3 (pre melting=0, metamorphosis≠ 0, post melting≠ 0) Ideal model: (∆αs /∆Ts )=k 3+K 2· (∆Sc/ ∆Ts), where (∆Sc/ ∆Ts)=k 1 ∆αs /∆Ts (K 4 -1) controlled by two components, one arising from the metamorphosis of the snowpack in a warmer climate (K 3) and the other from the reduction of snow cover (k 2*k 1). (Qu and Hall 2007)
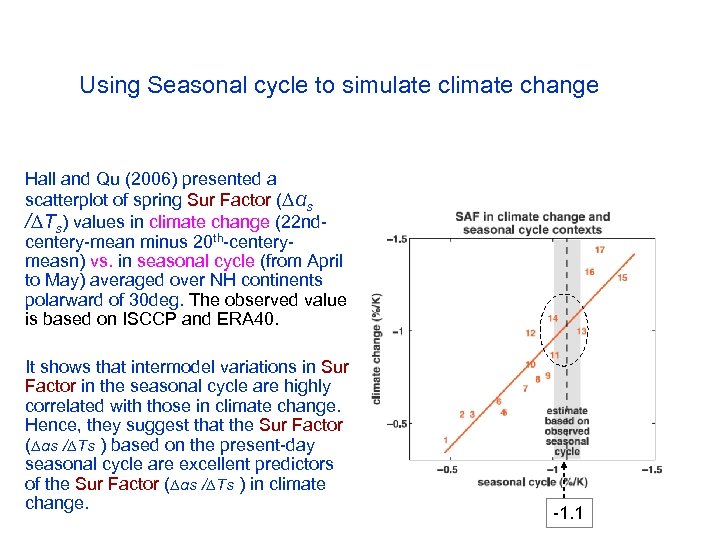
Using Seasonal cycle to simulate climate change Hall and Qu (2006) presented a scatterplot of spring Sur Factor (∆αs /∆Ts) values in climate change (22 ndcentery-mean minus 20 th-centerymeasn) vs. in seasonal cycle (from April to May) averaged over NH continents polarward of 30 deg. The observed value is based on ISCCP and ERA 40. It shows that intermodel variations in Sur Factor in the seasonal cycle are highly correlated with those in climate change. Hence, they suggest that the Sur Factor (∆αs /∆Ts ) based on the present-day seasonal cycle are excellent predictors of the Sur Factor (∆αs /∆Ts ) in climate change. -1. 1

A Daily 5 km snow cover product extracted from AVHRR Polar Pathfinder (APP) data (APP snow) Current in-situ snow cover datasets have limited spatial coverage while satellitebased snow cover records have either limited historical extent (e. g. MODIS) or limited temporal and spatial resolution (e. g. , NOAA weekly snow cover, Robinson) constrained by clouds, specific sensor availability, or processing methodology. Based on a new CCRS snow mapping algorithm, we have produced the new daily 5 km APP snow cover (Zhao and Fernandes, 2009 JGR in press), including during cloudy conditions, over Northern Hemisphere land surfaces over 1982 -2004. The APP snow cover maps showed an 85% agreement rate or better at 95% of the in-situ sites (at a comparable level of agreement to in-situ snow cover for MODIS 0. 05 degree snow cover estimates). The almost continuous spatial and temporal coverage ability of the APP snow product will benefit estimation of spring snowmelt dates and snow-albedo feedback over northern circumpolar regions. Wang and Key (2005) developed all sky APP extended daily 25 km albedo product over the period of time. The snow cover (subsampled to 25 km) was recalculated into snow fraction based on an approximate 2. 5 degree grid cell box while the albedo is simply averaged over the same 2. 5 degree grid cell box to match the ERA 40 air temperature spatial resolution. Finally, the daily data was averaged to obtain monthly mean fields.

Almost continuous spatial coverage of the APP snow maps White=snow; Green=land; Black=not available; Blue=water. Figure 1. Snow cover maps of (a) APP and (b) MODIS on 30 April 2002. Note that white color indicates snow cover, green indicates snow free land, black indicates missing or no data, and blue indicates water bodies or outside the APP domain.
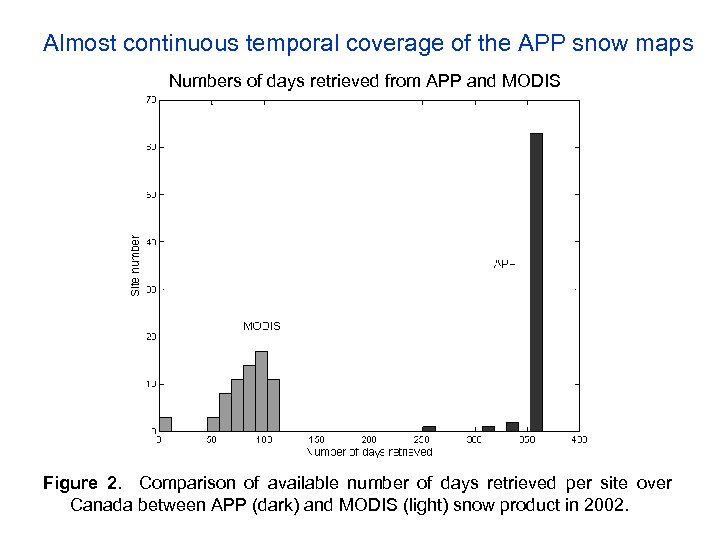
Almost continuous temporal coverage of the APP snow maps Numbers of days retrieved from APP and MODIS Figure 2. Comparison of available number of days retrieved per site over Canada between APP (dark) and MODIS (light) snow product in 2002.
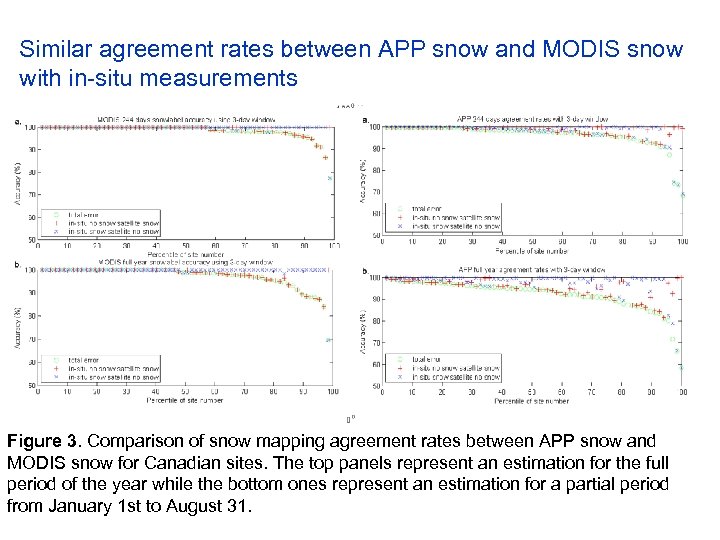
Similar agreement rates between APP snow and MODIS snow with in-situ measurements Figure 3. Comparison of snow mapping agreement rates between APP snow and In-situ sites over Canada & Eurasia MODIS snow for Canadian sites. The top panels represent an estimation for the full period of the year while the bottom ones represent an estimation for a partial period from January 1 st to August 31.

Snowmelt dates based on the APP snow Figure 4. Spatial distribution of the mean snowmelt dates (unit: DOY) over Northern Hemisphere, presented (a) by 20 DOY interval (b) continuously but focusing on high latitudes. The value of 250 (white color) is assigned to permanent snow.
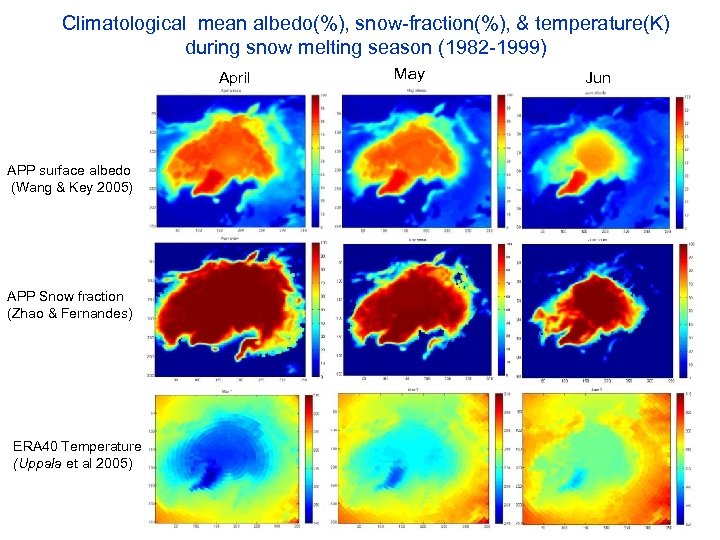
Climatological mean albedo(%), snow-fraction(%), & temperature(K) during snow melting season (1982 -1999) April APP surface albedo (Wang & Key 2005) APP Snow fraction (Zhao & Fernandes) ERA 40 Temperature (Uppala et al 2005) May Jun
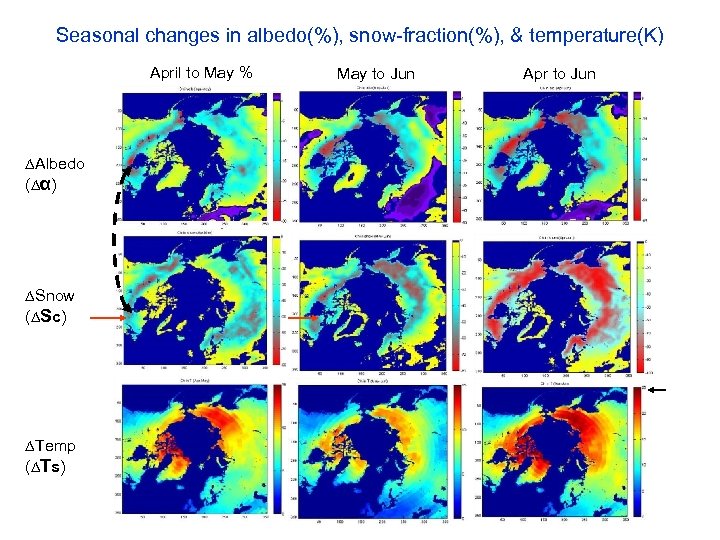
Seasonal changes in albedo(%), snow-fraction(%), & temperature(K) April to May % ∆Albedo (∆α) ∆Snow (∆Sc) ∆Temp (∆Ts) May to Jun Apr to Jun
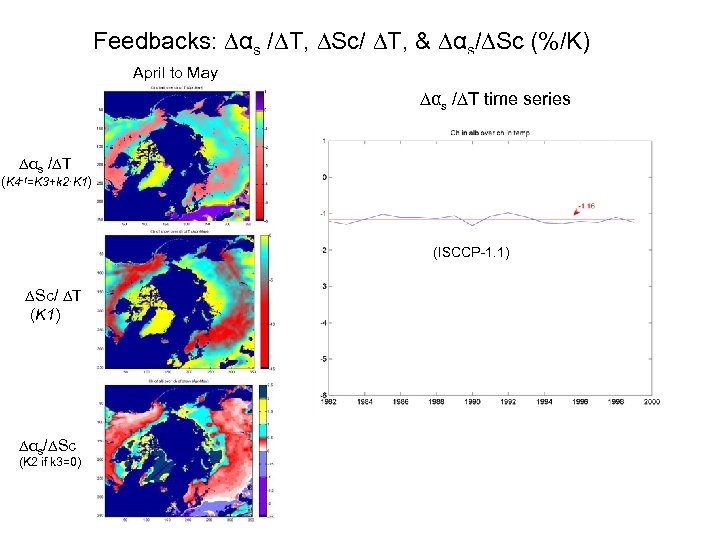
Feedbacks: ∆αs /∆T, ∆Sc/ ∆T, & ∆αs/∆Sc (%/K) April to May to Jun Apr to Jun ∆αs /∆T time series ∆αs /∆T (K 4 -1=K 3+k 2·K 1) (ISCCP-1. 1) ∆Sc/ ∆T (K 1) ∆αs/∆Sc (K 2 if k 3=0)

Approach 1: linear regression Using the method of Ordinary Least Squares, the regression line that minimizes the sum of the squares of errors can be found based on the 1982~1999 satellite observations. (∆αs /∆Ts)=k 3+K 2·(∆Sc/ ∆Ts) y=a+b · x Robust regression was suggested by Fernandes and Leblanc (2005) when dealing with remote sensing data that are not normally random distributions, say, with outliers.
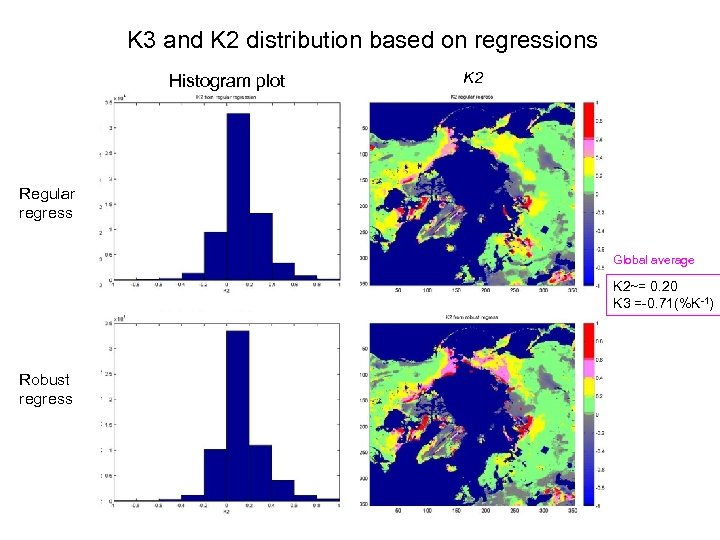
K 3 and K 2 distribution based on regressions K 3 Histogram plot K 2 Regular regress Global average K 2~= 0. 20 K 3 =-0. 71(%K-1) Robust regress
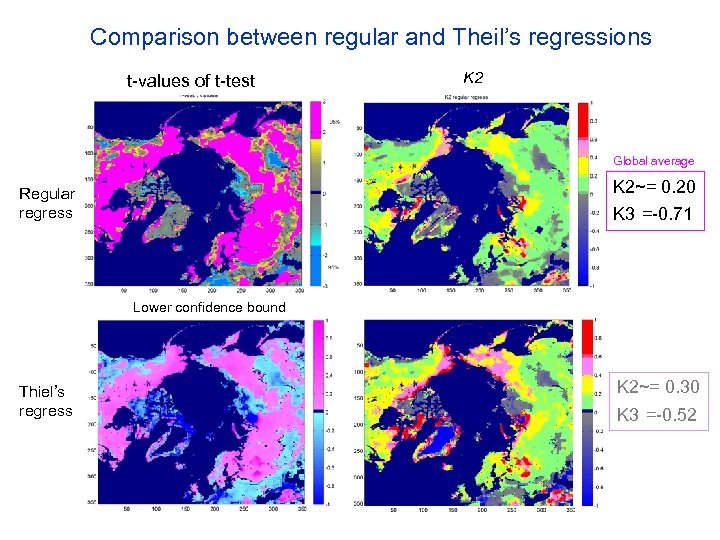
Comparison between regular and Theil’s regressions K 3 t-values of t-test K 2 Global average K 2~= 0. 20 Regular regress K 3 =-0. 71 Lower confidence bound Thiel’s regress K 2~= 0. 30 K 3 =-0. 52

Approach 2: an approximation Qu and Hall (06) developed an approximation method to calculate K 2 and K 3: K 2=1/2·(αfsnow + αpsnow )- αland K 3=1/2·(Sfc+Spc)·(αfsnow - αpsnow )/ ∆Ts - αland Where, the superscripts “f” and “p” represent the future and present climate; Snow-free land albedo αland is defined as mean albedo from snowmelt end date to 10 days after; effective snow albedo (completely snow-covered surface) αisnow ={ αis -(1 -Sic) αland}/Sic; Sc represents snow cover fraction. K 2: the mean contrast between effective snow albedo and snow free land albedo. K 3: changes in effective snow albedo with respect to changes in Ts, modulated by mean snow cover.
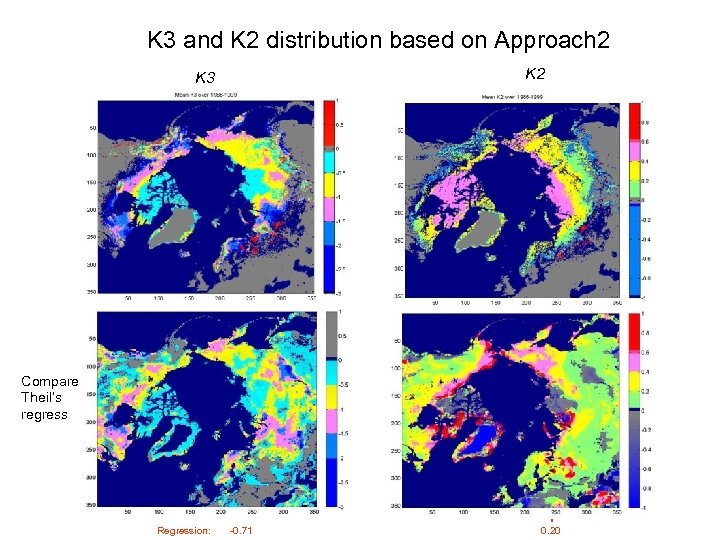
K 3 and K 2 distribution based on Approach 2 K 3 Compare Theil’s regress Median=-0. 77 Regression: K 2~=0. 30 -0. 71 0. 20
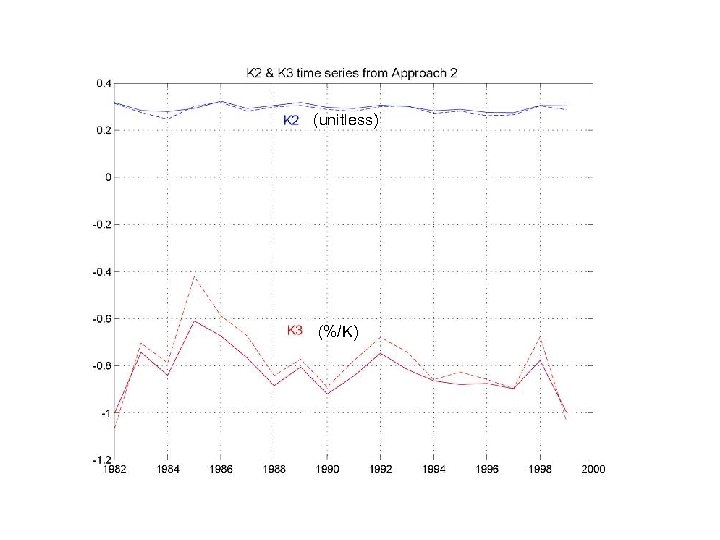
(unitless) (%/K)
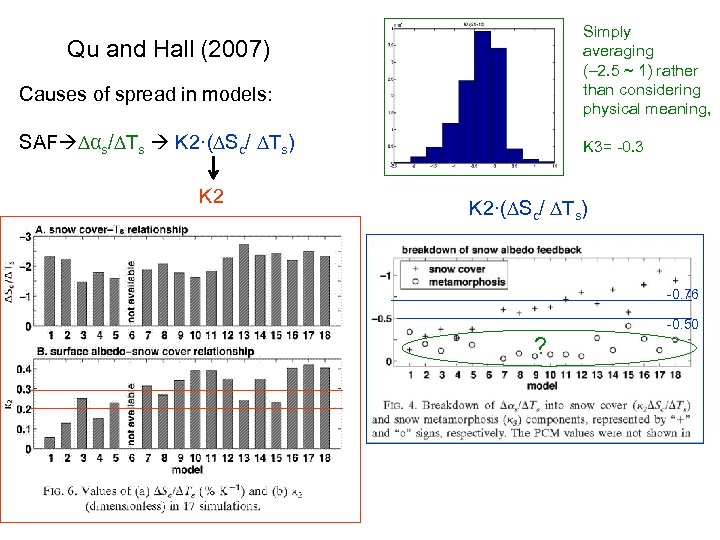
Simply averaging (– 2. 5 ~ 1) rather than considering physical meaning, Qu and Hall (2007) Causes of spread in models: SAF ∆αs/∆Ts K 2·(∆Sc/ ∆Ts) K 2 K 3= -0. 3 K 2·(∆Sc/ ∆Ts) -0. 76 -0. 50 ?

Summary • Based on the APP snow and albedo datasets, we can obtain circumpolar quantities of the snow-albedo feedback parameters, and the global average magnitude ∆αs /∆Ts is – 1. 16 ± 0. 06 comparable to Qu and Hall ISCCP’s value (-1. 1). • k 2 (0. 2~0. 3) is within the range of models’ spread (Qu and Hall, 2006). K 2 is of large-scale spatial characteristics, stable for multiple years. • K 3 (-0. 5~-0. 7) is not uniformly distributed and has an apparent regional characteristics and interannual variability.
4d370526ba8ae872da156e19a41a93fa.ppt