Callable Bonds Professor Anh Le 0

Callable Bonds Professor Anh Le

0 – Plan 1. 2. 3. 4. 5. 6. 7. 8. Callable bonds – what and why? Yields to call, worst Valuation Spread due to optionality Z-spread Option-adjusted spread Callable prices and interest rates Duration and convexity

1 – Callable bonds – what? • Bonds that give issuer the option to call home (prepay) the bonds at some price (call price) • Many bonds, call price = par value Example: Fixed rate mortgages • Many, call price = par value + premium and then declines over time

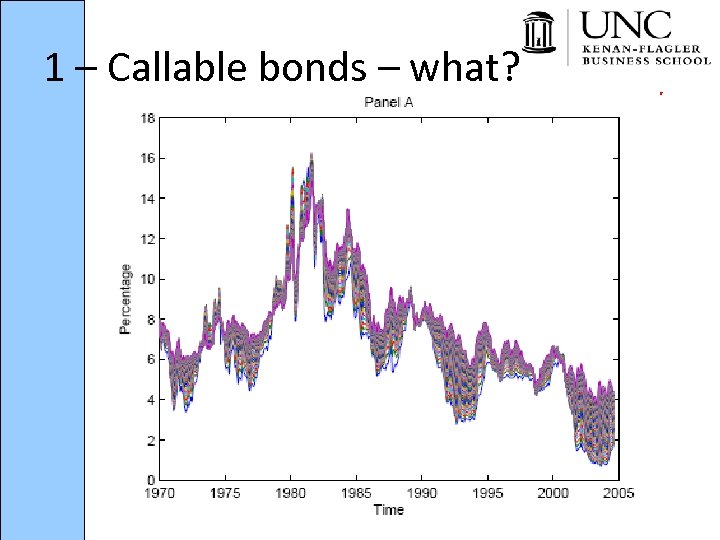
1 – Callable bonds – what?

1 – Callable bonds – what? Example: 2 -yr, $100 face, 8%-coupon callable at time 1 at a call price of $100. What happens if: – The actual price of the bond at time 1 is $105? – The actual price of the bond at time 1 is $95?

1 – Callable bonds – what? • Callable bonds are not attractive to lenders since they can be called at very bad times. • To make the bonds more attractive, some bonds have call protection period. – Example: a typical structure is “ 10 -year noncall 5” meaning the bond has a stated maturity of 10 years and is not callable for the first 5 years

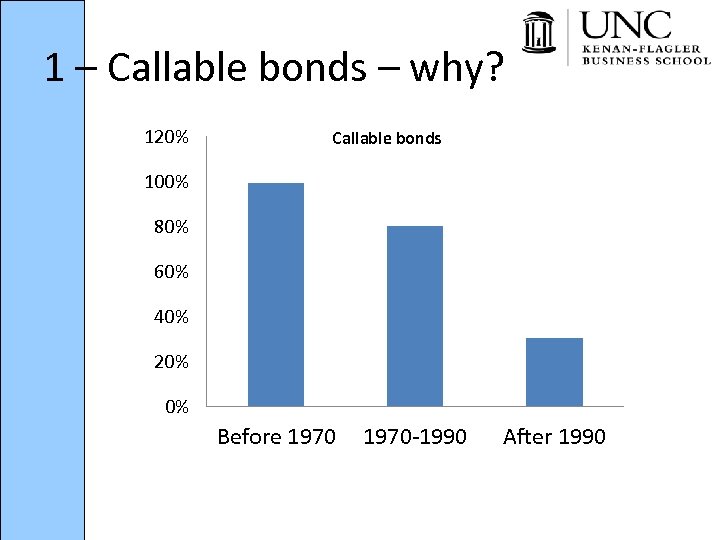
1 – Callable bonds – why? 120% Callable bonds 100% 80% 60% 40% 20% 0% Before 1970 -1990 After 1990

1 – Callable bonds – why? Hedging • Callable bonds allow issuers to refinance their high-coupon-paying bonds by cheaper bonds a means of hedging against future interest rate decreases • When is hedging most needed? How can we reconcile this with the decline in callable bonds issuance after 1990?

1 – Callable bonds – why? Signaling • If firms issue non-callable bonds and lock in a fixed rate, they can only benefit if firms become worse in credit quality • If firms issue callable bonds they may be hinting that they are confident about the prospect that their credit quality might improve in the future

2 – Yields to maturity, call, worst • Bond traders like yields • Callable bonds don’t have fixed cash flows: – Yields-to-maturity: assuming that the bond will be held until maturity for sure – Yields-to-call: assuming that the bond will be called for sure – Yields-to-worst: the smaller of the above two

2 – Yields to maturity, call, worst • Example: 2 -yr, $100 face, 8%-coupon callable at time 1 at a call price of $100. The bond is selling for $99.

2 – Yields to maturity, call, worst • Suppose:

2 – Yields to maturity, call, worst • The 2 -yr callable (c=8%): $99 • The 1 -yr non-callable (c=8%): $100 • The 2 -yr non-callable (c=8%): $98 • Do these prices look right?

2 – Yields to maturity, call, worst • When firm issues a 2 -year bond callable at time 1: 1. The firm issues a 2 -year non-callable bond but they have the option to buy the bond back at t=1 for a call price of $100; OR 2. The firm issues a 1 -year non-callable bond but they have the option to extend the maturity of the bond to 2 years at time t = 1.

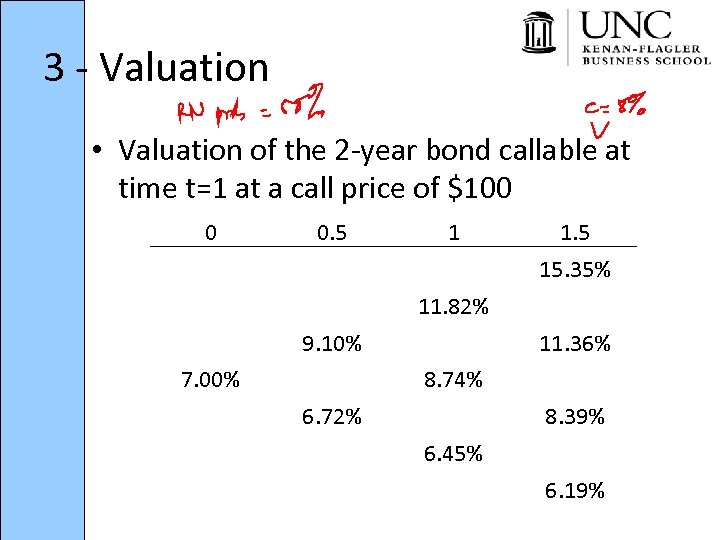
3 - Valuation • Valuation of the 2 -year bond callable at time t=1 at a call price of $100 0 0. 5 1 1. 5 15. 35% 11. 82% 9. 10% 7. 00% 11. 36% 8. 74% 6. 72% 8. 39% 6. 45% 6. 19%

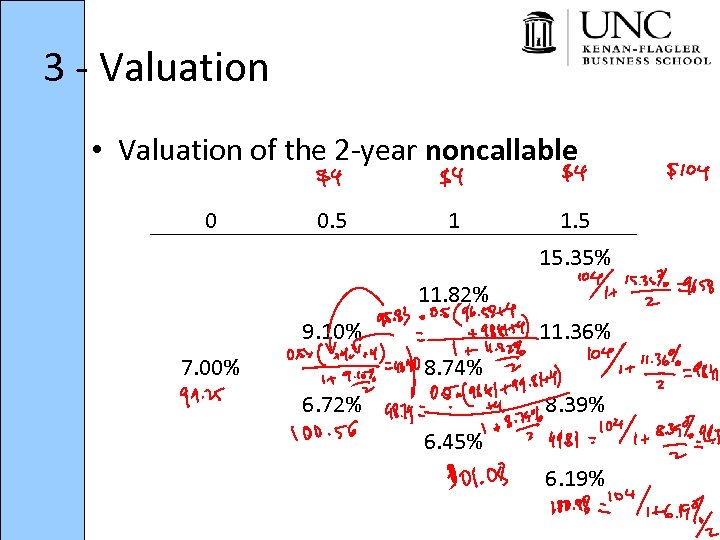
3 - Valuation • Valuation of the 2 -year noncallable 0 0. 5 1 1. 5 15. 35% 11. 82% 9. 10% 7. 00% 11. 36% 8. 74% 6. 72% 8. 39% 6. 45% 6. 19%

3 - Valuation • Valuation of the 2 -year non-callable 0 0. 5 1 1. 5 96. 5854 95. 83173 96. 90074 99. 25286 98. 40869 98. 79106 100. 5561 99. 8112 101. 082 100. 8761

3 - Valuation • Valuation of the 2 -year callable at t=1 0 0. 5 1 1. 5 96. 5854 95. 83173 96. 90074 99. 25286 98. 40869 98. 79106 100. 5561 99. 8112 101. 082 100. 8761

3 - Valuation • Valuation of the 2 -year callable at t=1. 5, 1 96. 5854 95. 83173 96. 90074 99. 25286 98. 40869 98. 79106 100. 5561 99. 8112 101. 082 100. 8761

4 – Spread due to optionality • 2 -yr non-callable: $99. 25 • 2 -yr callable: $99. 00 0 0. 5 1 1. 5 15. 35% 11. 82% 9. 10% 7. 00% 11. 36% 8. 74% 6. 72% 8. 39% 6. 45% 6. 19%

4 – Spread due to optionality • Without the tree, we can price the bond as follows: – 2 -yr non-callable: – 2 -yr callable:

4 – Spread due to optionality • Spread due to optionality: the extra premium added to the risk-free discount rates to account for the optionality of the bond

5 – Z-spread • When the investor learns: the 2 -yr callable is defaultable and illiquid, he decides to pay less for it: $98. – 2 -yr callable

5 – Z-spread • Z - spread: the extra premium added to the risk-free discount rates to account for – the optionality of the bond – the default risk of the bond – the liquidity risk of the bond • Z - spread: – total spread – zero-volatility spread – static spread

6 – Option-adjusted spread • Question: given default and liquidity risk, if the 2 -yr callable is worth $98, how much is the 2 -yr non-callable worth? • Z-spread = spread due to optionality + spread due to default/illiquidity • How can we get rid of optionality part?

6 – Option-adjusted spread • To account for default and liquidity risk, we will push the risk free interest rate tree up by a constant 15. 35% + s 11. 82% + s 9. 1% + s 7% + s 11. 36% + s 8. 74% + s 6. 72% + s 8. 39% + s 6. 45% + s 6. 19% + s

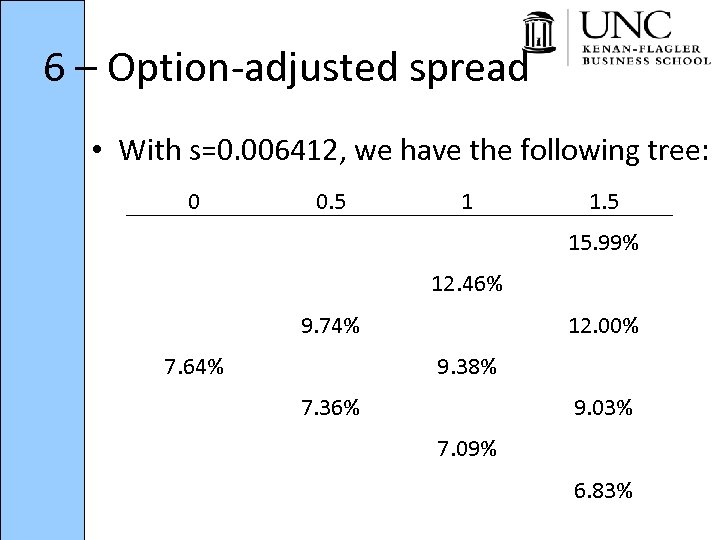
6 – Option-adjusted spread • With s=0. 006412, we have the following tree: 0 0. 5 1 1. 5 15. 99% 12. 46% 9. 74% 7. 64% 12. 00% 9. 38% 7. 36% 9. 03% 7. 09% 6. 83%

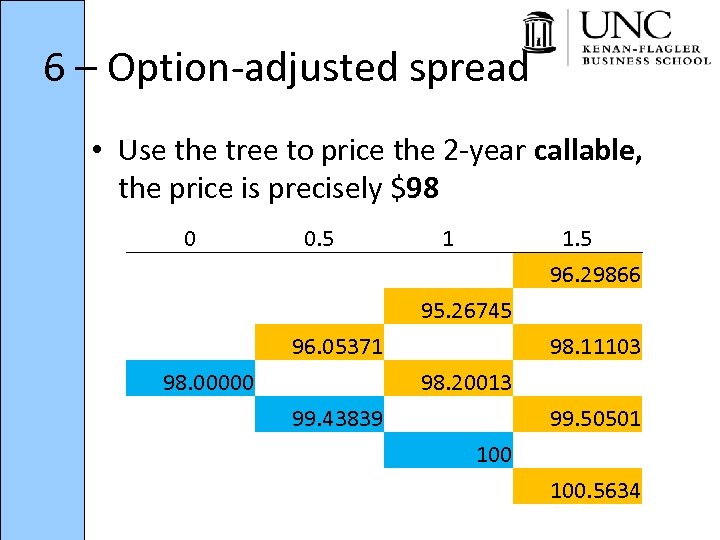
6 – Option-adjusted spread • Use the tree to price the 2 -year callable, the price is precisely $98 0 0. 5 1 1. 5 96. 29866 95. 26745 96. 05371 98. 00000 98. 11103 98. 20013 99. 43839 99. 50501 100. 5634

6 – Option-adjusted spread • 2 -yr Non-callable: $99. 25 • + callability: $99. 00 • + defaultability & illiquidity: $98. 00 • 2 price reductions: – Reduction due to callability – Reduction due to defaultability and illiquidity • These two reductions occur differently in our tree!

6 – Option-adjusted spread • The callable feature is accounted for by physically lowering the values of the bonds when optimally called • As such the spread s=0. 006412 only pertains to: – Default risk – Liquidity risk

6 – Option-adjusted spread • Option-adjusted spread: the extra premium added to the risk-free discount rates to account for – the default risk of the bond – the liquidity risk of the bond • Option-adjusted spread: the Z-spread with the optionality component taken out • Z-spread = OAS + spread due to optionality

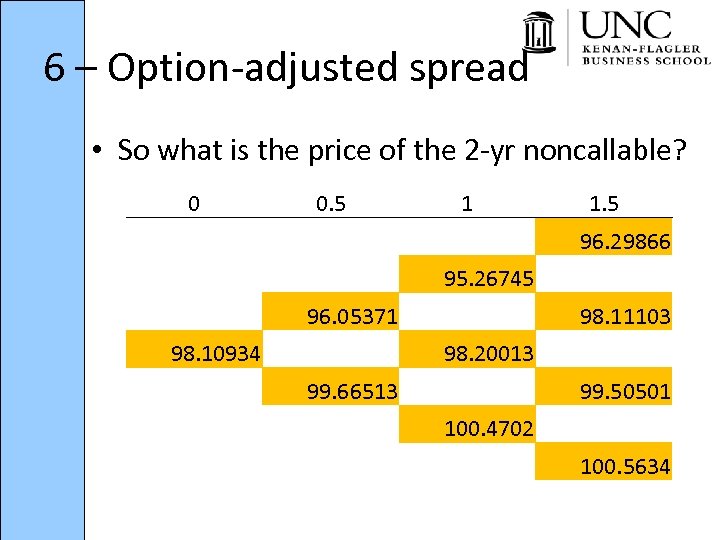
6 – Option-adjusted spread • So what is the price of the 2 -yr noncallable? 0 0. 5 1 1. 5 96. 29866 95. 26745 96. 05371 98. 10934 98. 11103 98. 20013 99. 66513 99. 50501 100. 4702 100. 5634

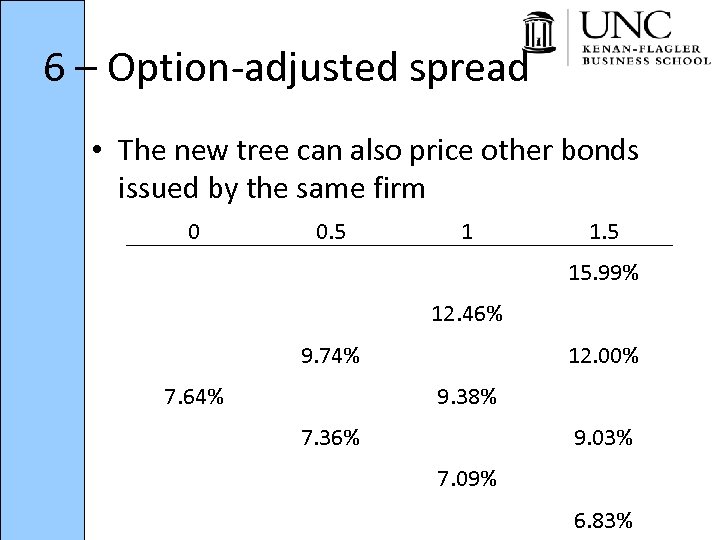
6 – Option-adjusted spread • The new tree can also price other bonds issued by the same firm 0 0. 5 1 1. 5 15. 99% 12. 46% 9. 74% 7. 64% 12. 00% 9. 38% 7. 36% 9. 03% 7. 09% 6. 83%

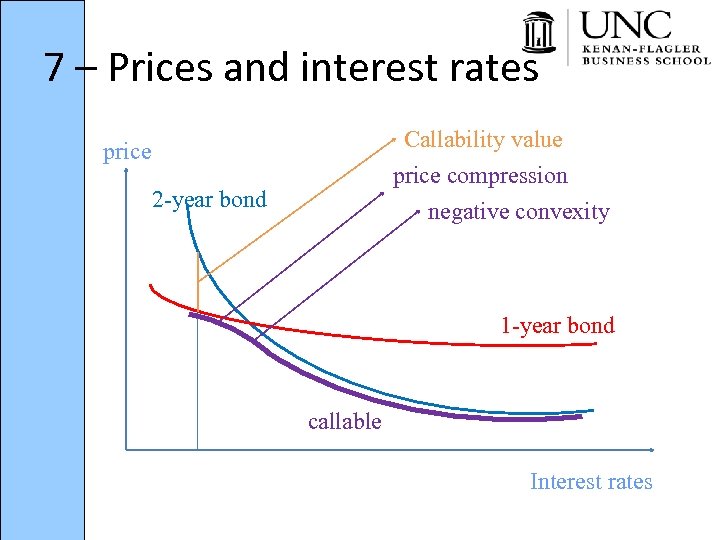
7 – Prices and interest rates Callability value price compression negative convexity 2 -year bond 1 -year bond callable Interest rates

7 – Prices and interest rates

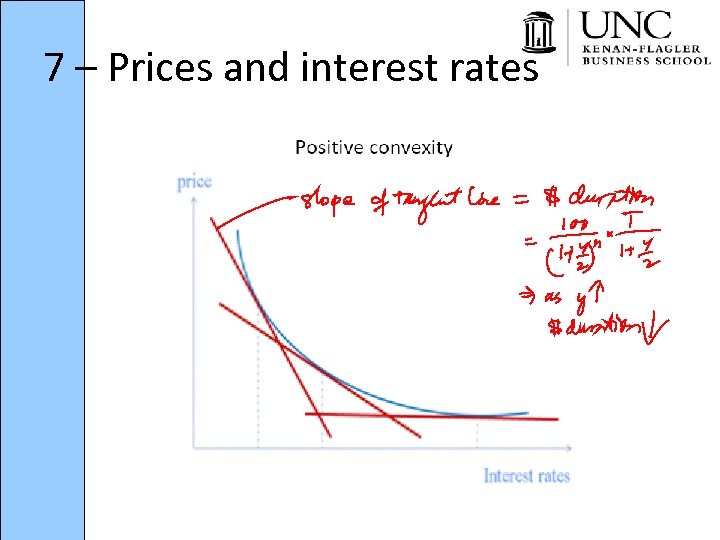
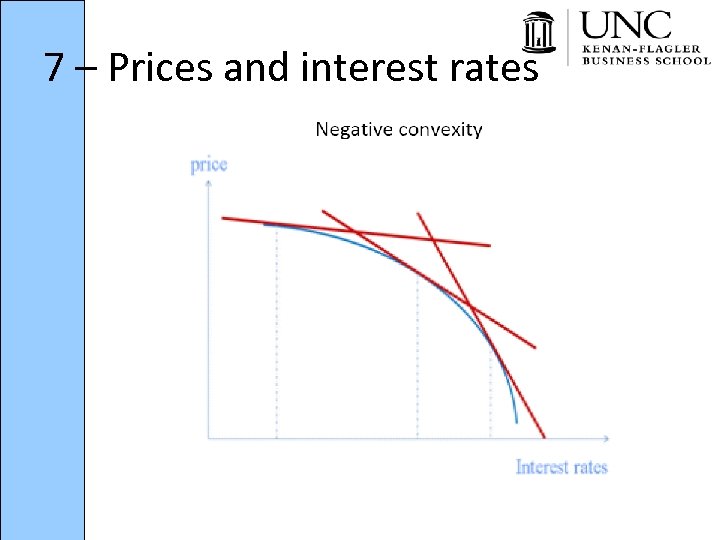
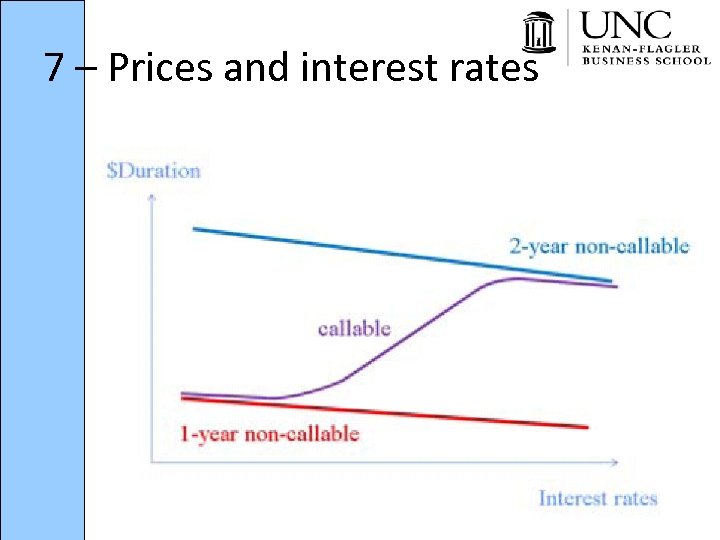
7 – Prices and interest rates • Precisely because of the increase in duration when yields increase in the middle range, callable bonds can have negative convexity • Implications for banks who buy mortgages that have negative convexity

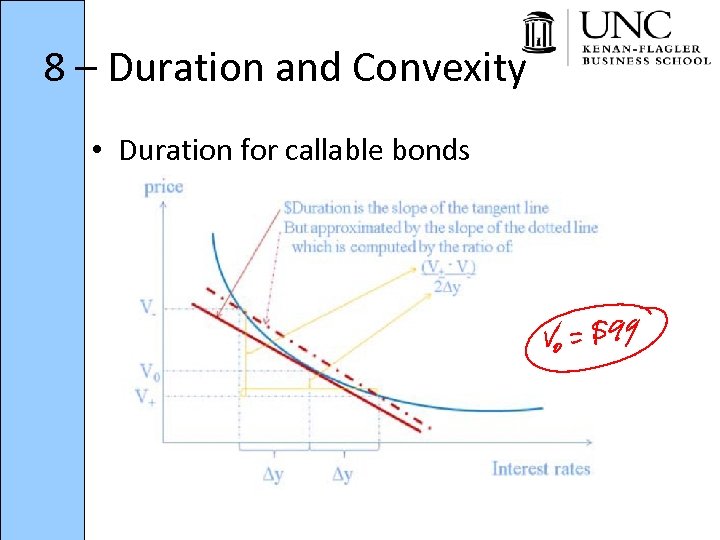
8 – Duration and Convexity • Duration for callable bonds

8 – Duration and Convexity • How to calculate V+ 15. 35% + 0. 0010 11. 82% + 0. 0010 9. 1% + 0. 0010 7% + 0. 0010 11. 36% + 0. 0010 8. 74% + 0. 0010 6. 72% + 0. 0010 8. 39% + 0. 0010 6. 45% + 0. 0010 6. 19% + 0. 0010

8 – Duration and Convexity • How to calculate V- 15. 35% - 0. 0010 11. 82% - 0. 0010 9. 1% - 0. 0010 7% - 0. 0010 11. 36% - 0. 0010 8. 74% - 0. 0010 6. 72% - 0. 0010 8. 39% - 0. 0010 6. 45% - 0. 0010 6. 19% - 0. 0010

8 – Duration and Convexity • Dollar Duration = • Dollar Convexity = • Convexity =