 Calculus Ch. 3. Continuity of a function
Calculus Ch. 3. Continuity of a function
 Question 1 (October 2011 Exam, Q 3). A function f (x) is continuous for all positive values of x and for all negative values of x. Which of the following sets can not be the range of f (x)? a) R; Solution: In order to show that a set A can be the range of f (x) it is sufficient to present an example of a function f (x) with E( f ) = A.
Question 1 (October 2011 Exam, Q 3). A function f (x) is continuous for all positive values of x and for all negative values of x. Which of the following sets can not be the range of f (x)? a) R; Solution: In order to show that a set A can be the range of f (x) it is sufficient to present an example of a function f (x) with E( f ) = A.
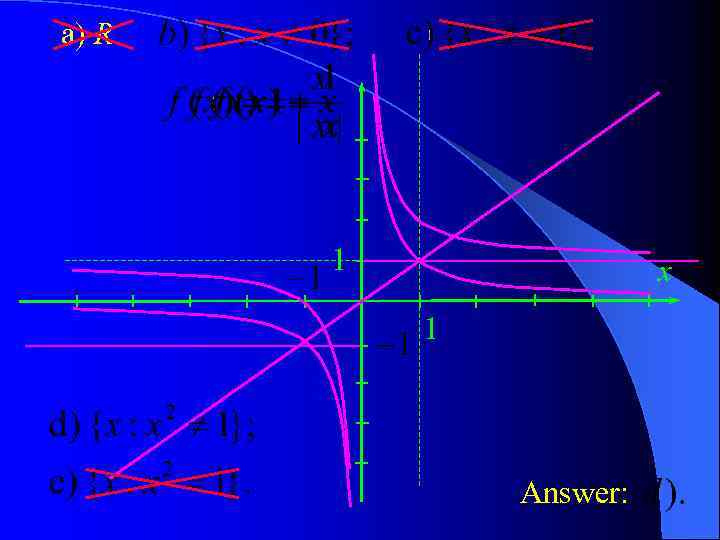 a) R 1 x 1 Answer:
a) R 1 x 1 Answer:
 Calculus Ch. 4. The Derivative Frequently used notations: The main rules:
Calculus Ch. 4. The Derivative Frequently used notations: The main rules:
 The chain rule: For example: Here Hence For example: and
The chain rule: For example: Here Hence For example: and
 Question 2 (October 2011 Exam, Q 7). Calculate the derivative of the function Answer: a).
Question 2 (October 2011 Exam, Q 7). Calculate the derivative of the function Answer: a).
 Question 3 (November 2007 Exam, Q 24). Which of the following statements is or are true? a) I and II only, b) I and III only, c) III only, d ) II and III only, e) I, II, and III. Answer: c).
Question 3 (November 2007 Exam, Q 24). Which of the following statements is or are true? a) I and II only, b) I and III only, c) III only, d ) II and III only, e) I, II, and III. Answer: c).
 Question 4. Consider the function Calculate the derivative Find its points of discontinuity and determine their type. Solution. We have
Question 4. Consider the function Calculate the derivative Find its points of discontinuity and determine their type. Solution. We have
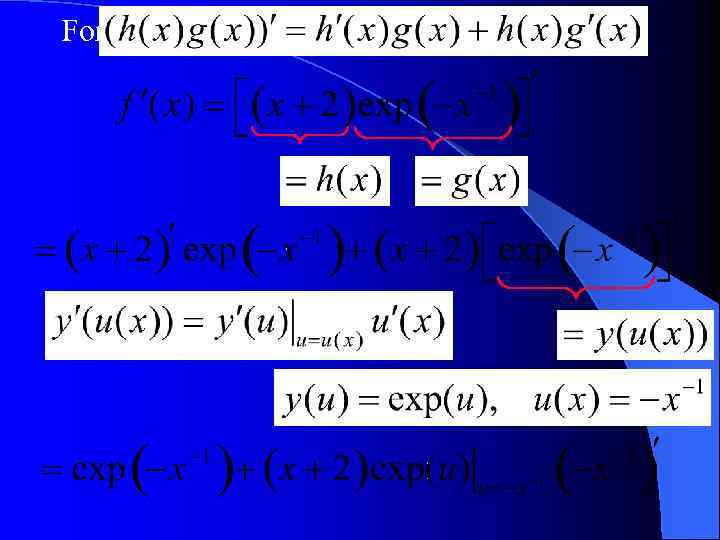 For
For
 Hence, for For The derivative has special points at and at
Hence, for For The derivative has special points at and at
 Hence the derivative has Type I discontinuity at
Hence the derivative has Type I discontinuity at
 The exponential function tends to 0 faster than any power function tends to Hence the derivative has Type II discontinuity at Answer: Type I discontinuity at x = -2, and Type II discontinuity at x = 0.
The exponential function tends to 0 faster than any power function tends to Hence the derivative has Type II discontinuity at Answer: Type I discontinuity at x = -2, and Type II discontinuity at x = 0.
 Question 5 (January 2008 Exam, Q 13). For what value of m will the function be differentiable for all x? a) -1, b) 0, c) ½, d) 1, e) There is no such m. Solution. The left derivative of the function f (x) at x = 0 is given by
Question 5 (January 2008 Exam, Q 13). For what value of m will the function be differentiable for all x? a) -1, b) 0, c) ½, d) 1, e) There is no such m. Solution. The left derivative of the function f (x) at x = 0 is given by
 The right derivative at x = 0 is given by The function f (x) is differentiable at x = 0 if it is continuous there and the left derivative is equal to the right derivative. That is, if Check continuity: Answer:
The right derivative at x = 0 is given by The function f (x) is differentiable at x = 0 if it is continuous there and the left derivative is equal to the right derivative. That is, if Check continuity: Answer: