CAD Graphics Hong Kong Dec 7 -10 2005 Interactive

CAD/Graphics, Hong Kong, Dec. 7 -10, 2005 Interactive, Procedural Computer-Aided Design Carlo H. Séquin EECS Computer Science Division University of California, Berkeley

CAD Tools for the Early and Creative Phases of Design u Tutorial u E-CAD Examples Lessons for M-CAD, CAGD

Outline I. The Power of u Parametric Procedural Design u Computer-Aided u CAD Optimization / Synthesis Tools for the Early Phases of Design u Evolution u Towards (G. A. ) versus Intelligent Design an Integrated CAD Environment

Julia Sets, Mandelbrot Set, Fractals Defined by just a few numbers. . .

Sculptures by Brent Collins (1980 -94)

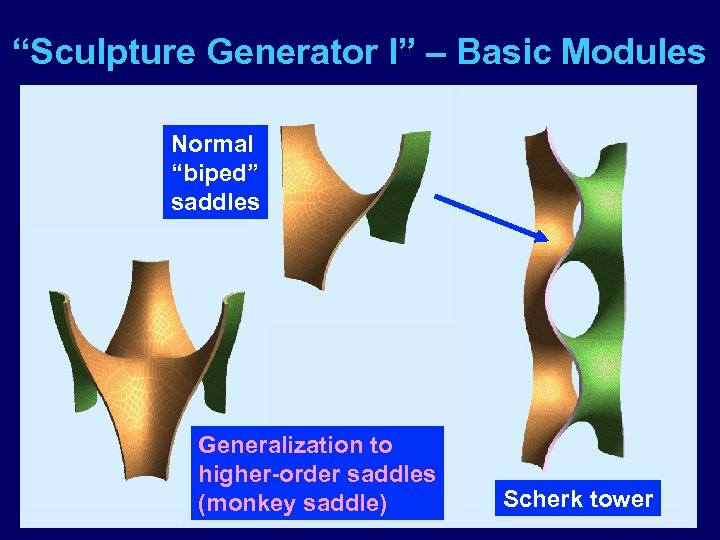“Sculpture Generator I” – Basic Modules Normal “biped” saddles Generalization to higher-order saddles (monkey saddle) Scherk tower

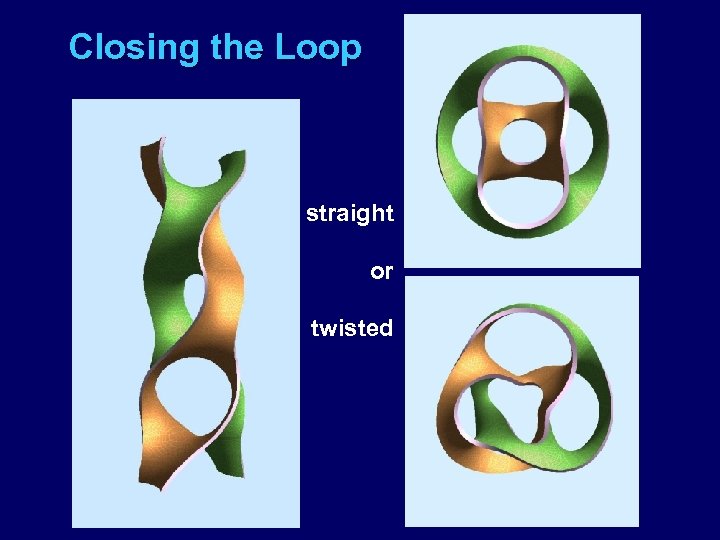Closing the Loop straight or twisted

“Sculpture Generator I”, GUI These parameters define sculpture; = “genome”

Brent Collins & Hyperbolic Hexagon II

12 -foot Snow Sculpture Silver medal, Breckenridge, Colorado, 2004

. . . and a Whole Lot of Plastic Models

Bronze Sculpture Done by investment casting from FDM original

“Natural” Forms by Albert Kiefer, sent by Johan Gielis, developer of supergraphx u made with supergraphx www. genicap. com

The “genome” is the ultimate parameterization of a design, given the proper procedure to interpret that code u Without the proper framework, the genome is meaningless. (e. g. , human DNA on a planet in the Alpha-Centauri System)

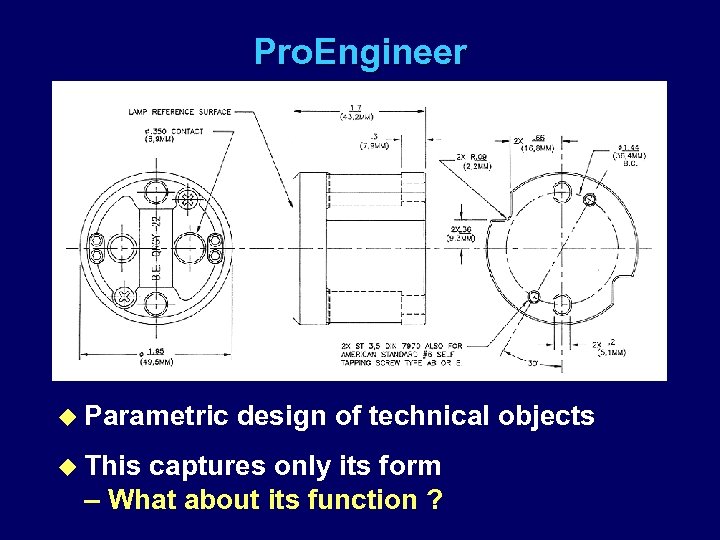Pro. Engineer u Parametric u This design of technical objects captures only its form – What about its function ?

What Shape Has the Right Functionality?

How Do We Know What Makes a Good Design With Proper Functionality ? e. g. a comfortable razor ? or a better mouse-trap ? u. Traditional Approach: Trial and Error (T&E)

T&E: OK for Early Flying Machines

T&E: Not OK for Nuclear Power Plants OK ! – this one seems to work !!

CAD for Design Verification u Do expensive or dangerous experiments on the computer. u Use: u E. g. , calculations, analysis, simulation. . . SPICE (Simulation Program with Integrated Circuit Emphasis), L. W. Nagel and D. O. Pederson (1972)

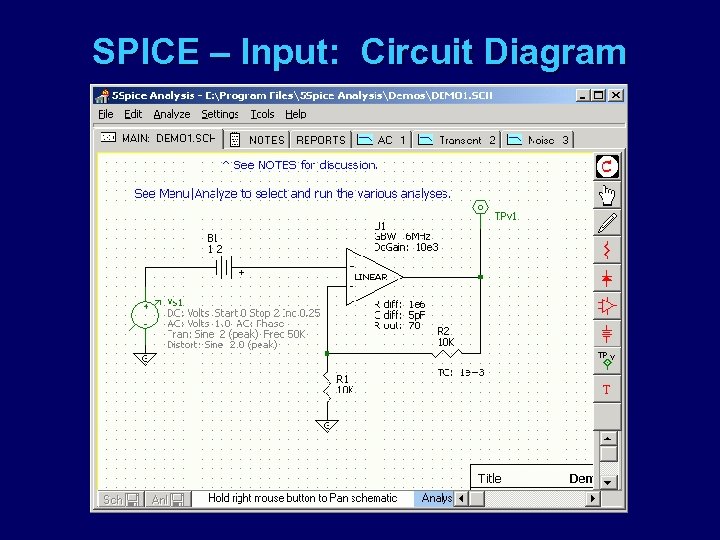SPICE – Input: Circuit Diagram

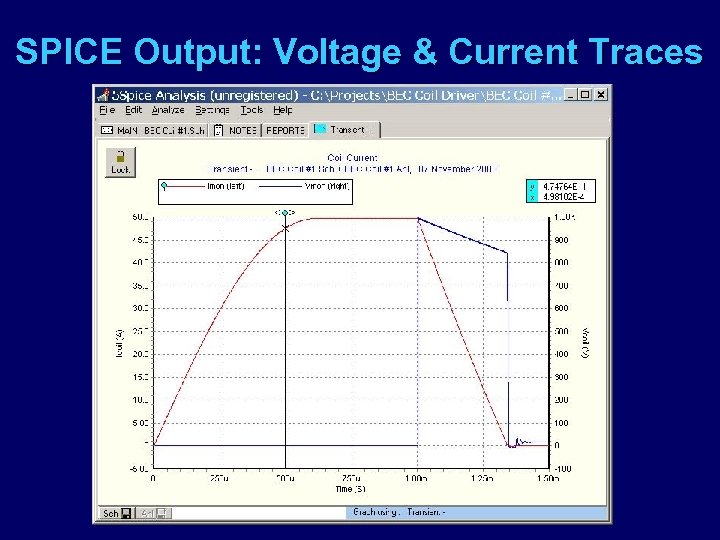SPICE Output: Voltage & Current Traces

Heuristics + Analysis Programs Computer-Aided Synthesis u Generate new designs based on well-established heuristics. u Use evaluation CAD tools in an inner loop. u Now: u First Parameterize the desired function. proven in domain of modular circuits (logic circuits, filters, op-amps. . . )

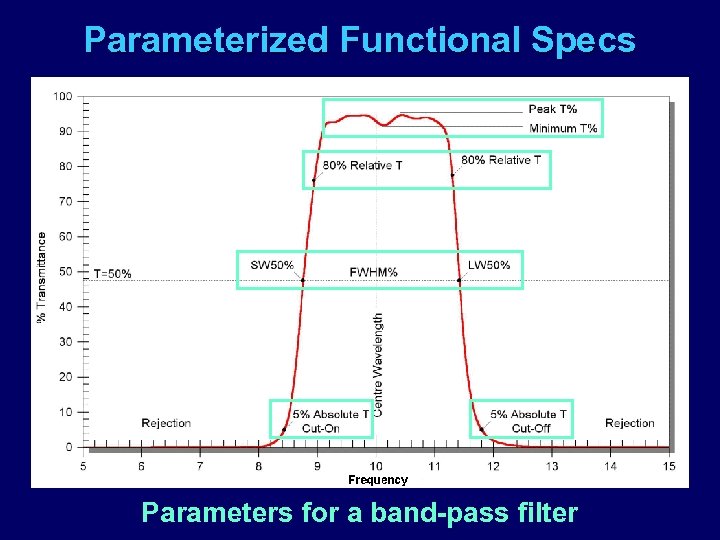Parameterized Functional Specs Parameters for a band-pass filter

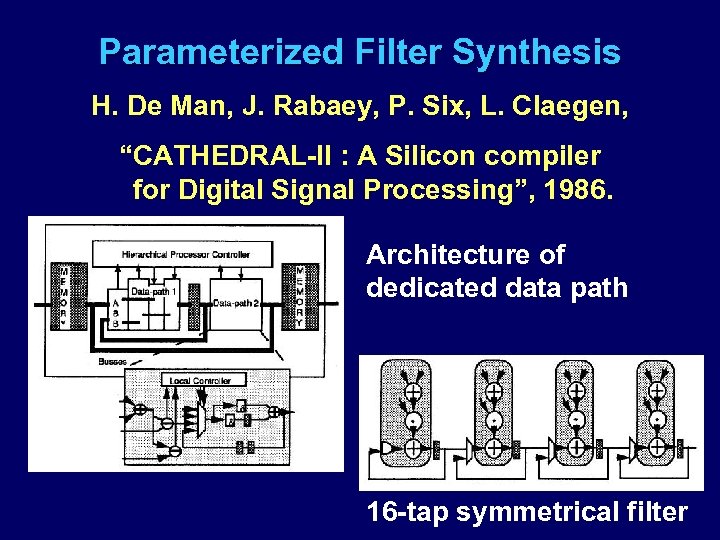Parameterized Filter Synthesis H. De Man, J. Rabaey, P. Six, L. Claegen, “CATHEDRAL-II : A Silicon compiler for Digital Signal Processing”, 1986. Architecture of dedicated data path 16 -tap symmetrical filter

Add: Computer-Aided Optimization u Use evaluation CAD tools + a local optimization step as an inner loop in a search procedure.

OPASYN A Compiler for CMOS Operational Amplifiers H. Y. Koh, C. H. Séquin, P. R. Gray, 1990 Synthesizing on-chip operational amplifiers to given specifications and IC layout areas. 1. Case-based reasoning (heuristic pruning) selects from 5 proven circuit topologies. 2. Parametric circuit optimization to meet specs. 3. IC layout generation based on macro cells.

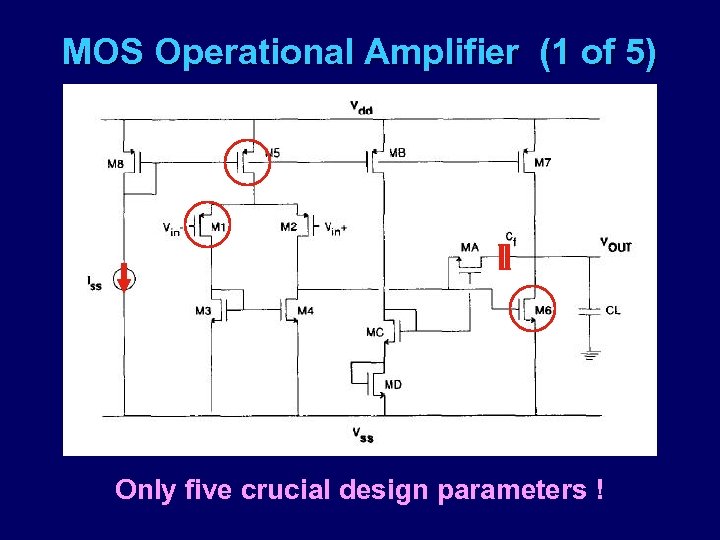MOS Operational Amplifier (1 of 5) Only five crucial design parameters !

Op-Amp Design (OPASYN, 1990) Multiple Objectives: u output voltage swing (V) u output slew rate (V/nsec) u open loop gain () u settling time (nsec) u unity gain bandwidth (MHz) u 1/f-noise (V*Hz-½) u power dissipation (m. W) u total layout area (mm 2) “Cost” of Design = weighted sum of deviations Optimization: minimize cost

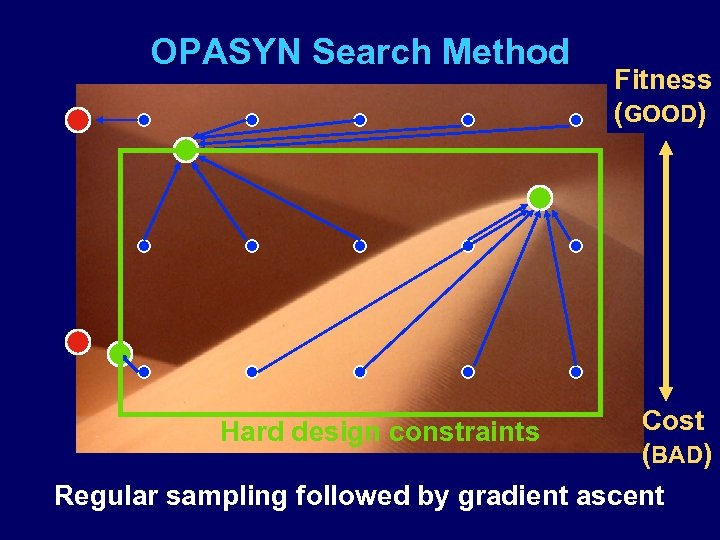OPASYN Search Method Fitness (GOOD) Cost (BAD) 5 D design-parameter space Regular sampling followed by gradient ascent Hard design constraints

MOS Op-Amp Layout u Following circuit synthesis & optimization, other heuristic optimization procedures produce layout with desired aspect ratio.

Synthesis in Established Fields u Filter design and MOS Op-Amp synthesis have well-established engineering practices. u Efficiently parameterized designs as well as robust and efficient design procedures exist. u Experience is captured in special-purpose programs and used for automated synthesis. u But what if we need to design something new in “uncharted engineering territory” ?

Uncharted Territory u Task: u How Design a robot that climbs trees ! do you get started ? ?

An Important New Phase is Prepended to the Design Process: Idea Generation, Exploration. . .

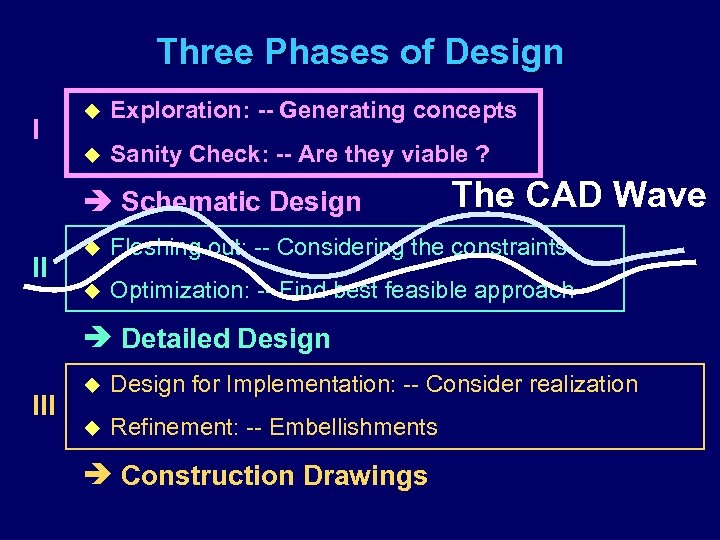Three Phases of Design Exploration: -- Generating concepts u I u Sanity Check: -- Are they viable ? Schematic Design II The CAD Wave u Fleshing out: -- Considering the constraints u Optimization: -- Find best feasible approach Detailed Design III u Design for Implementation: -- Consider realization u Refinement: -- Embellishments Construction Drawings

Quality / Maturity of CAD Tools I Gathering ideas, generating concepts u POOR Schematic Design II Considering constraints, finding best approach u MARGINAL Detailed Design III Refinement, embellishments, realization u GOOD Construction Drawings

Activities in Phase I How do people come up with new ideas ? u Doodles, sketches, brain-storming, make wish-lists, bend wires, carve styrofoam, . . . What CAD tools do we need to help ? u Create novel conceptual prototypes. . . u Evaluate u Show them, rank order them. . . promising ones to user … How do we automate that search ?

“Holey” Fitness Space u Open-ended engineering problems have complicated, higher-dimensional solution / fitness spaces.

Genetic Algorithms u Pursue several design variations in parallel (many “phenotypes” in each generation) u Evaluate their “fitness” (how well they meet the various design objectives “Pareto set”) u Use best designs to “breed” new off-springs (by modifying some genes = “mutation”) (by exchanging genes = “crossover”) u Expectation: Good traits will survive, bad features will be weeded out. . .

How Well Do G. A. Work for Engineering Tasks ? An Experiment: Let ME students design a MEMS resonator u Students u Good (initially) had no IC experience programmers u Excited about Genetic Algorithms

Micro-Electromechanical Systems MEMS u Created with an enhanced fabrication technology used for integrated circuits. u Many nifty devices and systems have been built: motors, steerable mirrors, accelerometers, chemo sensors. . .

MEMS Example u Ciliary Micromanipulator, K. Böhringer et al. Dartmouth, 1997.

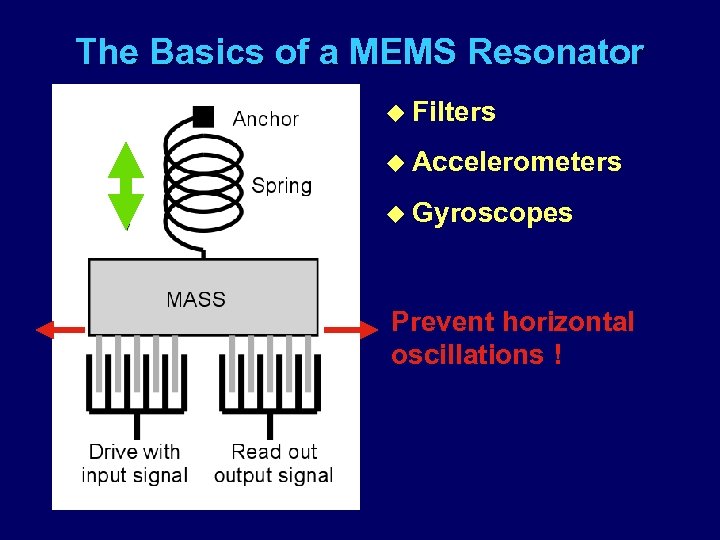The Basics of a MEMS Resonator u Filters u Accelerometers u Gyroscopes Prevent horizontal oscillations !

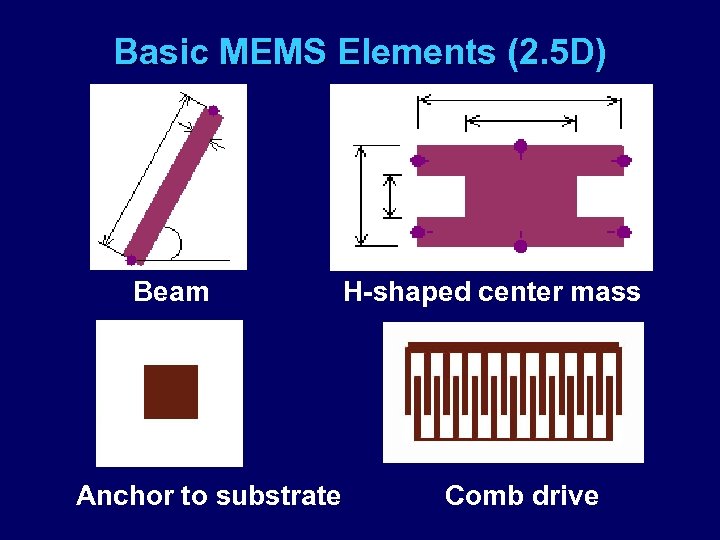Basic MEMS Elements (2. 5 D) Beam Anchor to substrate H-shaped center mass Comb drive

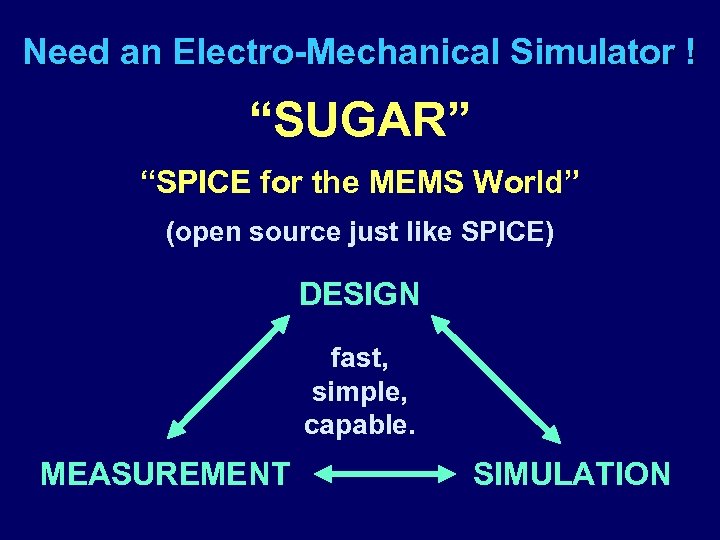Need an Electro-Mechanical Simulator ! “SUGAR” “SPICE for the MEMS World” (open source just like SPICE) DESIGN fast, simple, capable. MEASUREMENT SIMULATION

The SUGAR Abstraction Digital-to-Analog Converter by R. Yej, K. S. J. Pister

SUGAR in Action. . . Multimode Resonator by R. Brennen

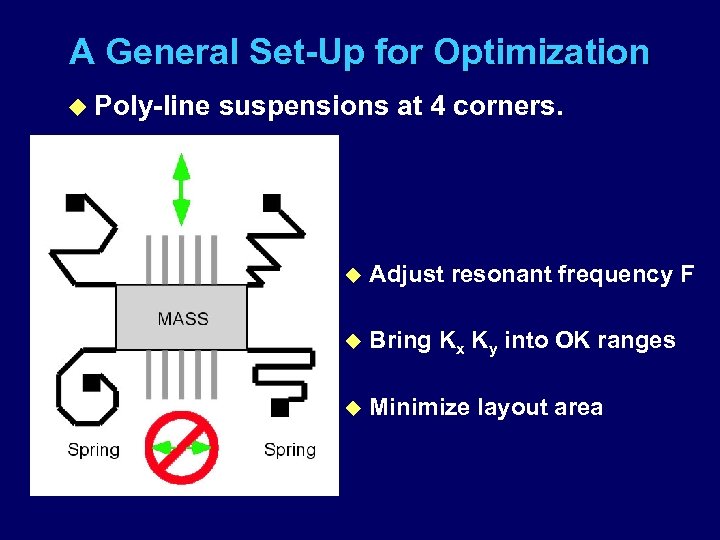A General Set-Up for Optimization u Poly-line suspensions at 4 corners. u Adjust resonant frequency F u Bring Kx Ky into OK ranges u Minimize layout area

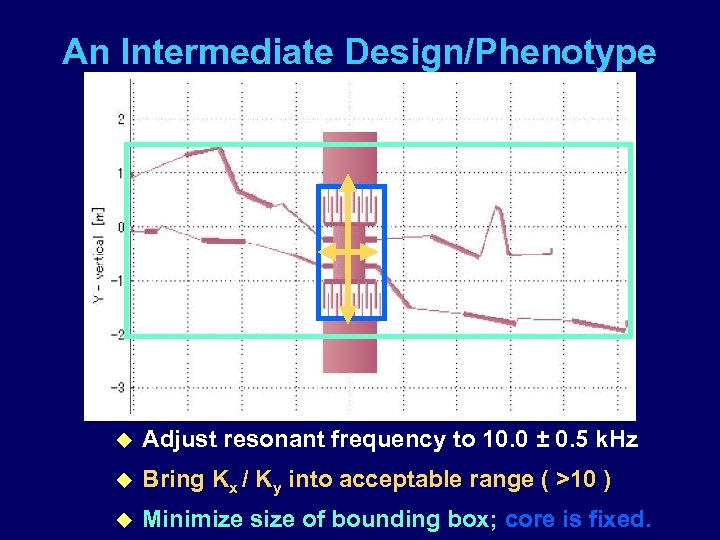An Intermediate Design/Phenotype u Adjust resonant frequency to 10. 0 ± 0. 5 k. Hz u Bring Kx / Ky into acceptable range ( >10 ) u Minimize size of bounding box; core is fixed.

MEMS Actually Built and Measured

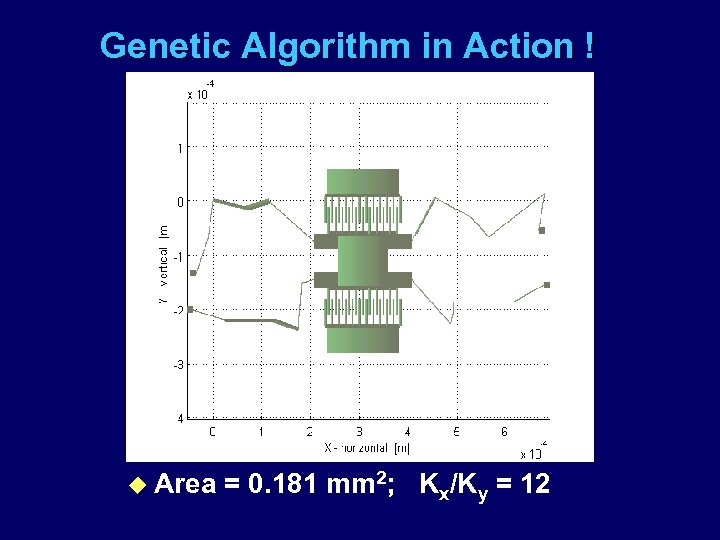Genetic Algorithm in Action ! u Area = 0. 181 mm 2; Kx/Ky = 12

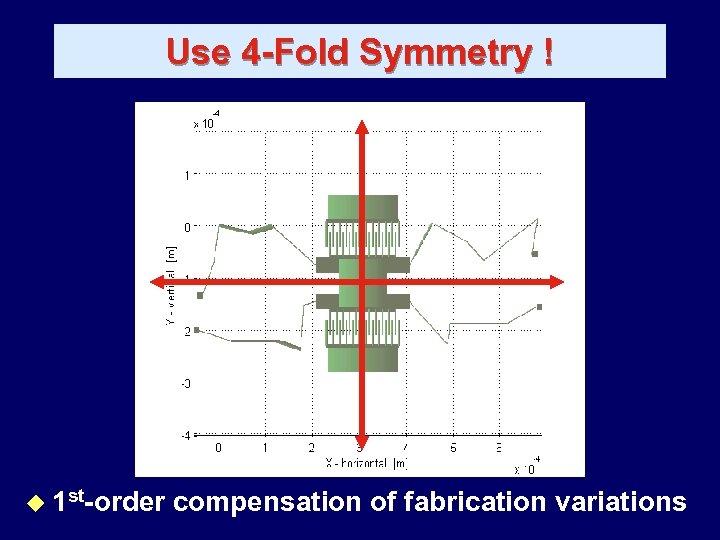Use 4 -Fold Symmetry ! u 1 st-order compensation of fabrication variations

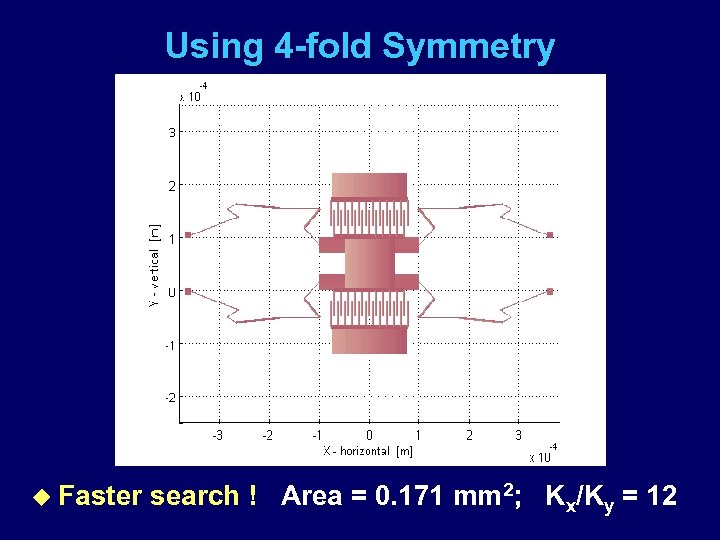Using 4 -fold Symmetry u Faster search ! Area = 0. 171 mm 2; Kx/Ky = 12

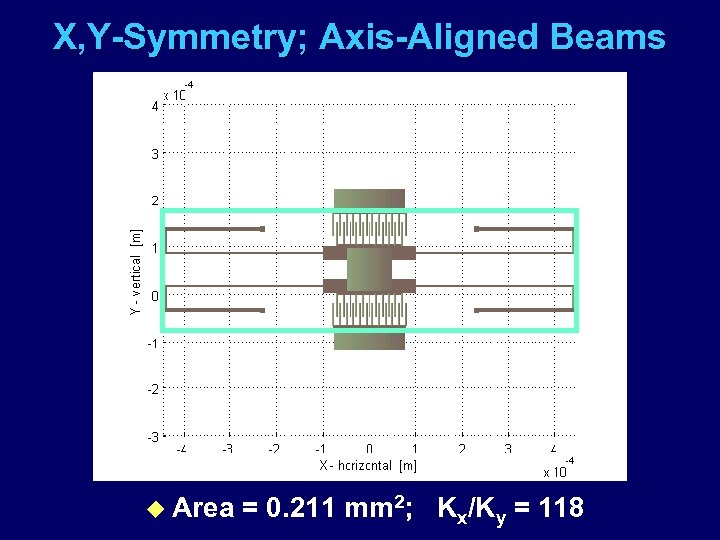X, Y-Symmetry; Axis-Aligned Beams u Area = 0. 211 mm 2; Kx/Ky = 118

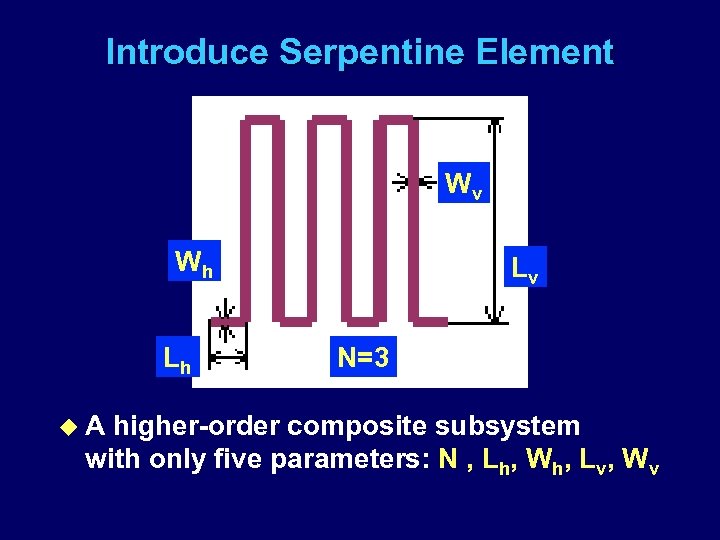Introduce Serpentine Element Wv Wh Lh u. A Lv N=3 higher-order composite subsystem with only five parameters: N , Lh, Wh, Lv, Wv

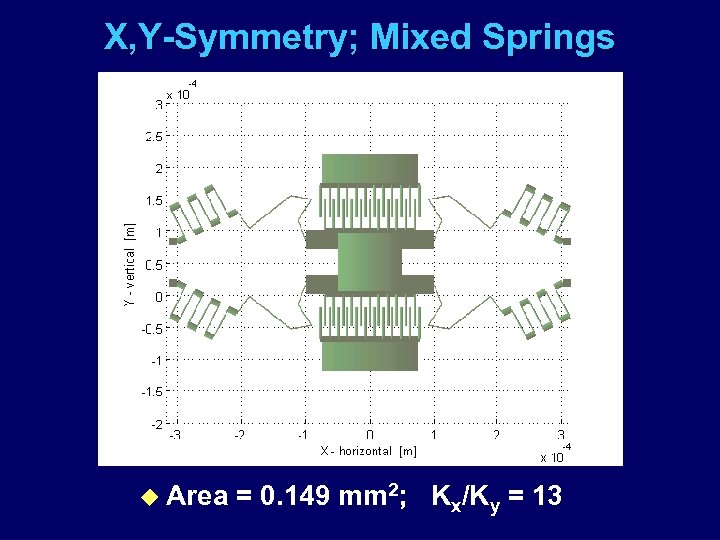X, Y-Symmetry; Mixed Springs u Area = 0. 149 mm 2; Kx/Ky = 13

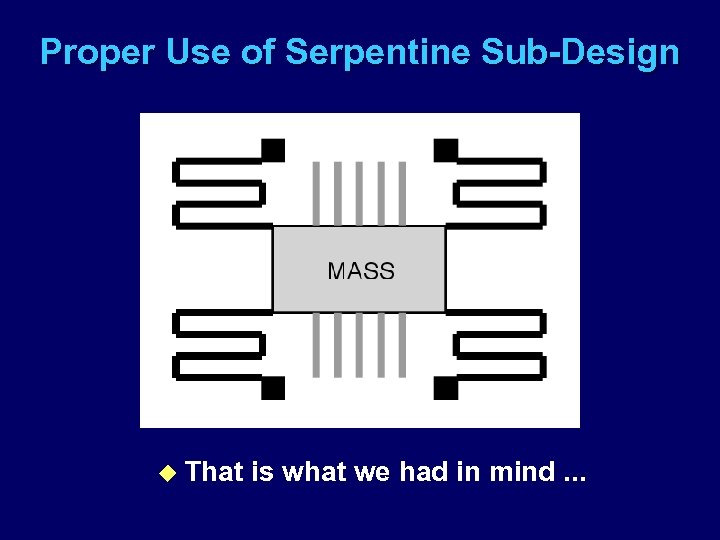Proper Use of Serpentine Sub-Design u That is what we had in mind. . .

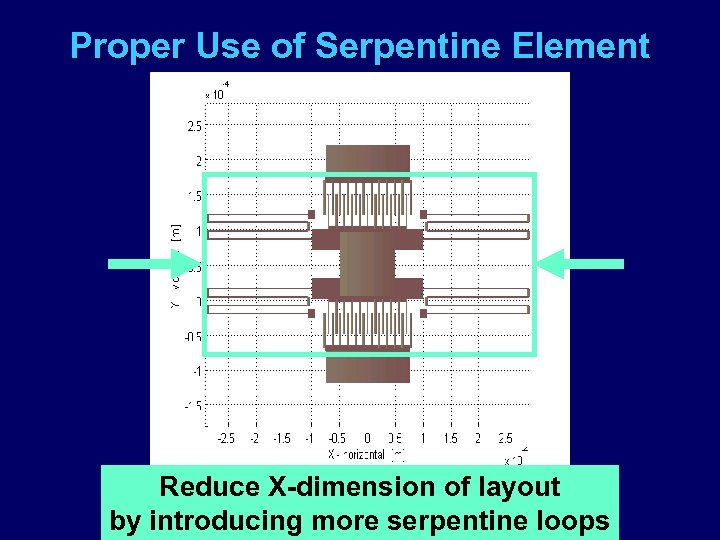Proper Use of Serpentine Element Reduce 0. 143 mm 2; u Area =X-dimension ofxlayout K /Ky = 11 by introducing more serpentine loops

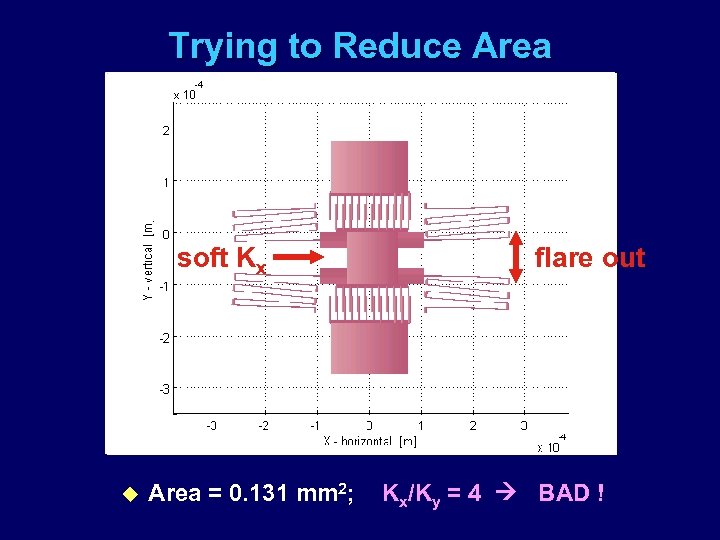Trying to Reduce Area soft Kx u Area = 0. 131 mm 2; flare out Kx/Ky = 4 BAD !

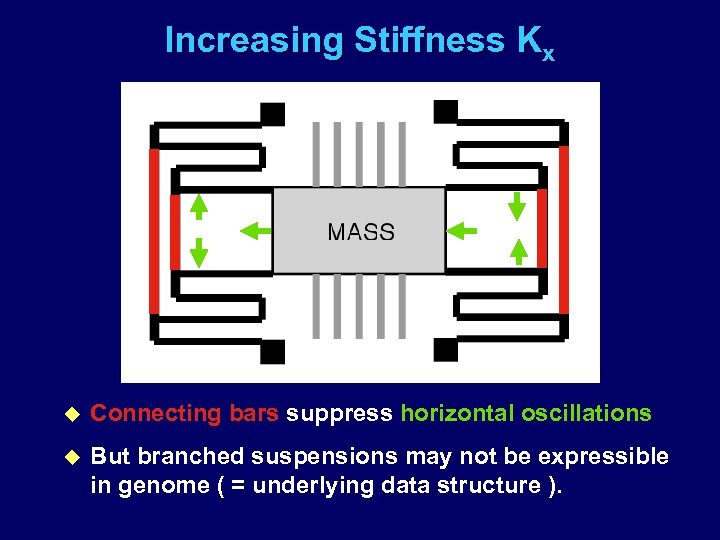Increasing Stiffness Kx u Connecting bars suppress horizontal oscillations u But branched suspensions may not be expressible in genome ( = underlying data structure ).

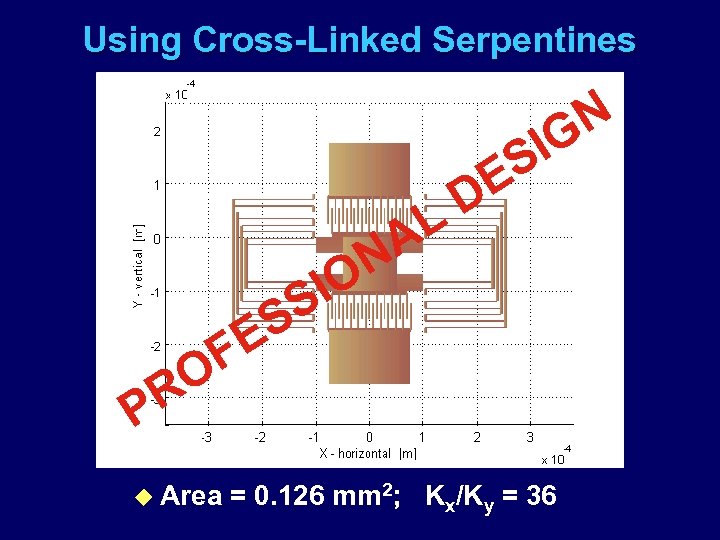Using Cross-Linked Serpentines N IG S E D L A N S E F O IO S R P u Area = 0. 126 mm 2; Kx/Ky = 36

What really happened here ? u Major improvement steps came by engineering insights. u Genetic algorithm found good solutions for the newly introduced configurations. u With only few parameters & clear objectives, greedy optimization may be more efficient. u With complex multiple objectives, G. A. may have advantage of parallel exploration.

Why Did the G. A. Not Find This ? u Lack of expressibility of genome. u Solution space too large, too rugged. . . u Sampling u Samples is too sparse ! are not driven to local optima.

A Rugged Solution Space u No design lies on the very top of a peak ! u Good intermediate solutions may get lost. 20. 1. Generation drifting to high mountains Generation – – a random sampling 50. Generation – clustered nearhigher ground

What Are Genetic Algorithms Good For? u Exploring unknown territory u Generating u Showing a first set of ideas different subsystem solutions How can this be harnessed most effectively in an engineering design environment ?

Current Work Building a flexible, extensible CAD framework for exploration, ideation, design, and optimization. Test: MEMS Resonators, Filters, Gyroscopes With: u Prof. A. Agogino (ME) u Dr. Raffi Kamalian u Ying Zhang, Ph. D student u Corie Cobb , Ph. D student

Making G. A. Useful for Engineering u G. A. by itself is not a good engineering tool ! Selection of good starting phenotypes Visualization G. A. Selective breeding Suggestive editing Greedy Optimization

G. A. for Engineering Needs (1): A way to pick promising initial designs, e. g. from: ua case library u classical u internet literature searches u personal advice from experts u sketches, doodles

Our Component / Case Library Multiple levels of building blocks: l Low-level primitive design element: anchors, masses, beams, combs. . . l High-level design clusters: “I” masses, polylines, serpentines. . . l Successful designs (Case Library): mechanical resonators. . .

G. A. for Engineering Needs (2): An extensible underlying data structure, compatible with the available simulator (SUGAR) ! Fixed Structured descriptions: l Sculpture Generator I: fixed set of parameters l OPASYN: a tree of 5 basic designs (5 -8 params. ) too rigid Grammar-based representations: l Lindenmayer Systems (1968): parallel string-rewrite l “Artificial Life” by Karl Sims (1991).

Hierarchical MEMS u “Frequency-Selective MEMS for Miniaturized Communication Devices” u Clark T. -C. Nguyen, Proc. 1998 IEEE Aerospace Conf.

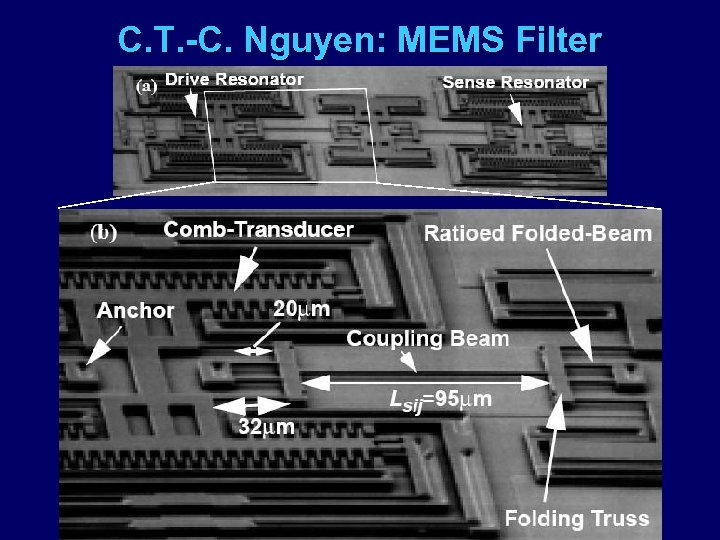C. T. -C. Nguyen: MEMS Filter

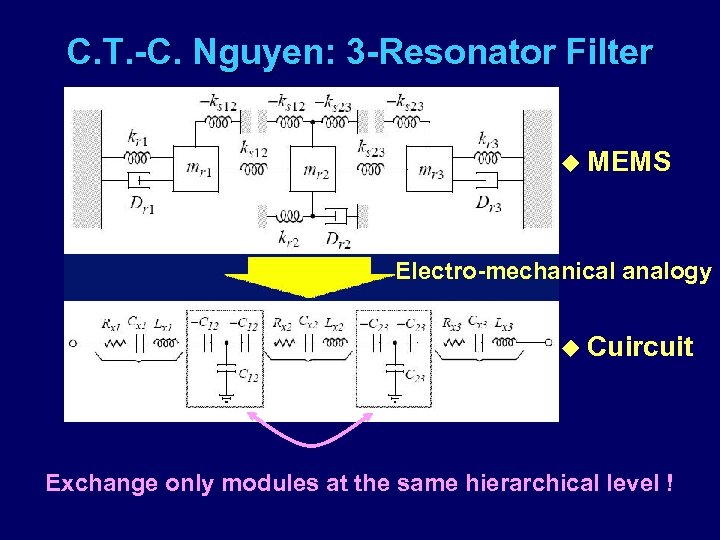C. T. -C. Nguyen: 3 -Resonator Filter u MEMS Electro-mechanical analogy u Cuircuit Exchange only modules at the same hierarchical level !

Our Representation of Designs u Object-oriented (C++) hierarchical graph: l modules with connection points; l connectivity via net list. u Parameter l set of building blocks act as genes: real, integer, and binary numbers. u Other fields indicate allowable modifications: l what can mutate, by how much; l which elements can perform genetic crossover respecting hierarchical levels !

G. A. for Engineering Needs (3): Efficient ways to predict the functionality and fitness of phenotypes: u simulator u heuristic for the appropriate domain (SUGAR) evaluations based on past experience u visualization for quick human judgment keeping common-sense control !

G. A. for Engineering Needs (4): Ways to improve the evolutionary process: u greedy phenotype optimization u deletion / advancement of special phenotypes u introducing new parameters / constraints u high-lighting of desirable features. . .

Modeling by Example u T. Funkhouser et. al, Princeton, Siggraph 2004

G. A. for Engineering Needs (5): Ways to edit individual designs: u sketching a whole new systems topology (this may be a far-out dream. . . ) u selective editing of phenotypes: “story-board” visualization of the sought-after design environment. . .

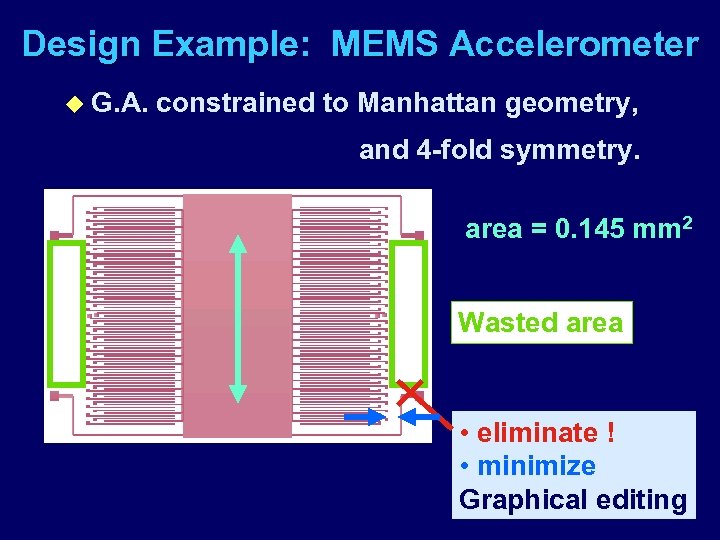Design Example: MEMS Accelerometer u G. A. constrained to Manhattan geometry, and 4 -fold symmetry. area = 0. 145 mm 2 Wasted area • eliminate ! • minimize Graphical editing

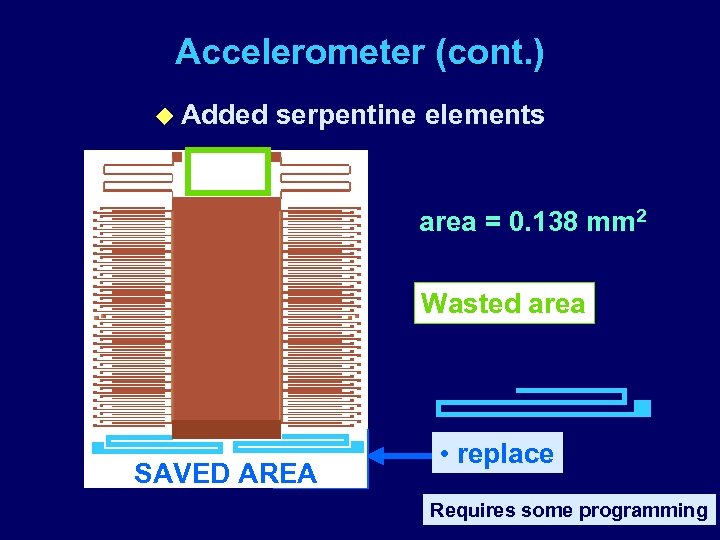Accelerometer (cont. ) u Added serpentine elements area = 0. 138 mm 2 Wasted area SAVED AREA • replace Requires some programming

Accelerometer: Result u New, more compact serpentine (fewer params) area = 0. 113 mm 2 Do we really need G. A. to find this solution ? ? We definitely need engineering intelligence !

Summary u CAD will not become fully automated anytime soon. u Human intelligence will continue to play a key role: l engineering experience l common sense u It must be more tightly integrated into the design process: faster design completion better design results

Today’s CAD Environments for Phase I u corresponding state of the art. . .

CAD Environments of the Future u Phase_1 CAD tools have a long way to go yet ! u Encourage bright young minds to work in this field.

QUESTIONS ?

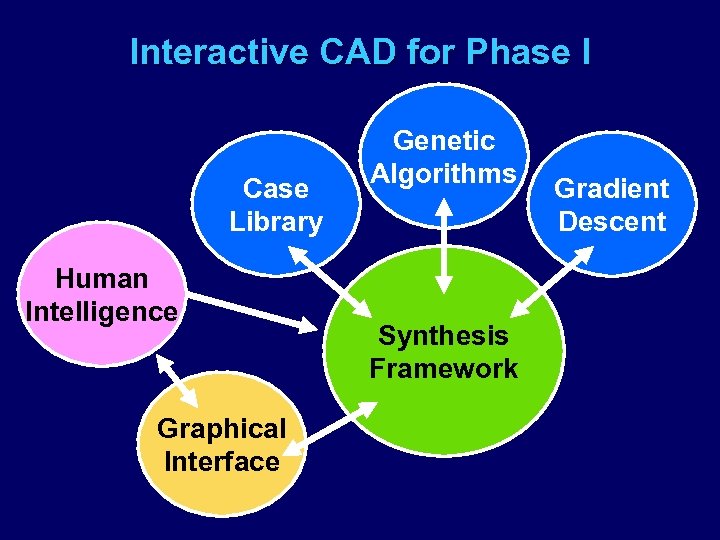Interactive CAD for Phase I Case Library Human Intelligence Graphical Interface Genetic Algorithms Synthesis Framework Gradient Descent