Caching in Backtracking Search Fahiem Bacchus University of Toronto
Introduction Backtracking search needs only space linear in the number of variable (modulo the size of the problem representation). However, its efficiency can greatly benefit from using more space to cache information computed during search. Caching can provable yield exponential improvements in the efficiency of backtracking search. Caching is an any-space feature. We can use as much or as little space for caching as we want without affecting soundness or completeness. Unfortunately, caching can also be time consuming. How do we exploit theoretical potential of caching in practice? 2 Fahiem Bacchus, University of Toronto 3/15/2018
Introduction We will examine this question for The problem of finding a single solution And for problems that require considering all solutions Counting the number of solutions/computing probabilities Finding optimal solutions. We will look at 3 The theoretical advantages offered by caching. Some of the practical issues involved with realizing these theoretical advantages. Some of the practical benefits obtained so far. Fahiem Bacchus, University of Toronto 3/15/2018
Outline Caching when searching for a single solution. 1. Clause learning in SAT. Clause learning in CSPs. Caching when considering all solutions. 2. Formula caching for sum of products problems 4 Theoretical results. Its practical application and impact. Theoretical results. Practical application Fahiem Bacchus, University of Toronto 3/15/2018
1. 5 Caching when searching for a single solution Fahiem Bacchus, University of Toronto 3/15/2018
1. 1 Clause Learning in SAT 6 Fahiem Bacchus, University of Toronto 3/15/2018
Clause Learning in SAT (DPLL) Clause learning is the most successful form of caching when searching for a single solution [Marques-Silva and Sakallah, 1996; Zhang et al. , 2001]. Has revolutionized DPLL SAT solvers (i. e. , Backtracking SAT solvers). 7 Fahiem Bacchus, University of Toronto 3/15/2018
Clause Learning in SAT 1. Branch on a variable 2. Perform Propagation Unit Propagation 8 Fahiem Bacchus, University of Toronto 3/15/2018
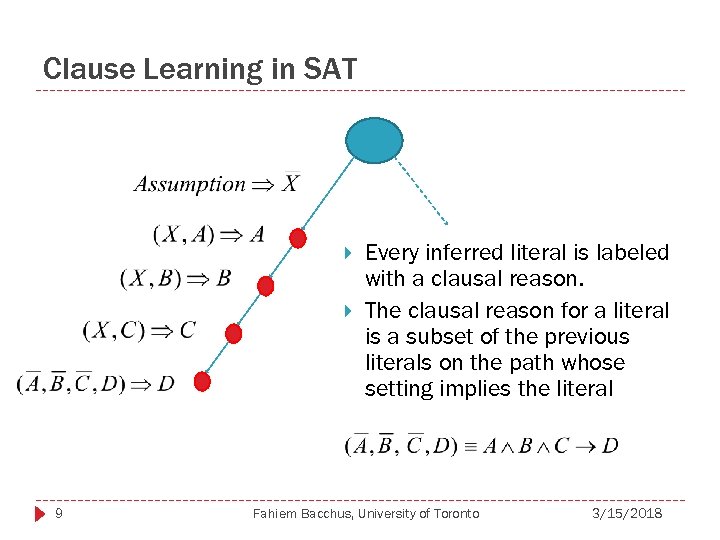
Clause Learning in SAT 9 Every inferred literal is labeled with a clausal reason. The clausal reason for a literal is a subset of the previous literals on the path whose setting implies the literal Fahiem Bacchus, University of Toronto 3/15/2018
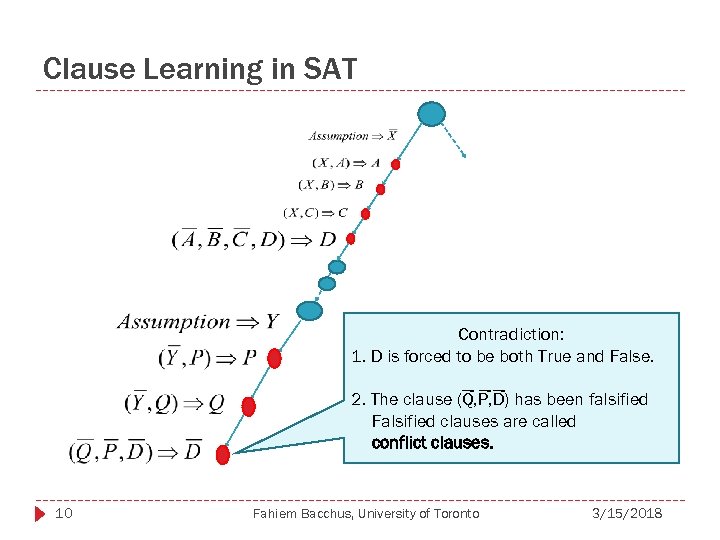
Clause Learning in SAT Contradiction: 1. D is forced to be both True and False. 2. The clause (Q, P, D) has been falsified Falsified clauses are called conflict clauses. 10 Fahiem Bacchus, University of Toronto 3/15/2018
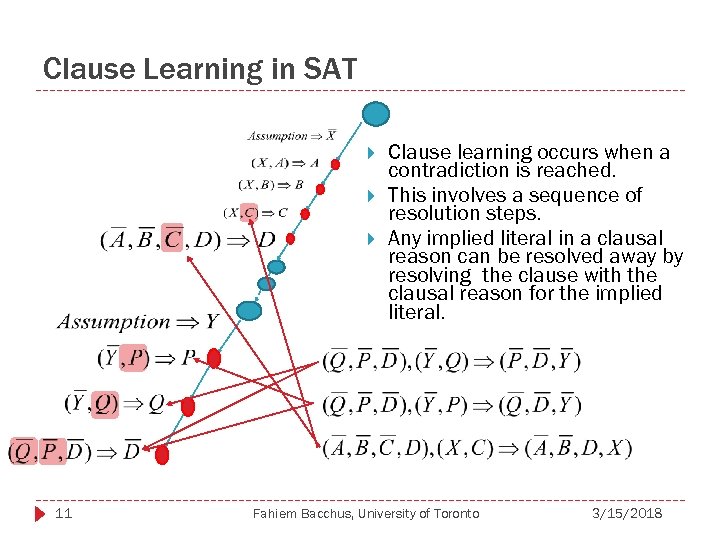
Clause Learning in SAT 11 Clause learning occurs when a contradiction is reached. This involves a sequence of resolution steps. Any implied literal in a clausal reason can be resolved away by resolving the clause with the clausal reason for the implied literal. Fahiem Bacchus, University of Toronto 3/15/2018
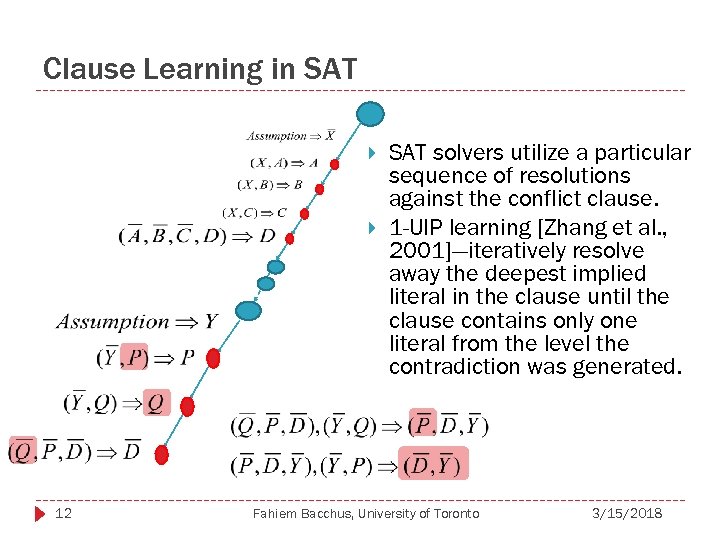
Clause Learning in SAT 12 SAT solvers utilize a particular sequence of resolutions against the conflict clause. 1 -UIP learning [Zhang et al. , 2001]—iteratively resolve away the deepest implied literal in the clause until the clause contains only one literal from the level the contradiction was generated. Fahiem Bacchus, University of Toronto 3/15/2018
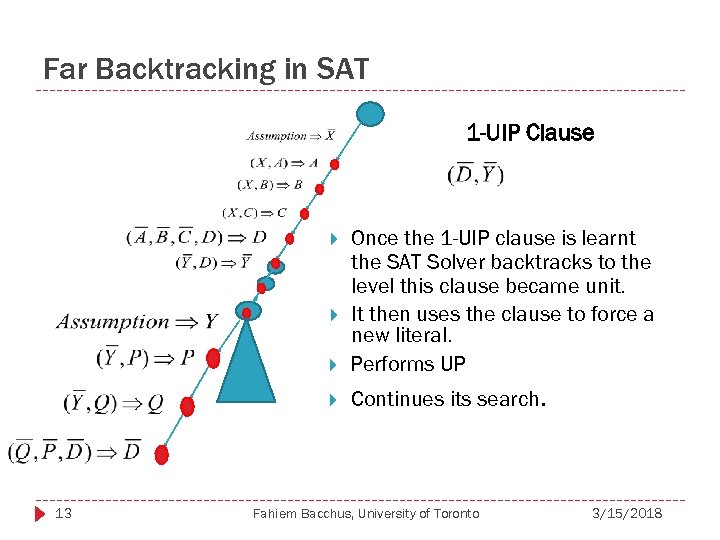
Far Backtracking in SAT 1 -UIP Clause Once the 1 -UIP clause is learnt the SAT Solver backtracks to the level this clause became unit. It then uses the clause to force a new literal. Performs UP Continues its search. 13 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning The power of clause learning has been examined from the point of view of theory of proof complexity [Cook & Reckhow 1977]. This area looks at the question of how large proofs can become and their relative sizes in in different propositional proof systems. DPLL with Clause learning performing resolution (a particular type or resolution). Various restricted versions of resolution have been well studied. [Buresh-Oppenhiem, Pitassi 2003] contains a nice review of previous results and a number of new results in this area. 14 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning Every DPLL search tree refuting an UNSAT instance contains a TREE-Resolution proofs can be exponentially larger than REGULAR-Resolutions proofs can be exponentially larger than general (unrestricted) resolution proofs. UNSAT formulas min_size(DPLL Search Tree) ≥ min_size(TREE-Resolution) >> min_size(REGULAR-Resolution) >> min_size(general resolution) 15 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning Furthermore every TREE-Resolution proof is a REGULARResolution proof and every REGULAR-Resolution proof is a general resolution proof. UNSAT formulas min_size(DPLL Search Tree) ≥ min_size(TREE-Resolution) ≥ min_size(REGULAR-Resolution) ≥ min_size(general resolution) 16 Fahiem Bacchus, University of Toronto 3/15/2018
![Theoretical Power of Clause Learning [Beame, Kautz, and Sabharwal 2003] showed that clause learning](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-17.jpg "Theoretical Power of Clause Learning [Beame, Kautz, and Sabharwal 2003] showed that clause learning")
Theoretical Power of Clause Learning [Beame, Kautz, and Sabharwal 2003] showed that clause learning can SOMETIMES yield exponentially smaller proofs than REGULAR. Unknown if general resoution proofs are some times smaller. UNSAT formulas min_size(DPLL Search Tree) ≥ min_size(TREE-Resolution) >> min_size(REGULAR-Resolution) >> min_size(Clause Learning DPLL Search Tree) ≥ min_size(general resolution) 17 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning It is still unknown if REGULAR or even TREE resolutions can sometimes be smaller than the smallest Clause Learning DPLL Search tree. 18 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning It is also easily observed [Beame, Kautz, and Sabharwal 2003] that with restarts clause learning can make the DPLL Search Tree as small as the smallest general resolution proof on any formula. UNSAT formulas min_size(Clause Learning + Restarts DPLL Search Tree) = min_size(general resolution) 19 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning In sum. Clause Learning, especially with restarts, has the potential to yield exponential reductions in the size of the DPLL search tree. With clause learning DPLL can potentially solve problems exponentially faster. That this can happen in practice has been irrefutably demonstrated by modern SAT solvers. 20 Modern SAT solvers have been able to exploit theoretical potential of clause learning. Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Power of Clause Learning The theoretical advantages of clause learning also hold for CSP backtracking search So the question that arises is can theoretical potential of clause learning also be exploited in CSP solvers. 21 Fahiem Bacchus, University of Toronto 3/15/2018
1. 1 Clause Learning in CSPs 22 Fahiem Bacchus, University of Toronto 3/15/2018
Clause Learning in CSPs Joint work with George Katsirelos who just completed his Ph. D with me “No. Good Processing in CSPs” Learning has been used in CSPs, but have not had the kind of impact Clause Learning has had in SAT. [Decther 1990; T. Schiex & G. Verfaillie 1993; Frost & Dechter 1994; Jussien & Barichard 2000] This work has investigated No. Good learning. A No. Good is a set of variable assignments that cannot be extended to a solution. 23 Fahiem Bacchus, University of Toronto 3/15/2018
No. Good Learning is NOT Clause Learning. It is strictly less powerful. To illustrate this let us consider encoding a CSP as a SAT problem, and compare what Clause Learning will do on the SAT encoding to what No. Good Learning would do. 24 Fahiem Bacchus, University of Toronto 3/15/2018
Propositional Encoding of a CSP—the propositions. A CSP consists of a Set of variables Vi and constraints Cj Each variable has a domain of values Dom[Vi] = {d 1, …, dm}. Consider the set of propositions Vi=dj one for each value of each variable. Vi=dj means that Vi has been assigned the value dj. ¬(Vi=dj) means that Vi has not been assigned the value dj True when the assignment has been made. True when dj has been pruned from Vi’s domain. if Vi has been assigned a different value, all other values (including dj) are pruned from its domain. Usually write Vi≠dj instead of ¬(Vi=dj). We encode the CSP using clauses over these assignment propositions. 25 Fahiem Bacchus, University of Toronto 3/15/2018
![Propositional Encoding of a CSP—the clauses. For each variable V with Dom[V]={d 1, …,](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-26.jpg "Propositional Encoding of a CSP—the clauses. For each variable V with Dom[V]={d 1, …,")
Propositional Encoding of a CSP—the clauses. For each variable V with Dom[V]={d 1, …, dk} we have the following clauses: For each constraint C(X 1, …, Xk) over some set of variables we have the following clauses: (V=d 1, V=d 2, …, V=dk) (must have a value) For every pair of values (di, dk) the clause (V ≠ di, V ≠ dk) (has a unique value) For each assignment to its variables that falsifies the constraint we have a clause blocking that assignment. If C(a, b, …, k) = FALSE then we have the clause (X 1 ≠ a, X 2 ≠ b, …, Xk ≠ k) This is the direct encoding of [Walsh 2000]. 26 Fahiem Bacchus, University of Toronto 3/15/2018
DPLL on this Encoded CSP. Unit Propagation on this encoding is essentially equivalent to Forward Checking on the original CSP. 27 Fahiem Bacchus, University of Toronto 3/15/2018
![DPLL on the encoded CSP Variables Q, X, Y, Z, . . . Dom[Q]](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-28.jpg "DPLL on the encoded CSP Variables Q, X, Y, Z, . . . Dom[Q]")
DPLL on the encoded CSP Variables Q, X, Y, Z, . . . Dom[Q] = {0, 1} Dom[X, Y, Z] = {1, 2, 3} Constraints Q+X+Y≥ 3 Q+X+Z≥ 3 Q+Y+Z≤ 3 28 Fahiem Bacchus, University of Toronto 3/15/2018
DPLL on the encoded CSP Clause learning 29 Fahiem Bacchus, University of Toronto 3/15/2018
DPLL on the encoded CSP Clause learning A 1 -UIP Clause 30 Fahiem Bacchus, University of Toronto 3/15/2018
DPLL on the encoded CSP This clause is not a No. Good! It asserts that we cannot have Q = 0, Y = 2, and Z ≠ 1 simultaneously. This is a set of assignments and domain prunings that cannot lead to a solution. A No. Good is only a set of assignments. To obtain a No. Good we have to further resolve away Z = 1 from the clause. 31 Fahiem Bacchus, University of Toronto 3/15/2018
DPLL on the encoded CSP No. Good learning This clause is a No. Good. It says that we cannot have the set of assignments Q = 0, X = 1, Y = 2 No. Good learning requires resolving the conflicts back to the decision literals. 32 Fahiem Bacchus, University of Toronto 3/15/2018
No. Goods vs. Clauses (Generalized No. Goods) Unit propagation over a collection of learnt No. Goods is ineffective. 1. Nogoods are clauses containing negated literals only, e. g. , (Z ≠ 1, Y ≠ 0, X ≠ 3). If one of these clauses becomes unit, e. g. , (X ≠ 3), the forced literal can only satisfy other No. Good clauses, it can never reduce the length of those clauses. A single clause can represent an exponential number of No. Goods 2. 33 (Q ≠ 1, Z = 1, Y = 1) is equivalent to (Domain = {1, 2, 3}) (Q ≠ 1, Z ≠ 2, Y ≠ 2) (Q ≠ 1, Z ≠ 3, Y ≠ 2) (Q ≠ 1, Z ≠ 2, Y ≠ 3) (Q ≠ 1, Z ≠ 3, Y ≠ 3) Fahiem Bacchus, University of Toronto 3/15/2018
No. Goods vs. Clauses (Generalized No. Goods) 3. 4. 34 The 1 -UIP clause can prune more branches during the future search than the No. Good clause [Katsirelos 2007]. Clause Learning can yield super-polynomially smaller search trees than No. Good Learning [Katsirelos 2007] Fahiem Bacchus, University of Toronto 3/15/2018
Encoding to SAT With all of these benefits of clause learning over No. Good learning the natural question is Why not encode CSPs to SAT and immediately obtain the benefits of Clause Learning already implemented in modern SAT solvers? 35 Fahiem Bacchus, University of Toronto 3/15/2018
Encoding to SAT The SAT theory produced by the direct encoding is not very effective. 1. Unit Prop. on this encoding only achieves Forward Checking (a weak form of propagation). Under the direct encoding constraints of arity k yield 2 O(k) clauses. Hence the resultant SAT theory is too large. No direct way of exploiting propagators. 2. 3. 36 Specialized polynomial time algorithms for doing propagation on constraints of large arity. Fahiem Bacchus, University of Toronto 3/15/2018
Encoding to SAT Some of these issues can be address by better encodings, e. g. , [Bacchus 2007, Katsirelos & Walsh 2007, Quimper & Walsh 2007]. But overall complete conversion to SAT is currently impractical. 37 Fahiem Bacchus, University of Toronto 3/15/2018
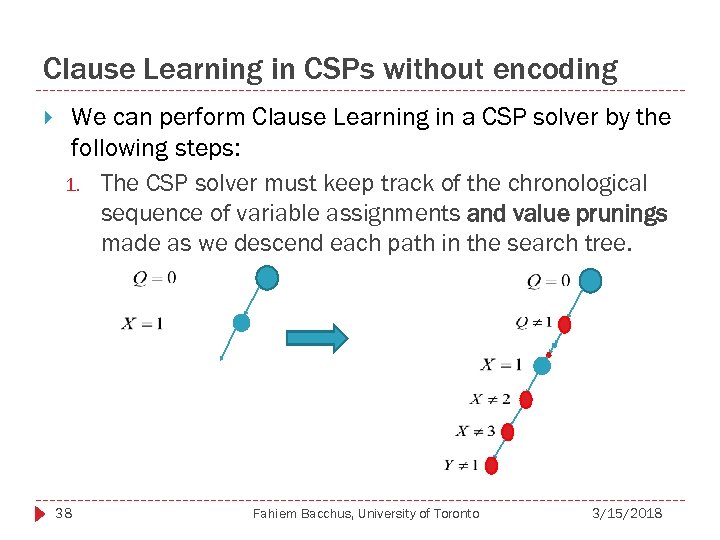
Clause Learning in CSPs without encoding We can perform Clause Learning in a CSP solver by the following steps: 1. The CSP solver must keep track of the chronological sequence of variable assignments and value prunings made as we descend each path in the search tree. 38 Fahiem Bacchus, University of Toronto 3/15/2018
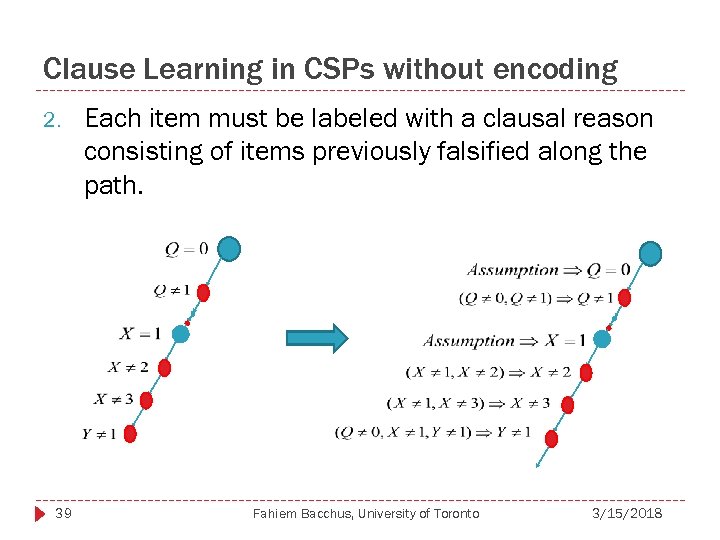
Clause Learning in CSPs without encoding 2. 39 Each item must be labeled with a clausal reason consisting of items previously falsified along the path. Fahiem Bacchus, University of Toronto 3/15/2018
Clause Learning in CSPs without encoding 3. Contradictions are labeled by falsified clauses, e. g. , Domain Wipe Outs can be labeled by the must have a value clause. From this information clause learning can be performed whenever a contradiction is reached. These clauses can be stored in a clausal database Unit Propagation can be run on this database as new value assignments or value prunings are preformed. 40 The inferences of Unit Propagation agument the other constraint propagation done by the CSP solver. Fahiem Bacchus, University of Toronto 3/15/2018
Higher Levels of Local Consistency Note that this technique works irrespective of kinds of inference performed during search. That is, we can use any kind of inference we want to infer a new value pruning or new variable assignment—as long as we can label the inference with a clausal reason. This raises the question of how do we generate clausal reasons for other forms inference. [Katsirelos 2007] answers this question for the most commonly used form of inference: Generalized Arc Consistency. 41 Including ways of obtain clausal reasons from various types of GAC propagators, ALL-DIFF, GCC. Fahiem Bacchus, University of Toronto 3/15/2018
![Some Empirical Data [Katsirelos 2007] GAC with No. Good learning helps a bit. GAC](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-42.jpg "Some Empirical Data [Katsirelos 2007] GAC with No. Good learning helps a bit. GAC")
Some Empirical Data [Katsirelos 2007] GAC with No. Good learning helps a bit. GAC with clause learning but where GAC labels it inferences with No. Goods offers only minor improvements. To get significant improvements must do clause learning as well have proper clausal reasons from GAC. 42 Fahiem Bacchus, University of Toronto 3/15/2018
Observations Caching techniques have great potential, but to make them effective in practice it can sometimes require resolving a number of different issues. This work goes a long ways towards achieving the goal of exploiting theoretical potential of Clause Learning. Prediction: Clause learning will play a fundamental role in the next generation of CSP solvers, and these solvers will often be orders of magnitude more effective than current solvers. 43 Fahiem Bacchus, University of Toronto 3/15/2018
Open Issues Many issues remain open. Here we mention only one: Restarts. As previously pointed out, clause learning gains a great deal more power with restarts. With restarts it can be as powerful as unrestricted resolution. Restarts play an essential role in the performance of SAT solvers. Both full restarts and partial restarts. 44 Fahiem Bacchus, University of Toronto 3/15/2018
Search vs. Inference With restarts and clause learning, the distinction of search vs. inference is turned on its head. Instead the distinction becomes systematic vs. opportunistic inference. Now search is performing inference. Enforcing a high level of consistency during search is performing systematic inference. Searching until we learn a good clause is opportunistic. Sat solvers perform very little systematic inference, only Unit Propagation, but they perform lots of opportunistic inference. CSP solvers essentially do the opposite. 45 Fahiem Bacchus, University of Toronto 3/15/2018
One Open Question In SAT solvers opportunistic inference is feasible: if a learnt clause turns out not to be useful it doesn’t matter much as the search to learn that clause did not take much time. Search (nodes/second rate) is very fast. In CSP solvers the enforcement of higher levels of local consistency makes restarts and opportunistic inference very expensive. Search (nodes/second rate) is very slow. Is high levels of consistency really the most effective approach for solving CSP once Clause learning is available? 46 Fahiem Bacchus, University of Toronto 3/15/2018
2. 47 Formula Caching when considering all solutions. Fahiem Bacchus, University of Toronto 3/15/2018
Considering All Solutions? One such class of problems are those that can be expressed as Sum-Of-Product problems [Decther 1999]. 1. Finite Set of Variables, V 1, V 2, …, Vn 2. A finite domain of values for each variable Dom[Vi]. 3. A finite set of real valued local functions f 1, f 2, …, fm. 48 Each function is local in the sense that it only depends on a subset of the variables. f 1(V 1, V 2), f 2(V 2, V 4, V 6), … The locality of the functions can be exploited algorithmically. Fahiem Bacchus, University of Toronto 3/15/2018
Sum of Products The sum of products problem is to compute from this representation The local functions assign a value to every complete instantiation of the variables (the product) and we want to compute some amalgamation of these values A number of different problems can be cast as instances of sum-of-product [Decther 1999]. 49 Fahiem Bacchus, University of Toronto 3/15/2018
Sum of Products—Examples #CSPs count the number of solutions. Inference in Bayes Nets. Optimization: the functions are sub-objective functions returning real values and the global objective is to maximize the sum of the sub-objects (cf. soft constraints, generalized additive utility). 50 Fahiem Bacchus, University of Toronto 3/15/2018
![Algorithms Brief History [Arnborg et al. 1988] It had long been noted that various](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-51.jpg "Algorithms Brief History [Arnborg et al. 1988] It had long been noted that various")
Algorithms Brief History [Arnborg et al. 1988] It had long been noted that various NP-Complete problems on graphs were easy on Trees. With the characterization of NP completeness systematic study of how to extend these techniques beyond trees started in the 1970 s A number of Dynamic Programming algorithms were developed for partial K-trees which could solve many hard problem in time linear in the size of the graph (but exponential in K) 51 Fahiem Bacchus, University of Toronto 3/15/2018
![Algorithms Brief History [Arnborg et al. 1988] These ideas were made systematic by Robertson](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-52.jpg "Algorithms Brief History [Arnborg et al. 1988] These ideas were made systematic by Robertson")
Algorithms Brief History [Arnborg et al. 1988] These ideas were made systematic by Robertson & Seymour who wrote a series of 20 articles to prove Wagner’s conjecture [1983]. Along the way they defined the concept of Tree and Branch decompositions and the graph parameters Tree. Width and Branch-Width. It was subsequently noted that partial k-Trees are equivalent to the class of graphs with tree width ≤ k. So all of the dynamic programming algorithms developed for partial K-Trees worked for tree width k graphs. The notion of tree width has been exploited many areas of computer science and combinatorics & optimization. . 52 Fahiem Bacchus, University of Toronto 3/15/2018
Three types of Algorithms These algorithms all take one of three basic forms all of which achieve the same kinds of tree-width complexity guarantees. To understand these forms we first introduce the notion of a branch decomposition (which is somewhat easier to utilize than treedecompositions when dealing the local functions with arity greater than 2) 53 Fahiem Bacchus, University of Toronto 3/15/2018
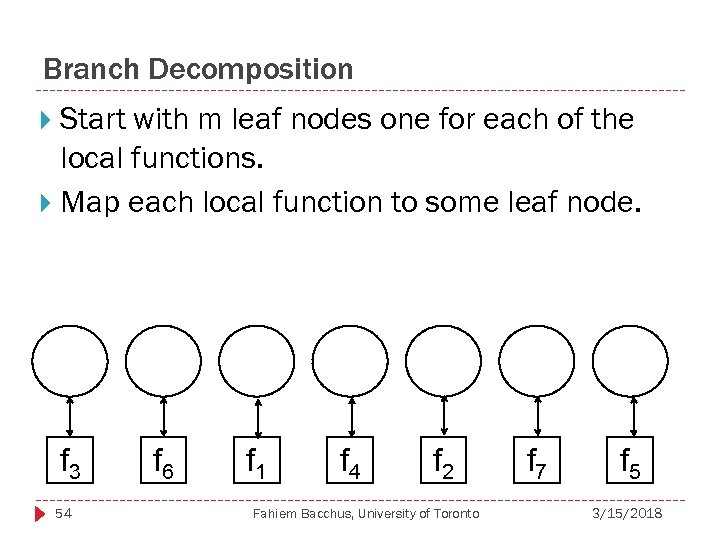
Branch Decomposition Start with m leaf nodes one for each of the local functions. Map each local function to some leaf node. f 3 54 f 6 f 1 f 4 f 2 Fahiem Bacchus, University of Toronto f 7 f 5 3/15/2018
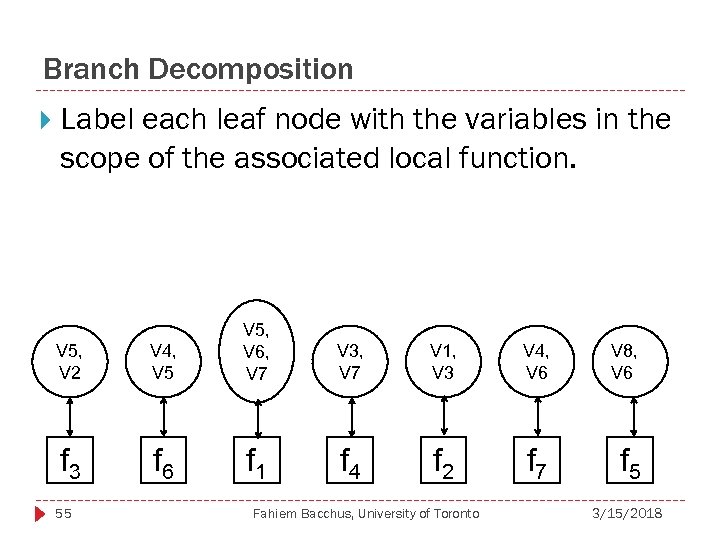
Branch Decomposition Label each leaf node with the variables in the scope of the associated local function. V 5, V 2 V 4, V 5, V 6, V 7 f 3 f 6 f 1 55 V 3, V 7 V 1, V 3 V 4, V 6 V 8, V 6 f 4 f 2 f 7 f 5 Fahiem Bacchus, University of Toronto 3/15/2018
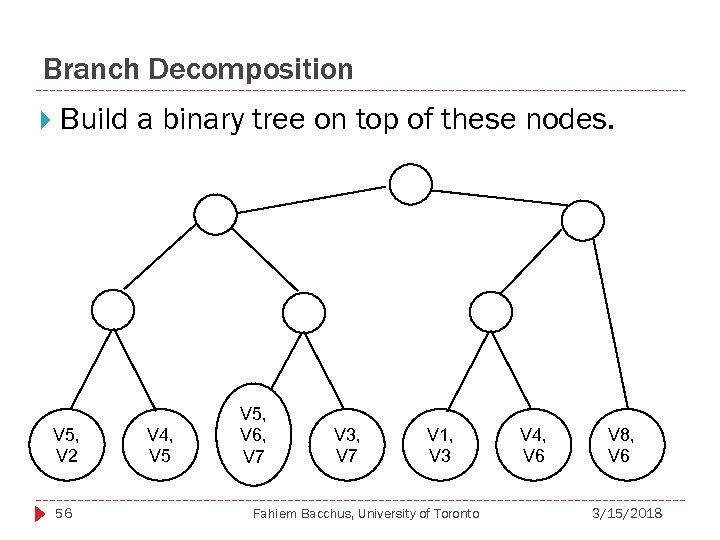
Branch Decomposition Build a binary tree on top of these nodes. V 5, V 2 56 V 4, V 5, V 6, V 7 V 3, V 7 V 1, V 3 Fahiem Bacchus, University of Toronto V 4, V 6 V 8, V 6 3/15/2018
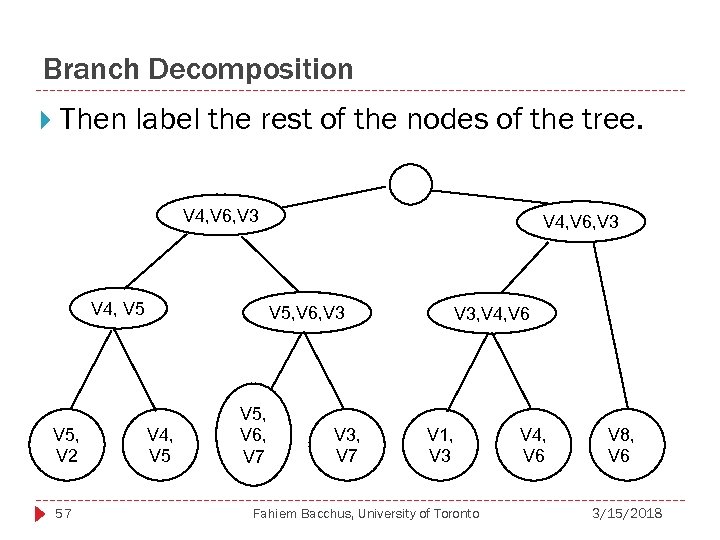
Branch Decomposition Then label the rest of the nodes of the tree. V 4, V 6, V 3 V 4, V 5, V 2 57 V 4, V 6, V 3 V 5, V 6, V 3 V 4, V 5, V 6, V 7 V 3, V 4, V 6 V 1, V 3 Fahiem Bacchus, University of Toronto V 4, V 6 V 8, V 6 3/15/2018
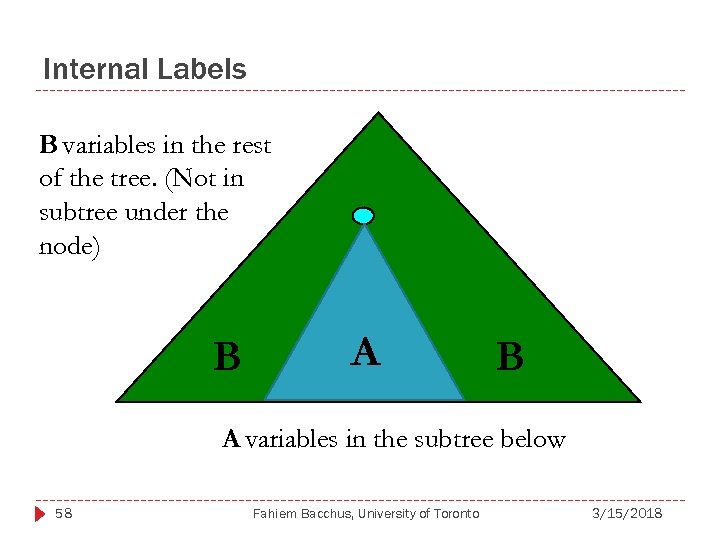
Internal Labels B variables in the rest of the tree. (Not in subtree under the node) B A variables in the subtree below 58 Fahiem Bacchus, University of Toronto 3/15/2018
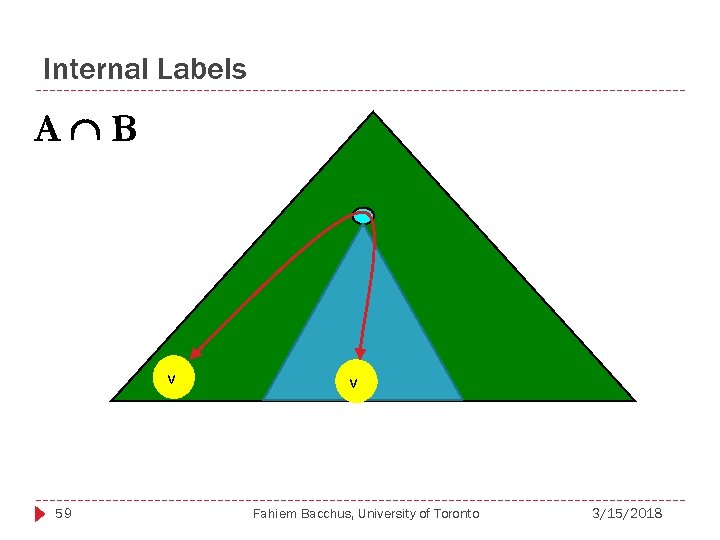
Internal Labels A B v 59 v Fahiem Bacchus, University of Toronto 3/15/2018
Branch Width of a particular decomposition is the size of the minimal label. Branch width is the minimal width over all possible branch decompositions. Branch width is no more than the tree-width. 60 Fahiem Bacchus, University of Toronto 3/15/2018
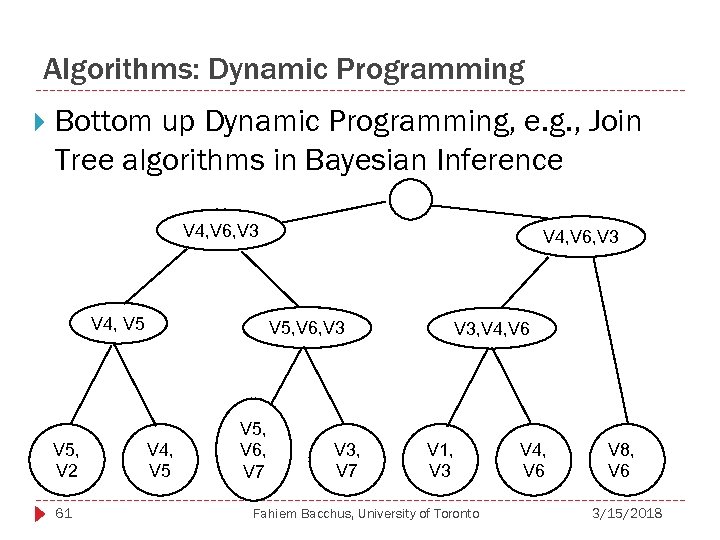
Algorithms: Dynamic Programming Bottom up Dynamic Programming, e. g. , Join Tree algorithms in Bayesian Inference V 4, V 6, V 3 V 4, V 5, V 2 61 V 4, V 6, V 3 V 5, V 6, V 3 V 4, V 5, V 6, V 7 V 3, V 4, V 6 V 1, V 3 Fahiem Bacchus, University of Toronto V 4, V 6 V 8, V 6 3/15/2018
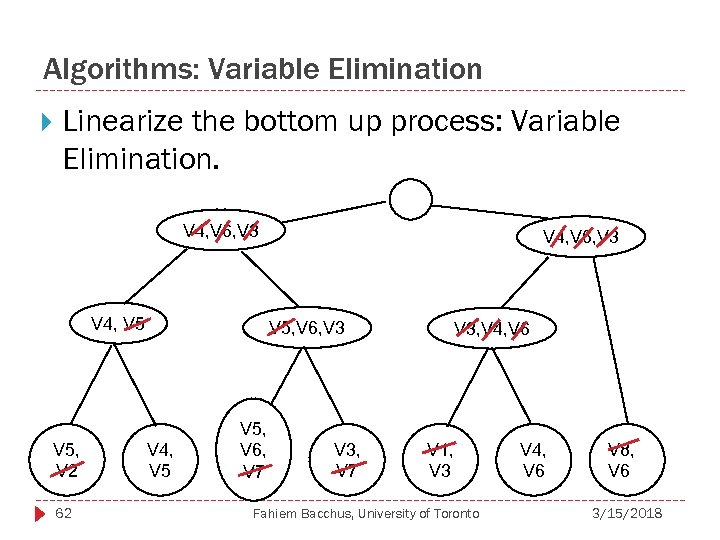
Algorithms: Variable Elimination Linearize the bottom up process: Variable Elimination. V 4, V 6, V 3 V 4, V 5, V 2 62 V 4, V 6, V 3 V 5, V 6, V 3 V 4, V 5, V 6, V 7 V 3, V 4, V 6 V 1, V 3 Fahiem Bacchus, University of Toronto V 4, V 6 V 8, V 6 3/15/2018
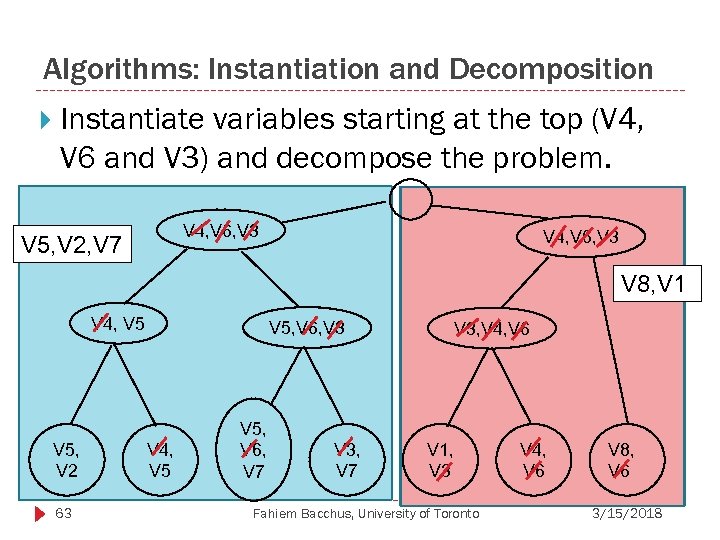
Algorithms: Instantiation and Decomposition Instantiate variables starting at the top (V 4, V 6 and V 3) and decompose the problem. V 4, V 6, V 3 V 5, V 2, V 7 V 4, V 6, V 3 V 8, V 1 V 4, V 5, V 2 63 V 5, V 6, V 3 V 4, V 5, V 6, V 7 V 3, V 4, V 6 V 1, V 3 Fahiem Bacchus, University of Toronto V 4, V 6 V 8, V 6 3/15/2018
Instantiation and Decomposition A number of works have used this approach 64 Pseudo Tree Search [Freuder & Quinn 1985] Counting Solutions [Bayardo & Pehoushek 2000] Recursive Conditioning [Darwiche 2001] Tour Merging [Cook & Seymour 2003] AND-OR Search [Dechter & Mateescu 2004] … Fahiem Bacchus, University of Toronto 3/15/2018
Instantiation and Decomposition Solved by AND/OR search: as we instantiate variables we examine the residual subproblem. If the sub-problem consists of disjoint parts that share no variables (components) we solve each component in a separate recursion. 65 Fahiem Bacchus, University of Toronto 3/15/2018
Theoretical Results With the right ordering this approach can solve the problem in time 2 O(w log n) and linear space, were w is the branch (tree) width of the instance. If the solved components are cached so that they do not have to be solved again the approach can solve the problem in time n. O(1)2 O(w). But now we need n. O(1)2 O(w) space. 66 Fahiem Bacchus, University of Toronto 3/15/2018
Solving Sum-Of-Products with Backtracking In joint work with Toniann Pitassi & Shannon Dalmao we showed that caching is in fact sufficient to achieve these bounds with standard backtracking search. [Bacchus, et al. 2003] 67 AND/OR decomposition of the search tree is not necessary (and may be harmful). Instead an ordinary decision tree can be searched. Once again Caching again provides a significant increase in theoretical power of backtracking. Fahiem Bacchus, University of Toronto 3/15/2018
Simple Formula Caching As assumptions are made during search the problem is reduced. In Simple Formula Caching we cache every solved residual formula, and if we encounter the same residual formula again we utilize its cached value instead of solving the same sub-problem again. Two residual formulas are the same if 68 They contain the same (unassigned) variables. All instantiated variables in the remaining constraints (constraints with at least one unassigned variable) are instantiated to the same value. Fahiem Bacchus, University of Toronto 3/15/2018
![Simple Formula Caching C 1(X, Y), C 2(Y, Z) C 3(Y, Q) [X=a, Y=b]](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-69.jpg "Simple Formula Caching C 1(X, Y), C 2(Y, Z) C 3(Y, Q) [X=a, Y=b]")
Simple Formula Caching C 1(X, Y), C 2(Y, Z) C 3(Y, Q) [X=a, Y=b] C 2(Y=b, Z) C 3(Y=b, Q) C 1(X, Y), C 2(Y, Z) C 3(Y, Q) [X=b, Y=b] C 2(Y=b, Z) C 3(Y=b, Q) These residual formulas are the same even though we obtained them from different instantiations. 69 Fahiem Bacchus, University of Toronto 3/15/2018
Simple Formula Caching BTSimple. Cache(Φ) if In. Cache(Φ), return Cached. Value(Φ) else Pick a variable V in Φ, value = 0 for d in Domain[V] value = value + BTSimple. Cache(Φ|V=d) Add. To. Cache(Φ, value) return Runs in time and space 2 O(w log n) 70 Fahiem Bacchus, University of Toronto 3/15/2018
Component Caching We can achieve the same performance as AND/OR decomposition, i. e. , 2 O(w log n) time with linear space or n. O(1)2 O(w) time with n. O(1)2 O(w) space by examining the residual formula for disjoint Components. We cache these disjoint components as they are solved. We remove any solved component from the residual formula. 71 Fahiem Bacchus, University of Toronto 3/15/2018
Component Caching Since components are no longer solved in a separate recursion we have to be a bit cleverer about identifying the value of these components from the search computation. This can be accomplished by using the cache in a clever way, or by dependency tracking techniques. 72 Fahiem Bacchus, University of Toronto 3/15/2018
Component Caching There are some potential advantages of searching a single tree rather than and AND/OR tree. 73 With an AND/OR tree one has to make a commitment to which component to solve first. The wrong decision when doing Bayesian Inference or optimization with Branch and Bound can be expensive In the single tree the components are solved in an interleaved manner. This also provides more flexibility with respect to variable ordering. Fahiem Bacchus, University of Toronto 3/15/2018
Bayesian Inference via Backtracking Search These ideas were used to build a fairly successful Bayes Net Reasoner. [Bacchus et al. 2003]. Better performance however would require exploiting more of the structure internal to the local functions. 74 Fahiem Bacchus, University of Toronto 3/15/2018
Exploiting Micro Structure C 1(A, Y, Z) = TRUE A=0 Y = 1 A = 1 Y=0 & Z = 1 Then C(A=0, Y, Z) is in fact not a function of Z. That is C(A=0, Y, Z) C(A=0, Y) C 2(X, Y, Z) = TRUE X+Y+Z≥ 3 Then C(X=3, Y, Z) is already satisfied. 75 Fahiem Bacchus, University of Toronto 3/15/2018
Exploiting Micro Structure In both cases if we could detect this during search we could potentially 76 Generate more components, e. g. , if we could reduce C 1(A=0, Y, Z) to a C 1(A=0, Y) perhaps Y and Z would be in different components. Generate more cache hits, e. g. , if the residual formula differs from a cached formula only because it contains C 2(X=3, Y, Z), recognizing that constraint is already satisfied would allow us to ignore it and generate the cache hit. Fahiem Bacchus, University of Toronto 3/15/2018
Exploiting Micro Structure It is interesting to note that if we encode to CNF we do get to exploit more of the micro structure (structure internal to the constraint). Clauses with a true literal are satisfied and can be removed from the residual formula. Bayes Net Reasoners using CNF encodings have displayed very good performance [Chavira & Darwiche 2005]. 77 Fahiem Bacchus, University of Toronto 3/15/2018
Exploiting Micro Structure Unfortunately, as pointed out before, encoding in CNF can result in an impractical blowup in the size of the problem representation. Practical techniques for exploiting the micro structure remain a promising area for further research. 78 Some promising results by Kitching to detect when a symmetric version of a current component has already been solved [Kitching & Bacchus 2007], but more work to be done. Fahiem Bacchus, University of Toronto 3/15/2018
Observations Component caching solvers are the most effective ways of exactly computing the number of solutions of a SAT formula. Allow solution of certain types of Bayesian Inference problems not solvable by other methods. Have shown promise in solving decomposable optimization problems [Dechter & Marinescu 2005, de Givry et al. 2006, Kitching & Bacchus 2007] To date all these works have used AND/OR search. So exploiting the advantages of plain backtracking search remains work to be done [Kitching in progress]. Better exploiting micro structure also remains work to be done. 79 Fahiem Bacchus, University of Toronto 3/15/2018
Conclusions Caching is a technique that has great potential for making a material difference in the effectiveness of backtracking search. The range of practical mechanisms for exploiting caching remains a very fertile area for future research. Research in this direction might well change present day “accepted practice” in constraint solving. 80 Fahiem Bacchus, University of Toronto 3/15/2018
![References [Marques-Silva and Sakallah, 1996] J. P. Marques-Silva and K. A. Sakallah. Grasp—a new](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-81.jpg "References [Marques-Silva and Sakallah, 1996] J. P. Marques-Silva and K. A. Sakallah. Grasp—a new")
References [Marques-Silva and Sakallah, 1996] J. P. Marques-Silva and K. A. Sakallah. Grasp—a new search algorithm for Satisfiability. In ICCAD, 220 -227, 1996. [Zhang et al. , 2001] L. Zhang, C. F. Madigan, M. H. Moskewicz, and S. Malik. Efficient conflict driven learning in a Boolean Satisfiability solver. In ICCAD, 279 -285, 2001. [Cook & Reckhow 1977] [Buresh-Oppenhiem, Pitassi 2003] P. Beame, H. Kautz, and A. Sabharwal: Towards Understanding and Harnessing the Potential of Clause Learning. J. Artif. Intell. Res. (JAIR) 22: 319 -351 (2004) [Decther 1990] J. Buresh-Oppenheim and T. Pitassi, The Complexity of Resolution Refinements, in Proceedings of the 18 th IEEE Symposium on Logic in Computer Science (LICS), June 2003, pp. 138 -147 [Beame, Kautz, and Sabharwal 2003] S. A. Cook and R. A. Reck-how, The relative efficiency of propositional proof systems, J. Symb. Logic, 44 (1977), 36 -50. R. Dechter: Enhancement Schemes for Constraint Processing: Backjumping, Learning, and Cutset Decomposition. Artif. Intell. 41(3): 273 -312 (1990) [T. Schiex & G. Verfaillie 1993] 81 T. Schiex and G. Verfaillie. Nogood recording for static and dynamic CSP. Proceeding of the 5 th IEEE International Conference on Tools with Artificial Intelligence (ICTAI'93), p. 48 -55, Boston, MA, november 1993. Fahiem Bacchus, University of Toronto 3/15/2018
![References [Frost & Dechter 1994] D. Frost, R. Dechter: Dead-End Driven Learning. AAAI 1994:](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-82.jpg "References [Frost & Dechter 1994] D. Frost, R. Dechter: Dead-End Driven Learning. AAAI 1994:")
References [Frost & Dechter 1994] D. Frost, R. Dechter: Dead-End Driven Learning. AAAI 1994: 294 -300 [Jussien & Barichard 2000] N. Jussien, V. Barichard "The Pa. LM system: explanation-based constraint programming" , Proceedings of TRICS: Techniques fo. R Implementing Constraint programming Systems, a post-conference workshop of CP 2000, pp. 118133, 2000 [Walsh 2000] T. Walsh. SAT v CSP, Proceedings of CP-2000, pages 441 -456, Springer-Verlag LNCS-1894, 2000. [Katsirelos 2007] G. Katsirelos, No. Good Processing in CSPs. Ph. D thesis. Department of Computer Science, University of Toronto. [Bacchus 2007] F. Bacchus. GAC via Unit Propagation. International Conference on Principles and Practice of Constraint Programming (CP 2007) , pages 133 -147. [Katsirelos & Walsh 2007] G. Katsirelos and T. Walsh. A Compression Algorithm for Large Arity Extensional Constraints. . Proceedings of CP 2007, LNCS 4741, 2007. [Quimper & Walsh 2007] C. Quimper and T. Walsh. Decomposing Global Grammar Constraints. Proceedings of CP-2007, LNCS 4741, 590 -604 2007. [Decther 1999] R. Decther. "Bucket Elimination: A unifying framework for Reasoning. " In "Artificial Intelligence", October, 1999. 82 Fahiem Bacchus, University of Toronto 3/15/2018
![References [de Givry et al. 2006] 83 S. de Givry, T. Schiex, G. Verfaillie.](https://present5.com/presentation/a888302a94fa2dde8edbfe7b2d189b0f/image-83.jpg "References [de Givry et al. 2006] 83 S. de Givry, T. Schiex, G. Verfaillie.")
References [de Givry et al. 2006] 83 S. de Givry, T. Schiex, G. Verfaillie. Exploiting Tree Decomposition and Soft Local Consistency in Weighted CSP. Proc. of AAAI'2006. Boston (MA), USA. Fahiem Bacchus, University of Toronto 3/15/2018
Скачать презентацию Caching in Backtracking Search Fahiem Bacchus University of
a888302a94fa2dde8edbfe7b2d189b0f.ppt