d535d328f2f37c6d928438cf010d8adb.ppt
- Количество слайдов: 42

Business Statistics: A Decision-Making Approach 6 th Edition Chapter 8 Introduction to Hypothesis Testing Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Chap 8 -1

Chapter Goals After completing this chapter, you should be able to: n Formulate null and alternative hypotheses for applications involving a single population mean n Formulate a decision rule for testing a hypothesis n Know how to use the test statistic, critical value, and pvalue approaches to test the null hypothesis n Know what Type I and Type II errors are n Compute the probability of a Type II error Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 2

What is a Hypothesis? n A hypothesis is a claim (assumption) about a population parameter: n population mean Example: The mean monthly cell phone bill of this city is = $42 n population proportion Example: The proportion of adults in this city with cell phones is p =. 68 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 3

The Null Hypothesis, H 0 n States the assumption (numerical) to be tested Example: The average number of TV sets in U. S. Homes is at least three ( ) n Is always about a population parameter, not about a sample statistic Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 4

The Null Hypothesis, H 0 n n (continued) Begin with the assumption that the null hypothesis is true n Similar to the notion of innocent until proven guilty Refers to the status quo Always contains “=” , “≤” or “ ” sign May or may not be rejected Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 5

The Alternative Hypothesis, HA n Is the opposite of the null hypothesis n n n e. g. : The average number of TV sets in U. S. homes is less than 3 ( HA: < 3 ) Challenges the status quo Never contains the “=” , “≤” or “ ” sign May or may not be accepted Is generally the hypothesis that is believed (or needs to be supported) by the researcher Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 6
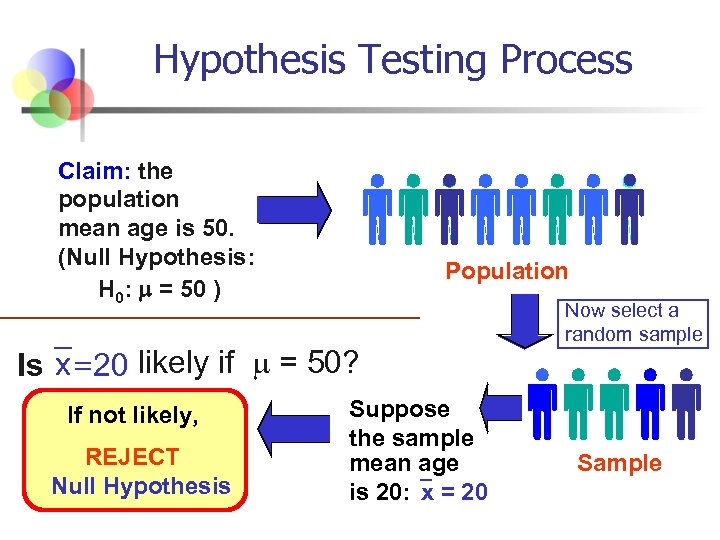
Hypothesis Testing Process Claim: the population mean age is 50. (Null Hypothesis: H 0: = 50 ) Population Is x = 20 likely if = 50? If not likely, REJECT Null Hypothesis Suppose the sample mean age is 20: x = 20 Now select a random sample Sample
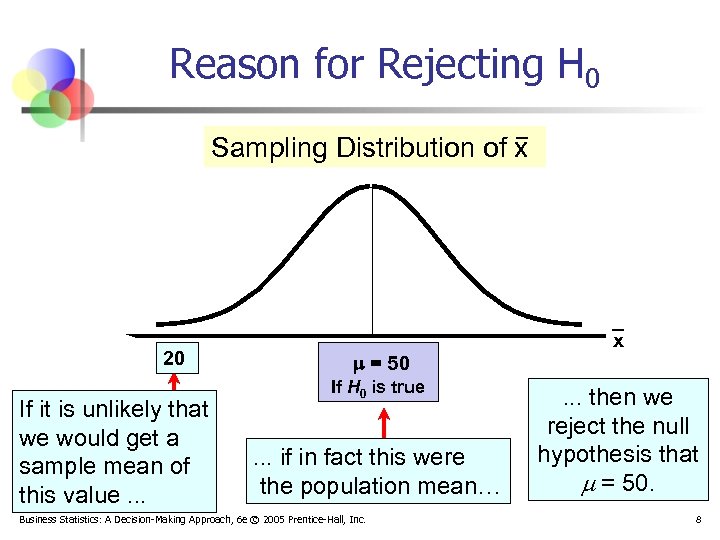
Reason for Rejecting H 0 Sampling Distribution of x 20 If it is unlikely that we would get a sample mean of this value. . . = 50 If H 0 is true . . . if in fact this were the population mean… Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. x . . . then we reject the null hypothesis that = 50. 8

Level of Significance, n Defines unlikely values of sample statistic if null hypothesis is true n n Defines rejection region of the sampling distribution Is designated by , (level of significance) n Typical values are. 01, . 05, or. 10 n Is selected by the researcher at the beginning n Provides the critical value(s) of the test Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 9
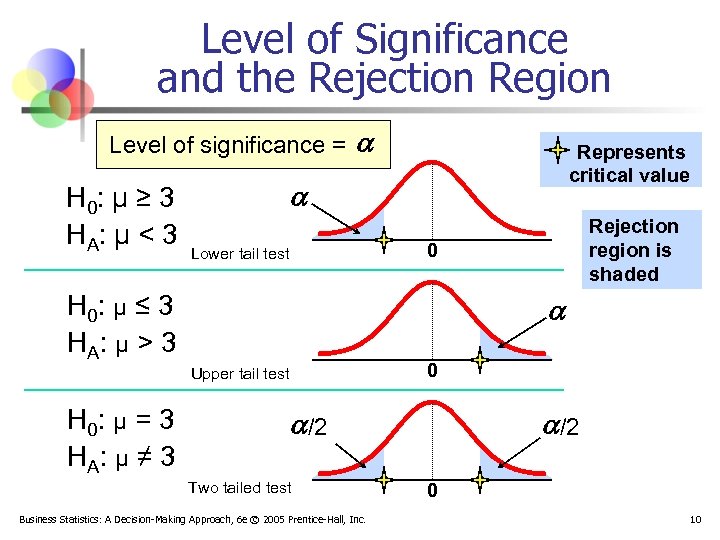
Level of Significance and the Rejection Region Level of significance = H 0: μ ≥ 3 HA : μ < 3 Rejection region is shaded 0 Lower tail test H 0: μ ≤ 3 HA : μ > 3 0 Upper tail test H 0: μ = 3 HA : μ ≠ 3 Represents critical value /2 Two tailed test Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. /2 0 10

Errors in Making Decisions n Type I Error n Reject a true null hypothesis n Considered a serious type of error The probability of Type I Error is n Called level of significance of the test n Set by researcher in advance Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 11

Errors in Making Decisions (continued) n Type II Error n Fail to reject a false null hypothesis The probability of Type II Error is β Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 12

Outcomes and Probabilities Possible Hypothesis Test Outcomes State of Nature Decision Key: Outcome (Probability) H 0 True Do Not Reject H 0 No error (1 - ) Type II Error (β) Reject H 0 Type I Error ( ) No Error (1 -β) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. H 0 False 13

Type I & II Error Relationship § Type I and Type II errors can not happen at the same time § Type I error can only occur if H 0 is true § Type II error can only occur if H 0 is false If Type I error probability ( ) , then Type II error probability ( β ) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 14

Factors Affecting Type II Error n All else equal, n β when the difference between hypothesized parameter and its true value n β when σ n β when n Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 15

Critical Value Approach to Testing n n n Convert sample statistic (e. g. : statistic ( Z or t statistic ) ) to test Determine the critical value(s) for a specified level of significance from a table or computer If the test statistic falls in the rejection region, reject H 0 ; otherwise do not reject H 0 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 16
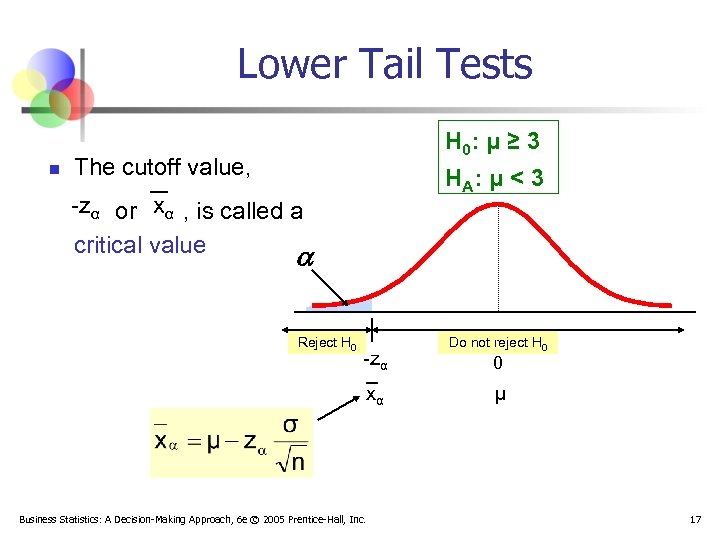
Lower Tail Tests n H 0: μ ≥ 3 The cutoff value, H A: μ < 3 -zα or xα , is called a critical value Reject H 0 -zα xα Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Do not reject H 0 0 μ 17
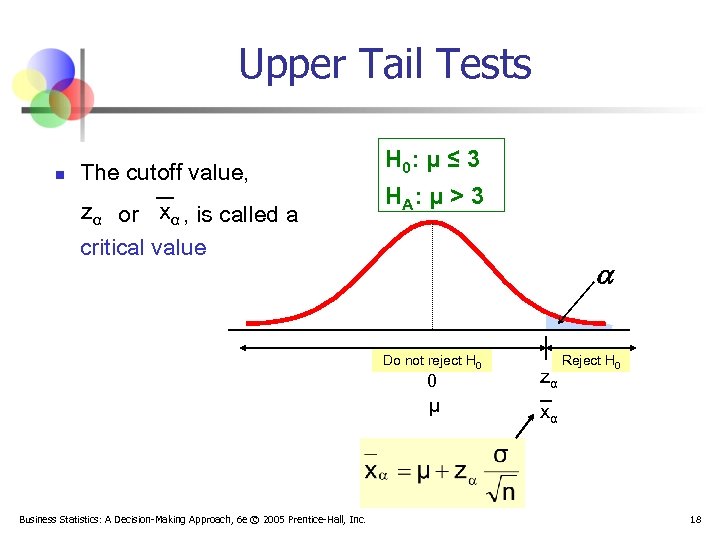
Upper Tail Tests n The cutoff value, zα or xα , is called a critical value H 0: μ ≤ 3 H A: μ > 3 Do not reject H 0 0 μ Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. zα Reject H 0 xα 18
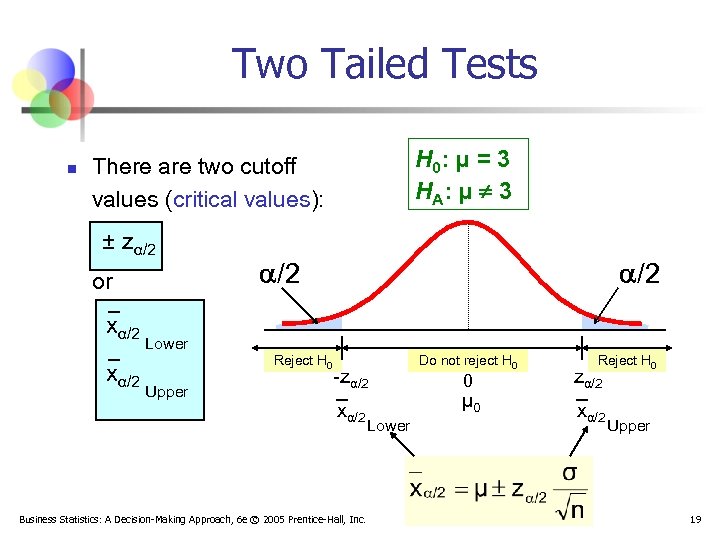
Two Tailed Tests n H 0: μ = 3 H A: μ ¹ 3 There are two cutoff values (critical values): ± zα/2 or xα/2 /2 Lower Reject H 0 Upper -zα/2 xα/2 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Lower Do not reject H 0 0 μ 0 Reject H 0 zα/2 xα/2 Upper 19

Critical Value Approach to Testing n Convert sample statistic ( x ) to a test statistic ( Z or t statistic ) Hypothesis Tests for Known Unknown Large Samples Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Small Samples 20
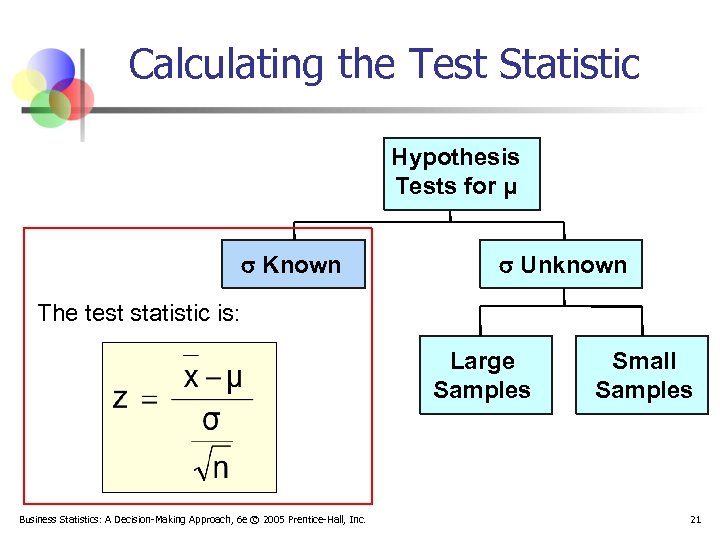
Calculating the Test Statistic Hypothesis Tests for μ Known Unknown The test statistic is: Large Samples Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Small Samples 21

Calculating the Test Statistic (continued) Hypothesis Tests for Known The test statistic is: But is sometimes approximated using a z: Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. Unknown Large Samples Small Samples 22

Calculating the Test Statistic (continued) Hypothesis Tests for Known Unknown The test statistic is: Large Samples Small Samples (The population must be approximately normal) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 23

Review: Steps in Hypothesis Testing n n 1. Specify the population value of interest 2. Formulate the appropriate null and alternative hypotheses n 3. Specify the desired level of significance n 4. Determine the rejection region n n 5. Obtain sample evidence and compute the test statistic 6. Reach a decision and interpret the result Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 24

Hypothesis Testing Example Test the claim that the true mean # of TV sets in US homes is at least 3. (Assume σ = 0. 8) n n n 1. Specify the population value of interest n The mean number of TVs in US homes 2. Formulate the appropriate null and alternative hypotheses n H 0: μ 3 HA: μ < 3 (This is a lower tail test) 3. Specify the desired level of significance n Suppose that =. 05 is chosen for this test Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 25
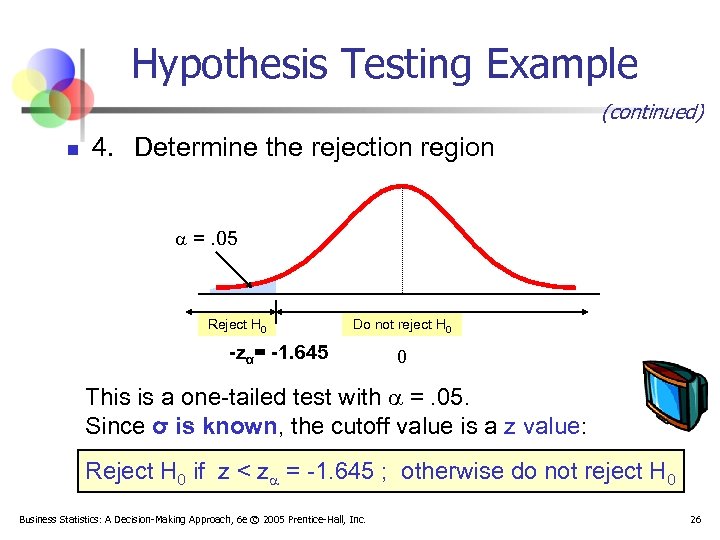
Hypothesis Testing Example (continued) n 4. Determine the rejection region =. 05 Reject H 0 Do not reject H 0 -zα= -1. 645 0 This is a one-tailed test with =. 05. Since σ is known, the cutoff value is a z value: Reject H 0 if z < z = -1. 645 ; otherwise do not reject H 0 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 26

Hypothesis Testing Example n 5. Obtain sample evidence and compute the test statistic Suppose a sample is taken with the following results: n = 100, x = 2. 84 ( = 0. 8 is assumed known) n Then the test statistic is: Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 27
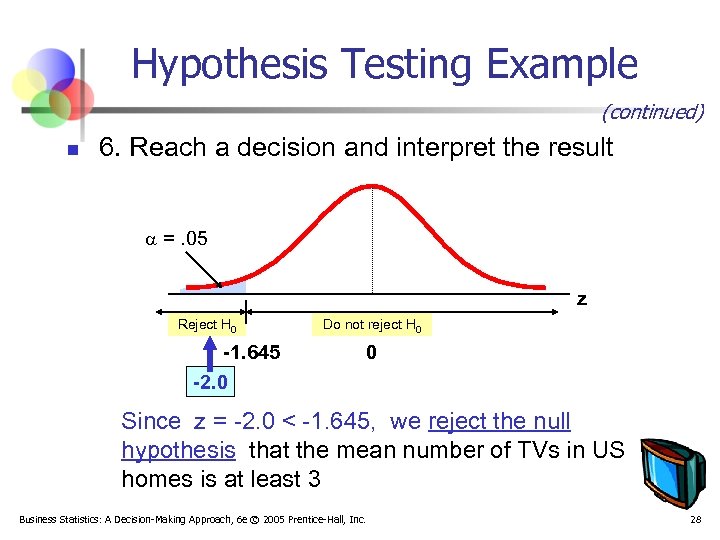
Hypothesis Testing Example (continued) n 6. Reach a decision and interpret the result =. 05 z Reject H 0 -1. 645 -2. 0 Do not reject H 0 0 Since z = -2. 0 < -1. 645, we reject the null hypothesis that the mean number of TVs in US homes is at least 3 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 28
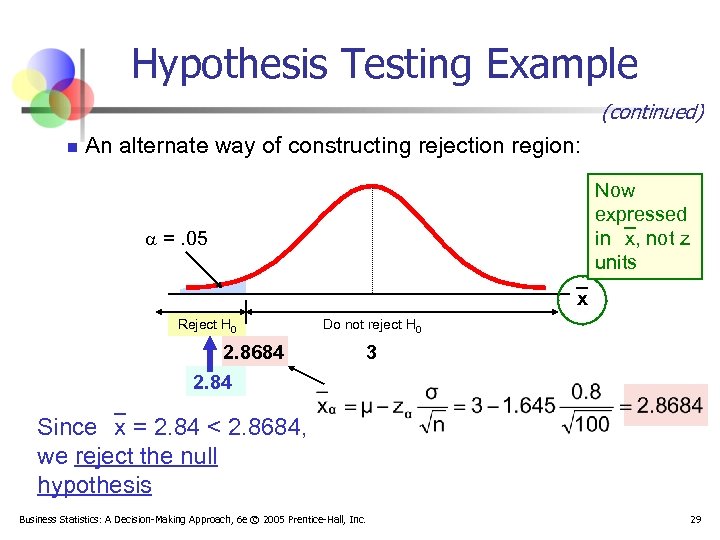
Hypothesis Testing Example (continued) n An alternate way of constructing rejection region: Now expressed in x, not z units =. 05 x Reject H 0 2. 8684 2. 84 Do not reject H 0 3 Since x = 2. 84 < 2. 8684, we reject the null hypothesis Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 29

p-Value Approach to Testing n Convert Sample Statistic (e. g. x ) to Test Statistic ( Z or t statistic ) n Obtain the p-value from a table or computer n Compare the p-value with n If p-value < , reject H 0 n If p-value , do not reject H 0 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 30

p-Value Approach to Testing (continued) n p-value: Probability of obtaining a test statistic more extreme ( ≤ or ) than the observed sample value given H 0 is true n n Also called observed level of significance Smallest value of for which H 0 can be rejected Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 31
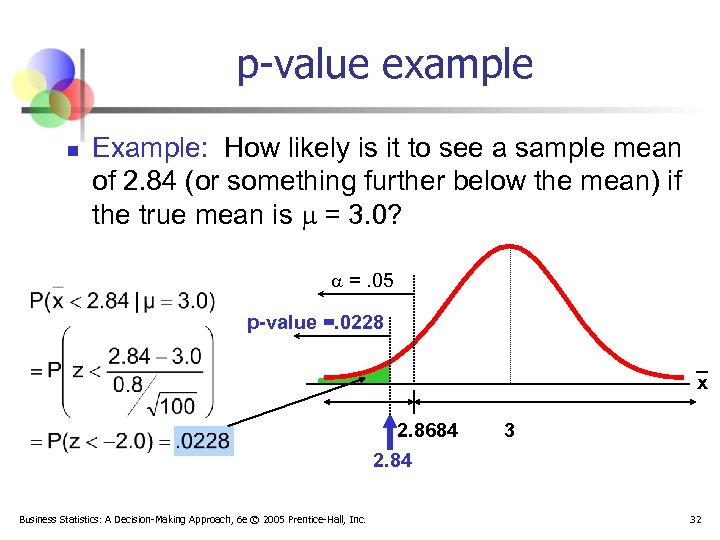
p-value example n Example: How likely is it to see a sample mean of 2. 84 (or something further below the mean) if the true mean is = 3. 0? =. 05 p-value =. 0228 x 2. 8684 2. 84 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 3 32

p-value example (continued) n Compare the p-value with n If p-value < , reject H 0 n If p-value , do not reject H 0 =. 05 Here: p-value =. 0228 =. 05 Since. 0228 <. 05, we reject the null hypothesis p-value =. 0228 2. 8684 3 2. 84 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 33

Example: Upper Tail z Test for Mean ( Known) A phone industry manager thinks that customer monthly cell phone bill have increased, and now average over $52 per month. The company wishes to test this claim. (Assume = 10 is known) Form hypothesis test: H 0: μ ≤ 52 the average is not over $52 per month HA: μ > 52 the average is greater than $52 per month (i. e. , sufficient evidence exists to support the manager’s claim) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 34

Example: Find Rejection Region (continued) n Suppose that =. 10 is chosen for this test Find the rejection region: Reject H 0 =. 10 Do not reject H 0 0 zα=1. 28 Reject H 0 if z > 1. 28 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 35
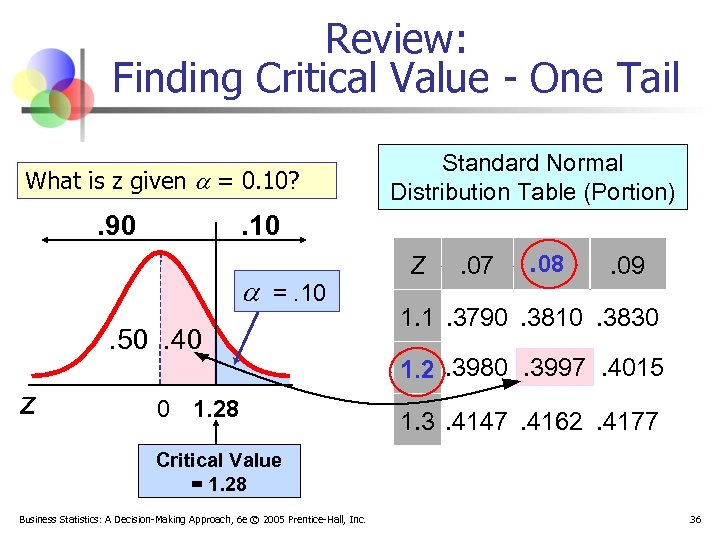
Review: Finding Critical Value - One Tail What is z given a = 0. 10? . 90 . 10 a =. 10. 50. 40 z Standard Normal Distribution Table (Portion) 0 1. 28 Z . 07 . 08 . 09 1. 1. 3790. 3810. 3830 1. 2. 3980. 3997. 4015 1. 3. 4147. 4162. 4177 Critical Value = 1. 28 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 36

Example: Test Statistic (continued) Obtain sample evidence and compute the test statistic Suppose a sample is taken with the following results: n = 64, x = 53. 1 ( =10 was assumed known) n Then the test statistic is: Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 37
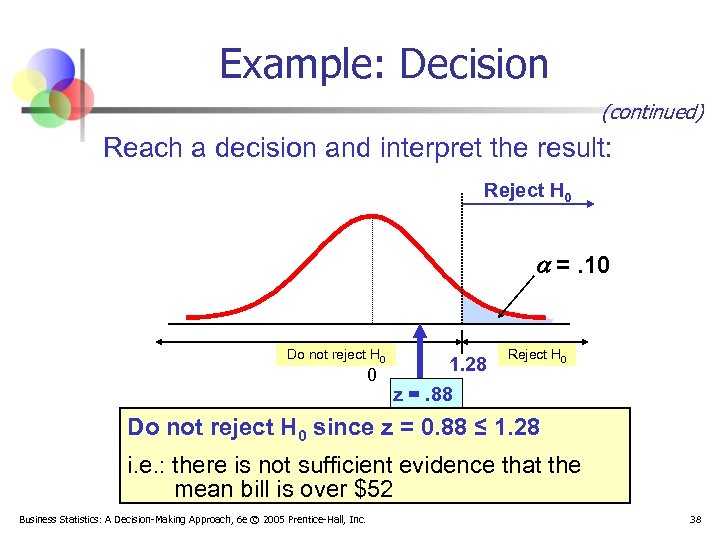
Example: Decision (continued) Reach a decision and interpret the result: Reject H 0 =. 10 Do not reject H 0 1. 28 0 z =. 88 Reject H 0 Do not reject H 0 since z = 0. 88 ≤ 1. 28 i. e. : there is not sufficient evidence that the mean bill is over $52 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 38
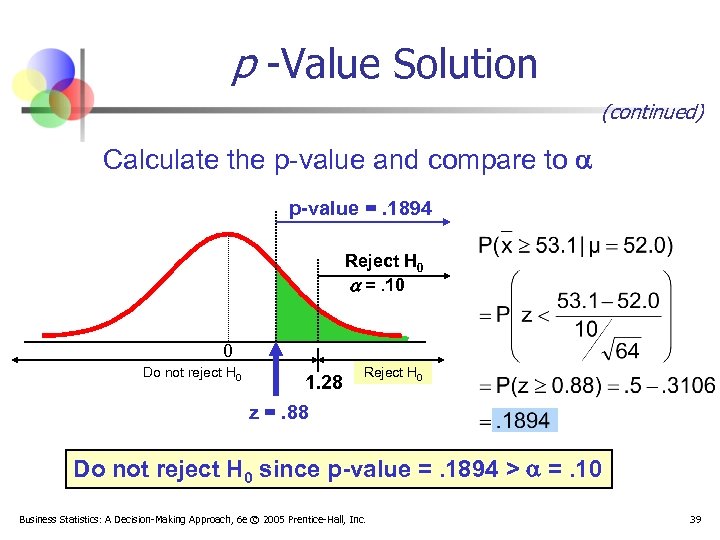
p -Value Solution (continued) Calculate the p-value and compare to p-value =. 1894 Reject H 0 =. 10 0 Do not reject H 0 1. 28 z =. 88 Reject H 0 Do not reject H 0 since p-value =. 1894 > =. 10 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 39

Example: Two-Tail Test ( Unknown) The average cost of a hotel room in New York is said to be $168 per night. A random sample of 25 hotels resulted in x = $172. 50 and s = $15. 40. Test at the = 0. 05 level. H 0: μ = 168 HA: μ ¹ 168 (Assume the population distribution is normal) Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 40
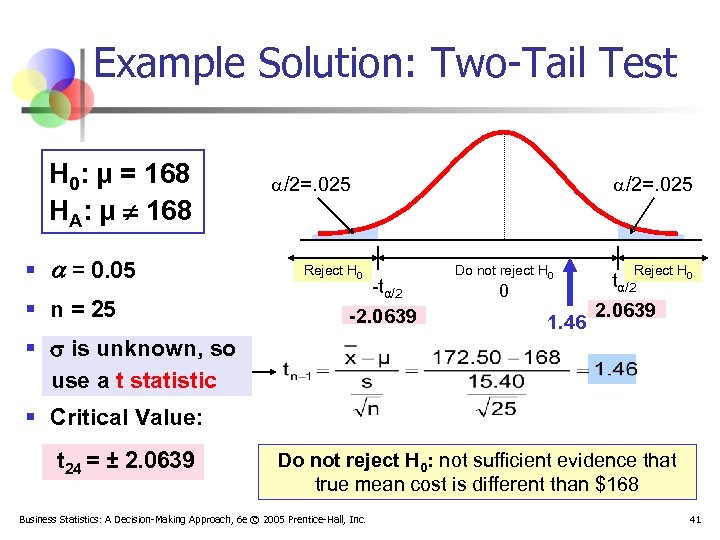
Example Solution: Two-Tail Test H 0: μ = 168 HA: μ ¹ 168 § = 0. 05 § n = 25 /2=. 025 Reject H 0 -tα/2 -2. 0639 § is unknown, so use a t statistic /2=. 025 Do not reject H 0 0 1. 46 Reject H 0 tα/2 2. 0639 § Critical Value: t 24 = ± 2. 0639 Do not reject H 0: not sufficient evidence that true mean cost is different than $168 Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 41

Chapter Summary n Addressed hypothesis testing methodology n Performed z Test for the mean (σ known) n Discussed p–value approach to hypothesis testing n Performed one-tail and two-tail tests. . . n Performed t test for the mean (σ unknown) n Discussed type II error and computed its probability Business Statistics: A Decision-Making Approach, 6 e © 2005 Prentice-Hall, Inc. 42
d535d328f2f37c6d928438cf010d8adb.ppt