L1_2.pptx
- Количество слайдов: 23

БУЛЕВЫ ФУНКЦИИ Булевыми функциями принято называть такие функции у которых все аргументы, как и сами функции могут принимать лишь два различных значения. Булева функция (от n переменных) — это произвольное отображение вида f: {0, 1}n {0, 1})
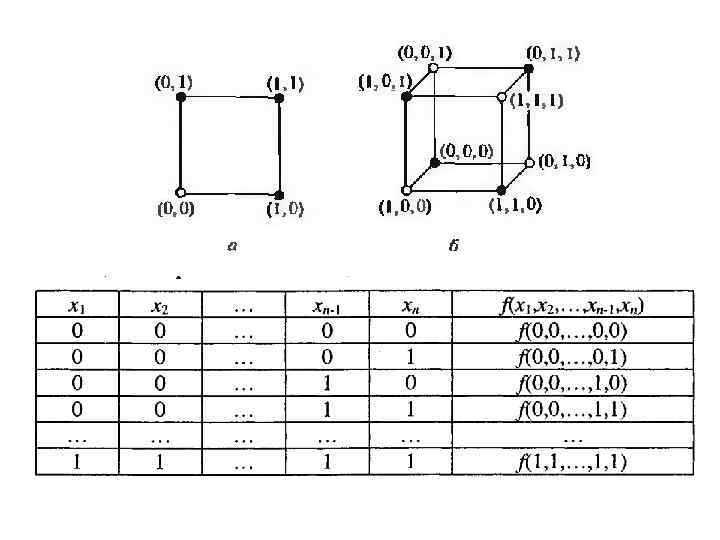

Булевы функции от n переменных называются равными, если они принимают одинаковые значения на соответствующих одинаковых наборах переменных, в них входящих. Равные функции реализуются равносильными формулами. Равносильность формул доказывается: 1. С помощью таблиц истинности 2. Методом эквивалентных преобразований. 3. На основе применения принципа двойственности

Суперпозицией булевых функций f 0 и f 1, . . . , fn называется функция f(x 1, . . . , xm) = f 0(g 1(x 1, . . . , xm), . . . , gk(x 1, . . . , xm)), где каждая из функций gi(x 1, . . . , xm) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f 1, . . . , fn. Пример (суперпозиция функций): Функция f(x, y) = ¬(x & y) является суперпозицией функций ¬ и &. Функция g(x, y) = x (x y) является суперпозицией функций и . Функция h(x, y, z) = (x & y) z является суперпозицией функций и &. Функция g(x 1, . . . , xn) = ¬f(¬x 1, . . . , ¬xn) называется двойственной функцией к функции f и обозначается f*. Пример (двойственные функции): (x & y)* = ¬(¬x & ¬y) = x y. Принцип двойственности. Если формула F=F(f 1, …, fm) реализует функцию ϕ(x 1, …, xn), то формула F*=F(f 1*, …, fm*) полученная из F заменой функций f 1, …, fm на f 1*, …, fm*, реализует функцию ϕ*(x 1, …, xn).

Практика

Некоторые эквивалентности: 1) x y = (x y) y; 2) x ~ y = (x y) & (y x); 3) x y: =((x|x)|(y|y))|((x|x)|(y|y)); 4) x (y ~ z) = (x y)~(x z); 5) x & (y ~ z) = ((x & y) ~ (x & z)) ~ x; 6) x (y ~ z) = (x y) ~ (x z); 7) x (y z) = (x y) (x z); 8) x & (y z) = (x y) (x & z); 9) x (y V z) = (x y) V (x z); 10) x (y & z) = (x y) & (x z); 11) x (y z) = (x y) (x z).

Эквивалентности алгебры логики 1. x y = y x - коммутативность для , , , | 2. (x y) z = x (y z) – ассоциативность для , , , 3. a)x & (y Z) = (x & y) (x & z) - дистрибутивность конъюнкции относительно дизъюнкции б) x (y & z) — (x y) & (x z) – дистрибутивность дизъюнкции относительно конъюнкции в) x & (y Z) = (X & y) (x & Z) - дистрибутивность конъюнкции относительно сложения по модулю 2 4. a) (x & y) = x y; б) (x y) = x & y (правило Де Моргана), 5. a) x (x & y) = x; 6) x & (x V y) = x (правила поглощения). 6. a) x ( x&y) =x y; 6) x&( x y) = x&y. 7. a)x& x = x&0 = x x = 0; закон противоречия 6)x x = x l = x~x = x x = l; Закон исключенного третьего в)x x = x&l = x 0 = x; Закон идемпотентности г)x l = x 0 = x~0 = x|x = x; д) x = x. Закон двойного отрицания 8. a) x y = (x& y) ( x&y) = (x y) &( x y); 6) x~y = (x y) = (x&y) ( x& y) = (x y)&( x y); в) x y = ((x & y) x) 1. 9. a)x|y = (x&y) = x y; 6)x y = (x y)= x y.

Основные эквивалентности алгебры логики: 1. Коммутативность: x ∨ y = y ∨ x ; xy = yx ; x ⊕ y = y ⊕ x ; x ~ y = y ~ x. 3. Дистрибутивность: (x ⊕ y) z = (xz) ⊕ (yz) ; (x ∨ y) z = (xz) ∨ (yz) ; (xy) ∨ z = (x ∨ z)·(y ∨ z). 5. Законы поглощения. x ∨ x = x x · x = x x ∨ x = 1 x ⋅ x = 0 x ∨ 1 = 1 x · 1 = x x ∨ 0 = x x · 0 = 0.

Теорема о разложении функции алгебры логики по переменным Лемма (о дизъюнктивном разложении). Любая булева функция f (x 1, …, xn) от n переменных может быть представлена так: f(x 1, …, xi, …, xn) = xi * f(x 1, …, 0, …, xn) xi * f(x 1, …, xn) Теорема. Любая двоичная функция может быть представлена как суперпозиция только тр ёх функций: и, или, не. f(p, q, r) = p q rq(p r) = p q r p qr pq r Определение. Функционально полным набором (или базисом) будем называть такое множество двоичных функций , суперпозицией которых могут быть выражены любые булевы функции. Очевидно, что множество булевых функций {И, ИЛИ, НЕ} является базисом. Базис {И, ИЛИ, НЕ} называется базисом Буля.

Нормальные формы представления булевых функций Определение. Представление булевой функции в форме дизъюнкции: f(x 1, …, xi, …, xn) = K 1, K 2 , …, Km, m>=1, где каждый терм Ki (или конъюнкт) представляет собой конъюнкцию взятых с отрицанием или без них двоичных переменных функции, называется дизъюнктивной нормальной формой этой функции (или ДНФ). Если каждый конъюнкт содержит в точности по одной все (взятые с отрицаниями или без них) двоичные переменные функции, ДНФ называется совершенной дизъюнктивной нормальной формой этой функции или СДНФ. Примеры ДНФ: F(p, q, r) = p q r p qr pq r – СДНФ F(p, q, r) = p r q r p q pq r p q r F(p, q, r) = p r q r p q

Определение. Представление булевой функции в форме конъюнкции: f(x 1, …, xi, …, xn) = D 1 D 2 … Dm, m>=1, где каждый терм Di (или дизъюнкт) представляет собой дизъюнкцию взятых с отрицанием или без них двоичных переменных функции, называется конъюнктивной нормальной формой этой функции (или КНФ). Если каждый дизъюнкт содержит в точности по одной все (взятые с отрицаниями или без них) двоичные переменные функции, КНФ называется совершенной конъюнктивной нормальной формой этой функции или СКНФ. Лемма. Любая булева функция f (x 1, …, xi, …, xn) от n переменных может быть представлена так: f(x 1, …, xi, …, xn) = ( xi f(x 1, …, 0, …, xn)) * (xi f(x 1, …, xn) )

Преобразование в нормальную форму

Следующим этапом в исследовании эквивалентных формул будет получение функций равных исходной, записанных меньшим числом знаков.

Минимизация булевых функций Общая задача минимизации – найти аналитическое представление БФ, содержащей минимальное число букв. Определение. Всякое произведение (дизъюнкция) переменных, взятых с отрицанием или без называется элементарным произведением (дизъюнкцией), если в нём (ней) каждая буква встречается не более одного раза. Определение. ДНФ (КНФ) – это дизъюнкция (произведение) элементарных произведений (дизъюнкций) Определение. Элементарные произведения (дизъюнкции) максимальной длины, называются конституэнтами единицы (нуля). Пример: (x 1) * ( x 2) * ( x 3) * ( x 4) (x 1) ( x 2) ( x 3) ( x 4) Определение: ДНФ (КНФ) состоящая исключительно из конституэнт 1 (0) – СДНФ (СКНФ). На практике часто ограничиваются задачей нахождения минимальной формулы в классе дизъюнктивных нормальных форм.

Определение. Минимальное ДНФ – это ДНФ, содержащая наименьшее число букв, по отношению ко всем другим ДНФ, представляющим заданную функцию. Определение. Импликантой булевой функции f называют всякую булеву функцию g, обращение которой в единицу возможно лишь на тех наборах значений переменных, на которых обращается в единицу функция f. Говорят, что импликанта g накрывает своими единицами некоторые единицы функции f. Дизъюнкция любого множества импликант g 1, g 2, …, gn функции f снова будет импликантой. Если при этом единицы импликант g 1, g 2, …, gn функции f накрывают все её единицы, то эта дизъюнкция просто совпадает с функцией f. F: g 1 g 2 … gn = f Для упрощения БФ используются законы склеивания и поглощения. Закон поглощения x ∨ x*y = x x*(x ∨ y) = x Закон склеивания A*x ∨ A* x = A Пример: x*y ∨ x*y = y

Определение. Импликанта g булевой функции f, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты g не является импликантой функции f. x 1 x 2 x 3 f g 1 g 2 g 3 g 4 g 5 g 6 g 7 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 1 1 1 0 1 0 1 СДНФ: F = x 1 x 2 x 3 x 1 x 2 x 3 g 6 = x 1 x 2 x 3 x 1 x 2 x 3 g 5 = x 1 x 2 x 3 = x 2 x 3 – простая g 4 = x 1 x 2 x 3 g 3 = x 1 x 2 x 3 x 1 x 2 x 3 = x 1 x 2 – простая g 2 = x 1 x 2 x 3 Импликанты g 1, g 2, g 4, g 6 не являются простыми, так как их части являются импликантами функции f, например g 3 является частью g 1

Дизъюнкция любого числа импликант булевой функции f также является импликантой этой функции. Любая булева функция f эквивалентна дизъюнкции всех своих простых импликант. Такая форма представления булевой функции называется сокращенной ДНФ. Иногда из сокращенной ДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты назовем лишними. Исключение лишних простых импликант из сокращенных ДНФ - второй этап минимизации. Определение. Сокращенная ДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты. Устранение лишних простых импликант из сокращенной ДНФ булевой функции не является однозначным процессом, т. е. булева функция может иметь несколько тупиковых ДНФ.
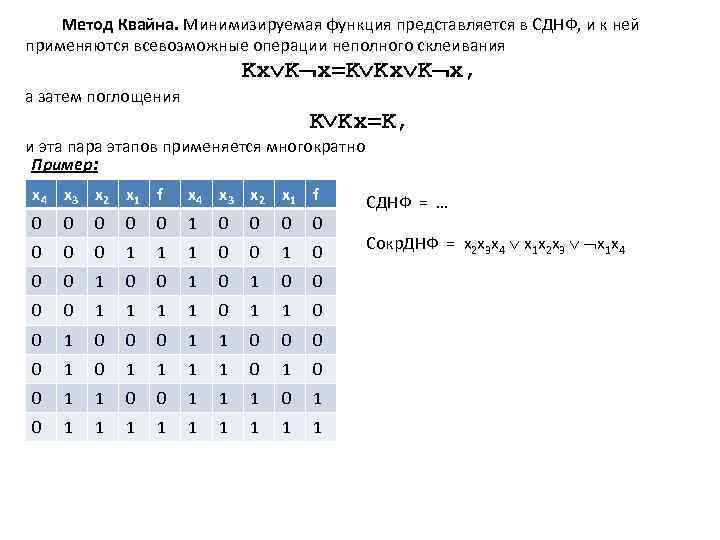
Метод Квайна. Минимизируемая функция представляется в СДНФ, и к ней применяются всевозможные операции неполного склеивания Kx K x=K Kx K x, а затем поглощения K Kx=K, и эта пара этапов применяется многократно Пример: x 4 x 3 x 2 x 1 f 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 1 1 1 СДНФ = … Сокр. ДНФ = x 2 x 3 x 4 x 1 x 2 x 3 x 1 x 4
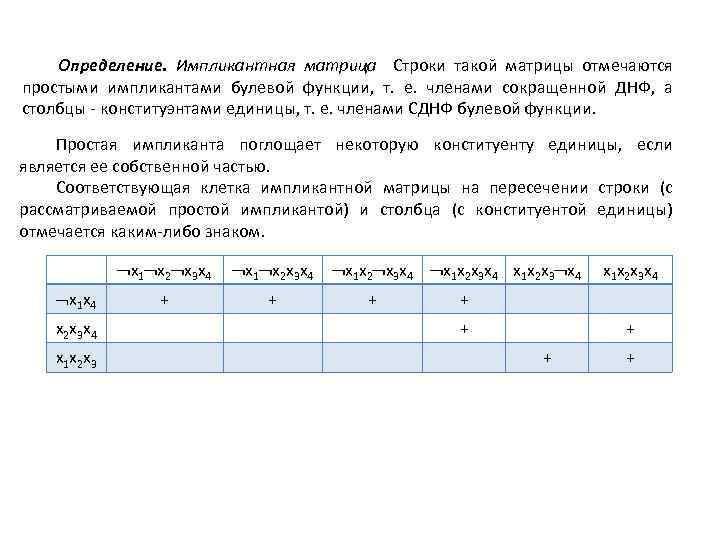
Определение. Импликантная матрица Строки такой матрицы отмечаются простыми импликантами булевой функции, т. е. членами сокращенной ДНФ, а столбцы - конституэнтами единицы, т. е. членами СДНФ булевой функции. Простая импликанта поглощает некоторую конституенту единицы, если является ее собственной частью. Соответствующая клетка импликантной матрицы на пересечении строки (с рассматриваемой простой импликантой) и столбца (с конституентой единицы) отмечается каким-либо знаком. x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 1 x 4 x 2 x 3 x 4 x 1 x 2 x 3 + + x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 + x 1 x 2 x 3 x 4 + + +

Минимальные ДНФ строятся по импликантной матрице следующим образом: • ищутся столбцы импликантной матрицы, имеющие только одну отметку. Соответствующие этим отметмка простые импликанты называются базисными и составляют так называемое ядро булевой функции. Ядро обязательно входит в минимальную ДНФ. • рассматриваются различные варианты выбора совокупности простых импликант, которые накроют отметмками остальные столбцы импликантной матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант. Ядро: x 1 x 2 x 3 ; x 1 x 4 Импликанта x 2 x 3 x 4 лишняя, так как ядро накрывает все столбцы импликантной матрицы Тупиковая ДНФ: x 1 x 2 x 3 x 1 x 4 Следует отметить, что число N отметок в одной строке всегда является степенью 2. Более того, читатель может легко убедиться в том, что N = 2 n-k , где k – число букв, содержащихся в простой импликанте. Метод Блейка AB AC = AB AC BC Результат Блейка состоит в том, что преобразуемая форма f будет содержать все простые импликанты представляемой ею булевой функции
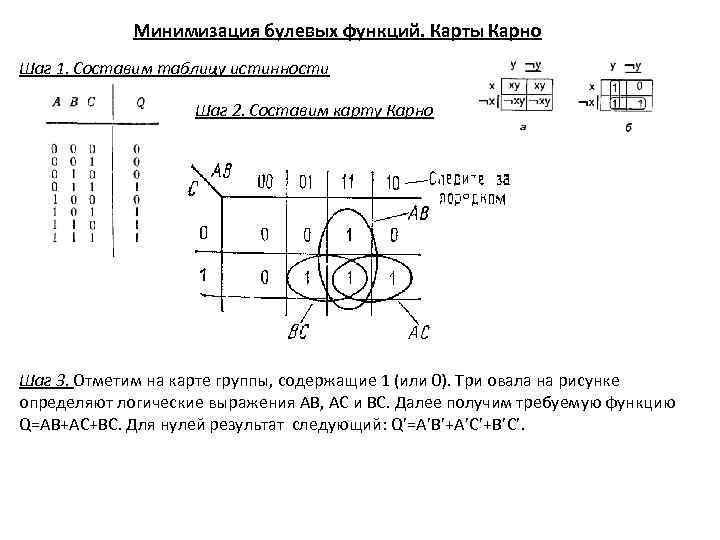
Минимизация булевых функций. Карты Карно Шаг 1. Составим таблицу истинности Шаг 2. Составим карту Карно Шаг 3. Отметим на карте группы, содержащие 1 (или 0). Три овала на рисунке определяют логические выражения AB, AC и BC. Далее получим требуемую функцию Q=AB+AC+BC. Для нулей результат следующий: Q’=A’B’+A’C’+B’C’.


Принцип построения карты Карно на примере ДНФ: 1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала 2 n (n - целое число = 0, 1, …) клеток. Помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули; 2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки); Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат. 3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну; 4. Область должна быть как можно больше, а количество областей как можно меньше; 5. Области могут пересекаться; 6. Возможно несколько вариантов покрытия.
L1_2.pptx