Цифровые логические элементы+++!!!.ppt
- Количество слайдов: 43

Булева алгебра. ФАЛ. Цифровые логические элементы. Булева алгебра. Базовые логические элементы И, ИЛИ, НЕ, M 2 Функции алгебры логики Законы Булевой алгебры.

Введение Математической основой цифровой электроники и вычислительной техники является алгебра логики или булева алгебра (по имени английского математика Джорджа Буля (1815 -1864 гг. )). В булевой алгебре независимые переменные или аргументы (X) принимают только два значения: 0 или 1. Зависимые переменные или функции (Y) также могут принимать только одно из двух значений: 0 или 1. Функция алгебры логики представляется в виде: Y = F (X 1; X 2; X 3. . . XN ).

Введение • Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений: ложь или истина (их можно обозначать как 0 и 1, F и T, false и true). • (Для сравнения, элементарная алгебра занимается арифметическими выражениями и операциями. ) • Булева алгебра получила свое название в честь своего создателя Джорджа Буля (1854 г. ), являющегося одним из основателей математической логики. • Среди своих прочих приложений, булева алгебра позволяет программистам формулировать сложные условия для применения в условных операторах или операторах цикла, а компьютерам — определять их истинность или ложность, вычисляя соответствующую информацию на основе определенных правил.

Введение Основные работы: • «Математический анализ логики» (1847); • «Логическое исчисление» (1848); • «Исследование законов мышления» (1854). • Джордж Буль (1854 г. ) 1815 - 1864

Введение • Логические операции булевой алгебры подобны арифметическим операциям элементарной алгебры. Если последние применяются к числам, то первые — к логическим значениям соответствующих высказываний. Составные высказывания можно получать с помощью логических операций так же, как в элементарной алгебре — формулы. И, если известны значения исходных высказываний, значение составного высказывания можно вычислить, прибегая лишь к вычислить формальным правилам. Уравнения, составленные в алгебре логики можно формально решать. • Все это обеспечивает широкие возможности по применению математического аппарата к суждениям из реальной жизни

Основными логическими операциями являются: • логическое отрицание (инверсия) Y = X′ = ~X = !X • логическое сложение (дизъюнкция) Y = X 1 + X 2 или Y = X 1 V X 2 • логическое умножение (конъюнкция) Y = X 1 X 2 или Y = X 1 X 2

К более сложным функциям алгебры логики относятся: • функция равнозначности (эквивалентности) Y = X 1 X 2 + X′ 1 X′ 2 или Y = X 1 ~ X 2 • функция неравнозначности (сложение по модулю два) Y = X 1 X′ 2 + X′ 1 X 2 или Y = X 1 X 2 • функция Пирса (логическое сложение с отрицанием) Y = ( X 1 + X 2 )′ • функция Шеффера (логическое умножение с отрицанием) Y = ( X 1 X 2 )′

Понятие функциональной полноты набора логических элементов:
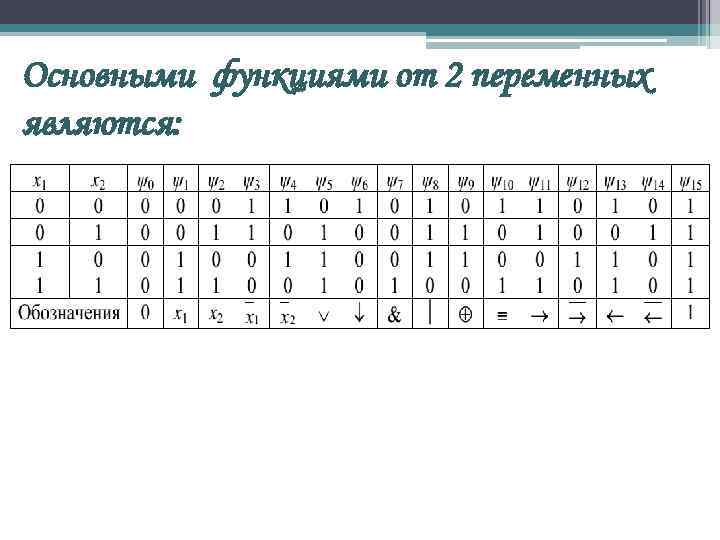
Основными функциями от 2 переменных являются:

Основными функциями от 2 переменных являются:

Основные законы БА: 4. Идемпотентность (правило повторения) а) x*x=x б) x+x=x

Основные правила БА:

Основные формы представления БА: В Булевой алгебре (высказываний) существуют две нормальные формы: конъюнктивная нормальная форма (КНФ) и дизъюнктивная нормальная форма (ДНФ). КНФ – это конъюнкция конечного числа дизъюнкций нескольких переменных или их отрицаний (произведение сумм). Например, формула X(Y + Z) находится в КНФ. ДНФ – это дизъюнкция конечного числа конъюнкций нескольких переменных или их отрицаний (сумма произведений). Например, формула X + YZ находится в ДНФ.
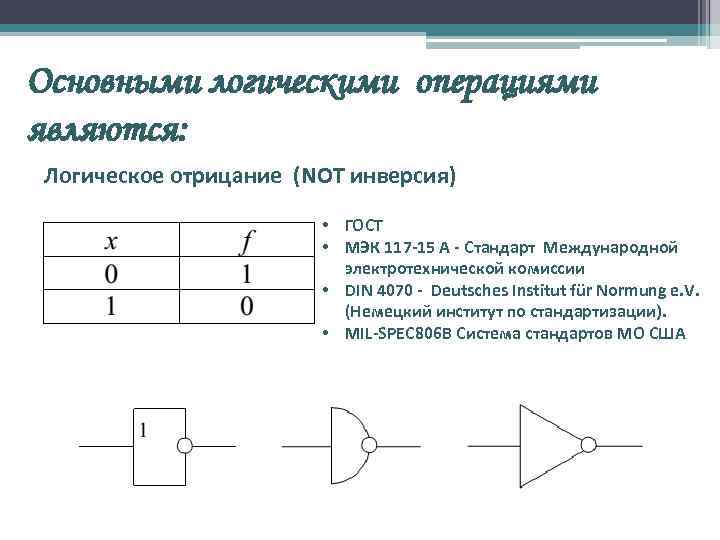
Основными логическими операциями являются: Логическое отрицание (NOT инверсия) • ГОСТ • МЭК 117 -15 A - Стандарт Международной электротехнической комиссии • DIN 4070 - Deutsches Institut für Normung e. V. (Немецкий институт по стандартизации). • MIL-SPEС 806 B Система стандартов МО США
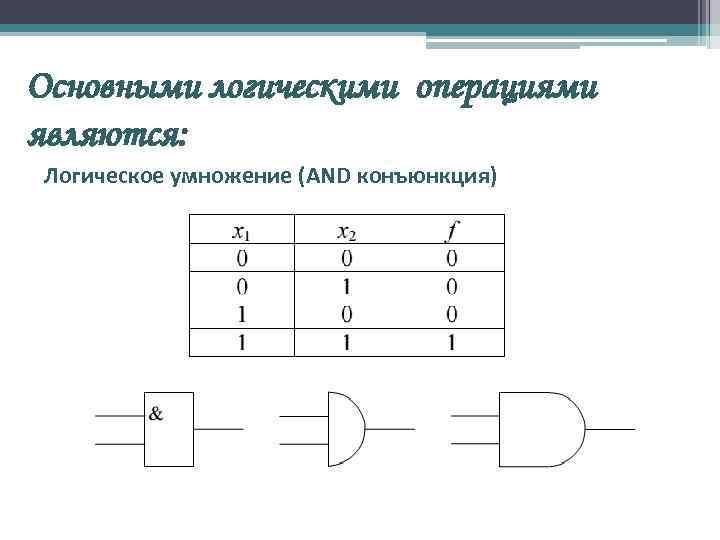
Основными логическими операциями являются: Логическое умножение (AND конъюнкция)
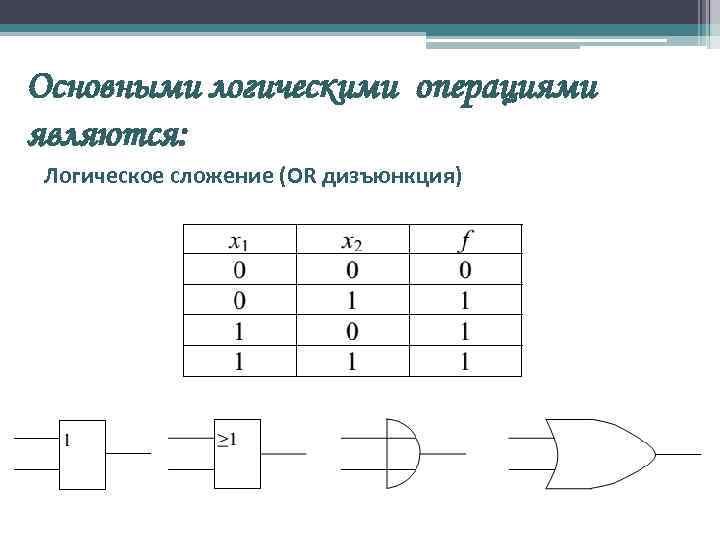
Основными логическими операциями являются: Логическое сложение (OR дизъюнкция)
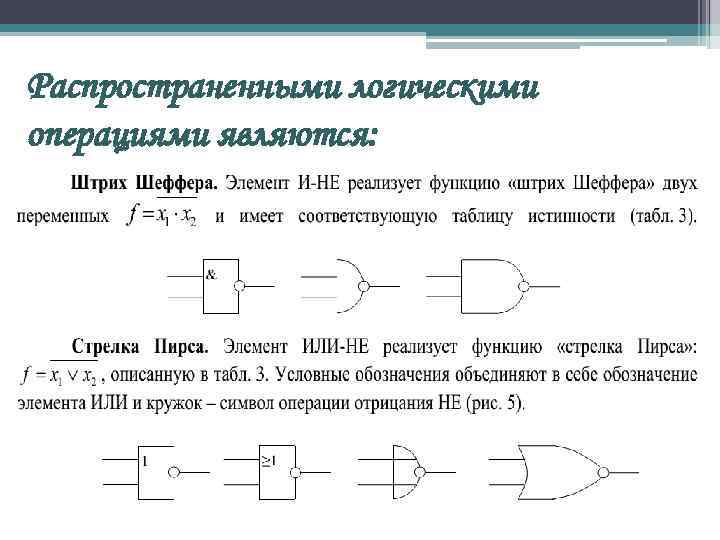
Распространенными логическими операциями являются:

Распространенными логическими операциями являются: Исключающее ИЛИ (XOR) РАВНОЗНАЧНОСТЬ

Распространенными логическими операциями являются: Сумма по модулю 2 (М 2) НЕРАВНОЗНАЧНОСТЬ 1

Распространенными логическими операциями являются: НЕЭКВИВАЛЕНТНОСТЬ НЕРАВНОЗНАЧНОСТЬ
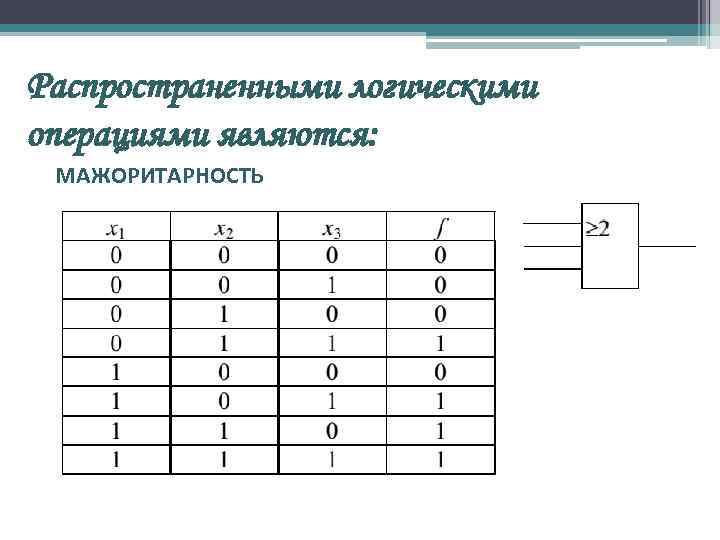
Распространенными логическими операциями являются: МАЖОРИТАРНОСТЬ

Логический элемент – это электронное устройство, реализующее одну из логических операций. Логические элементы представляют собой электронные устройства, в которых обрабатываемая информация закодирована в виде двоичных чисел, отображаемых напряжением (сигналом) высокого и низкого уровня. Логические функции – функции от двоичных переменных, которые могут принимать только одно значение: 1 или 0. Устройства, реализующие логические функции, называются цифровыми устройствами.

Условное графическое изображение цифрового комбинационного устройства На входы устройства подают комбинации двоичных переменных Х 1, Х 2, …, Хn, с выхода снимают комбинации двоичных переменных Y 1, Y 2, …, Ym. Выходные и входные переменные связаны между собой логической функцией λ.
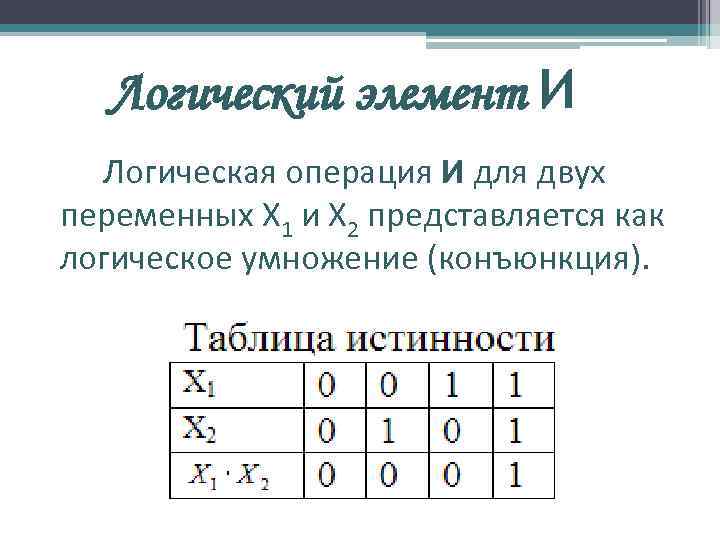
Логический элемент И Логическая операция И для двух переменных X 1 и X 2 представляется как логическое умножение (конъюнкция).
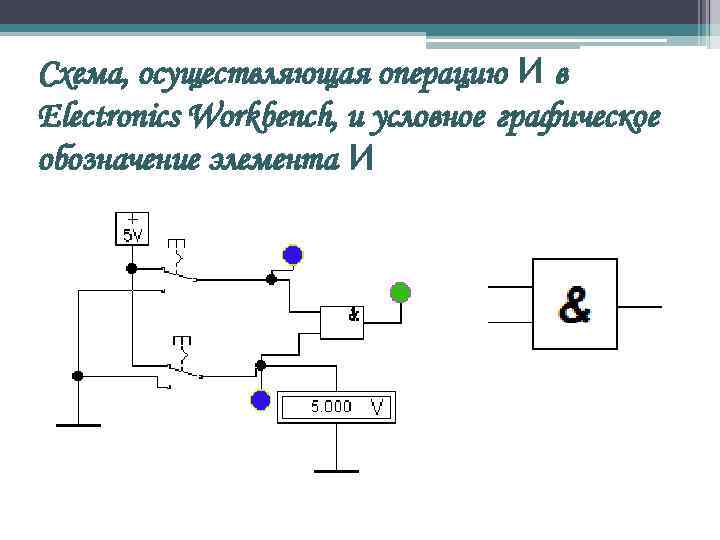
Схема, осуществляющая операцию И в Electronics Workbench, и условное графическое обозначение элемента И

Логический элемент ИЛИ Логическая операция ИЛИ для двух переменных X 1 и X 2 представляется как логическое сложение (дизъюнкция).
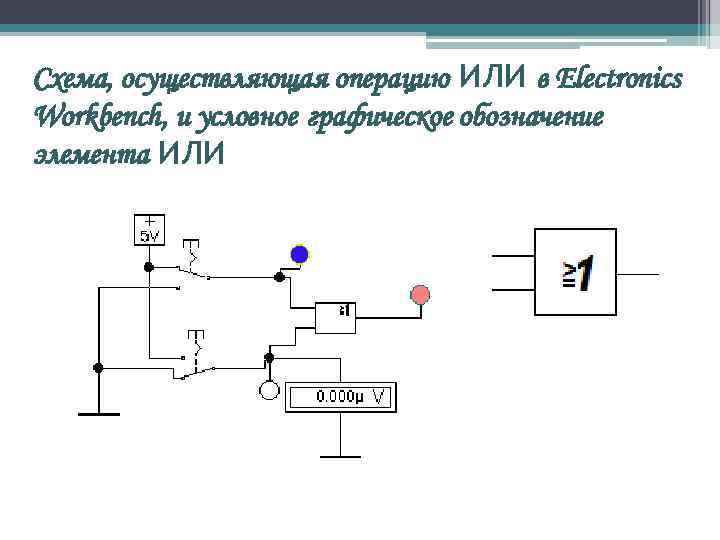
Схема, осуществляющая операцию ИЛИ в Electronics Workbench, и условное графическое обозначение элемента ИЛИ

Логический элемент НЕ Логическая операция НЕ применяется в случаях, когда требуется иметь противоположные значения переменной и представляется как логическое отрицание (инверсия).
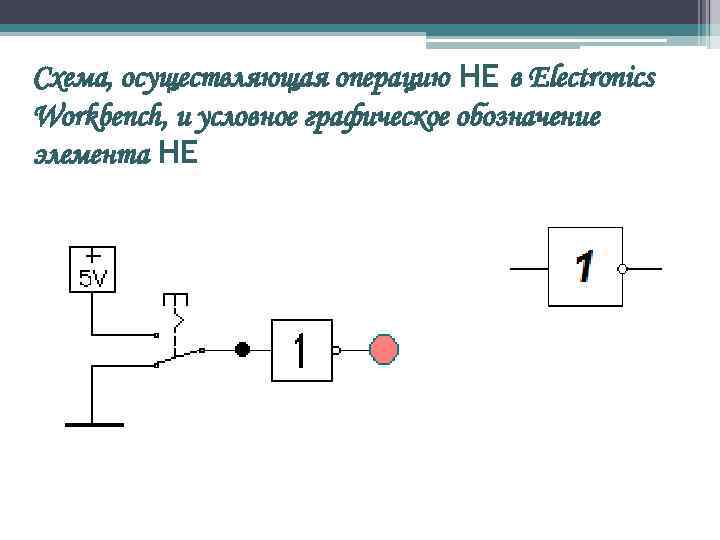
Схема, осуществляющая операцию НЕ в Electronics Workbench, и условное графическое обозначение элемента НЕ

Логический элемент И-НЕ Более универсален элемент И-НЕ, позволяющий одновременно с операцией логического умножения выполнить и отрицание, тем более что в большинстве случаев это не усложняет схемы.
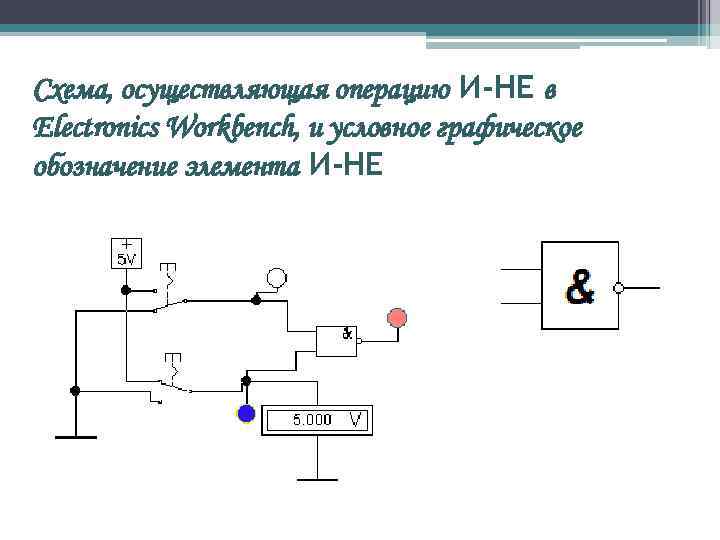
Схема, осуществляющая операцию И-НЕ в Electronics Workbench, и условное графическое обозначение элемента И-НЕ

Логический элемент ИЛИ-НЕ Более универсальный элемент ИЛИ-НЕ осуществляет одновременно с логическим сложением ИЛИ и логическое отрицание (инверсию) НЕ.
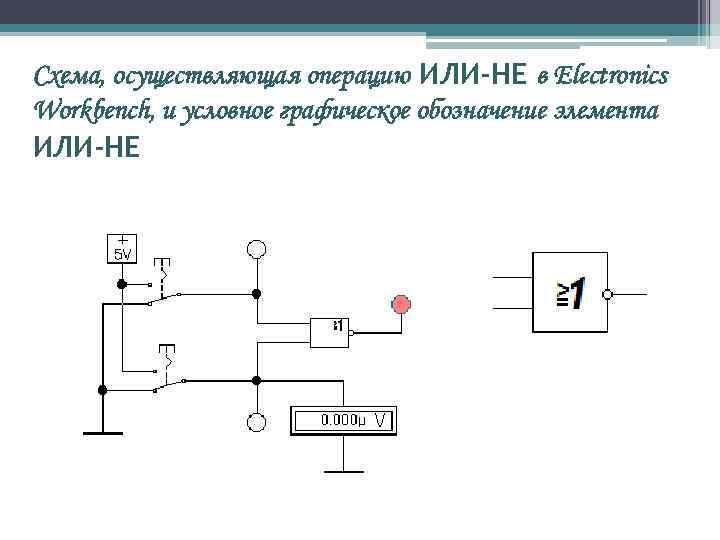
Схема, осуществляющая операцию ИЛИ-НЕ в Electronics Workbench, и условное графическое обозначение элемента ИЛИ-НЕ
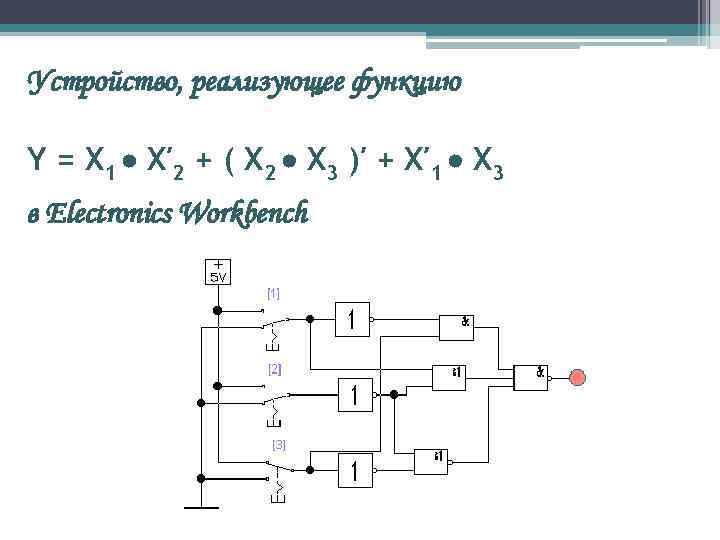
Устройство, реализующее функцию Y = X 1 X′ 2 + ( X 2 X 3 )′ + X′ 1 X 3 в Electronics Workbench
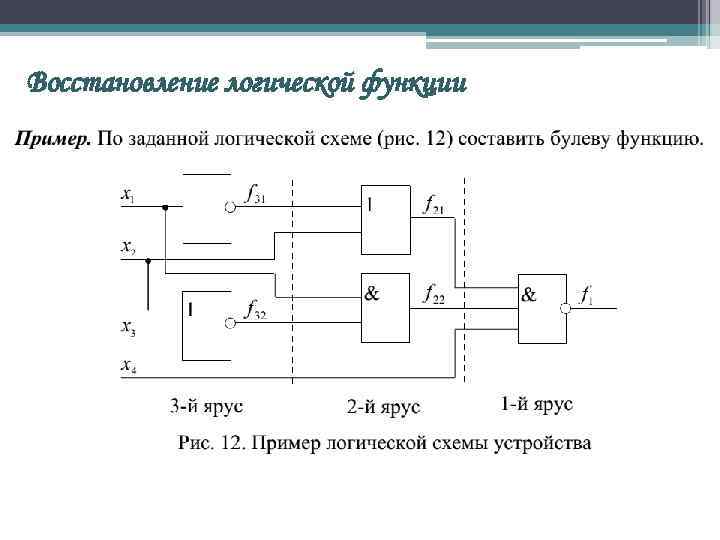
Восстановление логической функции

Восстановление логической функции Произведем

Основными логическими операциями являются: Приоритеты основных логических операций соответствуют приоритетам аналогичных операций в элементарной алгебре. Приоритеты логических операций Отрицание Конъюнкция Дизъюнкция, исключающее ИЛИ Импликация, эквивалентность

Связь между логическими операциями и множествами: Пересечение = И

Связь между логическими операциями и множествами: Объединение = ИЛИ

Связь между логическими операциями и множествами: Дополнение = НЕ

Связь между логическими операциями и множествами: Пример

Связь между логическими операциями и множествами: Пример 1 2 3 4 ~A*~C*B ~A+~C+B ~(B*A)*C B*(C+~A)

Литература 1. «Математический анализ логики» (1847); 2. «Логическое исчисление» (1848); 3. «Исследование законов мышления» (1854).
Цифровые логические элементы+++!!!.ppt